基于点集偏差的船舶交通流不均匀性度量研究*
2019-07-01胡佑希刘敬贤李欢欢
胡佑希 刘敬贤 刘 奕 李欢欢 刘 钊
(武汉理工大学航运学院1) 武汉 430063) (内河航运技术湖北省重点实验室2) 武汉 430063)
0 引 言
船舶交通流的基础理论研究多借鉴于道路、行人和航空交通领域相关理论,已取得一定成果[1].现阶段,国内外针对船舶交通流的研究主要集中在基于概率统计和模拟仿真技术的船舶行为特征分析与建模方面[2-7],同时,在船舶AIS的强制使用以及通讯技术的不断发展中,对船舶交通流的研究更多通过历史统计的船舶AIS数据进行相关研究.熊振南等[8]通过运用点统计法方法,对天津港北航道和主航道交汇水域的船舶交通流分布规律进行统计分析.甘浪雄等[9]以AIS数据为基础,引入场方法对船舶交通流密度、速度的空间分布进行表征.Pallotta等[10-11]通过对历史AIS数据的统计分析,对研究水域的船舶交通流轨迹进行特征提取以及异常检测研究.Liu等[12-13]通过结合综合考虑多因素影响的船舶交通流特性建立了其数学分析模型.现有的研究理论和方法主要通过提取船舶交通流的相关动态特性进行相关分析,区域范围内船舶交通流形态特征的度量研究尚属空白.
本研究结合了区域船舶交通流特征中的不均匀特性,将点集偏差理论运用到对区域船舶交通流形态分布特征的度量中.选取长江口水域船舶交通流作为研究对象,将船舶交通流空间分布不均匀性的度量问题表征为多维点集分布的偏差问题,旨在提出一种区域船舶交通空间分布不均匀性合理度量方法以及定量描述手段,为区域船舶交通流形态特征、运行指标的提取,以及交通组织及规划提供了一种新的研究方法和理论依据.
1 船舶交通流形态特征概述
1.1 船舶交通流形态特征分析
形态,也可以称作形式或状态,是指事物存在的样貌,或在一定条件下的表现形式.形态是可以掌握的、感知的、理解的[14].船舶交通流的形态特征是指,在某一区域范围内某时刻或某时段的所有船舶地理位置及其行为的空间分布形式.通过船舶AIS历史轨迹数据能够在一定程度上体现船舶交通流的形态特征以及演变过程[15-16].
船舶交通流形态特征与船舶交通流动态特性对应,基于船舶交通流宏观特征以及静态特征,主要表现为某一水域船舶交通流的方向、宽度、交叉会遇点、船舶密度分布、船舶航行轨迹分布、船舶交通流各向异性等.船舶密度分布直接反映了某一水域中船舶的空间分布;船舶航行轨迹分布是船舶运动路线的记录,是指某一水域内所有船舶运动路线的历史空间分布;船舶交通流各向异性是指某一水域内具有不同航行方向的船舶子交通流.可以从一定程度上反映该水域内船舶交通流的复杂程度和态势特征.
1.2 船舶交通流形态特征影响因素
根据船舶交通流形态特征的本质意义和表现形式,结合船舶本身的特性、船舶交通流的基本特征,以及船舶航行环境等.其中外部环境的相关因素为船舶交通流形态特征的主要影响因素,可以划分为自然环境影响因素、通航水域影响因素及船舶交通组织影响因素,见图1.

图1 船舶交通流形态特征影响因素图
2 区域船舶交通流空间不均匀性度量模型
2.1 建模流程
在定性分析了区域船舶交通流空间不均匀性的定义、特征、影响因素及演化机理的基础上.在本节研究中,通过构建区域船舶交通流空间不均匀性的度量模型,对区域船舶交通流空间不均匀性进行定量分析.建模流程及思路见图2.
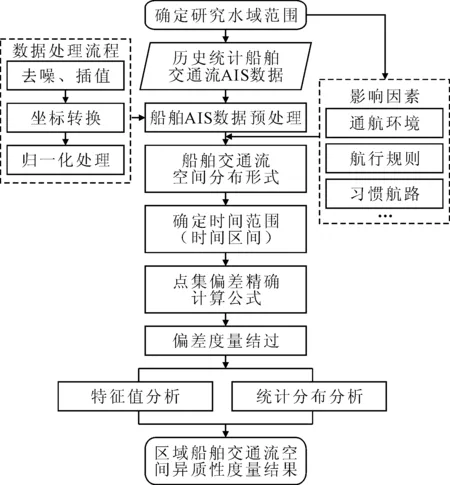
图2 区域船舶交通流空间不均匀性度量模型构建流程图
2.2 模型构建
2.2.1点集偏差理论
虽然有限点集在空间上的分布形式各不相同,但整体上可以区分为三种基本类型:聚集分布(clumped)、随机分布(random)、均匀分布(uniform),见图3.
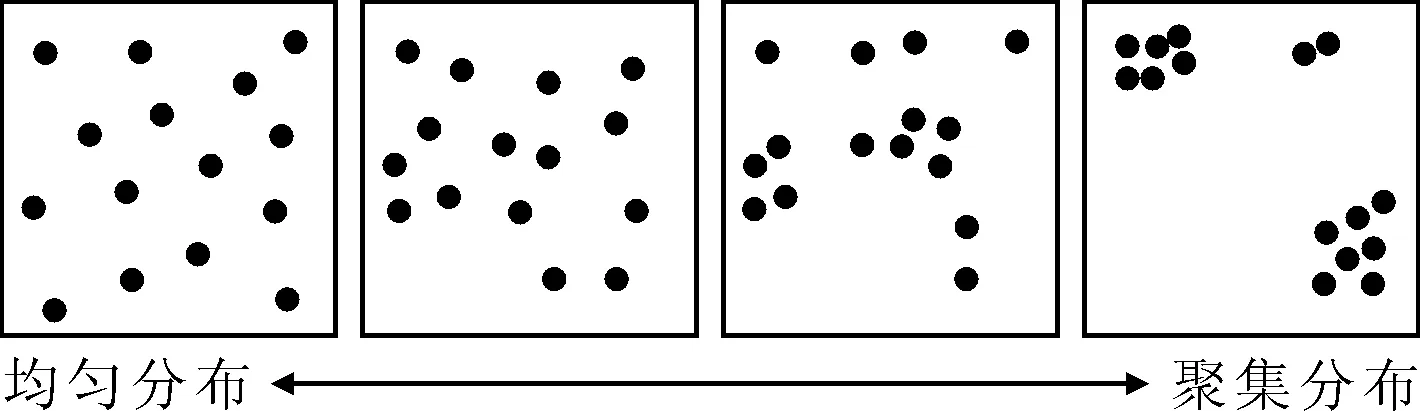
图3 空间点集分布形式
点集偏差描述了一个有限点集在某个区域(如区间[0,1]或d维正方体[0,1]d)中分布的一致(均匀)程度[17],其定义为
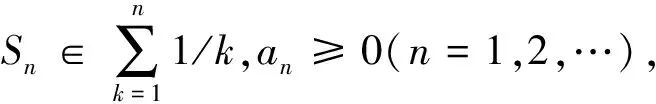
(1)
式中:γ为欧拉常数;系数e1+γ为最佳.基于van der Corput不等式,推导出的点集偏差精确计算公式为
设y1,y2,…,yn为单位m维空间Cm=[0,1]m中的n个点,任一向量y=(y1,y2,…,ym)∈Cm,记V(y)=y1,…,ym为矩形[0,y]的体积,n(y)为y1,y2,…,yn中落入[0,y]的点数,则
(2)
D称为点集|y1,y2,…,yn|在Cm中的偏差,在采用偏差度量均匀性时,一般认为偏差越大,则点集不均匀性越高,见图4.
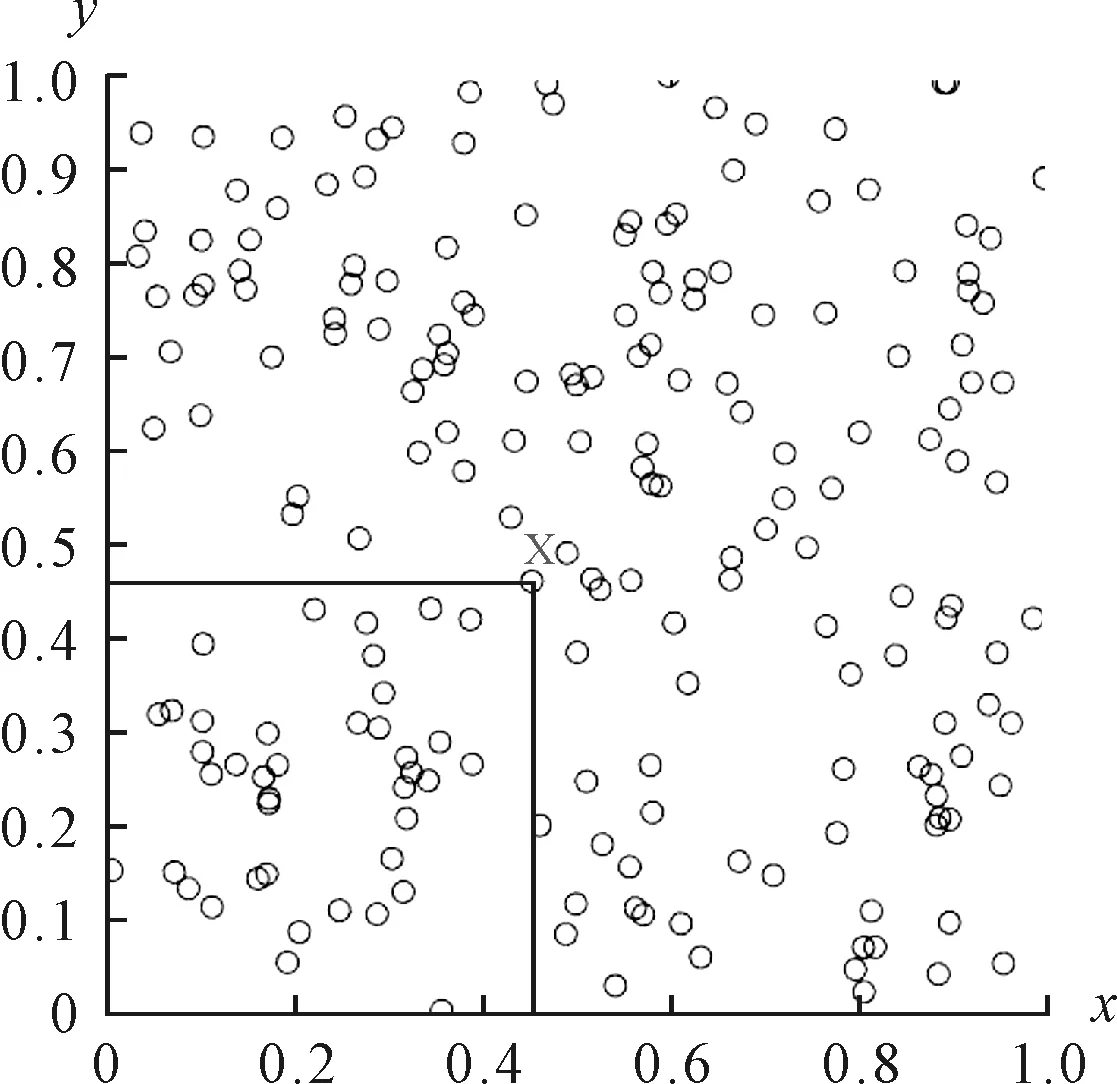
图4 点集偏差理论意义
在一个确定区域范围C内,随机生成分布的点集n,在另一个小范围选定的区域X内统计点集数量ny与点集总数量的比和区域V(y)与标准面积比之差的绝对值,选择所有结果中最大值作为该区域点集偏差的度量结果.
2.2.2区域船舶交通流空间不均匀性度量模型
根据上节中对点集偏差理论的基本分析,可以有效对二维空间坐标数据进行度量,但具有一定的局限性.点集偏差理论中推导出的精确计算公式仅适用于规则(矩形)区域范围内的点集偏差进行度量.但在实际情况中,更多研究的对象为不规则区域中点集的分布形式,见图5.
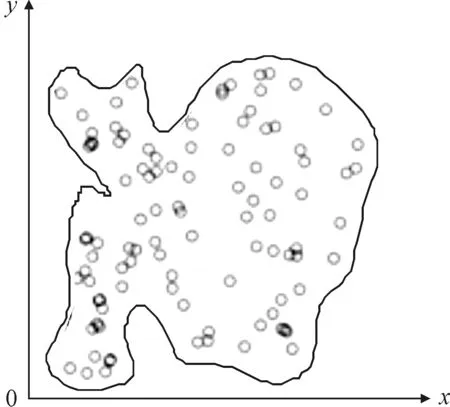
图5 不均匀区域范围内点集分布形式
根据点集偏差的精确计算公式和相关原理,构建的度量模型定义为
(3)
式中:相关参数与式(2)一致,但在对不均匀区域范围内点集分布形式计算中最难界定的是不规则区域面积S0的计算.在本研究中,采用网格化的方式进行离散化划分,将不规则的总体区域划分成m×m个相同的正方形区域,对于每一个顶点采用右上点的坐标表示,如点的坐标表示对应小正方形内点的坐标,式(3)中的S0用包含的总的正方形数表示,见图6.

图6 不规则区域的离散化表示
图中的灰色部分表示的为不规则区域面积S0,区域范围内所有点的集合为n.当计算A点处的偏差时,阴影部分面积可通过统计计算得到点集数量为ny,离散灰色格子数作面积V(y),即可以将不规则区域离散化处理,实现偏差度量计算.
3 实例研究
3.1 研究水域范围
选取长江口南港南槽与北槽航道交汇处水域为研究对象,矩形区域范围为东经121°40′48″~121°45′00″,北纬31°15′36″~31°21′36″,烟台港西港区进出港主航道,矩形区域范围为东经121°06′00″~121°09′00″,北纬37°43'00"~37°45'00",见图7~8.
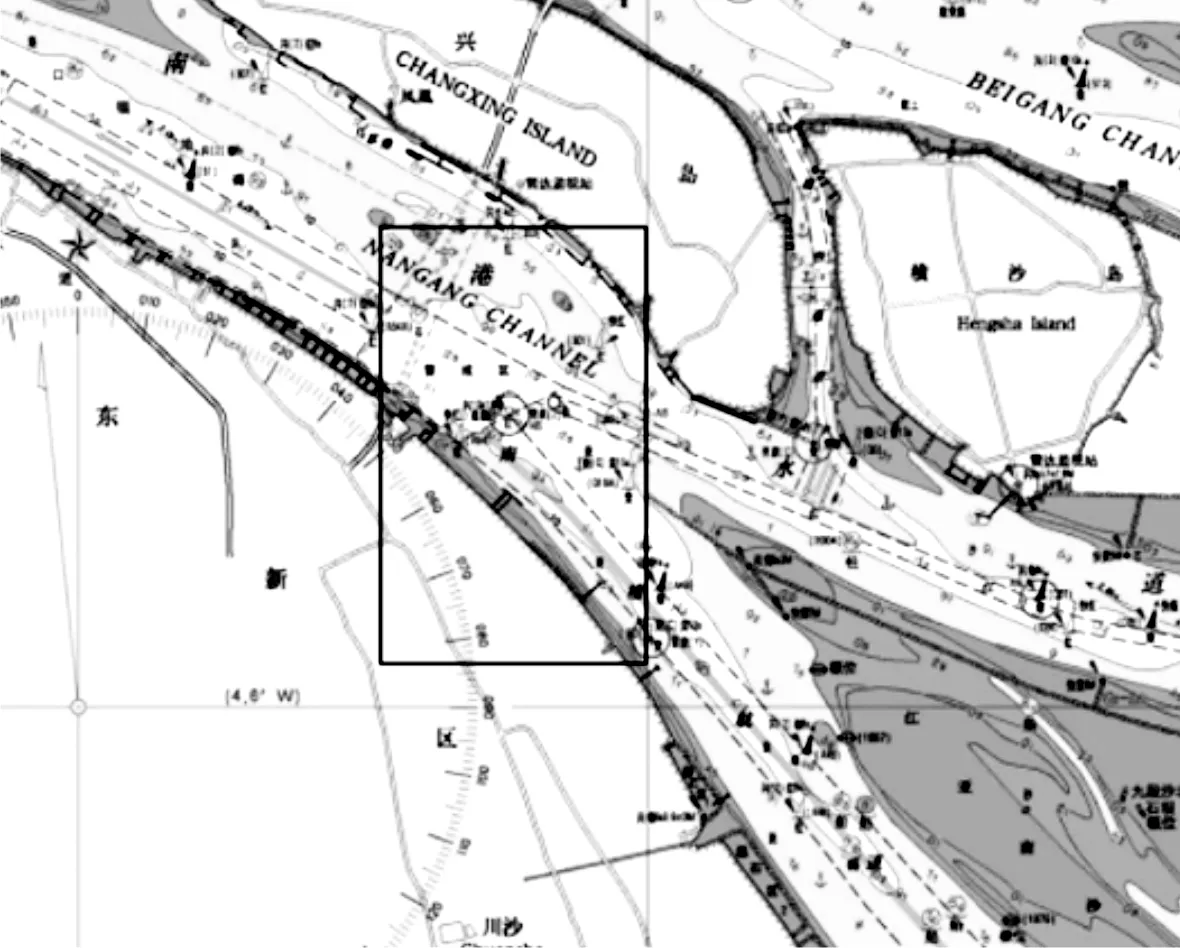
图7 研究水域地理位置——长江口
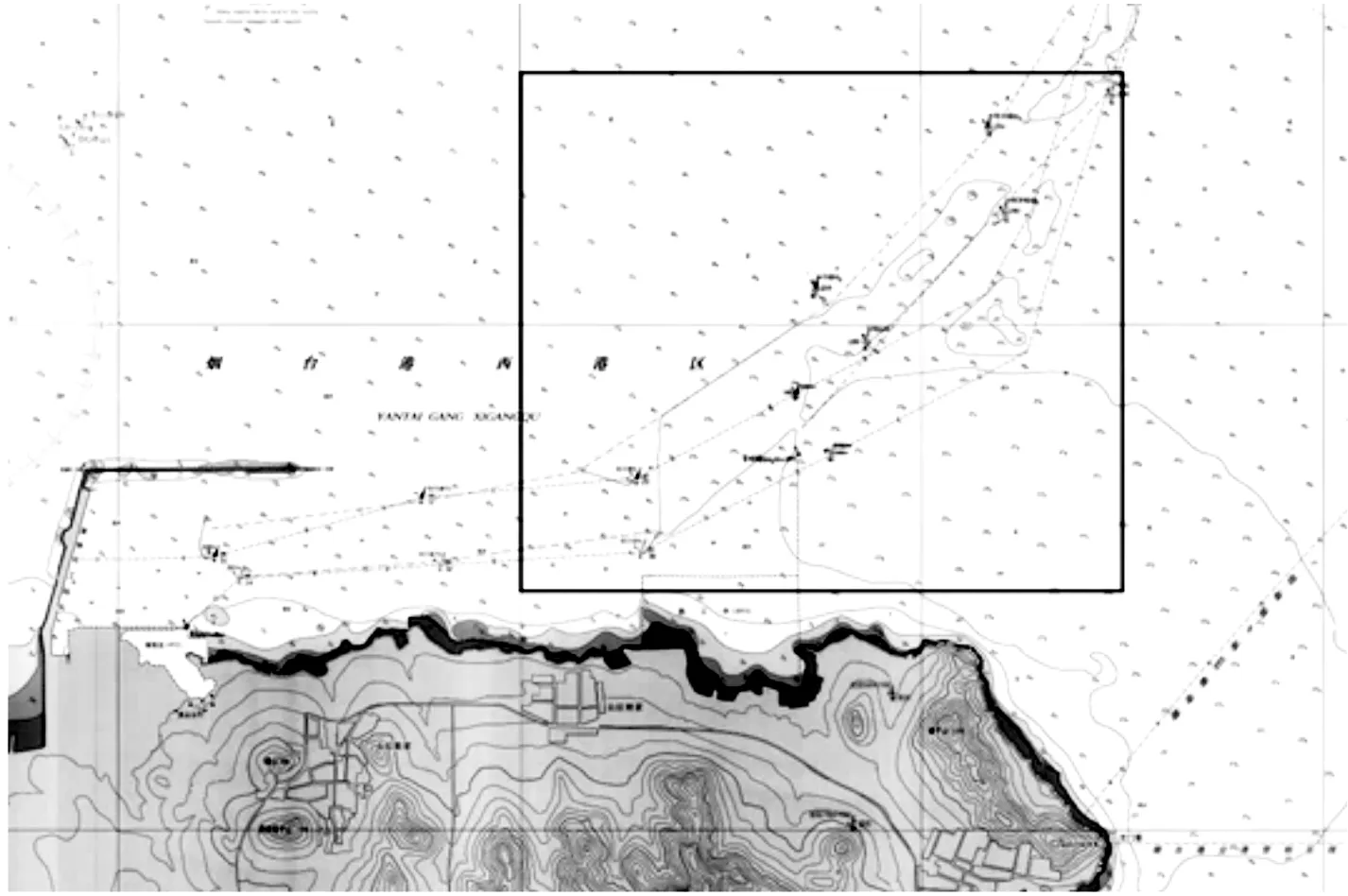
图8 研究水域地理位置——烟台西港主航道
研究水域均为繁忙水域,兼顾了船舶分道通航定线制水域(长江口南槽水域)、复杂交汇水域(烟台西港主航道水域)和港口水域(渤海湾水域),选取的各研究水域船舶交通流分布形式具有典型特征和代表意义,能够有效保障研究结果的普适性.
3.2 数据来源及预处理
选取2017年2月9—12日、2017年7月9—12日的长江口船舶AIS数据以及2017年3月9—12日烟台西港区主航道进出港水域船舶AIS数据进行船舶交通流分布形式的分析,为了得到满足研究条件的相关历史统计船舶AIS数据,需对数据进行预处理,流程见图9.

图9 船舶AIS数据预处理流程
3.3 区域船舶交通流空间分布形式
对数据转换、归一化等预处理手段将处理之前所得船舶交通流空间分布形式进行空间分布态势表征,见图10.
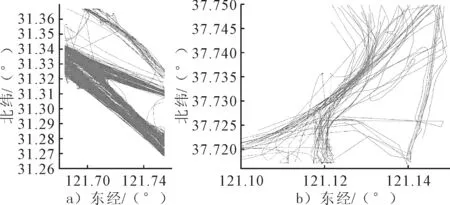
图10 研究水域船舶交通流分布形式
同时,为将AIS数据中的二维地理坐标信息表征为区域内多维点集的分布形式,进行了坐标转换及量纲的量化处理,将地理坐标信息转换为平面地理坐标,并将转换后的地理坐标进行归一化处理.选取同样一天船舶AIS数据作为处理后结果,其分布形式见图11.

图11 区域船舶交通流点集分布形式
3.4 区域船舶交通流不均匀性度量分析
由于船舶交通流分布形式的变化具有连续性以及每1 s内AIS统计数据集数据量较小.本文按照1 d内每10 min内统计的AIS数据地理坐标信息转换后的统计坐标点集集合的分布形式进行偏差计算.各天区域船舶交通流偏差度量结果见图12.
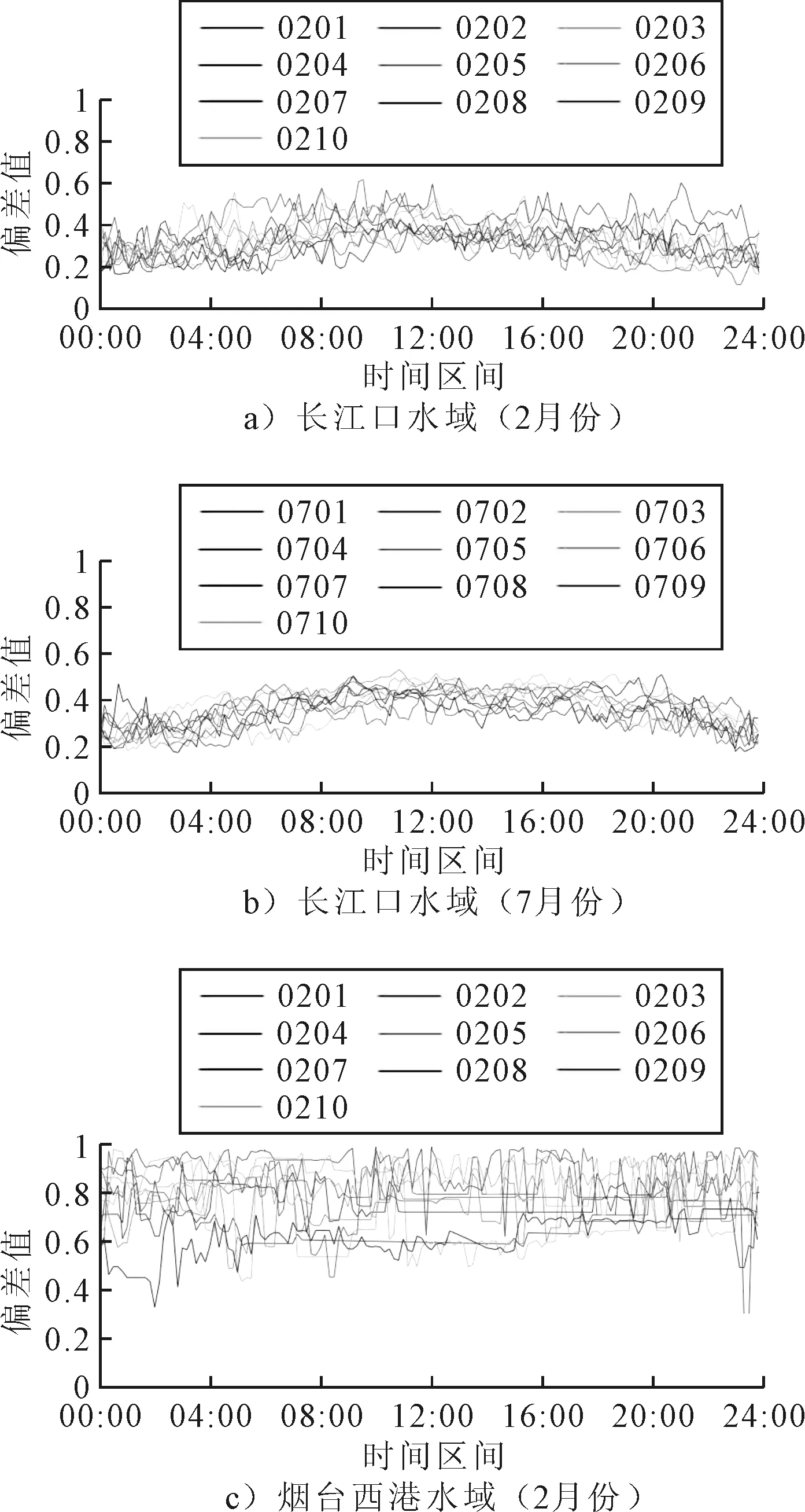
图12 连续10天偏差度量结果
根据偏差度量结果,可以得出以下结论.
1) 长江口水域的各天船舶交通流偏差度量结果分布在0.2~0.5,表明长江口水域船舶交通流空间分布不均匀程度一般,船舶交通流空间分布形式聚集程度不高,主要受到定线制及航道限制,其船舶交通流在空间分布上较为固定.同时,长江口水域船舶交通流偏差度量结果的分布及变化态势具有一致性,均存在一个升高、稳定然后降低的变化趋势,体现了航道内繁忙程度的变化形式.
2) 通过对比长江口水域2月份与7月份偏差度量结果可以发现,偏差结果及变化形式比较一致,可以体现不同季节在同一区域,时间对宏观船舶交通流整体的空间分布形态特征的影响不大.
3) 烟台西港区进出港水域处的各天船舶交通流偏差度量结果绝大多数偏差度量结果高于0.6,且存在较大波动,即可以表明该水域船舶交通流空间不均匀程度较高,船舶交通流在空间分布形式上的区域聚集形式较高,与烟台西港区主航道水域多数船舶会聚集在港口处的特征相对应,同时,由于船舶交通流密度不高导致了较为波动的度量结果.
与实际情况相结合,从偏差度量结果的整体趋势可以分析判断,与长江口南北槽交汇水域船舶交通流每日自08:00-20:00,12 h内船舶进出港繁忙程度的升高、维持繁忙程度然后降低的实际运行状态保持一致.烟台西港区港口水域由于考虑了船舶在港口停泊的情况,存在聚集程度较高的区域,且由于各时间段存在进入港口、通过的各类船舶,因此,度量的结果较高,波动较大.
3.5 偏差度量结果特征值分析
由图12偏差度量结果的整体变化无法有效揭示船舶交通流空间不均匀性度量结果所对应的船舶交通流分布形式.为了更好的揭示某区域特定时刻内船舶交通流的空间分布形式,由于烟台西港区主航道以及秦皇岛港口水域船舶交通流密度较低,在船舶交通流空间分布形式上存在波动,本研究中选取长江口2月9日、7月9日区域船舶交通流偏差度量结果进行对比分析.选取典型代表时间区间的偏差度量结果,见表1,同时截取对应时间段的船舶交通流空间分布形式,见图13.
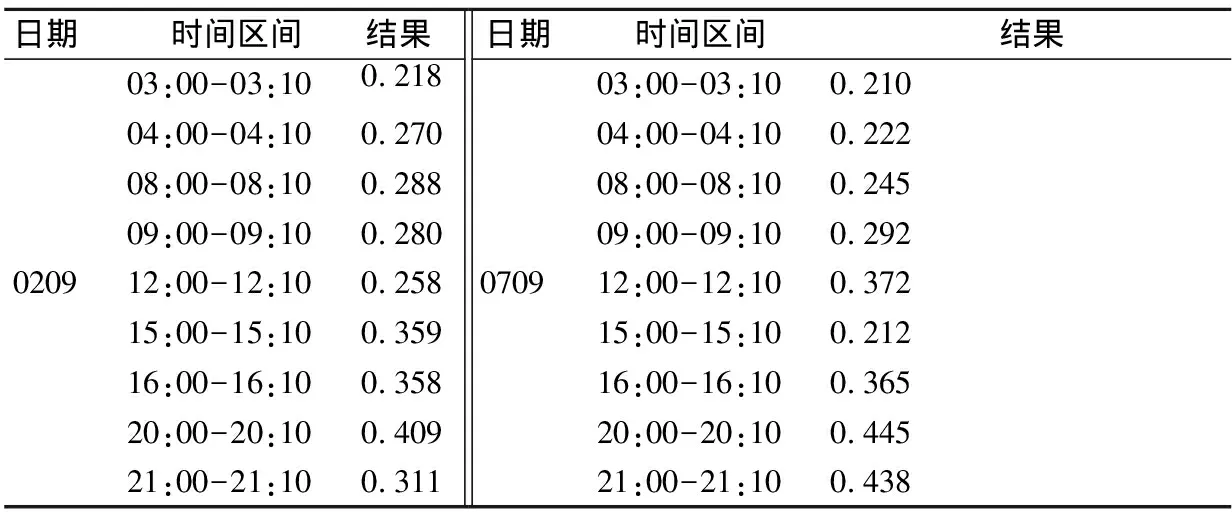
表1 偏差度量结果
结合表2和图13中偏差度量结果中船舶交通流分布形式分析可知:
1) 整体而言,选取的两天船舶交通流空间分布形式与船舶交通流整体分布形式、航道边界具有一致性.
2) 结合偏差度量结果分析可知,得到的偏差度量结果较高时,船舶交通流在分布形式上聚集程度较高,即其不均匀程度较高.
3) 对比两天中选取的特征度量结果以及船舶交通流分布形式可知,在分布形式的变化上较为一致,各天的偏差度量结果(不均匀程度)与船舶交通流密度关系不大.
4) 在选取的度量特征结果中,7月9日20:00-20:10时间区间偏差度量结果最高,船舶交通流区域范围内聚集程度最高;03:00-03:10时间区间偏差度量结果最低,在分布形式与航道边界分布一致,且较为均匀.
4 结 论
1) 通过系统分析船舶交通流空间分布的形态特征、相关影响因素和演化机理,提出并定性分析了区域船舶交通流空间分布不均匀性.
2) 在定性分析了区域船舶交通流空间分布不均匀性的基础上,运用点集偏差基本原理,构建了区域船舶交通流空间分布不均匀性度量模型.
3) 基于船舶AIS数据,通过相关数据预处理等手段,实现了区域船舶交通流空间分布不均匀性的量化分析,为宏观船舶交通流形态分布研究及态势研判提供理论依据及相关度量指标.
