船舶航向模糊控制器优化设计及仿真*
2019-07-01甘浪雄周春辉程小东
甘浪雄 邓 巍 周春辉* 程小东
(武汉理工大学航运学院1) 武汉 430063) (内河航运技术湖北省重点实验室2) 武汉 430063)
0 引 言
随着海上“丝绸之路”经济带的开通,我国航运贸易进一步发展,船舶的大型化、高速化及智能化趋势明显.船舶航向控制作为船舶智能化控制的重点与前提,一直都受到国内外相关学者的广泛关注.由于船舶的运动具有非线性、时变不确定性及时滞性等特点,船舶的航向控制实质上是一种非线性控制的过程.船舶航向控制器研究初期,采用PID(proportion integration differentiation)控制来实现船舶航向的控制,传统的PID航向控制器具有控制稳态精度高的优点,但是难以满足非线性系统控制要求,且其PID参数调节与整定过程较为复杂.随后模糊航向控制器因其动态性能好、稳定性强、对非线性系统控制能力强等优点而被广泛使用,但是其仍然存在控制精度不足,模糊规则的计算复杂性随着输入输出增多而增大等缺点[1-2].
目前国内外相关学者有关模糊PID控制的研究较多,王鸿健[3]在传统PID 控制的基础上利用模糊控制器动态调节PID控制参数Kp,Ki,Kd,使得航向控制效果得到了一定的改善,并提升了控制器的抗干扰能力.杨世勇等[4]在对模糊控制以及PID控制进行对比分析的基础上,提出了一种模糊PID复合控制器,控制器根据输入偏差范围自动切换控制模式,控制性能较好,精度较高.Savran[5]设计了一种新的多变量预测模糊比例积分微分(F-PID)控制系统,采用预测控制动态调节F-PID控制器参数,并通过在线训练以提高预测精度.仿真表明,该控制系统具有自适应、抗噪声,以及抗干扰性.陈小强等[6]结合模糊控制、PID控制和预测控制各自的优点,利用模糊控制对PID控制器的参数进行在线调节,同时引入预测控制达到提前调整的目的,设计了适合高速列车速度跟踪控制的预测模糊PID控制器.刘军等[7]采用一种利用变宽度与变形状的隶属度函数构成的模糊规则的模糊PID 控制器,实现了对转子系统的非线性恢复力的处理和非线性振动的完全控制.以上文献均验证了模糊PID控制器在非线性系统中进行控制的可行性.
针对船舶航向控制缺乏前馈调节的问题,利用航向成形算法对初始航向以及目标航向进行运算处理,当航向偏差角度较大时,采取较大的转向角速度以缩短转向所需时间;当航向偏差角度较小时,则采取较小的转向角速度以控制船舶能够精确达到设定航向.基于船舶航向控制器模块,结合模糊控制器与PID控制器的优点,设计了调节系统控制量的模糊PID控制器(Fuzzy-PID控制器),Fuzzy-PID控制器根据航向偏差范围选择利用模糊推理的方法或PID控制来实现系统控制,具有良好动态性能和较高的控制精度.在航向成形算法进行航向前馈调节的基础上,利用不同控制器在MMG模型下进行仿真分析,通过仿真结果验证了航行成形算法进行转向前馈调节的可行性及有效性,通过比较传统PID控制器、模糊控制器以及Fuzzy-PID控制器结果得出了Fuzzy-PID航向控制器的优越性.
1 船舶航向控制系统结构
在船舶航向控制系统中,首先输入初始航向及目标航向,利用航向成形函数计算并输出成形航向i.然后将航向偏离值ψr作为船舶航向控制器的输入变量,控制舵角δ的变化;最后将舵角δ输入到MMG船舶运动模型实现改变船舶航向.船舶航向控制系统结构图见图1.
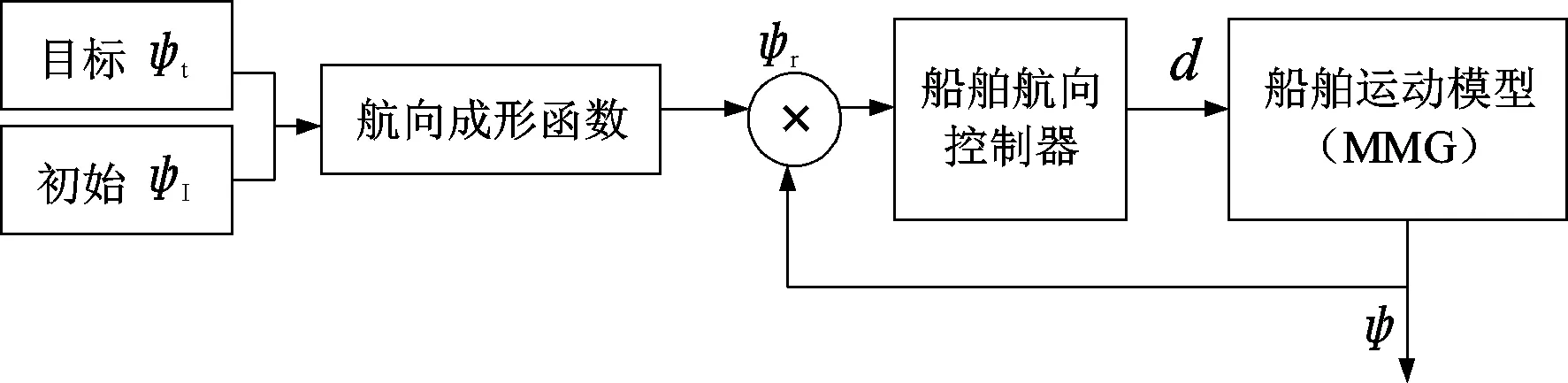
图1 船舶航向控制系统结构图
1.1 航向成形函数
船舶在实际转向操作过程中,当航向偏差角度较大时,通常需要采取较大的转向角速度以缩短转向所需时间;当航向偏差角度较小时,则通常采取较小的转向角速度以控制船舶能够精确达到设定航向,因此,转向角速度可以设置为
rd=aerfa×rmax
(1)
式中:aerfa据航向改变量确定的相应转向角速度权重,具体确定数值见表1.
在船舶转向过程中,转向速率会受到舵角的影响,船舶的转向速率与舵角关系为
r=K·δ
(2)
式中:r为船舶转向速率;K为野本模型中的增益系数;δ为舵角.
由此可计算出船舶舵角为35°时的转向角速度rmax为0.514(°)/s.
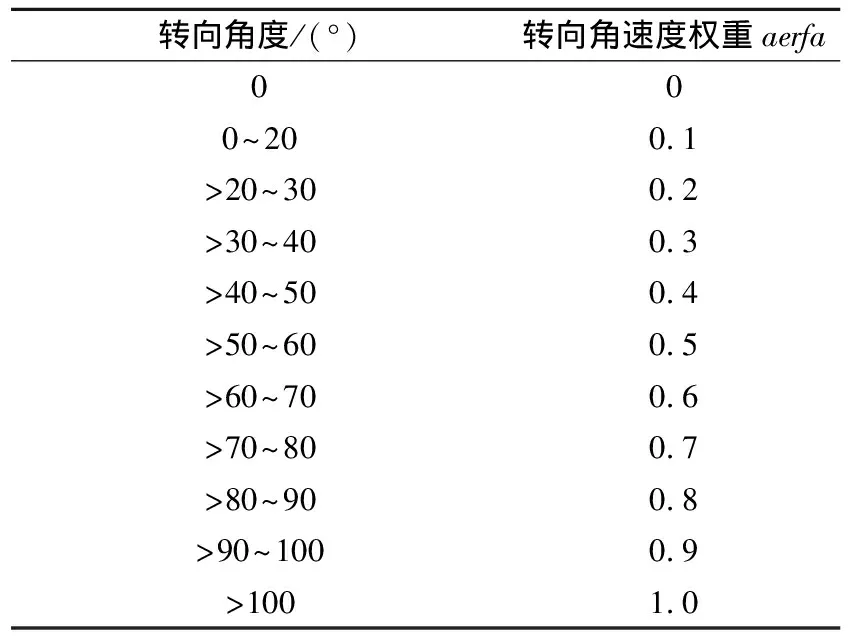
表1 转向角度与转向角速度权重对应表
1.2 分离型船舶运动模型
船舶操纵运动数学模型分为整体型模型、分离型模型以及响应模型三种.其中,分离型模型可以利用目前已发表的试验数据进行计算,对于不具备试验手段的研究者,利用该建模方法也可以构建精度较高的船舶运动模型,故选取分离型船舶运动模型进行船舶运动模型建立与仿真.
分离型数学模型主要是指MMG模型,是日本数学模型建模小组(manoeuvring mathematical model group,MMG)于20世纪70年代末提出[8],也是目前国际上比较流行的一种船舶运动数学模型.该模型是船舶整体型模型的简化,考虑了船、桨、舵的相互影响,它强调各个水动力导数的物理意义,剔除了一些由模型试验结果表明不重要的水动力导数[9].
采用随船坐标系,随船力矩计算为
(3)
式中:m为船舶质量;u为船舶前进速度;v为船舶横移速度;r为船舶转首角速度;Izz为船舶绕z轴的惯性矩;xc为船舶中心在坐标系中x轴坐标值;下标H,P,R分别表示船体、螺旋桨和舵;X,Y,M分别表示船舶沿x,y轴受力,以及船舶沿z轴力矩,由于螺旋桨的横向力YP及其对船重心的力矩MP很小,可以不考虑.
1) 惯性水动力和力矩 船舶在理想无限流场中运动时,会产生流体反作用于船体的惯性流体力.在船舶运动研究中,通常将其简化为船体的附加质量与附加惯性矩[10].
(4)
(5)
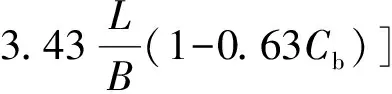
(6)
式中:L为船长;B为船宽;d为船舶吃水;Cb为船舶方形系数.
2) 黏性水动力和力矩 所采用的黏性水动力计算参照文献[8]中井上模型与贵岛模型相关的计算公式进行计算.
3) 螺旋桨推力 MMG模型中螺旋桨推力计算模型为
XP=(1-tP)ρn2DPKT(JP)
(7)
式中:tp为拖船螺旋桨推力减额分数;ρ为水密度;DP为螺旋桨直径;KT为螺旋桨推力系数;JP为进速;n为螺旋桨转速.
4) 舵力和力矩 MMG模型中舵力和力矩计算模型为
(8)
式中:FN为垂直于舵叶平面的正压力;tR为舵力减额分数,估算公式为(1-tR)0.738 2 -0.053 9Cb+0.1755Cb2;αH为操舵诱导船体横向力修正因子;xH为操舵诱导船体横向力作用中心到船舶重心距离.
2 船舶航向控制器设计
2.1 航向模糊控制器
模糊控制器(fuzzy controller)是一种语言控制器,针对系统的模糊特性如不完全性、不确定性以及非线性等,通过模拟人的控制经验与策略,对一些难以利用数学模型精确描述的过程进行控制,基本结构包括输入变量的模糊化、模糊算子的应用、运用模糊蕴涵进行模糊推理、模糊结果的聚类以及反模糊化[11].
航向模糊控制系统中,利用航向偏离差值e以及差值变化率ec作为输入变量,利用其控制船舶舵角的变化.模糊控制器结构见图2.
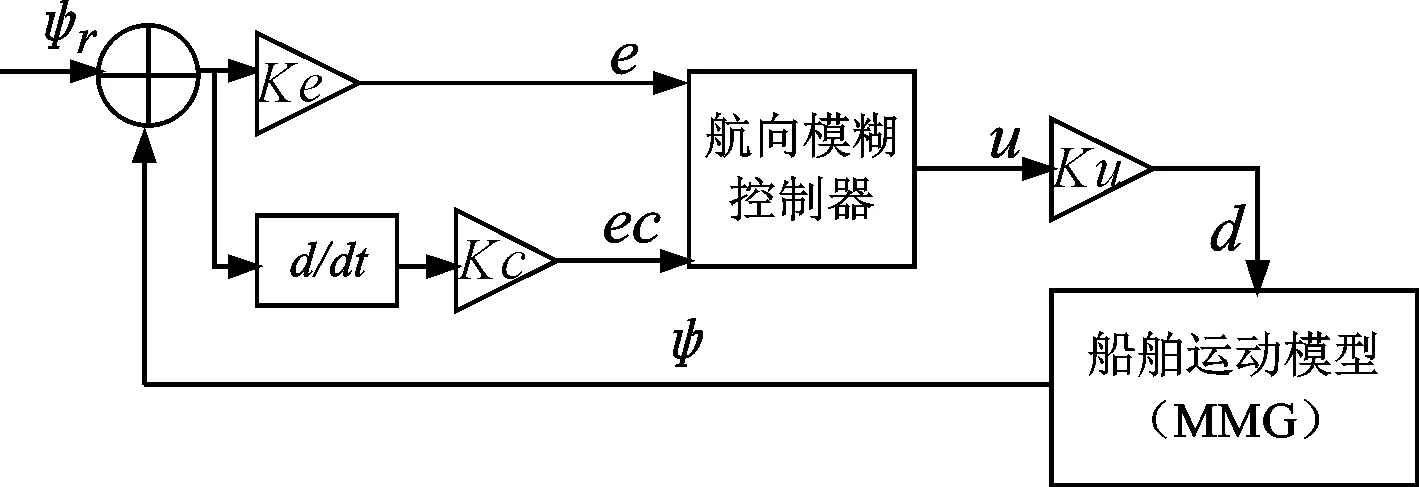
图2 船舶航向模糊控制器结构图
模糊控制器设计步骤如下.
步骤1设定输入输出变量取值范围 模糊控制器航向偏离差值e及差值变化率ec取值范围是[-6,6],输出变量u取值范围为[-3,3].控制器的语言值设计为
e=[NB,NM,NS,ZE,PS,PM,PB]
ec=[NB,NM,NS,ZE,PS,PM,PB]
u=[NB,NM,NS,ZE,PS,PM,PB]
步骤2确定系统的量化因子和比例因子 设航向偏离差值e、差值变化率ec以及输出变量u取值范围分别为[-xe,xe],[-xec,xec],[-xu,xu],则Ke=6/xe,Kc=6/xec,Ku=xu/3.
步骤3确定隶属度函数 隶属度函数的确定直接影响到控制器的控制效果.航向偏离差值e及差值变化率ec选用较为简洁的三角隶属函数(trimf),见图3.输出变量u选用π形隶属函数(pimf),见图4.

图3 航向偏离差值以及差值变化率隶属度 图4 输出变量u(舵角)隶属度
步骤4确定模糊规则库 模糊规则库是总结控制专家的控制经验以及人为的控制决策整理而成,所设计的航向模糊控制规则见表2.
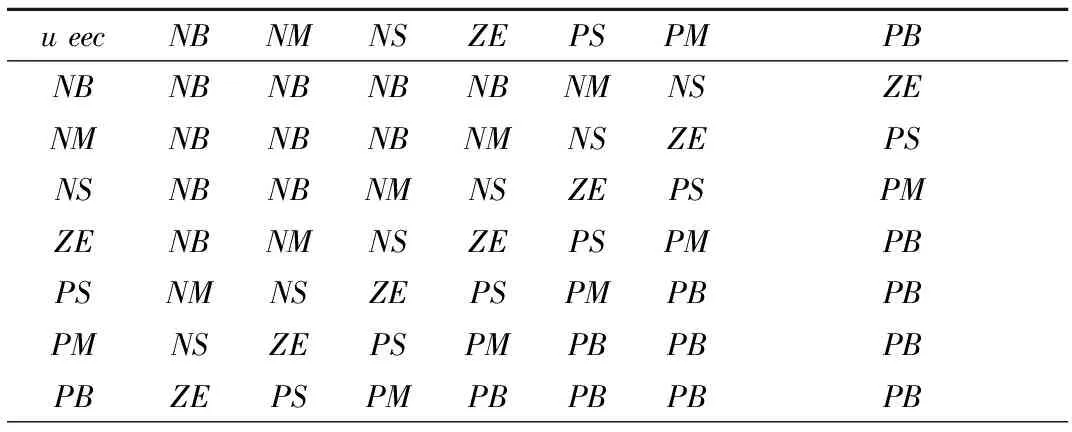
表2 航向模糊控制规则库
2.2 航向Fuzzy-PID控制器
Fuzzy-PID控制器是基于模糊控制器及PID控制器基础上所设计的,该控制器的特点是在航向偏差较大(>30°)时利用模糊推理的方法调整系统控制量u,保证航向偏差较大时的控制效率和速度,而在航向偏差较小(≤30°)时转换为PID控制来保证控制精度与稳态.Fuzzy-PID控制器的控制结构见图5.
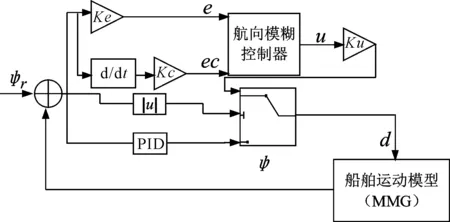
图5 调节系统控制量的模糊PID控制器结构图
其中:PID控制器参数根据运算调试得到其取值为Kp=0.17,Ki=0.0004,Kd=1.0.
3 仿真实验
航向控制仿真在MATLAB R2014a软件SIMULINK模块上进行,采用的船舶运动模型是1.2中的分离型船舶运动模型(MMG),控制船舶参数见表3.
表3 控制船舶参数表
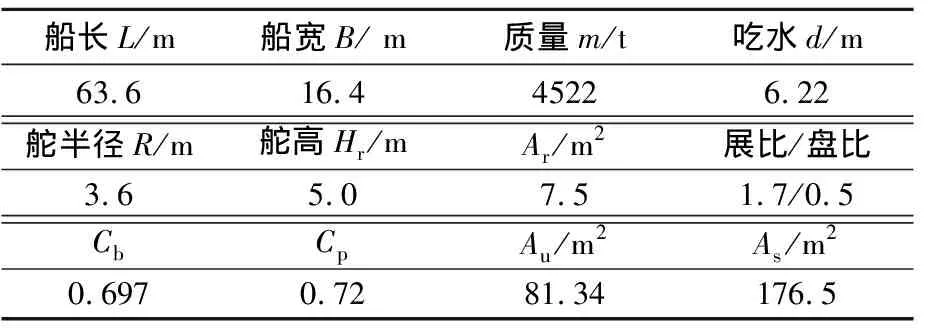
L/mB/ m m/td/m63.616.445226.22R/mHr/mAr/m2/3.65.07.51.7/0.5CbCpAu/m2As/m20.6970.7281.34176.5
注:Ar--舵面积;Cb-船舶方形系数;Cp-船舶菱形系数;Au-船舶纵向受风面积;As-船舶横受风面积.
首先,采用三种不同的转向角度(0°~90°,30°~90°,60°~90°)来验证航向成形算法的可行性以及合理性.其次对转向角度(60°~90°),使用传统PID控制器、模糊控制器及Fuzzy-PID控制器进行对比仿真,比较不同控制器在船舶转向过程中的转向角速度、舵角,以及航向变化情况.
3.1 多角度转向下的模糊控制器仿真
采用三种不同转向角度(0°~90°,30°~90°,60°~90°)利用航向模糊控制器进行仿真来验证航向成形算法的前馈调节作用.设计航向偏离差值e最大取π/2,差值变化率ec最大取rmax=0.514(°)/s,输出变量u最大取35π/180°.三种不同转向角度下的转向角速度权重、转向角速度以及模糊控制器参数见表4.
根据图2的船舶航向模糊控制器进行多角度转向仿真得到的仿真结果见图6~8.
由上述仿真结果可以得出:
1) 经过航向成形函数处理后,船舶能够以恒定的转向角速度(rd1=0.463,rd2=0.308,rd3=0.154(°)/s)进行转向,船舶大角度转向时转向角速度更快,超调更大,但耗时更短.小角度转向时转向角速度更小,耗时更长,但更加稳定精确.
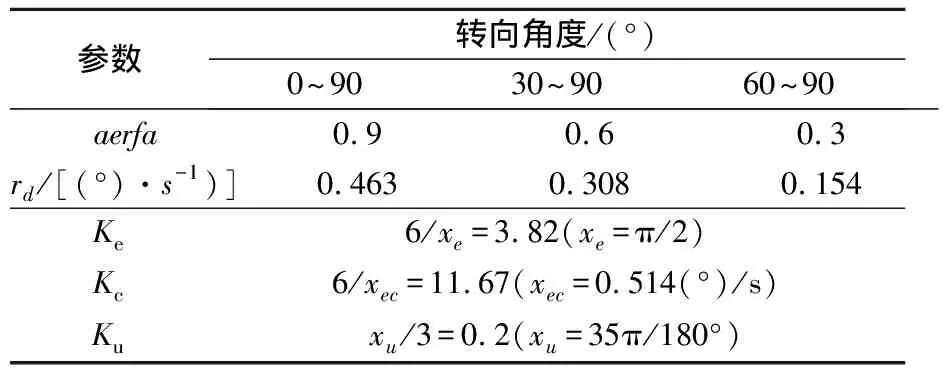
表4 多角度转向仿真参数
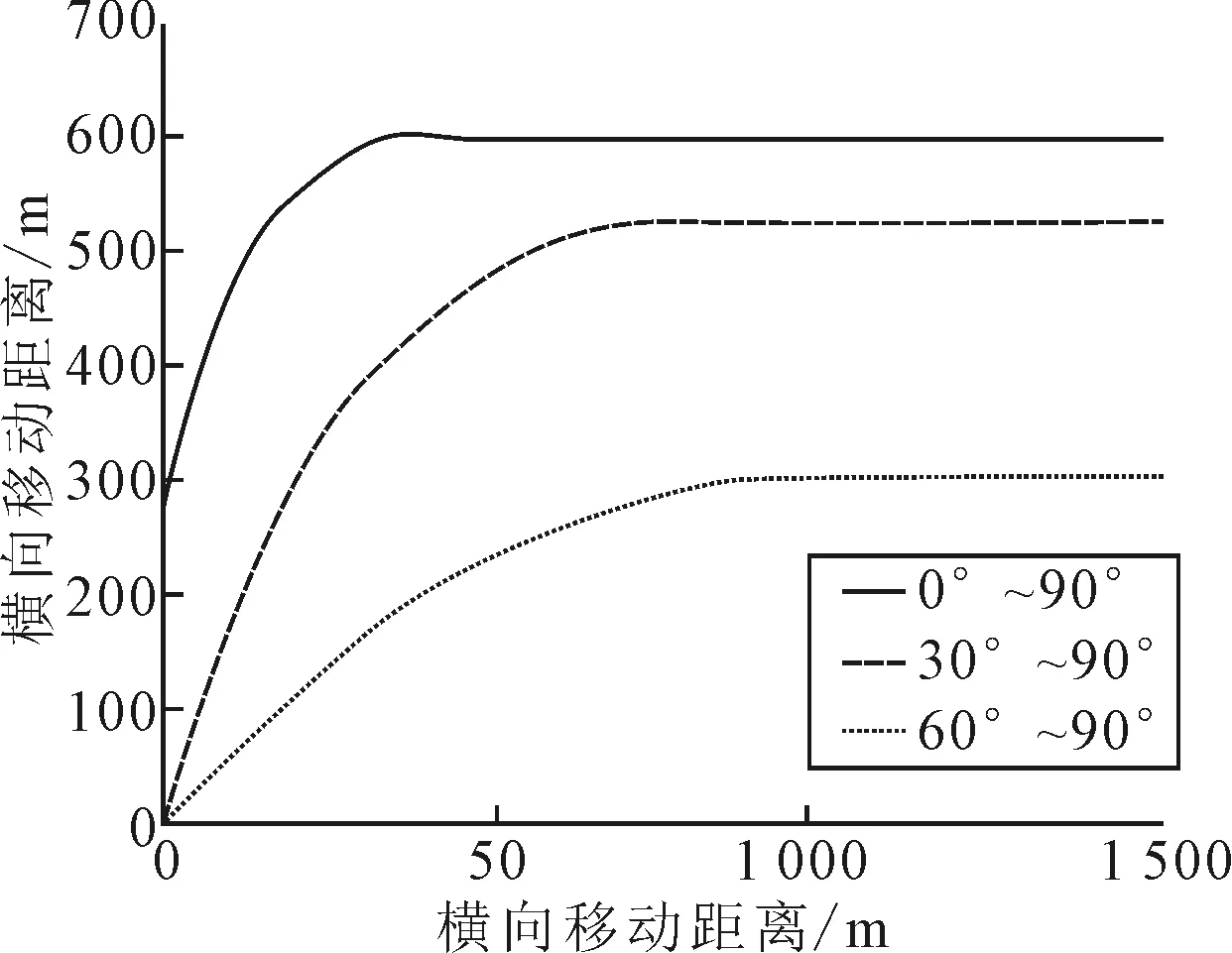
图6 多角度转向轨迹图

图7 多角度转向角速度图

图8 多角度转向仿真航向舵角变化图
2) 图8中舵角响应图表明,转向角度越大,所操舵角和回舵角度也越大,由操舵引起的船舶航向超调也更大.转向角度越小,所操舵角和回舵角度也越小,由操舵引起的船舶航向超调也更小.
多角度转向下的模糊控制器仿真验证了航向成形算法的正确性及有效性.当航向偏差角度较大时,模型能够采取较大的转向角速度以缩短转向所需时间;当航向偏差角度较小时,模型则采取较小的转向角速度以控制船舶能够精确达到设定航向.航向成形算法可以有效运用于船舶转向的前馈调节,使得船舶转向过程更加合理.
3.2 多控制器下的航向控制仿真
选用0°~90°转向进行仿真实验,采用相同的调节参数,分别利用传统PID控制器、模糊控制器以及Fuzzy-PID控制器进行航向控制仿真,对比分析三种控制器的控制效果,三种控制器在转向过程中的控制结果见图9~10.
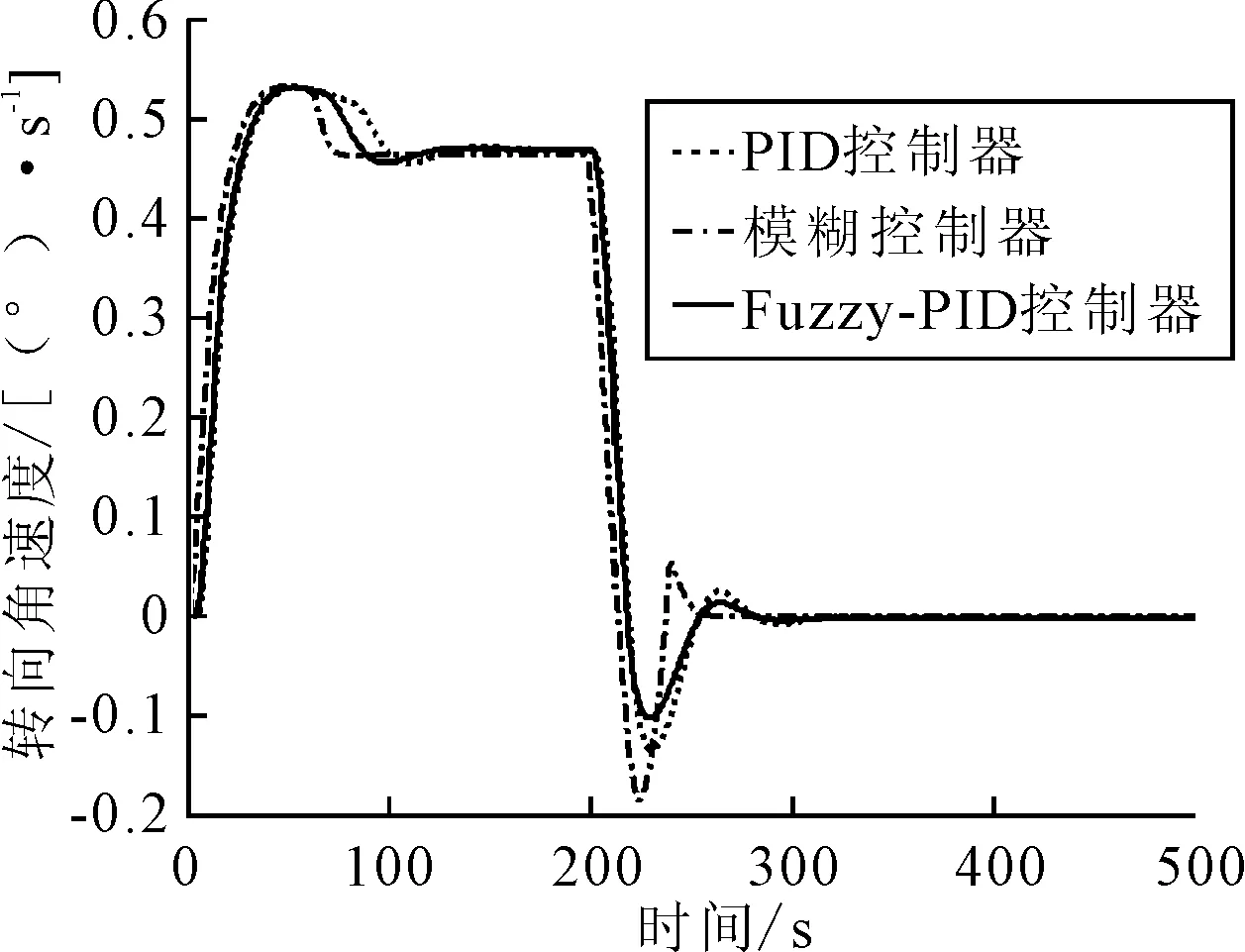
图9 转向角速度对比图
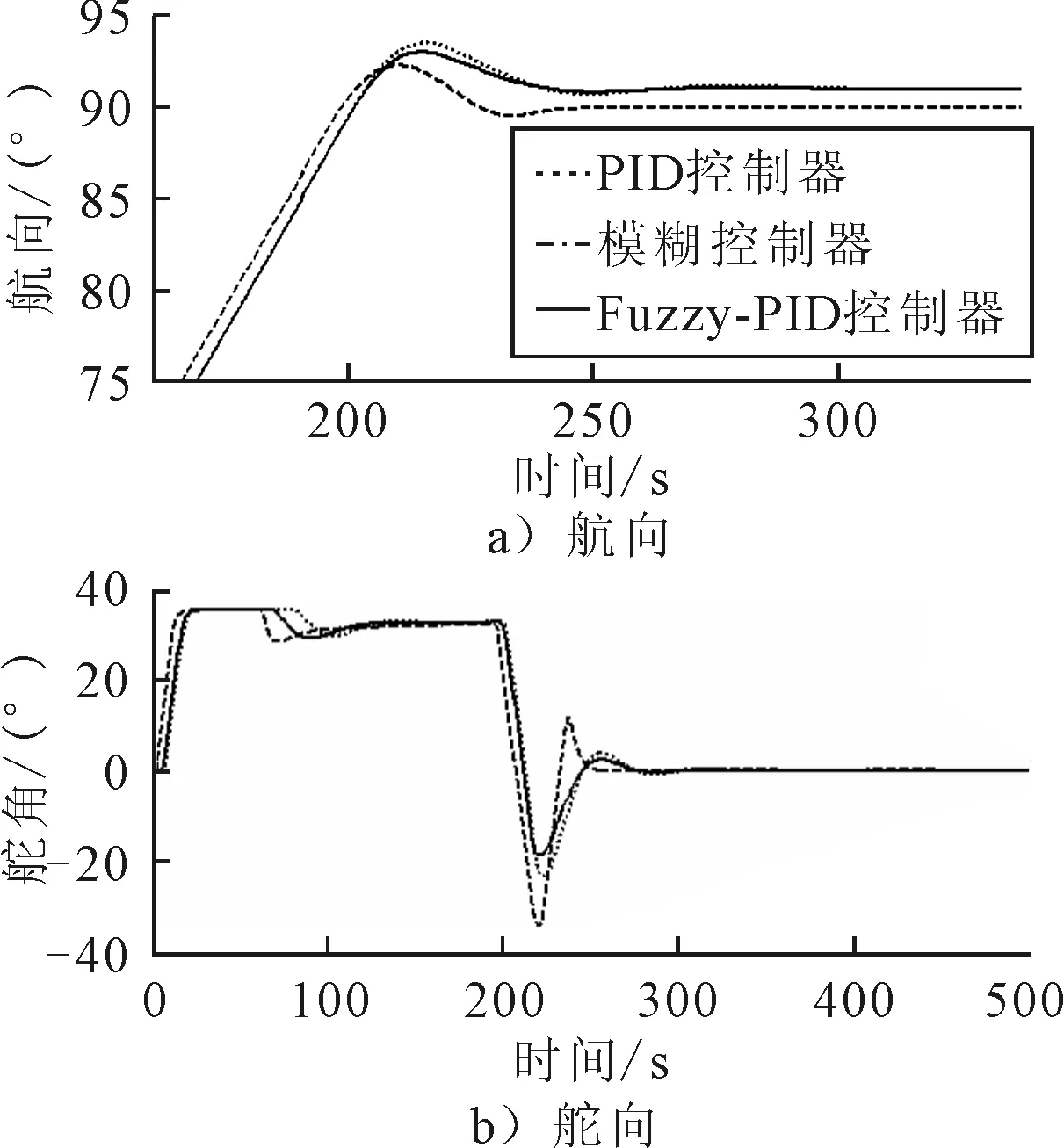
图10 转向仿真航向舵角变化对比图
由上述仿真结果可以得出:
1) 传统的PID控制器在设定的PID参数下能够有效实现转向操作,但是仍存在超调较大、转向操作较慢等缺点.
2) 模糊控制器在进行大角度转向控制时,转向速率快、动态性能好,但是在转向后期即小角度转向时存在精确度不足等缺陷.
3) Fuzzy-PID 控制器在进行转向控制时超调较小、转向操作及时,且在转向后期舵角更平稳、精确度更高,兼具模糊控制动态性能好与PID控制稳态精度高的优点.
4 结 束 语
针对船舶航向控制缺乏前馈调节的问题,首先基于航向成形算法对初始航向以及目标航向进行前馈调节,将成形航向偏离值作为船舶航向控制器的输入变量,利用其控制舵角变化,经过MMG船舶运动模型达到改变船舶航向的效果.其次为达到实际船舶控制的精度要求,结合相关文献设计了一个与实际转向过程较相符的模糊规则库,在模糊控制器与PID控制器基础上设计了Fuzzy-PID控制器,对船舶进行系统控制.
仿真结果表明航向成形算法可以有效运用于船舶转向的前馈调节,使得船舶转向过程更加合理.在实现转向控制的前提下,Fuzzy-PID控制器的舵角响应效果更合理,具有良好的动态性能和较高的稳态精度.
