“控制与设计”难点问题的分析与研讨
2019-06-27代超
摘 要:“控制与设计”是通用技术必修内容中公认的对专业依赖度最高的一个章节,但任课教师几乎都没有系统的学习过《控制论》《自动控制技术》《模拟、数字电子技术》等专业课程,本文针对“有检测就一定是闭环控制系统吗?”,“投篮(投飞镖、打靶)是开环还是闭环控制?”,“是不是闭环控制精度高,我们应尽可能地采用?”等难点问题做了分析与研讨。
关键词:难点问题;开环控制;闭环控制;干扰与反馈;控制框图
一、 研究背景
“控制与设计”是通用技术必修内容中公认的对专业依赖度最高、最难开展教学、争议问题最多的一个章节;与之矛盾的是,这是一门新兴学科,任课教师几乎都没有系统的学习过《控制论》《自动控制技术》《模拟电子技术》《数字电子技术》等专业课程,本文正是选取了其中的难点问题来进行分析与研讨,希望借此给大家解开困扰多时的疑惑。
二、 难点问题分析与研讨
【在开环控制系统中一定没有检测,反馈环节吗?如果有就一定是闭环控制系统吗?】
在开环控制系统中,如果有检测,反馈环节,是不能起到任何作用的。所以在人为设计、制造的开环控制系统中,就没有检测和反馈环节。但在非人为制造的开环控制系统中,就可能有这些环节,例如人开关电灯,人投篮球,其检测、反馈环节是存在的,我们不能要求人开关完电灯,投出篮球后眼睛不去看它。有人说不能看,一看就有检测和反馈,就成了闭环控制了,这个说法是荒谬的,因为这个反馈并没有形成较正作用,去较正被控对象。有的书中说,有无检测,反馈环节是区别开、闭环系统的重要因素,这个说法是不准确的。
【怎样判断一个控制系统是开环还是闭环控制系统?闭环控制的最终结果一定是被控量等于基准量吗?】
判断一个控制系统是否闭环,首先可以用系统有无抗干扰能力的方法来判断。因为干扰可使被控量偏离原来的值,闭环控制系统在检测到偏离值后,会自动进行校正,无抗干扰能力的系统不是闭环控制系统。
判断一个控制系统是否闭环,还可以用被控量有无跟踪基准量的能力来判断。把基准量改变一个量,系统经一段时间调控后仍然能使被控量接近基准量,这个系统就是闭环控制系统,如没有跟踪基准量的能力,就是开环控制系统。例如人骑自行车时,道路方向(基准量)不断改变,车头方向可以不断跟踪;又如导弹打飞机,飞机不断改变方向和位置,导弹照样可以跟踪空中飞机,这两个系统都是闭环控制系统。
在闭环控制系统中,控制是一个动态过程,只能说控制的结果是被控量不断接近基准量(期望值)。例如我们骑车时,前轮未必一定压在道路的中线上;导弹打飞机时,也可能有某一架敌机逃跑了,导弹没打中。
【投篮(投飞镖、打靶)是开环还是闭环控制?】
投篮时,发生了这样的情况:
第一次投掷:由于用力太大,篮球碰到了篮板上弹了回来,没有命中;
第二次投掷:吸取第一次的经验,减小了用力,但用力过小,篮球没有碰到篮圈;
第三次投掷:吸取了前两次投掷的经验,终于投中了。
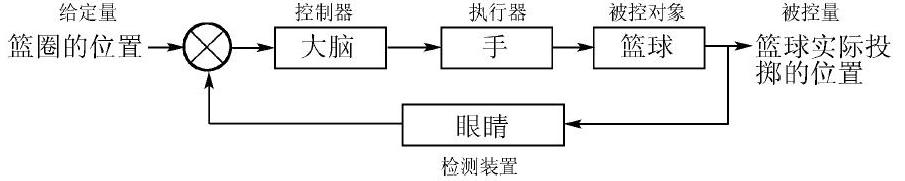
在这里,可以将人看作控制系统,眼睛把接收到的篮圈位置以及实际投掷位置等信息输送给大脑,经大脑分析和加工处理后,发出指令,指挥手投掷篮球,直到投篮命中。(如下框图所示)
所以,我们可以看出,类似的人参与其中的控制活动,若只进行1次是开环控制,而重复进行N次则是闭环控制!
当然,称其为闭环控制的前提是需要考虑投掷的次与次的间隔时间T1(控制系统中的环节中断时间)。控制系统中某环节中断的时间T1应远小干扰存在(或需调控校正)的时间T2,即T1T2,此时,T1相对于T2可以略去!例如,我们第一次、第二次、第三次投掷的间隔时间为3秒,并不影响这系统的正常运行和抗干扰性能,可看作是闭环控制系统;但假设我们第一次、第二次、第三次投掷的间隔时间变为1天,它就不再是闭环控制系统了!
【是不是闭环控制精度高,我们应尽可能地采用?】
有这样一个故事:联合利华引进了一条香皂包装生产线,但这条生产线有个缺陷:常常会有盒子里没装入香皂。他们只好请了一个高级工程师设计一个控制系统来分拣空的香皂盒。工程师综合采用了机械、微电子、X射线探测等技术,设计了一套闭环控制系统,每当生产线上有空香皂盒通过,两旁的探测器会检测到,并且驱动一只机械手把空皂盒推走。
中国南方某乡镇企业也买了同样的生产线,老板发现这个问题后发动工人想解决办法。工人果然想出了办法:在生产线旁边放了台风扇(开环控制),空皂盒自然会被吹走。
通过这个故事,大家肯定能达成共识:闭环控制精度高,成本也高;开环控制相对精度低,但是成本也低。使用哪一种控制系统,还需要根据实际情况,综合优选。
三、 结语
专业知识的欠缺和缺少必要的资源,造成我们师生在“控制与设计”的教与学过程中产生了困难,本文作者通过长期的一线教学和与广大教师的深入沟通,总结了该章节内容中存在难点的问题,以自己“自动控制技术”专业的背景做出了相应的分析与研讨,希望能帮大家解开困扰多时的疑惑。
参考文献:
[1]顾建军.技术课程标准(实验)解读[M].武汉:湖北教育出版社,2004.
[2]顾建军.通用技术教学研究与案例[M].北京:高等教育出版社,2007.
作者簡介:
代超,云南省昆明市,云南师大附中。
