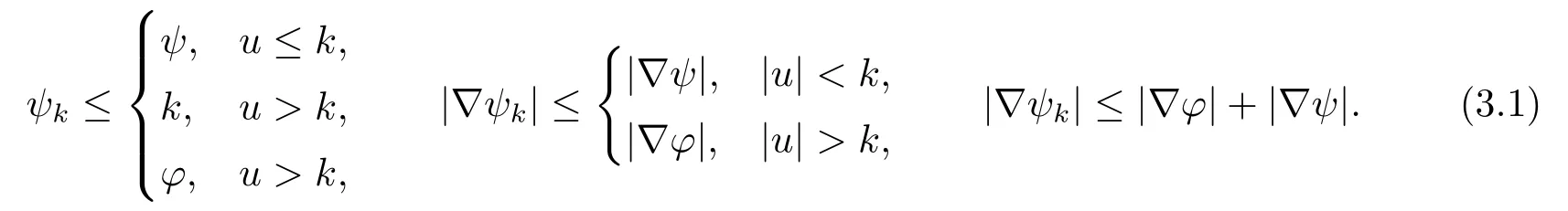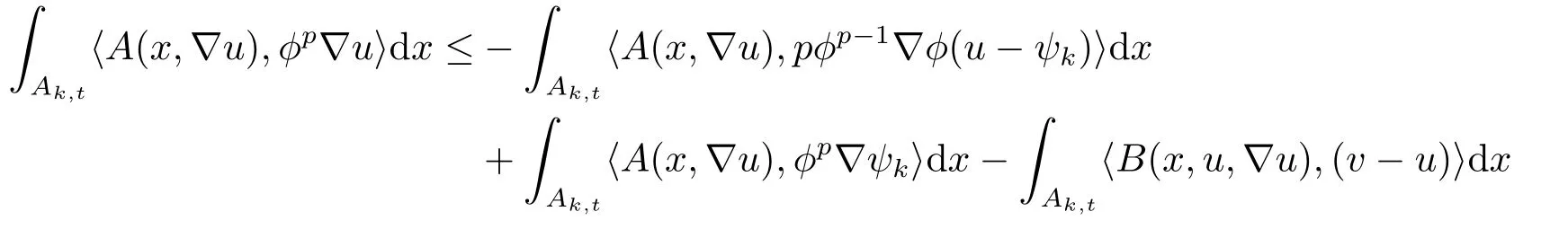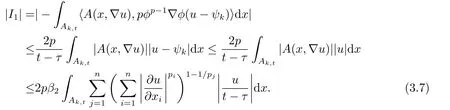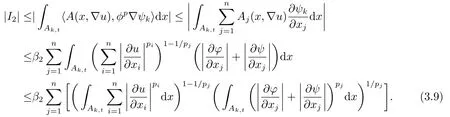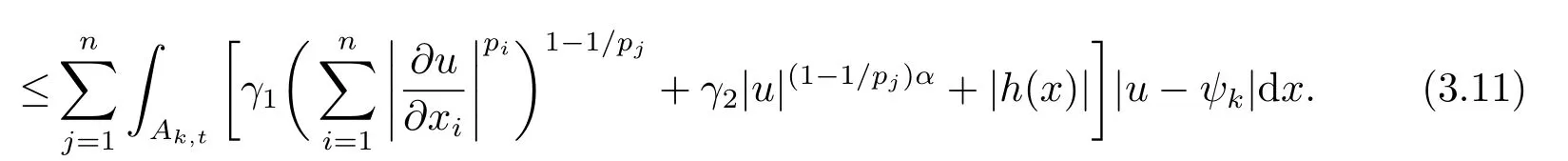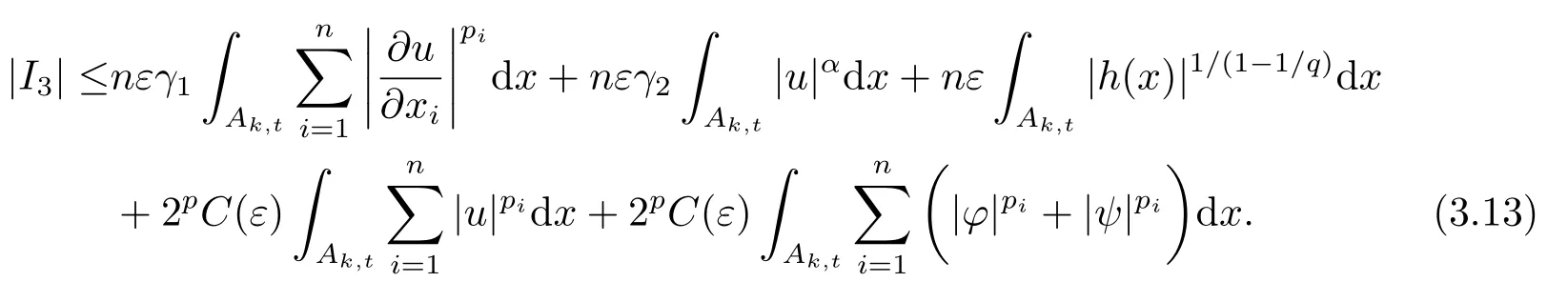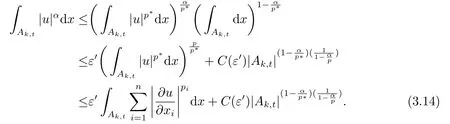各向异性椭圆方程双边障碍问题解的正则性
2019-06-27谢素英杨超
谢素英,杨超
(杭州电子科技大学理学院数学系,浙江 杭州310018)
1.引言
近年来,人们对椭圆方程及其障碍问题的弱解的正则性研究有了很多结果.对于各向同性的情形,即解的偏导数在各个方向上具有相同的可积指数情形,李工宝和Martio在文[1]中研究了齐次A-调和方程−divA(x,Du)=0的双边障碍问题弱解的全局正则性;佟玉霞等在文[2]中研究了A-调和型方程−divA(x,u,Du)=0的双边障碍问题弱解的局部和全局可积性;刘保相等在文[3]中研究了非齐次A-调和型方程−divA(x,u,Du)=f(x)的双边障碍问题弱解的局部有界性.对各向异性的情形,即解的偏导数在各个方向上具有相异的可积指数情形,Giachetti和Porzio在文[4]中研究了各向异性最小化函数I(u)=∫Ω f(x,u,Du)和各向异性拟线性椭圆方程弱解的局部正则性;高红亚等推广了文[4]的结果,在文[5]中研究了各向异性拟线性椭圆方程−弱解的局部正则性.最近,各向异性椭圆方程障碍问题的弱解受到极大关注.对于单边障碍问题,高红亚等在文[6-7]中分别研究了各向异性A-调和方程−divA(x,Du)=0弱解的局部正则性和拟线性方程divA(x,u,Du)=divf(x)弱解的全局正则性;谢素英,廖敏在文[8]中研究了拟线性方程−divA(x,Du)=B(x,u,Du) 弱解的局部正则性.但是,关于各向异性椭圆方程(1.1)双边障碍问题弱解的局部正则性尚未得到研究.本文受文[1-3,6-8]的启发,构建了适合各向异性双边障碍问题的检验函数,使用各向异性的逆Hlder不等式和Sobolev不等式,得到了非齐次椭圆方程(1.1)双边障碍问题弱解的局部正则性,将文[6-8]中各向异性的单边障碍问题的相关结果推广到了双边障碍问题的情形.
设Ω ⊂Rn(n ≥2)是有界开集,x0∈Ω,t >0,记Bt=Bt(x0),Bt(x0) 是以x0为中心,t为半径的球.对k >0 和可测函数u(x),设Ak={x ∈Ω:u(x)> k},Ak,t=Ak∩Bt.而且如果m

考虑各向异性Sobolev空间

局部各向异性Sobolev空间

考虑下面的非齐次椭圆方程

其中A(x,ξ):Ω×Rn→Rn,B(x,u,ξ):Ω×R×Rn→Rn均为Carathodory函数,满足:
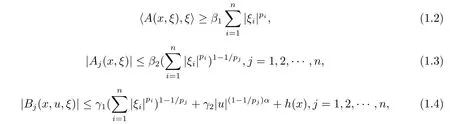
这里x ∈Ω,β1,β2,γ1,γ2均为正的常数,函数h(x)∈Lrloc(Ω),h(x)>1,q ≤α
设φ,ψ为Ω中任意取值于R∪{±∞}的函数,θ ∈W1,(pi)(Ω),

这里函数φ,ψ为两个障碍,θ为边值.
定义1.1函数称为方程(1.1)的-障碍问题的弱解,如果对任意的有

2.引理和主要结果
引理2.1[9]设有界非负函数f(τ)定义在0≤R0≤t ≤R1,假如对于R0≤τ ≤T ≤R1,有
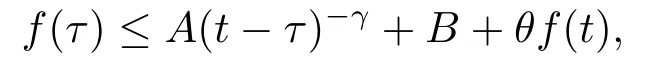
这里A,B,γ,θ为非负常数,且0≤θ <1,则存在一个常数C=C(γ,θ),使得对每个R,ρ,R0≤ρ 引理2.2[4]设这里p,,和r满足 假设对每个k ∈N和R0<ρ 这里C是一个正的常数,它仅仅依赖于n,pi,r,R0,R1和|Ω|,且γ是实数,那么(Ω),其中 定理2.1若方程(1.1)满足条件(1.2),(1.3),(1.4),且则对是方程(1.1)的-障碍问题的弱解,有其中 在证明过程中,常数C仅依赖于β1,β2,γ1,γ2,n,pi,R0,R1和|Ω|,并且ε和C(ε)分别代表Young不等式较小和较大的常数.证明过程中的常数C在不同的地方取值不同,是可以线性变化的. 证设(Ω)是方程(1.1)的-障碍问题的弱解,且0≤R0<τ 又因(Ω),ϕ ∈C∞0(BR1),于是 在Ω中几乎处处成立,从而有(Ω).由v的假设可得 注意到,对任何给定的常数k >0,当u ≤k时有v=u. 一方面, 另外一方面, 结合(1.5),(3.2),(3.3)和(3.4)式得 现在我们分别来估计(3.5)式的左右两边. 首先,由(1.2)式和ϕ=1在Bτ里成立,所以(3.5)式的左侧可估计为 下面,我们来估计I1,I2,I3. 先估计|I1|式,使用(1.3)式有, 在本文中,因为R1<1,所以|t −τ|<1,|t −τ|−pi≤|t −τ|−p(pi>1,i=1,2,··· ,n).利用Hlder不等式,Young不等式得到, 注由于pi,pj的下角标i,j代表的都是从1到n的正整数,为了与(3.6)式符号统一,故把(3.8)式第二行和第三行的第二个积分中关于j的求和改为关于i的求和. 再估计|I2|式,使用(1.3)式,(3.1)式,Hlder不等式有 为了与(3.6)、(3.8)式符号统一,故把(3.9)式最后一行的第二个积分关于j的求和也改为关于i的求和,关于|I3|的估计也使用了类似的方法.再利用Young不等式,得到 最后估计|I3|式,使用(1.4)式,Hlder不等式有 利用基本不等式(a1+a2+···+an)r≤2r(ar1+ar2+···+arn),其中ai(i=1,2,··· ,n)非负,得到 回顾前面的假设q ≤α 联立(3.6),(3.8),(3.10),(3.13)和(3.14)式,最后可得 因为ε′与ε相互独立,选择足够小的正数ε,使得θ=C(p,n,β1,β2,γ1,γ2,ε′)ε<1,则通过引理2.1 可知,对任意的R0<ρ 由引理2.2得到定理.




3.定理的证明