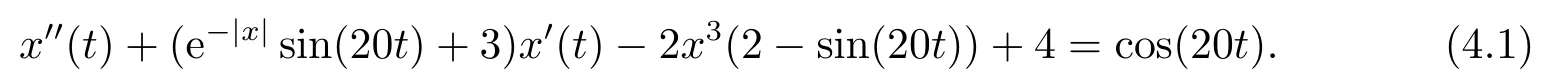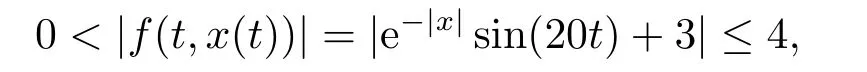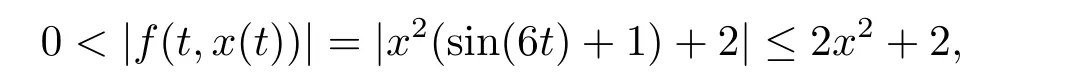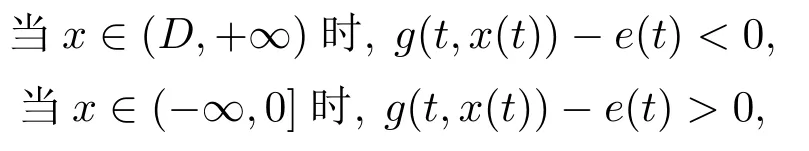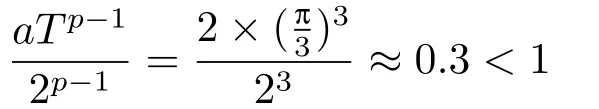一类广义Linard方程周期正解的存在性
2019-06-27崔笑笑程志波姚绍文
崔笑笑,程志波,姚绍文
( 河南理工大学数学与信息科学学院,河南 焦作454000)
1.引言

作为一个简化模型出现在科学和工程的许多领域,由于它可以用来模拟振荡电路或者简单的钟摆运动,在20世纪上半叶,人们对它进行了深入的研究.例如,Van der Pol 振荡器

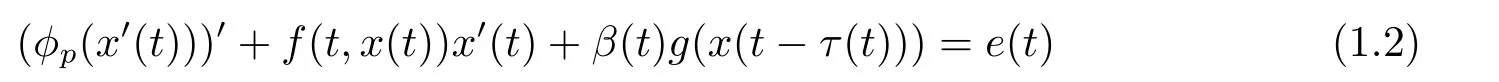
的周期解的存在性,其中自治函数g(x)满足半线性条件
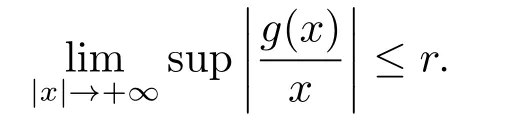

证明了方程(1.3)存在一个周期解.
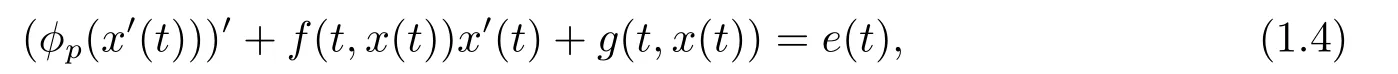
其中ϕp(s)=|s|p−2s,p ≥2是常数,f,g ∈C(R×R,R)是关于第一个变量t的T-周期函数,e(t)∈C(R,R)是一个T-周期函数.利用Mansevich-Mawhin连续定理,我们给出了下面的结论.
定理1.1假设下列条件成立:
(H1) 存在正常数a和b,使得对一切(t,x)∈[0,T]×R,有0<|f(t,x)|≤a|x|p−2+b;
(H2) 存在正常数D,使得对一切(t,x)∈[0,T]×(D,+∞),有g(t,x)−e(t)<0,并且对一切(t,x)∈[0,T]×(−∞,0],有g(t,x)−e(t)>0.则方程(1.4)在下列一种条件下至少有一个T-周期正解,
(I)p=2,且
(II)p>2,且
注1.1本文与文[4]有很大的不同.方程(1.2) 中自治函数g(x)满足半线性条件,而方程(1.4)中非自治函数g(t,x)仅仅只需要满足条件(H2),这也就是说,g可以满足次线性条件,半线性条件和超线性条件.因此本文的结论改进和扩展了文[4]的结论.
注1.2与方程(1.3)相比,方程(1.4)中的摩擦系数由f(x)变为了f(t,x),摩擦项的积分在估计方程周期解的先验界时难度大大增加,所以文[7]中的方法不再适用,这就要求我们需要寻找其他方法克服这一困难.在这里还需要特别说明的是,当f(t,x(t))≡f(x(t))时,方程(1.4)转化成了方程(1.3),文[7]是本文的一个特例.
作为定理1.1的应用,我们能得到下面的推论.
推论1.1假设条件(H2)成立,方程(1.3)至少有一个T-周期正解.
注1.3本文证明的是方程(1.4)周期正解的存在性,而文[4,7]中仅仅证明的是周期解的存在性,因此本文是对文[4,7]进一步的深入研究.
随后,我们研究方程(1.1)周期解的全局渐近稳定性.设

定理1.2假设f(0)=0,g(0)=0成立,更进一步假设下列条件成立:
(H3) 存在正常数D1,D2,使得对一切x ∈(−∞,−D1),有g(x)<0,并且对一切x ∈(D2,+∞),有g(x)>0;
(H4) 存在正常数c和d,使得对一切x ∈R,有|g(x)|≤c|x|+d;
(H5) 对一切x ∈R,有g(x)≥x;
(H6) 对一切x ∈R,有xF(x)>0.则如果方程(1.1)有唯一全局渐近稳定的周期解x∗(t)=0.
2.主要结论
首先考虑方程(1.4)的同伦方程
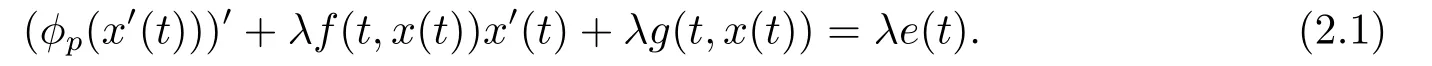
为了方便表示,我们定义
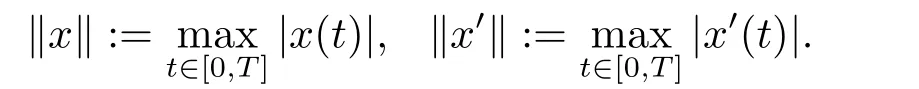
引理2.1假设存在常数E1,E2使得下列条件成立:
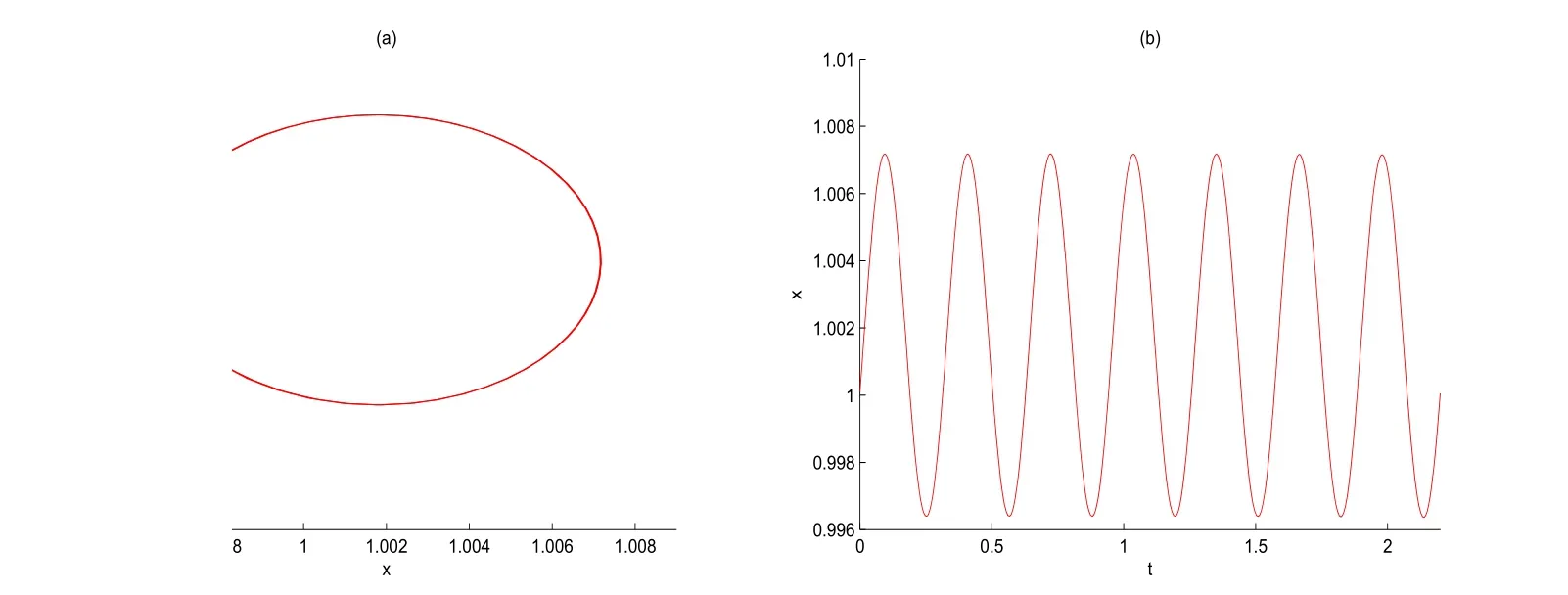
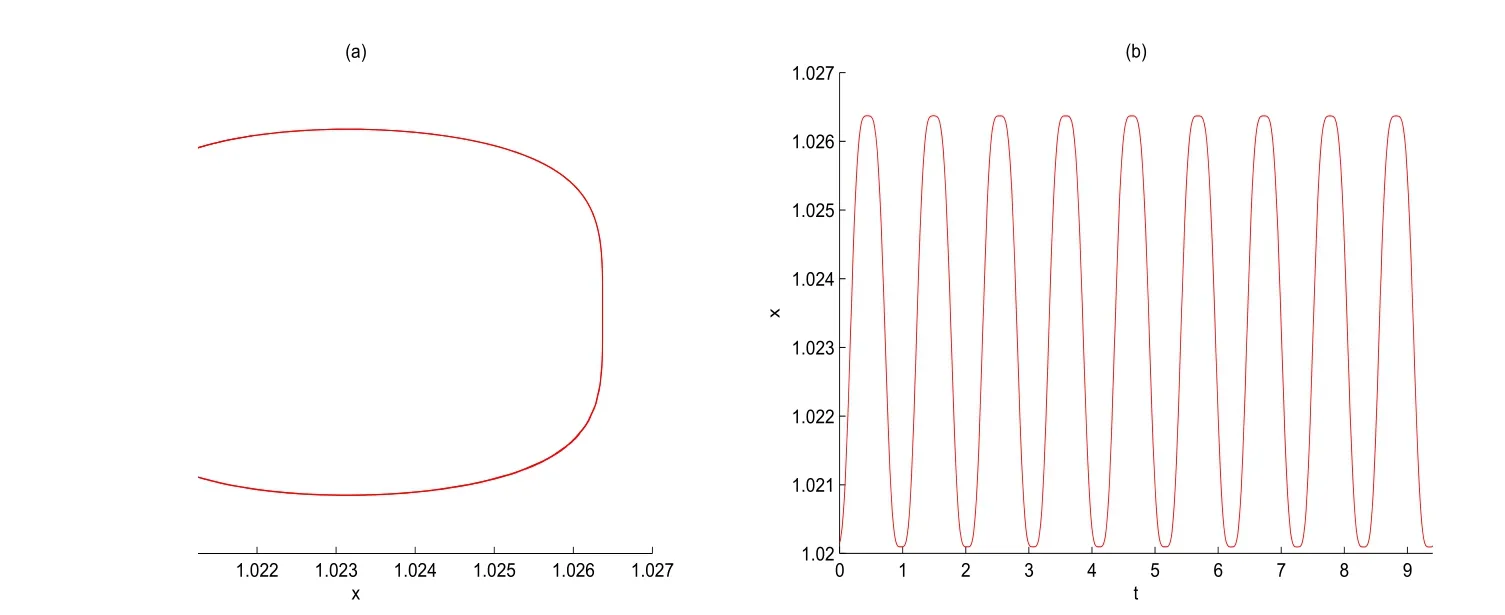
(i)对于方程(2.1)的每一个解x(t)都有∥x∥ (ii)对于方程 的每一个解C都满足|C| (iii) 则方程(1.4)至少有一个T-周期解. 接下来,我们证明方程(1.4)至少有一个T-周期正解. 对定理1.1的证明首先,我们断言方程(2.1)的所有可能的解都是有界的.令x(t)∈C1T是方程(2.1)的任意一个T-周期解. 我们断言存在ξ ∈[0,T],使得 则 令t3,t4∈(0,T)分别是ϕp(x′(t))的极大值点,极小值点,则 且 那么 把t3代入方程(2.1)得 因为(ϕp(x′(t3)))′=0,方程(2.3)化为 由条件(H1) 可知f(t,x)不变号,不妨设f(t3,x(t3))>0,又x′(t3)≥0,由方程(2.4), 由条件(H2),我们可得 同理可得 (i)若x(t3)∈(0,D),令ξ=t3,则|x(ξ)| (ii)若x(t3)∈[D,+∞),由方程(2.5) 及x(t) 关于t的连续性,存在常数ξ且x(ξ)∈[x(t4),x(t3)],使得|x(ξ)|=D.这就证明了方程(2.2).接着我们有 并且 结合上面两个不等式,我们得到 对方程(2.1)左右两边同时乘以x(t)并且在[0,T]上积分,我们得到 设G1:={x ≤0,t ∈R},G2:={0< x ≤D,t ∈R},G3:={x > D,t ∈R},则方程(2.8)可化为 由条件(H2),我们有 则方程(2.9)可化为 下面介绍一个经典的不等式,存在只依赖于p的常数k(p)>0 使得 接下来,我们考虑下面的两种情况. (I) 若p=2,则q=2,把p=2,q=2代入方程(2.13)可得 (II) 若p >2,则由方程(2.13) 很容易地看出当时,有界,同(I),存在常数使得 由方程(2.6)和方程(2.16)可得 令M1=max{M11,M12},则 因为x(0)=x(T),所以存在一点t5∈(0,T)使得 则我们可得 事实上,假设x′(t)无界,那么一定存在正常数M′′2,使得对某些x′(t)有∥x′∥>M′′2成立,那么我们有∥ϕp(x′)∥=∥x′∥p−1≥(M′′2)p−1,这与方程(2.18)矛盾,所以方程(2.19)成立. 令E1>M1,E2>M2为常数,从方程(2.17)和方程(2.19)能得到对于方程(2.1)的每一个解x(t)都有 所以引理2.1的条件(i)成立. 由条件(H2),对于方程 的每一个解C都满足 所以引理2.1的条件(ii)成立. 从方程(2.15)我们知道E1>D,−E1<0.所以从条件(H2)我们能得到 所以引理2.1的条件(iii)成立. 假设x(t)是方程(1.4)的一个T-周期解,令是x(t)在[0,T]上的最小值点,那么 并且我们能得到 由条件(H2),有 因此对一切t ∈R,有 这说明方程(1.4)至少有一个T-周期正解. 定义3.1如果x∗(t)是方程(1.1)的一个周期解,x(t)是方程(1.1)的任意一个解并且满足 那我们称x∗(t)是全局渐进稳定的. 对定理1.2的证明步1 考虑方程(1.1)周期解的存在性. 首先对方程(1.1)的同伦方程 两边同时在[0,T]上积分并化简得 由积分中值定理,存在一点η ∈(0,T)使得 由条件(H3)可知, 令D∗=max{D1,D2},则 由方程(2.6)可得 对方程(3.1)左右两边同时乘以x(t)并且在[0,T]上积分并化简可得 由条件(H4),方程(3.3)化为 余下对周期解x∗(t)的存在性证明与定理1.1的证明过程类似,此处省略. 步2 考虑方程(1.1)的周期解x∗(t)是全局渐近稳定的. 方程(1.1)可转化为方程组 其中 由f(0)=0,g(0)=0 可知x∗(t)=0 是方程(1.1)唯一的周期解,即x∗(t)=(0,0)T是系统(3.5)唯一的周期解,设x(t)=(x1(t),x2(t))T是系统(3.5)的任意一个解.对系统(3.5),我们选择形如下式的李雅普诺夫函数, 由条件(H5)和(H6),V(x1,x2)沿着系统(3.5)轨线的全导数为 由Barbalat 引理[16]可知, 即 自此定理1.2得证. 接下来,通过例子,相图和时间序列图来阐明我们的定理. 例4.1考虑下面的二阶广义Linard方程 对比方程(4.1)和方程(1.4)可知,f(t,x(t))=e−|x|sin(20t)+3,并且满足 即满足条件(H1),其中 取D=2,可以得到 即满足条件(H2).接下来我们验证条件 图4.1 -周期解对应的相图及时间序列图: (a)初始值为(1,0.103331)的-周期解的相图; (b)-周期解的时间序列图 成立.因此,通过定理2.1可得方程(4.1)至少有一个-周期正解. 例4.2考虑下面的p-Laplacian广义Linard方程 这里我们取p=4.对比方程(4.2)和方程(1.4)可知,f(t,x(t))=x2(sin(6t)+1)+2,并且满足 即满足条件(H1),其中a=2,b=2.g(t,x(t))=−x3(cos(6t)+2)+2,e(t)=cos(6t), 取D=2,可以得到 即满足条件(H2).接下来我们验证条件 图4.2 -周期解对应的相图及时间序列图: (a)初始值为(1.0236,0.04985)的 -周期解的相图; (b)-周期解的时间序列图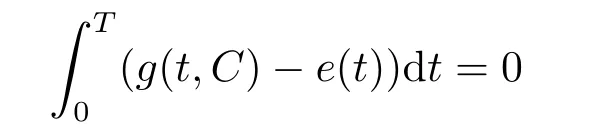


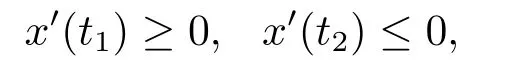

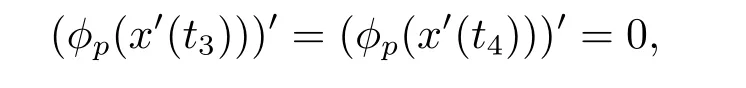

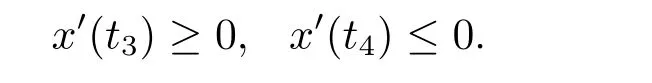

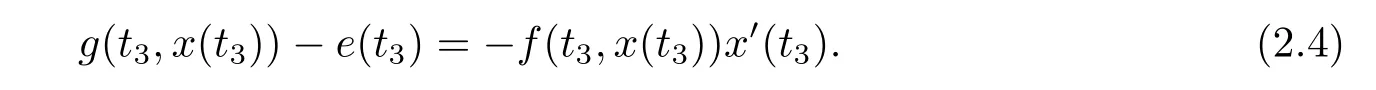
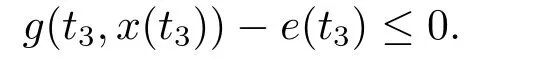
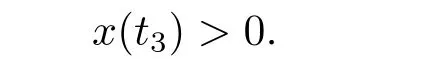
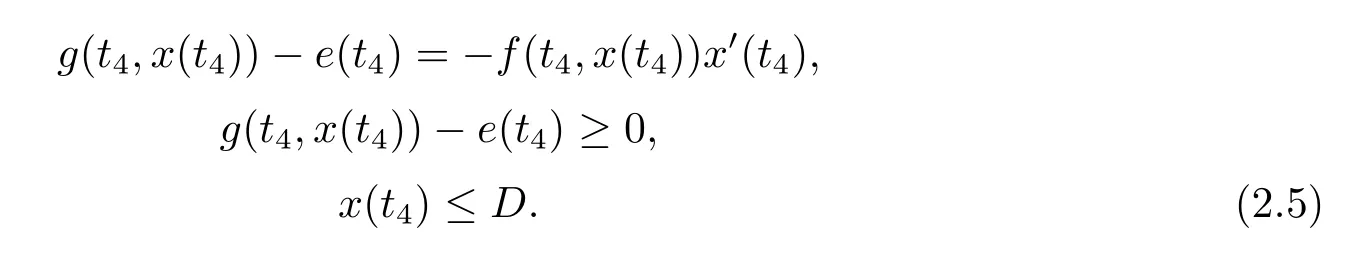
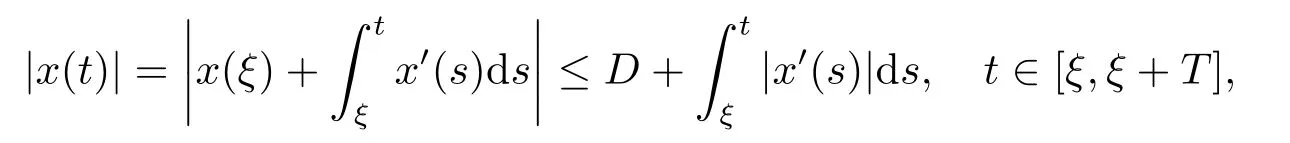
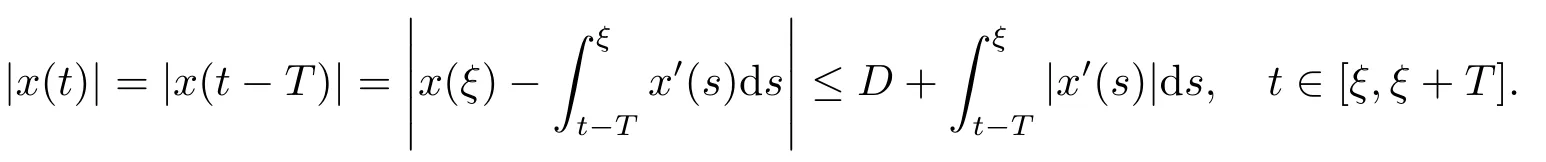
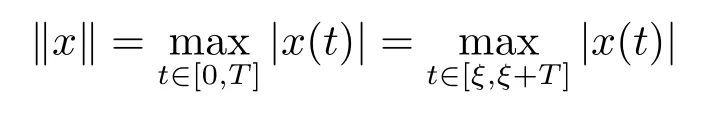

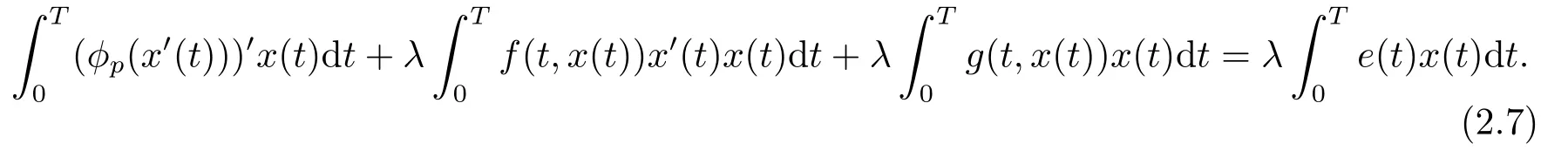


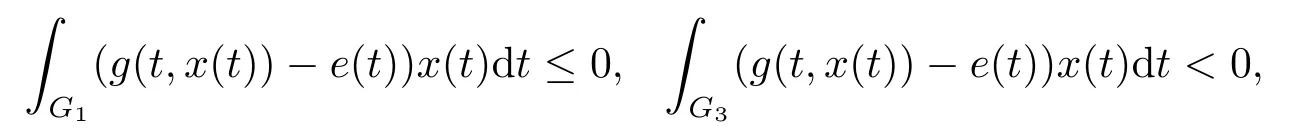
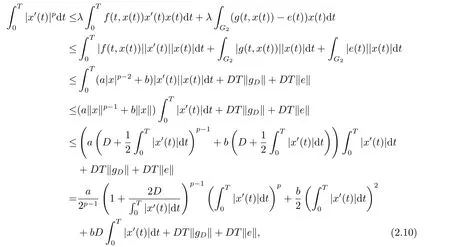
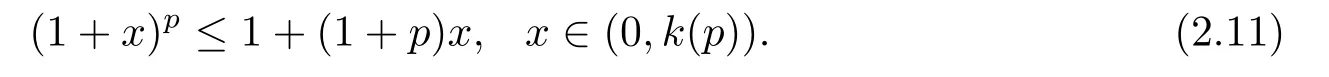

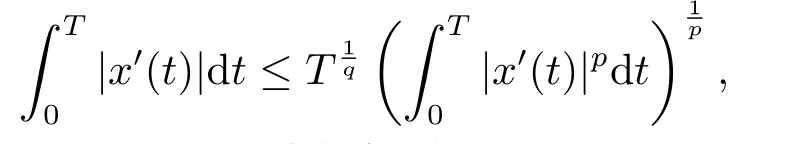
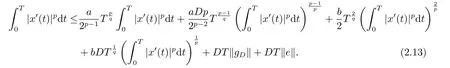



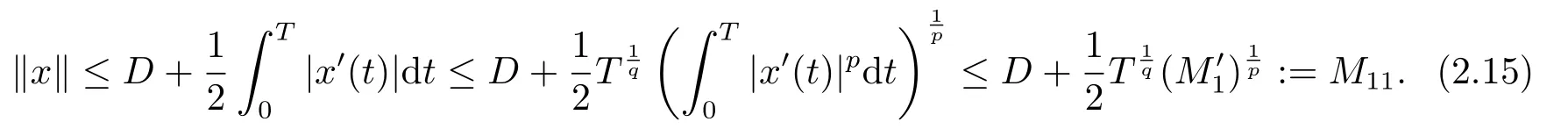






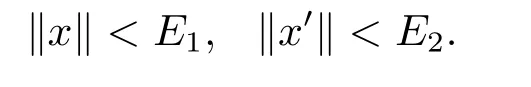





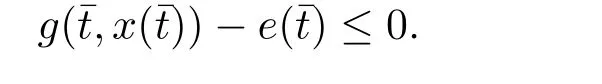
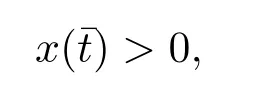
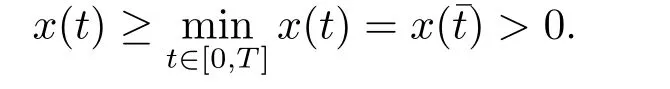
3.周期解的渐近稳定性
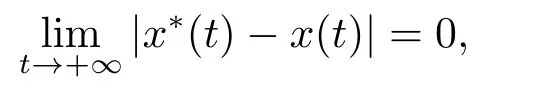

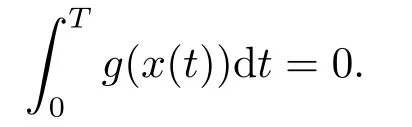
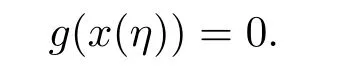

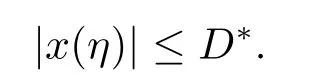

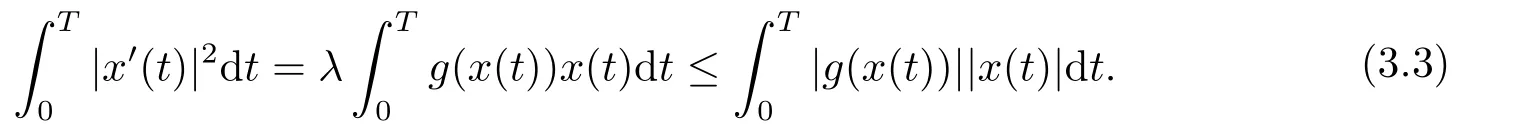
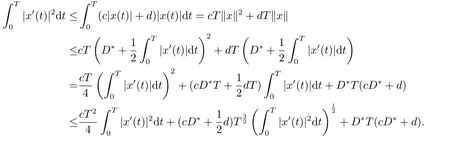

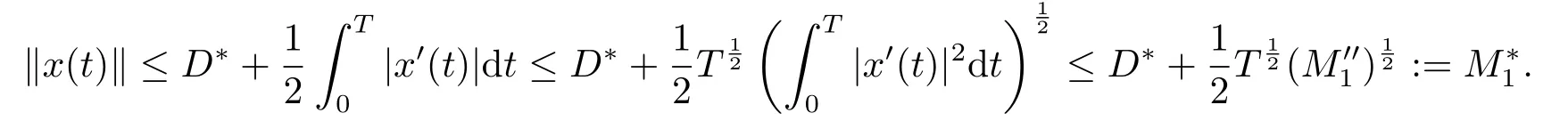

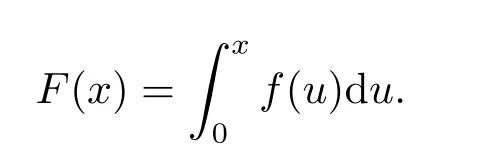



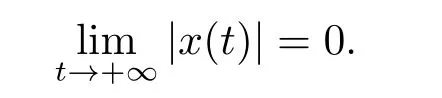
4.例子