自由落体贯入试验获得土体强度的简化分析

孟醒，王栋

(中国海洋大学 环境科学与工程学院，青岛 266100)

近年来，石油、天然气和风电等海洋资源的开发吸引了越来越多的关注。在复杂的海洋环境中获得海底土样不仅成本高昂，而且取样和运输过程中扰动严重，确定地层分布及沉积物的力学性质要求更先进的技术。与传统“取样-室内试验”相比，原位测试技术能快速准确地测定沉积物力学参数，在海洋岩土工程中具有良好的应用前景。常用的海洋黏性土原位强度测试方法包括：1)十字板法，该方法设备简单，便于应用，但每次只能量测一个深度处的不排水抗剪强度，且量测结果受扭剪速率影响较大。2)静力触探，该方法是海洋工程中应用最广泛的原位测试手段，能获得黏性土不排水强度随深度的连续变化，但设备安装耗时长，海上操作费用高。

自由下落式贯入仪(Free-Fall Penetrometer，FFP)是一种在静力触探基础上发展起来的新型海上原位仪器，依靠在自由下落过程中获得的动能，贯入仪以一定的初始速度接触黏性土海床表面，然后在阻力作用下速度逐渐降低直至为0。通过在FFP上安置加速度传感器，可量测贯入仪在水中下落及土中贯入的实时加速度，通过求解运动方程，推算海床土的不排水强度[1]。与传统的静力触探相比，FFP具有结构轻便、操作方法简单及经济性好等优点[2]，在海洋作业中已有少量应用[3]。虽然与测定土体液塑限的落锥几何外形相似，但FFP一般不用作土样的单元试验，进行室内模型试验是为了总结FFP贯入过程规律。FFP贯入速度快、动力贯入机制复杂，导致其数据解释还存在较大的不确定性。现有的研究多借助土工离心机试验[6]及常规重力条件下的模型试验[9]，变化土体的不排水抗剪强度、FFP的几何形状与重量、初始贯入速度等，研究FFP在沉积物中的实时贯入速度与埋深。对应的理论讨论多集中在土体不排水强度的率相关特性与贯入深度之间的关系。O’Loughlin等[6]曾提出动力贯入锚的简化分析模型，动力贯入锚的形状和工作机理与FFP相似，因而简化分析模型也可用于研究FFP的工作性能。

笔者进行FFP室内缩比尺模型试验，同时改进现有的简化分析模型，通过对比预测结果与试验结果验证简化分析模型的合理性，并进行变动参数计算，针对海底浅层典型黏土的不排水抗剪强度分布，提出“FFP质量-贯入速度”等值图，在已知FFP质量、贯入速度与贯入深度条件下，能够快速估计试验场地不排水抗剪强度的大致范围。

1 试验材料与方法

1.1 土样制备与FFP模型

室内模型试验所用土样为商品高岭土，塑限为37%，液限为61%，三轴压缩试验测得有效内摩擦角为24.6°，单向压缩试验得到应力水平20～50 kPa下的固结系数为11 m2/a。将白色的高岭土粉末与水混合均匀，制成1.2倍液限含水率的泥浆，然后将泥浆移入高800 mm、直径600 mm的圆柱形模型箱中。模型箱底部铺设50 mm厚排水砂层并设置排水孔，土样表面铺设排水毡层，制造双面排水条件。毡层上逐级增加配重，使得土样排水固结。先后制备3箱土样，通过改变每箱土样上的配重，制造3种典型的不排水强度随深度变化的情况：1)模型箱1，首级加载0.2 kPa，总加载5.0 kPa，加载共持续4周，土样最终高度500 mm，由于加载级数较多，并且每级加载固结时间较长，造成土样的不排水强度大致均一；2)模型箱2，首级加载0.5 kPa，总加载9.8 kPa，加载共持续2周，土样最终高度550 mm，由于加载级数较少、每级加载持续时间较短，造成的不排水强度随深度线性增加；3)模型箱3，分两个阶段固结，第1阶段首级加载0.5 kPa，总加载9.8 kPa，加载持续2周；然后在土样表面添加泥浆，第2阶段首级加载0.5 kPa，总加载5.0 kPa，加载持续1周，土样最终高度为620 mm。模型箱1和模型箱3加载过程如图1所示。当土样固结完成后，卸除全部配重，将土样表层修平。土样表面不设上覆水层，为防止水分蒸发导致强度变化，所有试验要在12 h内完成。FFP由锥尖、探杆及内置的加速度测量模块组成，如图2所示。探杆由若干200 mm长的短杆通过螺纹连接而成。短杆的数目可以自由改变，以调整探杆的长度和质量。采用两种直径的锥尖，直径D分别为10、16 mm。加速度测量模块为商品化的三轴姿态传感器，安装在工程塑料保护壳内，并通过蓝牙与电脑通讯，数据实时传输，加速度测量量程为±16g，采集频率为200 Hz。通过传感器测得初始加速度数据后，对时间积分获得FFP运动速度，再次对时间积分获得运动距离。试验整体平台如图3所示。

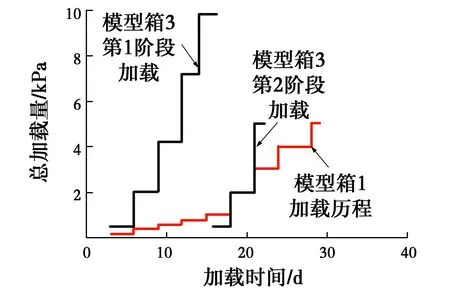
图1 模型箱1和模型箱3的加载过程Fig.1 Loading process in strong boxes 1 and 3

图2 自由下落式贯入仪模型

图3 试验贯入平台Fig.3 Experimental platform for CPT and FFP

1.2 试验安排

首先在模型箱1内进行标准静力触探CPT试验(探杆直径35.7 mm，贯入速度20 mm/s)，在模型箱2和模型箱3内进行微型CPT试验(探杆直径10 mm，贯入速度5.6 mm/s)，以获得土样的不排水强度。模型箱2内也进行了1个标准CPT试验，证明了标准和微型CPT获得的不排水强度差别不大。取锥尖阻力系数为14[11]，CPT试验结果如图4所示：模型箱1的不排水强度近似均匀，su=2.6 kPa；模型箱2，su=1.8+2.33zkPa；模型箱3的强度按多段直线表示，见图4(c)。当CPT探头接近模型箱底部时，贯入阻力突然增高是由于锥尖接近排水砂层。

FFP试验集中在研究FFP质量、初始贯入速度及土体不排水强度对贯入曲线的影响。为保证FFP在空气中垂直下落，在土体上方设置导轨，FFP由预定高度处释放后沿导轨自由下落。3个模型箱中分别进行了30个、24个以及10个贯入试验，具体试验安排如表1所示。表中列出了FFP的质量m、直径D及初始贯入速度vi。Chow等[10]报告FFP贯入导致的径向变形集中在2D范围内，本试验中规定任意两个FFP贯入点之间的间距不小于5D、FFP与CPT贯入点间隔8D以上。

表1 FFP试验安排Table 1 FFP model test program

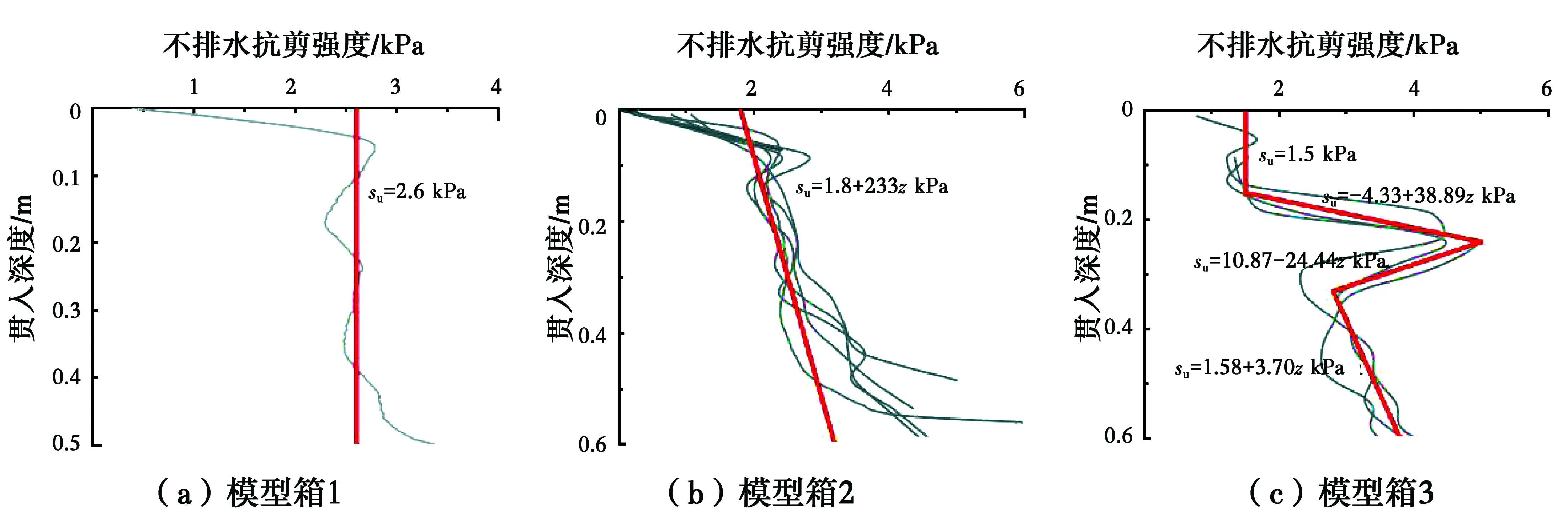
图4 实测强度曲线Fig.4 Undrained strength profiles

2 试验结果与简化分析模型

2.1 典型试验曲线

此处只展示典型的19个试验结果。图5(a)、(c)、(e)分别为模型箱1、2、3中相同质量、不同释放高度下的FFP“速度-埋深”曲线；图5(b)、(d)分别为模型箱1和2中不同FFP质量、相同释放高度所得曲线，贯入速度相同时，FFP质量越大，对应的最终贯入深度越大；图5(f)为3组模型箱中FFP质量、贯入速度均相同时的贯入曲线。所有FFP试验贯入速度范围在0～4.43 m/s，最大贯入深度326 mm，相比与制备土样厚度500～600 mm，距土样底面超过10D，可以避免边界效应的影响。试验结果符合一般规律。

2.2 简化分析模型

参考O’Loughlin等[6]提出的简化模型，分析FFP在土中的运动过程。作用在FFP上的力包括水中的自重Ws、贯入到土中后排开土受到的浮力Fb、与土体侧壁接触面积上的摩擦阻力Ffrict、锥尖受到的端阻力Fbear以及拖曳力Fd，拖曳力是贯入过程中周围被带动加速的土体反作用于FFP上的力，类似于物体在水中运动时受到的阻力。按照牛顿第二定律，任意时刻FFP的动力平衡方程为

(1)

Ffrict=αsuref_aAs

(2a)

Fbear=Ncsuref_tAp

(2b)

(2c)

式中：m′为附着在FFP上土的质量；z为锥尖贯入深度；t为时间；α为摩擦系数；Nc为承载力系数；As和Ap分别为与土接触的FFP侧壁面积和投影面积；suref_a和suref_t分别为与FFP接触的土体的平均参考强度以及FFP尖端处土体强度；Cd为拖曳系数；v为任意时刻FFP的速度。

应变率增加会导致土体不排水强度的增加，Rf为描述速率相关性的参数，某一应变率对应的不排水强度通常用式(3a)表示，其中Rf可用对数或指数形式表达，并且指数形式更适合应变速率大范围变化的问题。

su=suref·Rf

(3a)

(3b)

试验采用的FFP模型形状细长，附加质量项m′可以忽略不计[13]。O’Loughlin等提出的简化模型以动力贯入锚为研究对象，假定锚完全贯入土中(也就是锚的最终埋深大于锚长)，当锚的贯入深度超过一定临界值后，上部土体发生回流。而FFP的现场及模型试验中发现，FFP贯入深度一般不会超过自身长度，因而修正O’Loughlin等的简化模型，假定没有任何土体回流。采用Fortran语言，编程实现了式(1)的连续求解。

2.3 模型主要参数选择

式(3b)中应变速率参数β的取值一般通过反演获得，典型的β取值有0.05～0.09[15]。Low等[18]认为在速率变化数量级在10-1～102范围内时，高岭土β值的典型范围为0.03～0.08。经过大量试算，此处取β=0.07。参考应变速率(v/D)ref指标准和微型CPT试验，(v/D)ref= 0.56。摩擦系数α通常取值为土体灵敏度的倒数[19]，这实际上是假定FFP周围的土在贯入过程中被完全扰动。对于一般高岭土，灵敏度典型范围为1～3[20]，即α=0.33～1。试验中土样的固结时间最长只有4周，制备出的土样很难具备很强的结构性，因此，取α=0.7。式(2b)中的承载力系数Nc，Chung等[21]对球形建议取7～13，Chow等[10]对圆锥类似的形状取12，此处采用Nc=12。式(2c)中的拖曳力系数Cd与几何形状相关，可以通过试验[22]或数值分析[23]获得。Richardson[24]建议头部椭圆形状且长短轴长度相差较大的圆杆，Cd取0.24；当头部为圆形时，Cd增加到0.35。试验采用的FFP形状与前者形状类似，此处定为0.24。

采用显式积分法求解FFP贯入的控制方程：将整个荷载和运动过程分成一系列时间步，选用二阶中心差分法求解每一时步FFP的速度与加速度。

(4a)

(4b)

式中：变量下标表示所在的时间步。时间步长的选择是影响程序计算精度的重要因素，试算发现当步长小于10-4s时，计算结果相差极小，以下计算取步长为10-4s。

2.4 简化分析模型与试验结果比较

简化分析模型与试验结果的比较如图6所示。大部分工况中简化分析模型的预测结果与试验数据吻合较好，误差在合理的范围内，最终贯入深度zu的误差最大不超过25%。64组FFP试验中，误差在10%以内的15组，误差10～20%的42组，误差大于20%的7组。上述比较证明了简化分析模型的预测结果较为可靠。

图6 简化模型与试验结果比较Fig.6 Predicted and measured FFP velocity

3 参数分析

利用简化分析模型，既可以通过量测的贯入时程曲线和式(1)推算黏土的不排水强度分布，也可以根据场地强度的经验范围快速设计FFP试验参数。取海洋黏土灵敏度典型值2.5(α=0.4)，以得到更为普适的结论。海洋软土浅层的两种典型强度分布为：1)强度均匀。图7(a)～(c)分别为su=1、2和3 kPa时，贯入深度为1、2、3 m时对应的“FFP质量-贯入速度”。2)强度随深度线性增加，su=su0+kz，su0为表层土的强度，k为强度增长坡度。图7(d)和(e)为su0=1 kPa、k=0.8、1.2、1.4 kPa/m时，最终贯入深度为1 m和2 m时对应的“FFP质量-初始贯入速度”。由区域以往经验，大致知道浅层土的强度，根据调查要求的埋深，由图7可以快速查得需要配置的FFP质量和初始贯入速度。在实际应用时，FFP的实际贯入速度一般小于10 m/s，故图7只展示贯入速度小于12 m/s时的贯入速度。

图7 FFP“质量-初始贯入速度”曲线Fig.7 FFP “mass-initial impact velocity”

根据图7，如果要达到3 m的最终贯入深度，即使土体强度低到1 kPa时，FFP质量也需要超过10 kg，且贯入速度不能低于12 m/s。该条件在实际中不宜实现，因而FFP的贯入深度一般不能超过3 m。

4 结论

通过室内模型试验，研究了FFP在黏性土中的贯入过程，探讨FFP质量和初始贯入速度对贯入过程的影响，发现两者与FFP最终贯入深度成正比。根据FFP工作特点，发展了追踪整个贯入过程的简化分析模型。通过对比试验结果与预测结果验证了简化模型的可靠性。利用简化分析模型，可以通过量测的贯入时程曲线推算黏性土的不排水强度分布。进行了变动参数计算，以海底浅层软土两种典型强度分布为代表，给出了FFP的“质量-初始贯入速度”关系曲线，发现在实际应用中FFP贯入深度很难超过3 m。