美哉，分式的恒等变形

余中华

数学大师丘成桐说过：数学是一门很有意义、很美丽，同时也很重要的科学。从实用角度讲，数学已渗透到物理、工程、生物、化学和经济等领域，甚至与社会科学也有很密切的关系。文学的最高境界，是美的境界，而数学也具有诗歌和散文的内在气质。达到一定的境界后，我们也能体会和享受到数学之美。数学既有文学性，也有应用性，探讨它们之间妙趣横生的关系，能让人真正享受到研究数学的乐趣。

本文试通过几道分式的变形，让同学们体会数学的对称美。

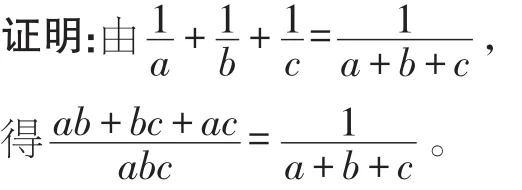
∴a2b+abc+a2c+ab2+b2c+abc+abc+bc2+ac2=abc，

∴（ab+b2+ac+bc）c+（ab+b2+ac+bc）a=0，

∴（ab+b2+ac+bc）（a+c）=0，

［b（a+b）+c（a+b）］（a+c）=0，

∴（a+b）（b+c）（a+c）=0，

∴a、b、c中至少有两个互为相反数。

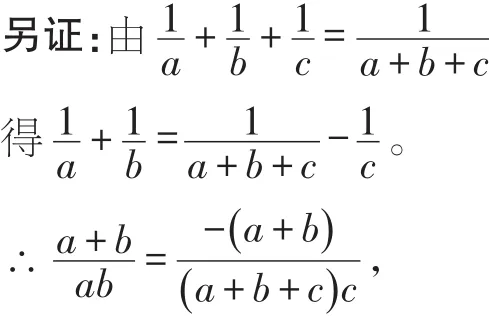
（a+b）（a+b+c）c+ab（a+b）=0。

∴（a+b）［c2+（a+b）c+ab］=0，

（a+b）（c+a）（c+b）=0，

∴a、b、c中至少有两个互为相反数。

例2 计算：

赏析：第（1）小题非常有意思，直接通分四项会非常烦琐，而前两项计算的结果正好可以与第三项运算，运算得到最终的结果。是不是有种爬楼的感觉？

第（2）题以退为进，原本分式的化简应该项数不断减少，本题反其道而行之，将四项变成八项后，反而变得更简便。生活中也是如此，以退为进有时候反而更容易达成目标。

第（3）题凑平方差公式、第（4）题裂项相消都非常巧妙，体现了数学的思维美。

赏析：本题解答过程除了体现对称美外，所用的方法也很巧妙，巧妙地取倒数，给解题者一种美妙的享受。