基于数学核心素养的初中教学探究——以同题异构课“平行四边形复习课”为例

■许凌燕

一、课例探究

1.立足学情，把握起点。

学生原有的知识和经验是教学活动的起点。任何有效的教学都始于对学生已有经验的充分挖掘和利用，这种经验包括认知经验和生活经验。

此次上课的两位教师来自不同学校，属于借班上课，因此了解学情就显得尤为重要。事实上，在两位教师得知在该校上课以后，就已经与对应班级任课教师以及班主任沟通，了解了学生的整体情况，对特殊的个体情况也有了初步的了解。在上课前一天，教师A还到对应班级与学生见面，分发学案，布置预习，相互交流。特级教师任小文曾说，我每次出去上公开课，一定会提前到班级和学生沟通几句，师生的相互了解、情感的建立是完成目标的基石。

两位教师通过精准定位学情，充分调动学生参与课堂的主动性、积极性。笔者认为正是因为备课时能从学情出发，充分考虑到学生的最近发展区，才能将数学核心素养的培养融入到整个课堂之中。

2.创设情境，梳理知识。

情境应成为学生的思维发生处、知识形成处、能力成长处、情感涵育处，创设情境就是构建课程知识内容并使之与学生的生活、经验、情感、生命相接的过程。好的情境引入能激发学生的感性思维和探究世界万物的渴望和能力。两位教师在阶段性复习课中也能注重创设情境，激发学生思维。

教师A的引入：

（1）如图1，已知四边形ABCD的周长为24cm，其中AB∥DC，AD∥BC，且AB=5cm，则BC=_______cm，AD=_______cm，CD= cm。

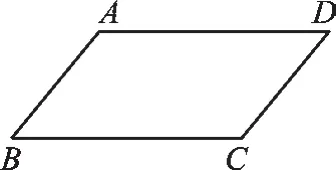
图1

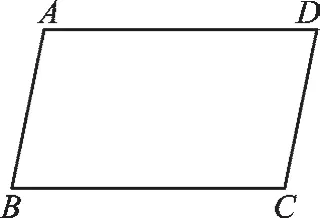
图2

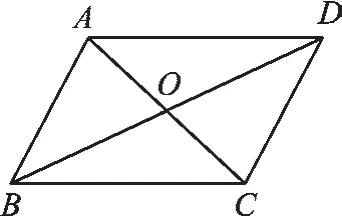
图3

（2）如图2，在 ▱ABCD 中，∠A+∠C=200°，则∠A=______°，∠D=______°。

（3）如图3，已知▱ABCD 中，AC=10cm，BD=16cm，则BC的取值范围是______。

（4）在四边形ABCD中：若AB∥CD，要使四边形ABCD是平行四边形，则需添加的条件是_____；若AD=BC，要使四边形ABCD是平行四边形，则需添加的条件是______。

教师B的引入：

如图4，你能以AB、BC为一组邻边，还原▱ABCD吗？

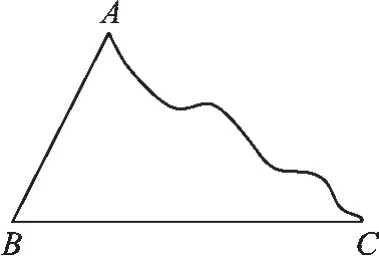
图4

两位教师的情境引入各具特点。教师A以题带知识点，激发学生回顾已有知识，构建框架结构，厘清知识脉络；教师B的引入以一个开放性的生活问题入手，让学生结合“平行四边形的判断”梳理出问题的结果，运用性强。两种不同风格的设计促使学生的认知从感性认识上升为理性认识，同时，也促进了学生形象思维和抽象思维相互转化。

3.自主探究，合作提升。

建构主义认为，学生的学习并不是一个被动接受的过程，应该在已有知识经验的基础上建构新知识，实现知识的再创造。萧伯纳曾说：“你有一个苹果，我有一个苹果，彼此交换一下，我们仍然是各有一个苹果；但你有一种思想，我有一种思想，彼此交换，我们就都有了两种思想，甚至更多。”《义务教育数学课程标准》明确要求教师引导学生独立思考，自主探索，合作交流。自主强调的是个人的主动性、积极性，渴望获得知识的一种心理特质。合作交流是自主探究的升华，是思想和智慧碰撞的途径。

教师A的探究性问题：

如图 5，在矩形 ABCD 中，AB=a cm，AD=10cm，点P在边AD上以每秒1cm的速度从点A向点D运动，点Q在BC边上，以每秒4cm的速度从点C出发，由点C运动到点B，然后立即返回向点C运动。两个点同时出发，当点Q到达点C时停止（同时点P也停止)。设运动的时间为t秒（t＞0）：（1）当t=______秒时，点Q与点C重合；（2）当点Q与点C重合时，点P运动的路程为cm；（3）在整个运动的过程中，t为何值时，四边形PDQB是平行四边形？

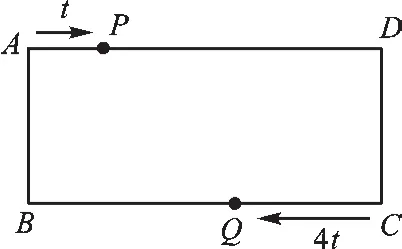
图5

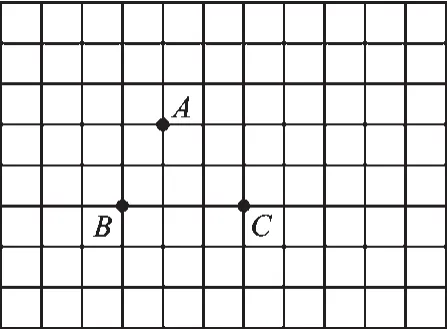
图6

教师B的探究性问题：

如图6，在边长为1的正方形网格中有A、B、C三点,请你画出以A、B、C为其中三个顶点的平行四边形。（追问：请合理建坐标系，求出顶点坐标。）

两位教师在课堂设计中都有意识地设计了探究环节。探究性问题的设计很有讲究，假如难度太大，超出学生现有知识水平，学生则无法完成探究性问题，素养的培养成为空谈；如果难度较低，在学生现有认知范畴内，探究性问题设计无效，学生没有产生智慧碰撞的火花，数学推理、数学建模能力得不到提升。上述两题型都涉及数学的分类讨论思想。教师A先展示了学生自主探究的结果，针对学生考虑不全面的情况，再要求学生合作交流，完善推理过程，同时，教师A在各个小组之间进行指导。教师B先让学生自主探究，而后小组交流展示。小组能呈现出完整分类的结果，但是在总结提炼上还欠“火候”。教师B最后给出解决此类问题的策略。

由此可见，合作交流不仅存在于学生之间，而且存在于组与组之间、师生之间。两位教师为学生营造了一个探究的场所，引导学生形成了对“平行四边形判定”的知识的“生长”。这是一种有效的“生长”，有潜力的“拔节”。

4.创新总结，提高认识。

教师在总结基础知识、基本方法、数学思想的基础上，对所学知识的必要性的阐述、研究的角度和经验的总结也是极为重要的。一个精彩的总结有益于培养学生的逻辑思维、概括能力。

教师A从基本知识点、基本图形、基本思想方法三个层面对本节课作了课堂小结；教师B从知识、思想、方法三个层面让学生做了总结（如图7）。数学教学的总结，除了总结认知层面基础知识、基本能力和基本思想方法，还应该渗透非认知层面的情感和态度，渗透一种数学情感的培养，达到“一种意识，贯穿始终”。

图7

二、基于数学核心素养的几点教学思考

1.从知识教学到素养教学，转变教学思想。

通过两节同题异构课的听、评、悟，笔者的感触是数学核心素养并非遥不可及的空洞理论，而是有具体可操作路径的。这需要教师转变教学观念，从以怎么教为核心，向以学生怎么学为中心转变，通过设计合理问题情境、实践活动等，引导学生自主探究。课堂也不再是数学训练的场所，而是引导学生“生长”的“萌发地”，让数学核心素养培养真正落地，落实到具体的数学教学过程中。

2.以数学知识本质、学生认知为起点，设计教学内容。

在初中阶段，学生认知的特点是思维的抽象逻辑性占主要优势，但还属于经验型逻辑思维阶段，在一定程度上需要感性经验的直接支持。作为一线教师，应以学生的认知水平为出发点，关注学生学习的现实起点和逻辑起点，为学生后续的数学学习提供可持续的发展空间。

例如，目前初中教学中仍有教师将一元二次方程“韦达定理”补充到教学过程中，而苏科版教材已经没有此项内容。教师往往就是将公式交代给学生，然后配以适当练习。从学生层面上来说，这已经违背其认知规律；从数学知识本质上来说，“韦达定理”并不仅仅是一元二次方程根与系数的关系，这是法国数学家韦达提出的一元n次方程根与系数的关系，其中一元二次方程仅仅是其中的一种形式而已。这种违背学生认知规律的教学使得学生“一叶障目”，产生了误区。所以，教师应加强数学知识的学习，认识数学知识的本质，这样，在教学过程中，才能更大范围地提供各种思维方式，给学生足够的思维与想象的空间，为学生更好地理解数学知识的广度与本质创设条件。

3.以有效任务为实施途径，创设问题、探究活动。

布鲁纳曾说，有效教学始于准确地知道需要达到的教学目标是什么。明确的教学目标的实现需要通过有效的活动为途径去落实，具体来说就是教师在进行教学问题、教学活动设计时，要充分考虑通过本节课的教学，可以培养或提升学生的哪些数学核心素养，这些素养可以通过哪些有效任务得以落实。例如，合理化的教学情境可以让学生体会到数学来源于生活又服务于生活，培养学生的应用意识和数学建模能力；有梯度的、有广度的、逐级深入的数学问题启发学生思考，提升学生发现问题、提出问题、解决问题的能力和逻辑推理能力；合作化的数学活动培养学生的合作意识、团队意识，使得学生在活动过程中，思维得以碰撞，使得学生与教师交流，学生之间相互交流，让学生在思考和交流中，在掌握知识技能的同时，理解知识的本质，在显性的活动中发展数学核心素养。