基于LM算法的土壤表层含水率遥感监测

许景辉 王 雷 王一琛 赵钟声 韩文霆

(1.西北农林科技大学旱区农业水土工程教育部重点实验室， 陕西杨凌 712100；2.西北农林科技大学水利与建筑工程学院, 陕西杨凌 712100；3.西北农林科技大学中国旱区节水农业研究院， 陕西杨凌 712100)

0 引言

基于无人机遥感反演的土壤含水率(Soil moisture content，SMC)监测能进行较大范围的土壤含水率测量，但目前其准确性和精度都还较低[1]。土壤表层含水率是土壤侵蚀、蒸发蒸腾及作物耗水的重要影响因素，由于距地面较浅，无法应用各类介电传感器，其自动监测一直是相关领域的难题[2]。近年来，无人机遥感技术发展迅速，基于无人机遥感的土壤含水率测量已成为国内外研究热点[1,3-9]。李小昱等[10]采用近红外光谱傅里叶变换特征提取方法检测土壤含水率，并取得了一定成果。但由于近红外光谱设备成本较高，土壤含水率相关研究的应用具有很大局限性。罗蔚然等[11]通过可见光遥感进行了土壤含水率监测，但光线的干扰使得可见光遥感精度较差。张荣标等[12]提出了中值滤波方法，但可见光影响因素众多，不能简单通过一种数学模型实现干扰信息过滤。数据挖掘技术能够很好地描述非线性模型，因此研究基于数据挖掘技术的可见光遥感技术，可有效降低成本，为无人机广域土壤含水率监测提供技术支持。

光谱的定量反演大多以线性回归模型进行，但模型训练及筛选均基于偏最小二乘回归法[5]、光谱变换[13]等简单方法。如何定量表达光谱特性和SMC的相关性、提高模型鲁棒性、降低模型过程冗杂度，仍有待优化。数据挖掘能综合考虑SMC光谱响应，降低干扰项影响，提高测量精度。数据挖掘技术中，LM神经网络是基于LM(Levenberg-Marquardt)算法的一种神经网络，其在解析非线性问题时表现能力较好，所构建模型具有很好的自适应性和鲁棒性，在建模反演中被广泛应用[14-15]。但在基于RGB颜色矩的土壤含水率监测研究应用还在探索。

本文以3种土壤(黄绵土、粘黄土、红土)为研究对象，通过野外土壤采样、室内理化分析、RGB真彩色图像采集与处理等工作，尝试采用LM神经网络构建3种土壤的可见光SMC计算模型，并对模型进行精度评定。采用BP算法[16-20]和CART算法[21-22]与之对比，比较分析3种算法在SMC监测中的效果，以实现精度高、稳定性好的无人机机载SMC测量与监测。

1 材料与方法

1.1 试验材料

选用不同类型的3 种土壤作为试验用土，分别为我国延安地区的黄绵土、陕西杨凌地区的粘黄土和江西地区红土。测得3种土壤干容重ρd为1.25、1.3、1.5 g/cm3。将3种土样晒干、粉碎并过2 mm筛网制成试验土样。分别取330 g土样装入塑料密封袋中，配成土壤含水率θ分别为0、6%、10%、14%、18%、22%的土样，密封放置24 h，使水分在土壤均匀扩散。随后将配置好的土样装入预先准备好的样品盒中(高度1.3 cm)，每种土样样品共60个。配制好后用精度为0.01 g的LT3002T型电子天平称取每一个样本的质量，供后续测量土壤样本真实含水率。

1.2 图像获取

为了调控干扰因素，便于检验模型的抗干扰性，试验在实验室内进行，采用相机(Canon EOS 500D)拍照采样，每幅图像分辨率为2 304像素×3 456像素。用三脚架固定数码相机，并调至合适高度，并保证土样置于图像中央。09：00—10：00对每种土样进行自然光线拍摄，完毕后将土壤用密封袋保存，待15:00—16:00再次拍摄完毕后，立即将样本放入干燥箱，在105℃恒温条件下干燥10 h，以获取其实际含水率。为减少偶然因素影响，每个样品取样3幅图像。为了模拟不同工作时段自然光线的影响，利用Photoshop将采集的图像进行处理，将上午样本图像亮度分别降低10%、增高15%、增高30%；下午样本图像亮度分别增高10%、降低15%、降低30%。由此，上午、下午样本各720个，土样图像样本总数为1 440个。

1.3 图像预处理与特征提取

1.3.1图像切割

图1 土样图像Fig.1 Images of soil sample

1.3.2RGB颜色矩提取

颜色矩包含各个颜色通道的一阶矩、二阶矩和三阶矩，对于一幅具有RGB颜色空间的图像，具有R、G和B 3个颜色通道，则共有9个分量。各阶颜色矩的计算公式如下[23]：

(1)一阶颜色矩

一阶颜色矩采用一阶原点矩，反映了图像的整体明暗程度，计算公式为

(1)

式中Ei——第i个颜色通道的一阶颜色矩，对应于RGB颜色空间的图像

pij——第j个像素的第i个颜色通道颜色值

(2)二阶颜色矩

二阶颜色矩采用二阶中心矩的平方根，反映了图像颜色的分布范围，计算公式为

(2)

式中si——第i个颜色通道的二阶颜色矩

(3)三阶颜色矩

三阶颜色矩采用三阶中心矩的立方根，反映了图像颜色分布的对称性，计算公式为

(3)

式中ri——第i个颜色通道的三阶颜色矩

对切割后的图像提取颜色矩，以作为图像的颜色特征。提取部分结果(红土)如表1所示。

1.4 模型构建

对提取特征值后的样本进行抽样，从各自总样本中抽取80%作为训练样本，20%作为测试样本，以检验模型的测量精度。

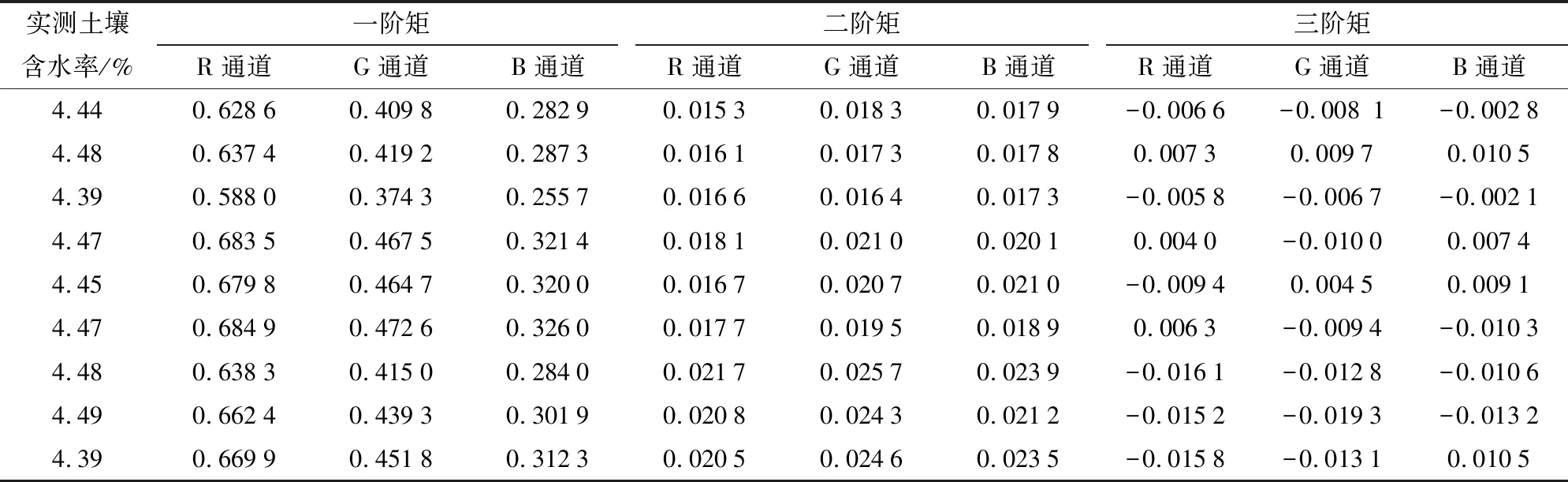
表1 土样颜色特征与相应土样实测含水率部分数据Tab.1 Partial data of soil color characteristics and measured soil moisture content of corresponding soil samples

LM算法属于二阶算法，当误差曲面的梯度较小时，LM算法类似于最速梯度法；当误差曲面的梯度较大时，LM算法类似于高斯-牛顿法[24-26]。由于LM算法能够根据Hessian矩阵估计误差曲面各个梯度方向上的学习率，与一阶算法相比，LM算法是目前训练神经网络最有效的算法[27]。LM 算法理论如下[15,28-29]：

神经网络的误差指标函数为

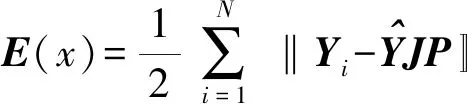
(4)

式中Yi——预期的网络输出向量

ei——当前误差

设xk为第k次迭代的网络权值向量，维数为M，牛顿算法新的权值向量xk+1为

(5)

(6)

xk+1=xk-[JT(xk)J(xk)]-1JT(xk)e(xk)=xk-H-1(xi)JT(xk)e(xk)

H=JTJ

式中J——雅可比矩阵

H——Hessian矩阵

Hk——Hessian矩阵

gk——当前梯度

然而矩阵H不一定可逆，为了解决这个问题，考虑引入系数λk，更新权值的LM算法为

xk+1=xk-[JT(xk)J(xk)+λkI]-1JT(xk)e(xk)

(7)

当λk很大时，LM算法近似于梯度下降法；当λk很小时，则是高斯-牛顿算法。

其算法流程为：①给出训练的允许误差ε，初始化权值向量x,k=0。②计算网络的输出及误差向量E(x)。③计算误差向量对网络权值的梯度值并形成雅可比矩阵。④训练完成后，更新选择。⑤如果网络收敛则停止，否则返回步骤②。

1.5 模型精度评价

为了量化基于LM神经网络、BP神经网络和CART决策树的实测土壤含水率和回归值的建模效果和性能，选用决定系数(R2)、均方根误差(RMSE)和相对分析误差(RPD)来进行模型的评价。R2越大，表明建模精度越高；RMSE越小，表明模型的预测精度越高。RPD已广泛应用于度量评估土壤属性回归模型的准确性。当RPD≥2.5时，表明模型具有极好的回归能力，当2.0≤RPD<2.5 时，表明模型具有很好的定量回归能力; 当1.8≤RPD<2.0 时，表明模型具有较好的定量回归能力；当1.4≤RPD<1.8时，表明模型具有定量回归能力；当1.0≤RPD<1.4 时，表明模型具有区别高值和低值的能力；当RPD<1.0 时，表明模型不具备回归能力[1]。

2 结果与分析

2.1 样品土壤含水率

表2为上午样本和下午样本各土壤类型SMC的统计特征。其中黄绵土的建模集与验证集所对应的均值分别是13.21%和13.12%，变异系数分别为56.18%和60.49%。而黄绵土全样本的SMC的均值为13.19%，变异系数为57.02%。可见，全样本的均值和变异系数均介于建模集和验证集之间。其他两种土样具有相同试验结果，全样本的均值和变异系数均介于建模集和验证集之间。为了验证模型对自然环境影响的适应性，除了进行上午样本和下午样本训练外，还将上午、下午样本进行混合，通过混合样本来验证模型的适应性。表3为混合样本的SMC统计特征。

2.2 土壤含水率回归模型及验证

根据各土壤实测含水率以及其相应的RGB颜色矩数据，构建基于LM神经网络、BP神经网络和CART决策树的3种回归SMC模型，分别简称为LM模型、BP模型和DT模型。各模型对于不同土壤的SMC回归结果如表4所示。表4为上午样本不同模型下土壤含水率的模型评价及回归评价结果；表5为下午样本不同模型下各土壤含水率的模型评价及回归评价结果；表6为混合样本不同模型下各土壤含水率的模型评价及回归评价结果。

由表4可以看出，LM模型的RPD值均大于2.5，而BP模型和DT模型的RPD值相对较低，但都大于1.4，因此均适合3种土壤的SMC建模。在3种算法所构建的SMC模型中，LM神经网络模型在3种土壤中均表现最佳，最佳表现土壤种类为黄绵土，模型评价参数R2为0.980、RMSE为1.0%、RPD为7.133，回归评价参数R2为0.972、RMSE为1.3%、RPD为5.964。由此可见，3种算法构建的模型回归能力由大到小为LM神经网络、BP神经网络、CART决策树，各模型对于3种土壤的适应表现能力黄绵土最强，粘黄土和红土相对较差。图2为上午样本各土壤LM模型SMC回归值与实测值。

表2 被测土壤样品SMC统计特征Tab.2 SMC statistical characteristics of sample soil samples

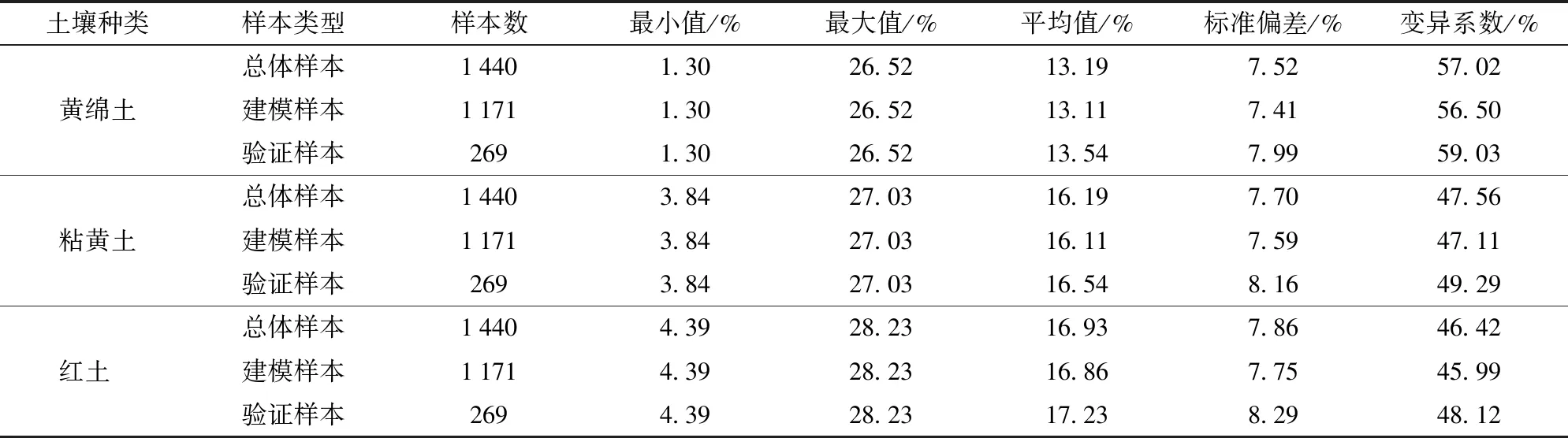
表3 混合样本土壤样品SMC统计特征Tab.3 SMC statistical characteristics of mixed sample soil samples

表4 上午样本不同模型下各土壤含水率的模型 评价及回归评价结果Tab.4 Model evaluation and prediction evaluation results of soil moisture content under different models for AM sample

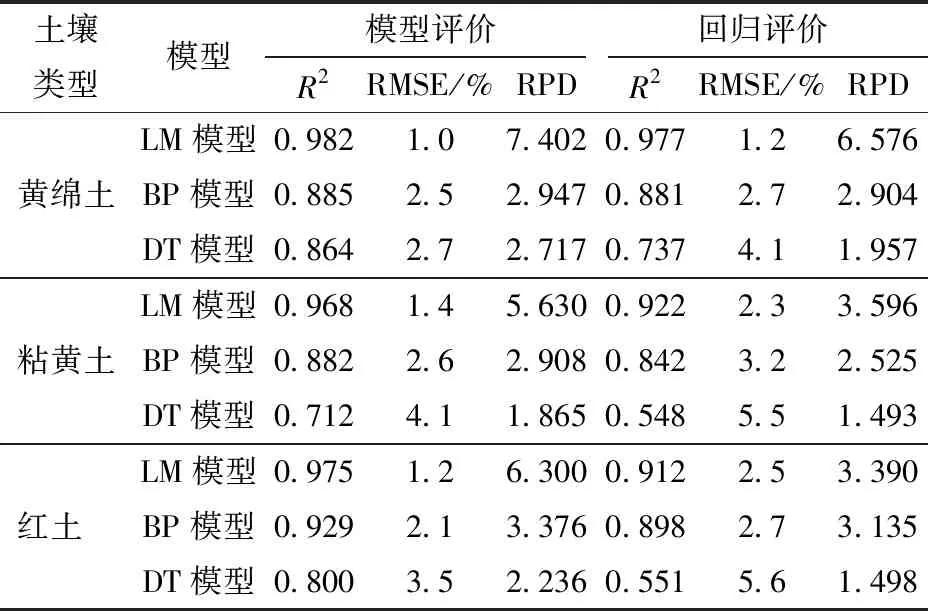
表5 下午样本不同模型下各土壤含水率的 模型评价及回归评价结果Tab.5 Model evaluation and prediction evaluation results of soil moisture content under different models for PM sample

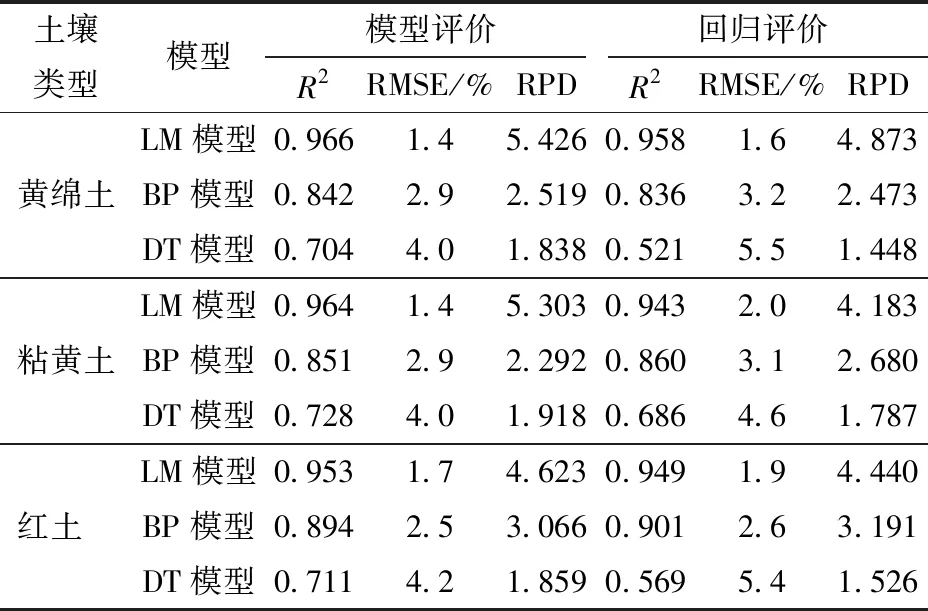
表6 混合样本不同模型下各土壤含水率的 模型评价及回归评价结果Tab.6 Model evaluation and prediction evaluation results of soil moisture content under different models of mixed samples

由表5可以看出，LM神经网络和BP神经网络模型RPD均大于2.5，适合3种土壤的SMC建模。而DT模型对于3种土壤其RPD小于2.5，尤其对于粘黄土和红土其RPD小于1.8，因此DT模型对于红土的SMC建模能力较低。同样，在3种算法所构建的SMC模型中，LM神经网络模型在3种土壤中的3个参数均表现最佳，最佳表现土壤种类为黄绵土，模型评价参数R2为0.982、RMSE为1.0%、RPD为7.402，回归评价参数R2为0.977、RMSE为1.2%、RPD为6.576。由此可见，3种算法构建的模型回归能力由大到小为LM神经网络、BP神经网络、CART决策树，各模型对于3种土壤的适应表现能力黄绵土最强，粘黄土和红土相对较差。图3为下午样本各土壤LM模型SMC回归值与实测值。

由表6可以看出，LM神经网络模型RPD大于2.5，适合3种土壤的SMC建模。而BP模型RPD值仅在黄绵土中略小于2.5，另两种土中均大于2.5，表明BP模型适用于3种土壤的SMC建模。其DT模型RPD均小于1.8，因此DT模型在混合样本中对于3种土壤的SMC建模能力较低。同样，在3种算法所构建的SMC模型中，LM神经网络模型在3种土壤中的3个参数均表现最佳，最佳表现土壤种类为黄绵土，模型评价参数R2为0.966、RMSE为1.4%、RPD为5.426，回归评价参数R2为0.958、RMSE为1.6%、RPD为4.873。由此可见，3种算法构建的模型回归能力由大到小为LM神经网络、BP神经网络、CART决策树，各模型对于3种土壤的适应表现能力黄绵土最强，粘黄土和红土相对较差。图4为混合样本各土壤LM模型SMC回归值与实测值。

图2 上午样本LM模型SMC回归值与实测值Fig.2 SMC predicted and measured values of LM model for AM sample

图3 下午样本LM模型SMC回归值与实测值Fig.3 SMC predicted and measured values of LM model for PM sample

图4 混合样本LM模型SMC回归值与实测值Fig.4 SMC predicted and measured values of LM model for mixed sample

综上所述，在SMC回归模型的建模效果和回归效果中LM模型表现最佳，BP模型回归能力相对较差，DT模型回归能力最差，因此，3种模型中LM模型回归能力和模型精度都高于其他两者，即LM模型最优，适用于土壤表层(约1 cm)的土壤水分回归。对比3种模型在各土壤的适应情况，可以看出，各模型均在黄绵土表现最佳，粘黄土和红土相对较差，可见土壤自身的颜色对于模型的回归有一定的影响。

3 讨论

研究结果表明，LM神经网络能通过大量数据训练，消除自然条件下的综合影响因素，提高基于土壤RGB颜色矩的土壤含水率识别精度。土壤可见光-RGB颜色矩与土壤含水率之间存在较好的相关性，其建模集和回归集的建模回归决定系数R2最高分别可达0.982和0.977。为通过遥感技术实现农田土壤墒情的快速检测技术提供了一定的理论基础。同时，通过对比3种算法在不同土壤类型的SMC建模回归的结果分析，得出LM神经网络建立的SMC回归模型最优，其模型决定系数R2均大于0.9。BP神经网络回归模型相对LM模型较差，DT模型相对前两种模型表现最差，在下午样本红土中其决定系数R2为0.551，基本没有回归能力。由于红土自身颜色较重，土壤含水率增加后其颜色变化敏感度较低，因此对于模型回归有一定影响，而LM算法模型能够较好地克服这一影响因素，表现了其算法的优越性。通过统计学理论分析可知，3种SMC模型在回归不同土壤含水率时，LM模型的回归效果具有较强的相关性。相较于传统线性回归模型，LM算法构建的神经网络回归模型具有显著的优越性，它不仅训练误差较小，回归能力更为精准，而且模型鲁棒性强，具有很好的非线性解译建模能力。

4 结论

(1)基于LM算法的SMC回归模型表现最优，其建模精度和回归能力最好，在下午黄绵土样本中，建模集R2为0.982、RMSE为1.0%、RPD为7.402，回归集R2为0.977、RMSE为1.2%、RPD为6.576。混合样本不同土样(黄绵土、粘黄土、红土)回归模型决定系数(R2)分别为0.958、0.943、0.949，均方根误差(RMSE)分别为1.6%、2.0%、1.9%，相对分析误差(RPD)分别为4.873、4.183、4.440。

(2)LM算法模型在黄绵土中均表现最佳，在粘黄土和红土中相对较差。由此可见，土壤自身颜色对于本研究SMC回归模型具有一定的影响。通过比较上午样本、下午样本和混合样本可知，外界光线对于LM算法的建模影响很小，说明基于LM算法的SMC回归模型具体较好的适应能力。

(3)通过分析LM模型算法建模集和回归集评价参数可知，LM算法建立的回归模型更为稳定，其回归集和建模集的决定系数(R2)均稳定在0.9以上，说明基于LM算法的SMC回归模型具有较好的稳定性。