基于K-OPLS的无线传感网络室内定位跟踪算法

李 军 后新燕

(兰州交通大学自动化与电气工程学院, 兰州 730070)

0 引言

近年来，无线传感网络(Wireless sensor networks, WSN)技术已经被广泛应用于工业控制[1]、智能家居[2]、精细农业[3]、环境感知[4]和健康监测[5]等诸多领域。同时，随着定位追踪、室内导航等室内环境下基于位置服务(Location based service, LBS)需求的日益增多，在商业区域和住宅建筑中诸如WiFi路由器等现有WiFi结构配置已被大面积使用，几乎所有的移动装置均配备了WiFi接收器。传统的定位方法是通过全球定位系统(Global positioning system, GPS)直接进行定位，由于GPS接收机能耗高，且信号容易被建筑物等阻挡，在室内环境下性能受到很大影响，因此研究无线传感网络室内定位算法很有必要。

现有的室内定位技术主要有ToA(Time of arrival)、时间差定位(Time difference of arrival, TDoA)、到达角(Angle of arrival, AoA)和基于接收信号强度指示(Received signal strength indicator, RSSI)的方法等，这些方法组合了三角测量或三边测量等技术，基于距离估计以获取未知节点的位置。与ToA、TDoA及AoA相比，基于RSSI的方法具有低功耗与无需额外装置的低成本优势，其定位方法主要包括连通性测量定位及指纹定位技术[6]。指纹定位技术不需要对网络中的通信模式做任何假设，只需在预置阶段收集所需的指纹数据库，避免了对复杂信号传输模型的直接建模，而且也无需各锚节点的确切位置，因而被广泛应用。目前，基于WiFi位置指纹定位的方法已取得许多成功应用[7-10]。

考虑到主成分分析(Principal component analysis，PCA)等特征提取技术可以有效提取原始位置指纹特征，若与现有定位算法结合，则可有效提高WSN的室内定位精度。将PCA延伸至高维特征空间，则可形成核主成分分析(Kernel principal component analysis, KPCA)算法，用于提取原始位置指纹的非线性特征，有效地挖掘数据的内在特征。文献[11]将KPCA与改进的WKNN算法结合，提高了定位准确率，降低了平均定位误差。结合PCA的优点，偏最小二乘(Partial least square, PLS)回归[12]是基于监督学习的线性回归建模算法，它充分利用输入和输出变量之间的协方差信息提取数据的潜在特征，能够有效地处理高维数据和变量间的多重共线性。文献[13]提出了一种基于隐变量正交投影(Orthogonal projections to latent structures, O-PLS)算法，该算法集成了正交信号校正的数据滤波技术，将与输出正交的内在变化从预测模型结构中分离，增强了模型的解释性。同样基于“核技巧”，将数据映射至非线性高维特征空间中，以核矩阵替换描述变量矩阵，在保留O-PLS模型框架的基础上，使得描述变量与响应变量之间存在强大的非线性映射关系，可形成K-OPLS算法， K-OPLS算法进一步改进了模型的预测性能，并已成功应用于回归与分类中[14]。

在普通最小二乘线性回归的基础上，通过加入正则项对参数进行压缩惩罚，可形成一种L2-范数正则化最小二乘回归建模技术——岭回归(Ridge regression, RR)算法，它同样可以克服变量间的多重共线性，将其延伸至非线性特征空间，可形成核岭回归(Kernel ridge regression, KRR) 算法，也称为最小二乘支持向量机(Least square support vector machine, LSSVM)，KRR在非线性建模方面也具有很好的应用潜力[6]。

鉴于K-OPLS算法在回归与分类中的应用潜力，以及SVR、KRR等核学习算法在WSN定位中的成功应用[6,9]，本文提出一种基于K-OPLS算法的室内指纹定位跟踪算法。将所提出的算法应用于仿真及实际的WiFi位置指纹定位跟踪实例中，在同等条件下，与KRR、核极限学习机(Kernel extreme learning machine, KELM)[15]、核信噪比(Kernel signal to noise ratio， KSNR)[16]、核偏最小二乘(Kernel partial least squares, KPLS)等算法以及固定预算(Fixed-budget)核递推最小二乘(Kernel recursive least-squares, KRLS)、量化核最小均方(Quantized kernel least mean square, QKLMS)两种核自适应滤波算法[17]等进行比较，以验证本文算法的有效性。

1 基于K-OPLS算法的指纹定位跟踪

假设在实验区域分布着两种传感器：锚节点以及非锚节点。锚节点具有固定的位置，记作ai,i=1,2,…,Na，其中Na表示锚节点的个数。非锚节点是可移动的且位置未知，因此需要定期定位，在给定时刻t的节点位置可记为yj(t),j=1,2,…,Ny，其中Ny表示位置未知的非锚节点数目。将K-OPLS算法应用于无线传感网络室内位置指纹定位跟踪中，具体包括两个阶段：

(1)离线阶段。在此阶段中， 以均匀或随机散布的方式在实验区域产生N个参考位置，记为yl,l=1,2,…,N，在每个参考位置布置一个节点执行测量任务，接收来自Na个锚节点发送的信号，测量来自锚节点的RSSI值，可获得N对(xl,yl)数据，从而形成位置指纹数据库，其中xl是在离线位置yl处所接收的信号功率向量，可记为

xl=(xa1,pl，xa2,pl，…，xaNa,pl)∈RNa

基于这种指纹数据库收集信息的方式，其目标是构造从向量xl与相对应的参考位置坐标之间的映射关系，第l个参考位置的第s维坐标可记为yl,s，其中s=1,2,…,D，D为空间维数，yl,s是yl=[yl,1yl,2…yl,D]T的一个元素，且满足映射关系fs(·):RNa→R，考虑D维输出的情形，其映射关系f(·):RNa→RD。若采用基于核学习的算法作为非线性逼近函数，则可以很好地构造这种映射关系。

(2)在线阶段。在此阶段中，使用离线阶段的映射关系f(·)来估计未知移动节点的位置。在t时刻，通过第j个未知的非锚节点接收来自不同锚节点的RSSI值，获取信号功率向量xj(t)，基于多维输出的映射关系j=f(xj(t))估计该移动节点的位置坐标。

K-OPLS算法应用“核技巧”处理描述变量和响应变量之间的非线性建模关系，它是O-PLS方法的非线性延伸，具有在特征空间中将模型中与结构噪声有关的预测变化进行分离建模的特性。

1.1 K-OPLS算法的模型训练

若指纹数据库中的N对(xl,yl)数据已给定，其中l=1,2,…,N，则可定义描述变量矩阵X=[x1x2…xN]T∈RN×Na与响应变量矩阵Y=[y1y2…yN]T∈RN×D，将输入数据映射至高维特征空间，即xl→φ(xl)∈RM*，则输入数据矩阵Φ(X)=[f(x1)f(x2) …f(xN)]T，核函数及相应的核矩阵可分别定义为

k(xi,xj)=f(xi)Tf(xj)K=Φ(X)Φ(X)T

按照O-PLS方法的算法实现，在K-OPLS方法的算法实现中，将以核矩阵K替换输入数据矩阵X，以对偶的形式完成。需要注意的是，K通过与Y正交的成分在算法每一步的迭代过程中完成仿射压缩。在模型训练过程中，K由两种变换后的数据矩阵实例构成，一种代表O-PLS算法中的预测权值矩阵Wp，维数为Na×D,其中D为待预测成分的数目，在整个算法实现过程中应当保留。另一种按照与Y正交的变化相应进行仿射压缩。令Kj,i表示K的不同压缩矩阵形式,其中K1,1表示原始的核矩阵K。K的第1种实例为K1,i，在计算预测得分矩阵的过程中利用了预测加权矩阵。K的第2种实例Ki,i，表示计算与Y正交的成分。Ktr,tr表示为训练核矩阵，则原始训练核矩阵中心化有

(1)

式中Itr——单位阵

Otr——元素全为1的列向量，Otr∈RN

K-OPLS模型训练步骤为：

(1) 通过特征值分解求取输出矩阵的载荷向量，可表示为

(2)

式中Y——输出矩阵，Y∈RN×D

Cp——输出载荷矩阵，Cp∈RD×D

Σp——特征值组成的对角阵，Σp∈RD×D

eigs为Matlab中的特征值分解函数，其输出结果为前D个特征值对应的特征向量及相应的对角阵。

此步骤对应于O-PLS方法对YTX进行奇异值分解。

(2)根据已知的输出载荷矩阵Cp求解Y的得分矩阵Up，即

Up=YCp

(3)

此步骤与O-PLS方法一致。

(3) 若Ao为与Y正交的成分数目，置i=1，计算第i次压缩后的预测得分矩阵，可表示为

(4)

此步骤对应于O-PLS方法中Tp=XWp，其中Tp为第i次仿射压缩后的预测得分矩阵。

(4) 计算第i个与Y正交的载荷向量，即

(5)

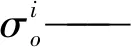
此步骤对应于O-PLS方法中对ETTp进行奇异值分解，其中E为X的残差矩阵。

(5) 计算第i个与Y正交的得分向量，即

(6)

此步骤对应于O-PLS中计算正交得分向量to，to=Xwo，wo为与输出向量正交的权值向量。

(7)

(8)

(7) 对与Y正交的变化，计算与Wp相联系的沿一个方向经第i次仿射压缩后的核矩阵，即

(9)

(8) 对与Y正交的变化，计算沿各个方向经第i次仿射压缩后的核矩阵，即

(10)

此步骤在O-PLS方法中对应于第i个与Y正交成分剔除后被压缩的X。

(9) 令i=i+1，若i≤Ao，则执行步骤(4)～(9)，否则停止压缩，并且计算所有正交向量剔除后的得分矩阵，具体可表示为

(11)

此步骤对应于O-PLS中Tp=XWp，其中X为对与Y正交的变化，依次进行仿射压缩后的矩阵。

(10) 计算所有正交向量剔除后的回归系数矩阵，即

(12)

式中Bt——Up-TP的回归系数矩阵,Bt∈RD×D

1.2 K-OPLS算法的模型测试

给定未知的非锚节点yj∈RD接收来自不同锚节点的RSSI值，可构建测试数据集(xj,yj)，j=1,2,…,Ny。因此，测试输入、输出矩阵分别为Xte=[x1x2…xNy]T∈RNy×Na，Yte=[y1y2…yNy]T∈RNy×D。定义测试-训练数据形成的核矩阵为Kte,tr，则模型测试过程的预测输出计算步骤如下：

(1) 计算测试-训练数据形成的核矩阵，即

Kte,tr=〈Φ(Xte),Φ(X)〉

(13)

其中Φ(Xte)=[f(x1)f(x2) …f(xNy)]T

(2) 对测试-训练数据核矩阵中心化，则有

(14)

式中Ote——元素全为1的列向量，Ote∈RNy

(15)

此步骤对应于O-PLS方法中计算第i次压缩后的测试预测得分矩阵Tp，其中Tp=XWp。

(4) 计算测试-训练数据核矩阵中第i个与Yte正交的得分向量，可表示为

(16)

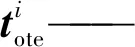
(5) 对测试数据中第i个与Yte正交的得分向量进行标准化处理，即

(17)

(18)

(6) 对与Yte正交的变化量，计算沿一个方向经第i次仿射压缩后的测试-训练数据核矩阵，即

(19)

(7) 对与Yte正交的变化量，计算沿各个方向经第i次仿射压缩后的测试-训练数据核矩阵，即

(20)

此步骤相应于O-PLS中在与Yte正交的变化方向上，依次进行仿射压缩后得到的矩阵Xte。

(8)令i=i+1，若i≤Ao，则返回至步骤(3)，否则算法终止。基于仿射压缩后的测试-训练数据核矩阵，计算更新后的预测得分矩阵，即

(21)

此步骤对应于O-PLS方法中，计算预测得分矩阵Tpte，其中Tpte=XteWp。

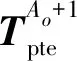
(22)

此步骤与O-PLS方法中计算预测输出一致。

2 实验

为验证K-OPLS方法的有效性，将其应用于无线传感网络室内定位跟踪中。在同等条件下，与ELM、KRR、KELM、KPLS、KSNR、近似线性依赖(ALD)-KRLS 、KLMS以及文献[17]给出的FB-KRLS及QKLMS算法等进行对比实验。不同核学习算法均选取高斯核函数

k(xi，xj)=exp(-‖xi-xj‖2/(2σ2))

(23)

式中σ——核参数

考虑到由于小波核函数具有小波信号的局部分析及对突变信号检测的多分辨分析能力，在K-OPLS方法中使用Morlet小波核函数，简记为WK-OPLS方法。小波核函数为

k(xi,xj)=(cos(ω0‖xi-xj‖)/δ)· exp(-‖xi-xj‖2/(2δ2))

(24)

式中ω0——中心频率

δ——小波伸缩因子

定位精度指标是平均估计误差，即测试点距离误差的平均值。定义实际坐标点(yl,1,yl,2)与预测坐标点(l,1,l,2)之间的估计误差为

(25)

2.1 仿真实例

仿真实验在100 m×100 m的区域内进行，均匀地在该区域内布置100个离线位置节点以及若干个锚节点，为了提高实验精度，安置在离线位置的参考节点均接收10次来自锚节点的信号，其RSSI测量值的获取使用常见的Okumura-Hata模型[18]进行计算。

Okumura-Hata模型描述了信号功率PL(dBm)与距离d(m)之间的关系

PL=P0-10αlgd+ξ

(26)

式中P0——初始功率，为150 dBm

ξ——影响RSSI测量值的噪声，ξ服从均值为0、方差为0.3的正态分布

α——路径损失指数，为4

d——锚节点与处于离线位置处的非锚节点之间的欧氏距离

实验选取高斯核函数的核参数σ=4，小波核函数的ω0=0.07，δ=12。KRR算法中，选取正则化系数λ=1×10-4，K-OPLS算法中，选取与Y正交的数目Ao=50。KELM算法中，正则化系数λ=1×10-2。QKLMS算法中，选取学习速率η=0.1，量化因子γ=0.1，当量化因子γ=0时，即为KLMS算法。ALD-KRLS算法中，最大字典容量mmax=100，阈值μ=0.01，正则化系数λ=1×10-3。FB-KRLS算法中，选取固定内存为M=300，正则化参数λ=1×10-3。KPLS算法中，选潜在变量数目为50，ELM算法中，选节点函数为Sigmoid函数，隐层神经元个数为50。KSNR算法中，正则化系数λ=1×10-9。

在不考虑噪声的情形下，图1给出了不同锚节点数目时定位跟踪精度，可以看出当锚节点数目选择为7时，实验的平均定位误差最小。图2给出了不同参考节点数目时定位跟踪精度，可以看出随着参考节点数目的增加，提高了定位跟踪精度。

若锚节点个数选择为5，首先考虑在无噪声且锚节点及节点均匀布置的情形下，生成某个特定的用于测试的轨迹，图3给出了K-OPLS算法在该区域内跟踪某移动轨迹的估计曲线，可以看出K-OPLS算法取得了不错的定位效果，显示了该算法在无线传感网络室内定位的有效性。

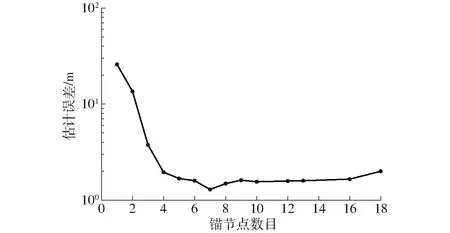
图1 估计误差与锚节点数目的关系Fig.1 Relationship between estimation error and number of anchors

图2 估计误差与参考节点数目的关系Fig.2 Relationship between estimation error and number of offline position

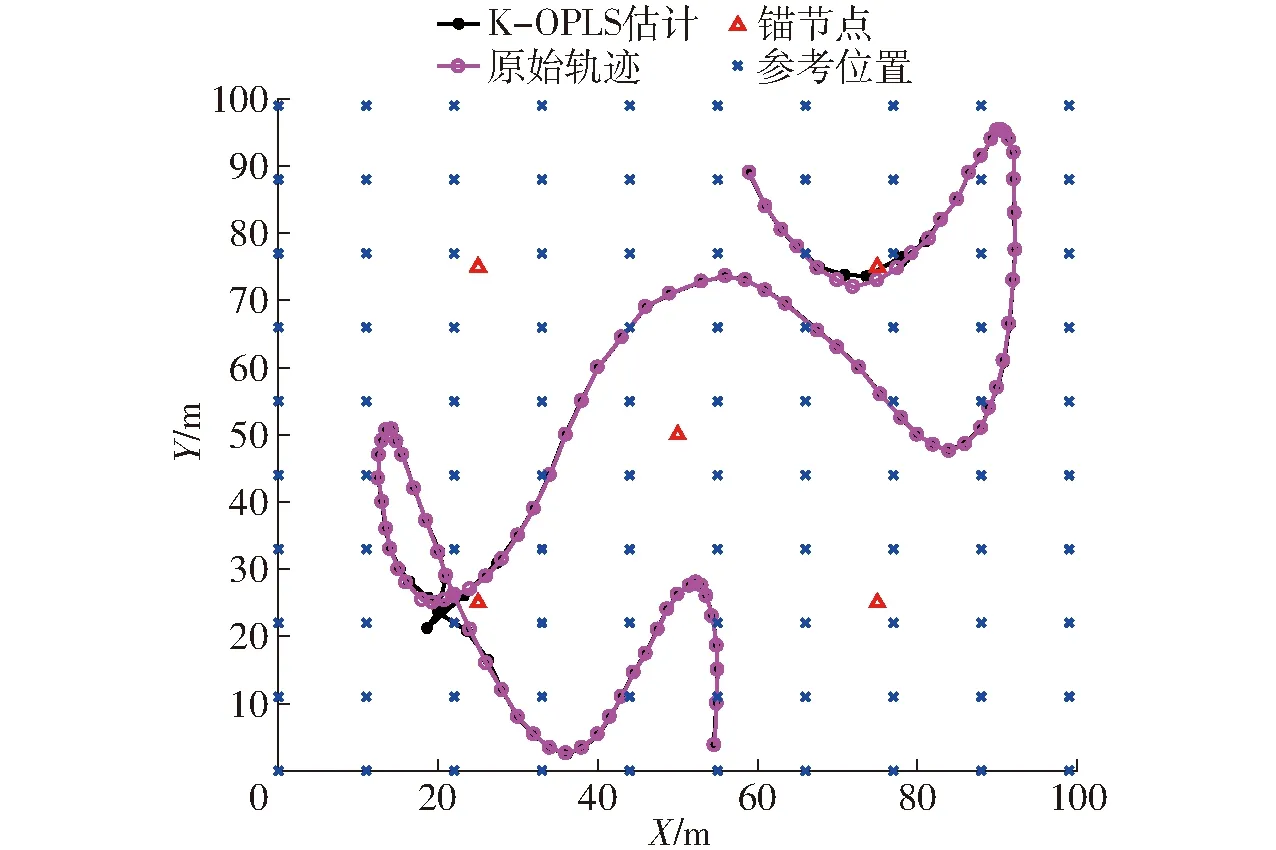
图3 无噪声环境下节点均匀分布时K-OPLS算法的 估计轨迹Fig.3 Estimation of trajectory in absence of noise under uniform distribution

在此情形下，K-OPLS算法与ELM及其他基于核学习定位算法估计跟踪误差比较如表1所示。从表1可看出，K-OPLS算法的估计误差为0.293 8 m，WK-OPLS算法的估计误差为0.232 6 m，远高于ELM算法的精度，因此，基于小波核的WK-OPLS算法具有最好的定位精度。

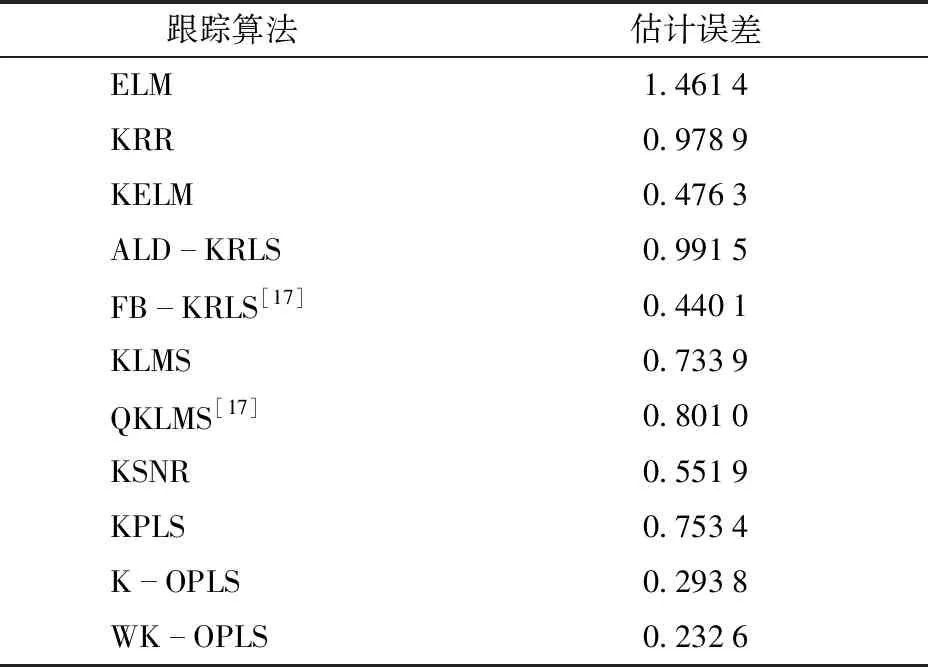
表1 无噪声时不同算法的估计误差Tab.1 Estimation error for different techniques without noise m

考虑锚节点及节点随机安置在区域内且加入标准正态分布噪声的情形，各算法的参数设置不变。在该区域内，基于K-OPLS算法跟踪某移动轨迹的估计曲线如图4所示，从图4可以看出，在含有噪声、离线位置节点随机分布情形下，K-OPLS算法同样可取得较好的定位效果。

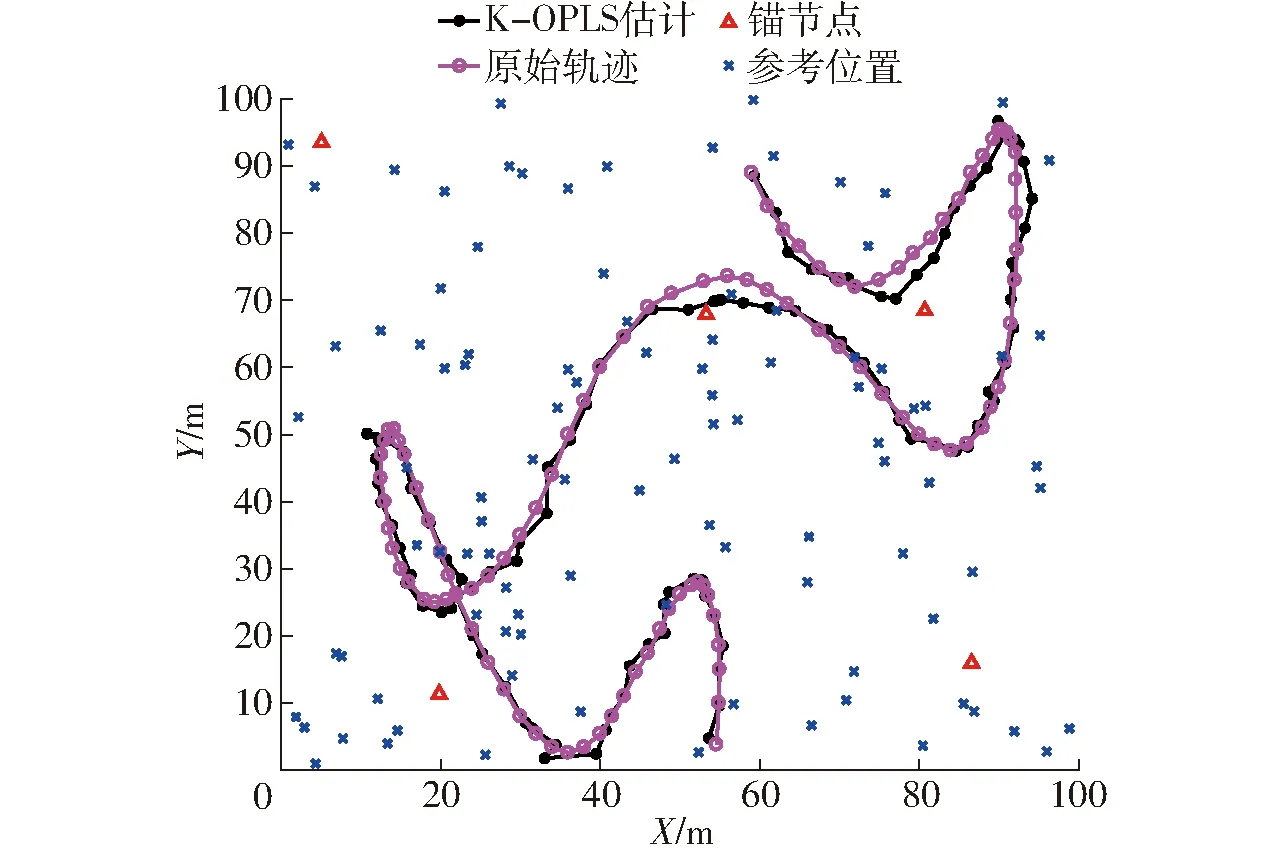
图4 噪声环境下节点随机分布时K-OPLS算法的 轨迹估计Fig.4 Estimation of trajectory in presence of noise under random distribution

考虑到在线学习算法可以实时调整模型，将QKLMS、ALD-KRLS等算法与所提出的K-OPLS算法的精度进行对比。表2给出了在噪声环境下，K-OPLS算法与ELM及其他基于核学习的定位算法轨迹跟踪时的定位误差。由表2可得，K-OPLS和WK-OPLS算法在精度上均优于其他算法，其中，K-OPLS算法的估计误差为1.322 4 m，WK-OPLS算法的估计误差为1.320 5 m，QKLMS、FB-KRLS等核自适应滤波算法由于可以对模型自适应地做出调整，它们也较适宜于时变环境下的跟踪定位。从表1、2可以看出，K-OPLS算法在精度上均优于KPLS算法，此外，同文献[17]相比，K-OPLS算法的定位精度也优于FB-KRLS与QKLMS算法，进一步验证了所提算法解释能力更强且具有一定的消除噪声能力。

表2 有噪声时不同算法估计误差Tab.2 Estimation error for different techniques with noise m

2.2 物理实例

与文献[6]一致，物理实例实验采用帕多瓦大学信息工程系SIGNET实验室所提供的实际数据集[19]，其实验在约10 m×10 m的房间内进行，在距离天花板50 cm处部署了48个均匀分布的EyesIFX节点。房间内的家具和人，会对节点所接收的RSSI值有一定干扰与影响。选择其中5个节点作为锚节点，其余43个节点被看作安置在离线位置的参考节点。为取得更好的测量结果，在该区域内通过依赖于现有节点与新位置节点之间的欧氏距离作为加权函数得到额外的57个参考节点。这使得全部的参考节点为100个。按照同样的方式产生某移动轨迹作为测试时的跟踪目标。

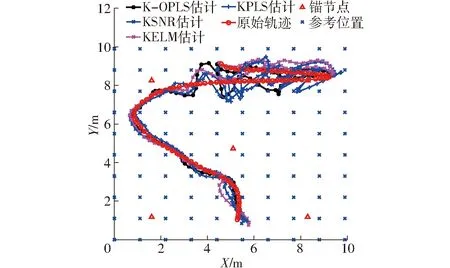
图5 实际数据K-OPLS算法的轨迹估计Fig.5 Estimation of trajectory using real data based on K-OPLS algorithm

不同算法的参数选取与2.1节实验基本一致，其中，KSNR算法中，正则化系数λ=1×10-14。小波核函数的ω0=0.05，δ=20。K-OPLS算法在该区域内跟踪某移动轨迹的估计曲线如图5所示，可以看出K-OPLS算法在真实物理环境下也能取得较好的定位效果。

表3给出了K-OPLS算法与ELM及其他基于核学习的定位算法进行轨迹跟踪时的估计误差。可以看出K-OPLS算法在精度上明显优于其他定位算法，其中WK-OPLS跟踪估计误差为0.249 3 m，此外，KSNR算法将信噪比融入到核空间中，使得该算法对于噪声具有一定的抗干扰能力，也取得了较好的跟踪效果。

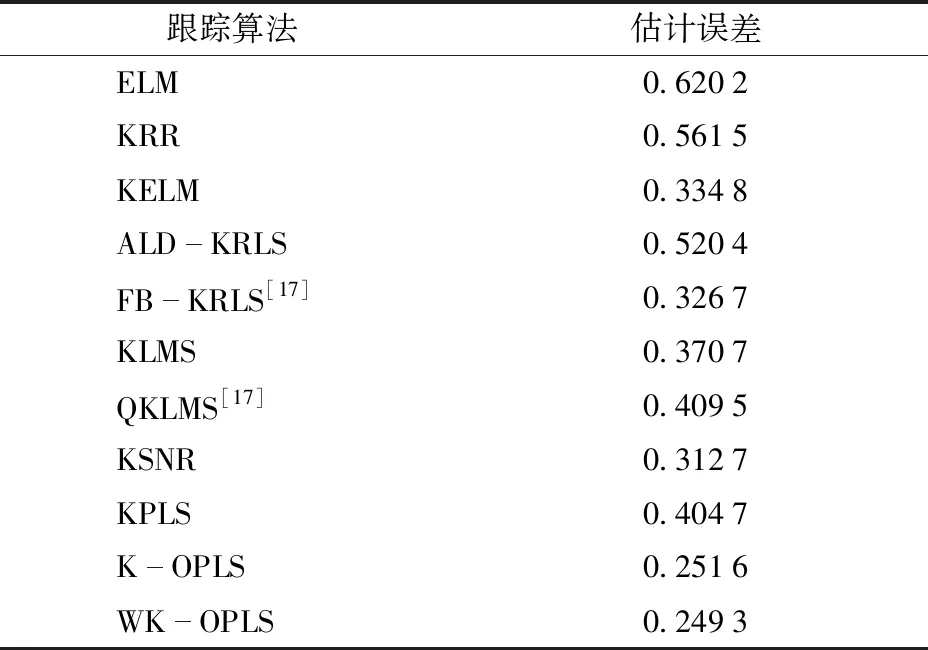
表3 真实环境下的不同算法估计误差Tab.3 Estimation error for different techniques in real environment m

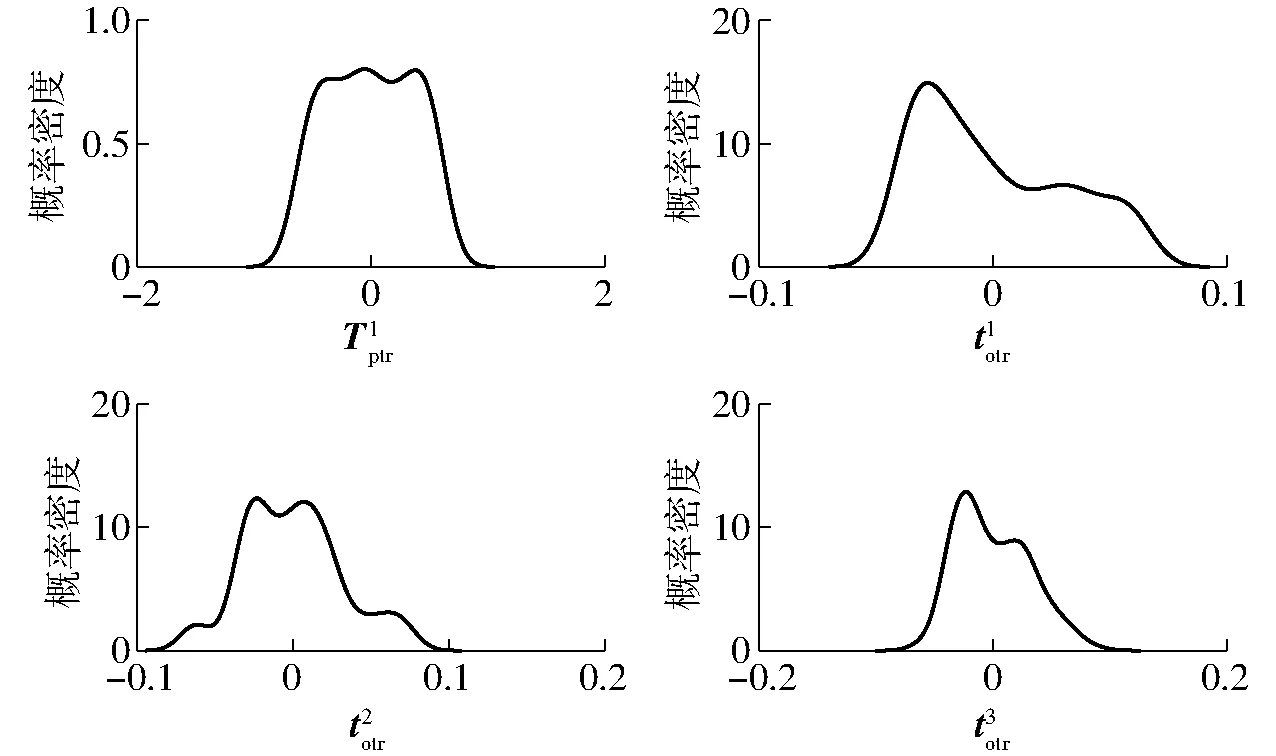
图与的概率密度函数估计Fig.6 Estimation diagrams of probability density function of

3 结论

(1)提出了基于K-OPLS的无线传感网络室内定位算法。K-OPLS算法将输入数据映射至高维特征空间中,将特征空间中与输出无关的数据剔除,因此所建立的模型更为紧凑，且模型的解释性更强。

(2)核学习算法在一定程度上提高了回归建模的非线性逼近能力，仿真和物理实例的实验验证了所提算法的有效性。K-OPLS算法相对于其他几种算法，在一定程度上克服了噪声干扰。

(3) 在定位跟踪应用中，K-OPLS算法与ELM及其他基于核学习的算法相比，不仅使得模型具有更强解释能力、更低模型复杂度及有效的滤除结构，而且其参数的调节也更为方便。