无刷直流电机SVPWM控制器的设计

王丁军，赵 涛，，朱爱华，刘汉忠，徐宏健

(1.南京工程学院 自动化学院，南京 211167；2.南京工程学院 电力工程学院，南京 211167)

0 引 言

无刷直流电机(BLDCM)具有体积小、效率高等特点，被广泛应用于汽车、计算机外围设备、家用电器等领域[1]。传统的无刷直流电机控制系统对性能的要求较低，通常采用方波控制策略实现无刷直流电机的驱动。但是，当对电机运行时的噪声和转矩脉动有较高要求时，传统的方波控制策略不再能满足要求[2]。近年来，国内外学者提出了空间矢量脉宽调制技术的概念，有效解决了传统的方波控制会给BLDCM控制系统带来载波频率过高时会有开关损耗、直流电压利用率低、低速时存在转矩脉动等一系列问题[3]。这一技术主要利用的是平均值等效原理。在任意一个调制扇区内，选定两个相邻的基本空间电压矢量分别作用一定的时间，这两个基本空间电压矢量施加到电机上的效果等同于参考电压矢量单独施加到电机上的效果。同时，为了使电机的运动轨迹近似为圆形，要求选定的两个基本空间电压矢量的作用时间具有可调性，并且可以在其交替作用过程中添加一定的零矢量来达到该目的[4-5]。

本文以BLDCM作为对象，在研究空间矢量脉宽调制原理的基础上，对基于STM32F103的BLDCM正弦波控制系统进行了设计，并进行了实验验证，结果表明: 正弦波电流驱动的BLDCM，转矩脉动减小，电机性能有所提高。

1 BLDCM的SVPWM算法研究

1.1 SVPWM矢量作用时间计算

BLDCM工作在方波控制时，采用的是两相绕组导通，每60°换相，存在绕组利用率低和换相转矩脉动的问题，而在SVPWM方式下，将功率变换器和无刷直流电机视为一个整体，目的在于使电机产生圆形磁场。功率变换器的开关方式与电机的空间电压矢量息息相关。根据文献[6]可知，变换器共有八种开关状态，分别为100，110，010，011，001，101，111和000，前6种为有效开关状态，后两种为无效开关状态。这八个状态与8个空间电压矢量U0～U7一一对应。

矢量U0和U7的振幅为零，其余6个电压矢量的振幅为2Udc/3，这6个电压矢量两两相隔60°，因而复杂的平面被划分成了6个扇区1～6，在任一扇区，均需选择两个非零电压矢量和零矢量共同作用来完成驱动无刷直流电机的任务。

为了获得连续旋转的电压矢量，定义了一个可由电压矢量U0～U7计算得来的参考电压矢量Uref。Uref位于任意一个扇区时，均可由相邻的两个非零电压矢量和零矢量合成得到，其合成公式为

(1)

式中，TPWM是开关周期，TX、TX+1、T0和T7分别为空间电压矢量UX、UX+1、U0和U7的作用时间。

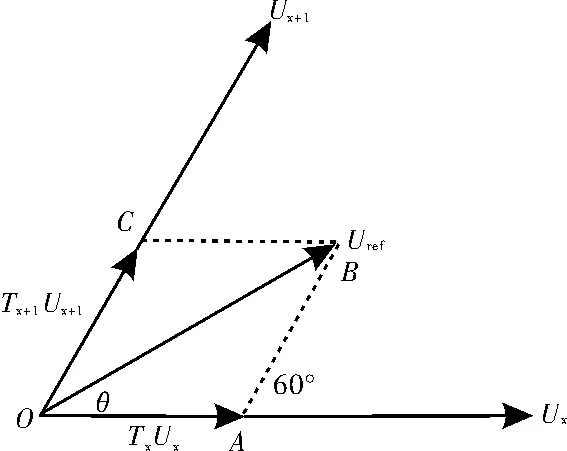
图1 空间电压矢量合成图

设图1中Uref和UX的夹角为θ，根据三角变换，可以得到如下公式

(2)

根据文献[6]可知各矢量的作用时间为

(3)

其中，TPWM为SVPWM周期，由电机控制系统本身决定；m为调制度，其值可在0～1内变化，由转速闭环控制；Udc为直流电源电压。

1.2 转子位置估算

要想计算各空间电压矢量的作用时间，关键是计算出转子在扇区内转过的电角度θ。为了保证无刷直流电机的转子和空间电压矢量同步旋转，通常利用霍尔传感器对转子进行位置估算[7]。

在无刷直流电机起动时，首先读取霍尔传感器的状态信号，通过该信号判断转子当前所处的扇区，然后以某一较小的速度控制电机转子匀速旋转。当转子转过一个电周期后，便可以计算得到转子的角速度，进而得到转子在每一个开关周期内的步进角。

θ和转速息息相关，转速为

(4)

式中，V为转子的电角速度，t为转子转过2π弧度所需要的时间。

设在2π弧度内SVPWM更新中断的次数为n，则

t=n*TPWM

(5)

设Δθ为转子的步进角，则

Δθ=TPWM*V

(6)

将式(4)、式(5)和式(6)联立方程组可以解得

(7)

而θ又为在某个扇区内，每个开关周期转子所转过的角度之和。假设转子在同一个扇区内的角速度不变，因而

θ(k+1)=θ(k)+Δθ

(8)

式中，θ(k+1)为本次运算得到的转子的相角，θ(k)为上次运算得到的转子的相角。

无刷直流电机进行换相时，由于SVPWM控制系统自身的原因，将会导致转子相角滞后，电流也会产生畸变，从而电机无法获得最大电磁转矩。为了解决这一问题，假设定子电流矢量滞后定子空间电压矢量θZ电角度，则在进行转子相角计算时应补偿θZ电角度[8]。

同时，考虑到霍尔传感器机械安装位置不准确导致扇区大小不一的问题，根据式(8)可得:

(9)

即在完成θ角的计算时，对θ是否大于60°进行判别。若θ大于60°，则跳过SVPWM算法运算，用上一次计算得到的值去更新比较寄存器，否则将进行SVPWM算法运算。

2 正弦波控制系统设计

2.1 系统结构

图2为无刷直流电机SVPWM控制系统框图，该控制系统根据霍尔信号判断转子所处扇区并计算转子转速，产生与给定控制信号相对应的SVPWM控制信号，从而控制三相全桥变换器工作，达到利用正弦波驱动无刷直流电机运行的目的。

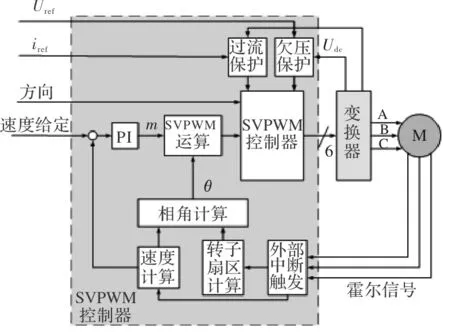
图2 直流无刷电机SVPWM控制系统框图

2.2 SVPWM控制策略

在基于STM32F103的平台上实现该算法，对SVPWM中各矢量作用时间的理论计算公式做了优化。理论公式需要以时间为单位计算出各矢量的作用时间后才可以进一步推导出定时器比较寄存器的值，而本文不以时间为单位计算，而是进行无量纲运算，直接求出比较寄存器的值，将理论计算公式中的部分浮点数运算转化为整数运算，部分乘除法运算转化为加减法运算，使得运算时间大为减少，因而可以选取较大的开关频率。

首先，定义两个变量tx和ty，其值为

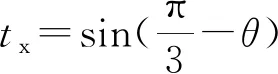
(10)

令

M=m*TPWM

(11)

这里，TPWM不以时间作为单位，而是无单位的数值，其值等于定时器周期寄存器的值。

设整型变量

(12)

TX、TY和TXY不具有实际意义，仅为获取比较寄存器装载值的中间变量。而比较寄存器装载值的具体大小还与转子所处的扇区有关。以电机正转时，转子位于第1扇区为例，定时器的3个比较寄存器的值为

(13)

其中，CCR1、CCR2和CCR3为定时器的3个比较寄存器，TPWM_2为TPWM的1/2。以此类推，可以求得转子位于其他扇区时3个比较寄存器的值。

至此，求得CCR1、CCR2和CCR3的值之后，SVPWM算法才完成了和STM32F103的融合，实现了基于STM32F103的SVPWM算法设计。

2.3 转速闭环控制策略

为了使无刷直流电机能够迅速起动达到给定的速度，且使得其具有一定的抗扰动能力，采用数字式PI控制实现速度闭环，其计算公式如下

Δu(k)=Kp[e(k)-e(k-1)]+K1e(k)

(14)

首先需要对电机的实际速度进行采样，然后与给定速度做差得到速度误差，将该速度误差代入式(14)中可以得到控制量，最后要将速度控制量转化为调制度，在SVPWM算法中利用调制度来达到控制电机速度的目的。

设电机的最大速度为Vmax，PI控制算法运算后得到的速度控制量为VC，则相应的调制度m为

1.3.4 麻醉前和术毕分别抽取静脉血5 mL，测定血清皮质醇浓度，计算患者△皮质醇浓度=麻醉前皮质醇浓度-术毕皮质醇浓度。

m=VC/Vmax

(15)

在本文中，对速度采样进行滑动窗口滤波，转子每转过一个扇区将对最旧的一个数据窗口进行更新，并计算转子平均速度。

3 实验研究与结果分析

本文选用的无刷直流电机型号为57BL55S06 230TF9，其特性参数如表1所示。

表1 57BL55S06 230TF9电机参数表

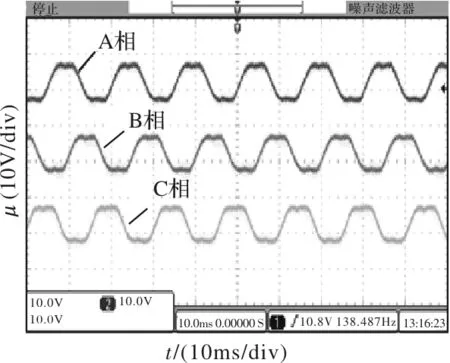
图3 SVPWM控制下反电动势波形

图3为系统稳定运行时，电机A、B、C三相反电动势的波形，从图中可以看出，反电动势波形为马鞍形波。但是马鞍形波并不是对称的，这是由于霍尔传感器安装位置的偏差导致扇区的大小不一，某些扇区的角度小于60°，某些大于60°。当电机转子位于小于60°的扇区时，转子相角还未达到60°便进行了换相，导致这个扇区内的波形相对较窄。而当电机转子位于大于60°的扇区时，转子相角早就达到60°一直在等待换相，并没有进行空间矢量脉宽调制算法运算，而是沿用最后的计算值，导致这个扇区内的波形相对较宽。

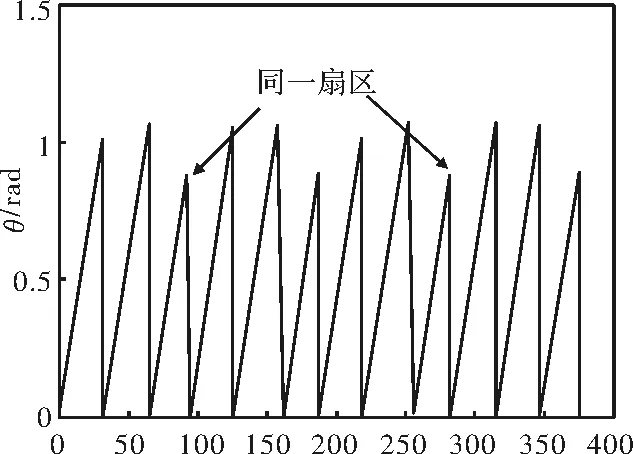
图4 值折线图

这一问题还可以通过θ的值的变化反应出来。在图4中，每个扇区内θ的峰值并不相等，均在π/3(1.05)左右摆动。在π/3以下正是由于在小于60°的扇区内，θ还未累加至60°便发生了强迫换相使得 被清零；在π/3以上是由于在大于60°的扇区内，虽然在θ大于60°时停止了空间矢量脉宽调制算法的运算，但θ的值一直在累加，直至霍尔换相信号到来时才对θ进行清零。

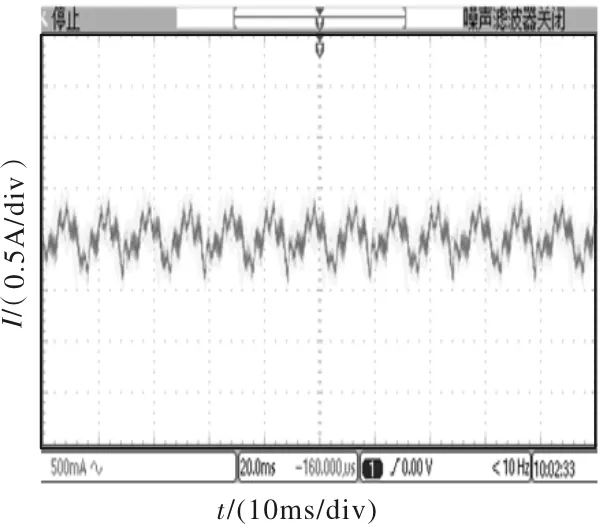
图5 未加补偿相电流波形

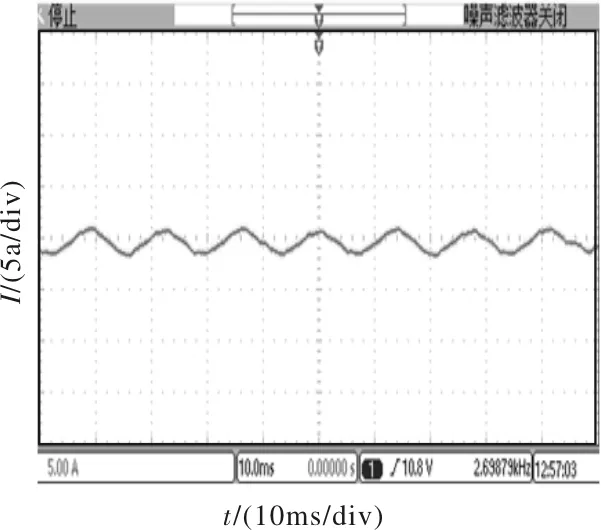
图6 加入补偿相电流波形图相电流波形图

图5为未加入相角补偿，电机稳定运行时相电流波形，该波形并不是标准的正弦波，且波形毛刺较多。经试验分析得出，定子电压空间矢量超前定子电流矢量大约11.5°，在此基础之上对转子相角进行了补偿，补偿后的相电流波形如图6所示。从图中可以看出，补偿后的相电流波形大致为正弦波，符合要求。

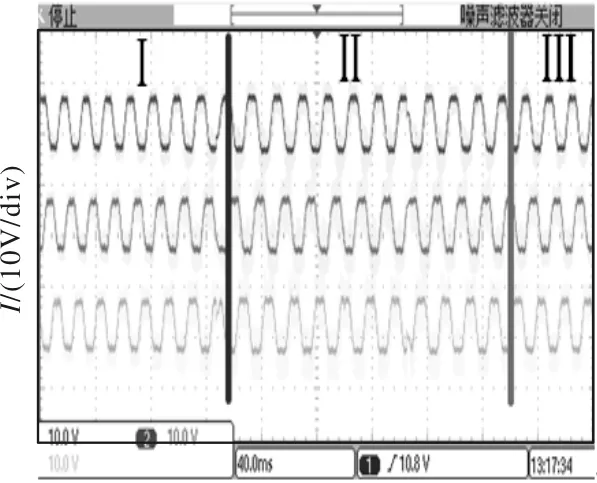
图7 带载后反电动势波形

图7为带载时电机的反电动势波形，Ⅰ区域为空载时波形，Ⅱ区域为带载时波形，该波形明显变宽，电机速度降低。经过一段时间到达Ⅲ区域后，反电动势波形再次恢复正常，与带载前的波形类似，正是由于PI调节器的作用使得电机的速度再次稳定。这不仅验证了SVPWM算法的正确性，而且验证了PI控制算法设计的正确性。

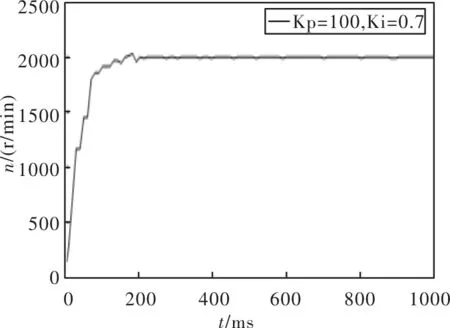
图8 KP=100，KI=0.7时速度响应曲线图

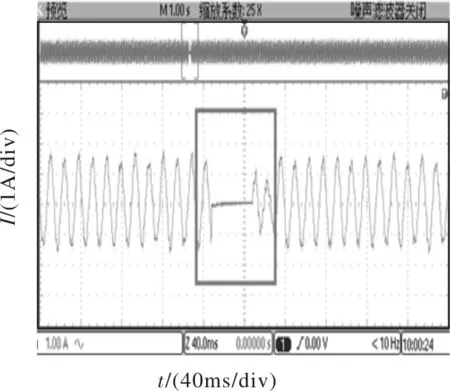
图9 堵转时电流波形

设定电流截止负反馈的阈值为0.5 A，则在电机正常运行过程中突然令电机堵转，电机立即停车，用示波器采得的电机A相电流波形如图9所示，其中方框内的波形为电机堵转时的波形。从图中可以看出，当电机出现过流故障时，控制系统立即断开控制信号，电机自然停车，电流为零。当电机过流故障解除时，控制信号自动合上，电机起动，电流逐渐上升，直至稳定。

4 结 语

本文从理论上对BLDCM的SVPWM控制方法进行了分析，实现了无刷直流电机的正弦波控制，有效减小了无刷直流电机在运行过程中的转矩脉动。通过实验证明，采用上述控制方案，电机不仅能具备良好的运行特性。而且采用采用STM32F103为主控芯片使得无刷直流电机控制系统功能全面，而且成本较低，简化了硬件的设计，为BLDCM的控制提供了一个解决方案。