压电式压力传感器温度补偿算法的研究

谭士杰,刘 凯，代 波

(1.西南科技大学 环境友好能源材料国家重点实验室，四川 绵阳 621000;2.西南应用磁学研究所，四川 绵阳 621000)

0 引言

目前广泛应用的压电式传感器具有指标性能优良，成本低及封装尺寸小的优点。然而，在应用中压电式压力传感器的工作温度稳定性会随工作环境温度的变化而出现波动，这给实际工程应用带来较大问题。从机理出发，这是由于材料本身的热膨胀系数的匹配性差造成的。温度系数会导致压电薄膜在全温变化时出现热应力，灵敏漂移度和零点漂移度均会随着温度的变化而出现一定的上升，此时，压力传感器的感应性能会随之降低，如果应用要求对于传感器的温度性能标准较严格，那么必须对压电式压力传感器进行相应的温度补偿设计。通常，补偿的方式有硬件补偿和软件补偿两种。硬件补偿技术的问题主要集中在通用性差，精度低及调试较难，由于各方面因素的影响，硬件补偿并不适用于实际的工程应用中。软件补偿技术的工程适用性比硬件补偿更大，所以，软件补偿是目前最常用的一种环境温度补偿法[1-5]。

1 研究内容及方案

本文针对灵敏温度系数及零点温度系数为线性变化的传感器开展了研究。首先对给定的常温数据进行采集，利用相关推导公式对温度变化的线性进行计算，同时也关注传感器输出和输入之间线性关系的稳定性。温度补偿对于传感器的线性关系的影响，主要是对灵敏度和邻位的补偿。假设传感器的零位为a0，被测量的压力值为p，传感器的灵敏度为b0，则可获得传感器室温下电压输出为

U0=a0+b0×p

(1)

无补偿时，传感器在任意温度t环境下的电压输出为

Ut=at+bt×p

(2)

其中

at=a0+α(t-t0)×Y(FS)

(3)

bt=b0+β(t-t0)×Y(FS)

(4)

式中:at为传感器在温度t下的零点;bt为传感器在温度t下的灵敏度；t0为常温温度；α为传感器零点的温度系数；β为传感器的灵敏度温度系数；Y(FS)为传感器的满量程电压输出。

由式(3)、(4)可知,环境温度改变1 ℃，零位温度系数与量程间的比值会出现如下改变：

(5)

式中：Δa为零位的变化值；ΔT为温度的改变量。

环境温度变化1 ℃，灵敏度温度系数和量程间的比值会出现如下改变：

(6)

式中Δb为灵敏度的变化值。

由式(1)～(6)可知，

(7)

将式(7)代入式(1)，得到在t时，经温度补偿后的输出：

(8)

对传感器环境温度进行测量后，可获得有关传感器温度实验的相关数据，当温度上升到一定值时测出的传感器输出为Ut,将Ut值代入式(7)中，最后可计算出温度补偿后传感器的输出值：

当t=0时,有

Ut=at+bt×p=-5.095 9+2.342 6×p

(9)

当t= -20 ℃时，有

Ut=at+bt×p=-6.837 1+2.342 8×p

(10)

当t= -40 ℃时，有

Ut=at+bt×p=-9.245 6+2.534 5×p

(11)

同理可得其他温度点下的输入、输出曲线：

当t= 80 ℃时,有

Ut=at+bt×p=0.876 8+2.022 1×p

(12)

当t= 40 ℃时,有

Ut=at+bt×p=-1.742+2.174 9×p

(13)

由式(9)～(13)可知，灵敏度和零点会随着温度的变化而出现一定的变化，当灵敏度和零点出现变化后，输出的电压也会出现一定的改变。零点温度系数和灵敏度温度系数之间的变化是典型的变化关系，所以，在对零点和灵敏度进行二次拟合的过程中一定要确定温度变化范围的准确性。

2 实验设计

研究过程中所使用到的有关输出和输入的数据如表1所示[6]。假设环境温度为25 ℃时对数据进行线性拟合[7]，最终得到的线形关系式为

Ut=at+bt×p=-2.700 9+2.234×p

(14)

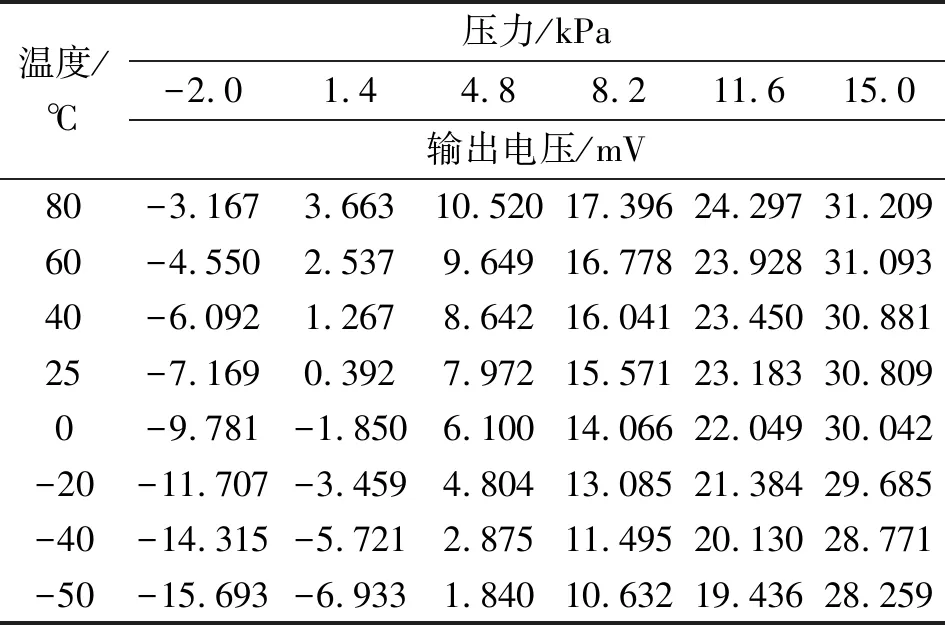
表1 未补偿前全温区性能数据

表2为传感器的零点随温度变化的具体数据。

表2 传感器的零点随温度变化数据

对表2数据进行三阶曲线拟合可得：

at=1×10-0.6t3-0.000 3×t2+0.101 6×t-9.6

(15)

表3为传感器的灵敏度随温度变化的具体数据。

表3 传感器的灵敏度随温度变化数据

对表3数据进行三阶曲线拟合可得:

bt=2×10-0.8x3-7×10-0.6x2-

0.004 5x+2.34

(16)

把零点at和灵敏度bt的拟合曲线代入式(8)可得：

(17)

将环境温度t=-40 ℃,p=-2.0 kPa时、t=80 ℃,p=15 kPa时的数据代入式(17)，两点进行补偿验证。当t=-40 ℃，p=-2.0 kPa时，根据温度实验数据可知，传感器输出电压U=-14.314 5 mV，代入式(17)计算可得Ut=-7.218 9 mV，相对于压力点室温时的电压标定值Uo=-7.169 mV，电压改变量ΔU=0.05 mV；当t=80 ℃，p=15 kPa时，根据温度实验数据可知，输出U=31.209 mV，代入式(17)，最终得到补偿电压U=30.360 6 mV，此时相对应的压力点电压Uo=30.809 mV，ΔU=0.45 mV。

经过算法进行温度补偿后各个温度点的补偿结果如表4所示。传感器温度补偿前、后的曲线如图1、2所示。

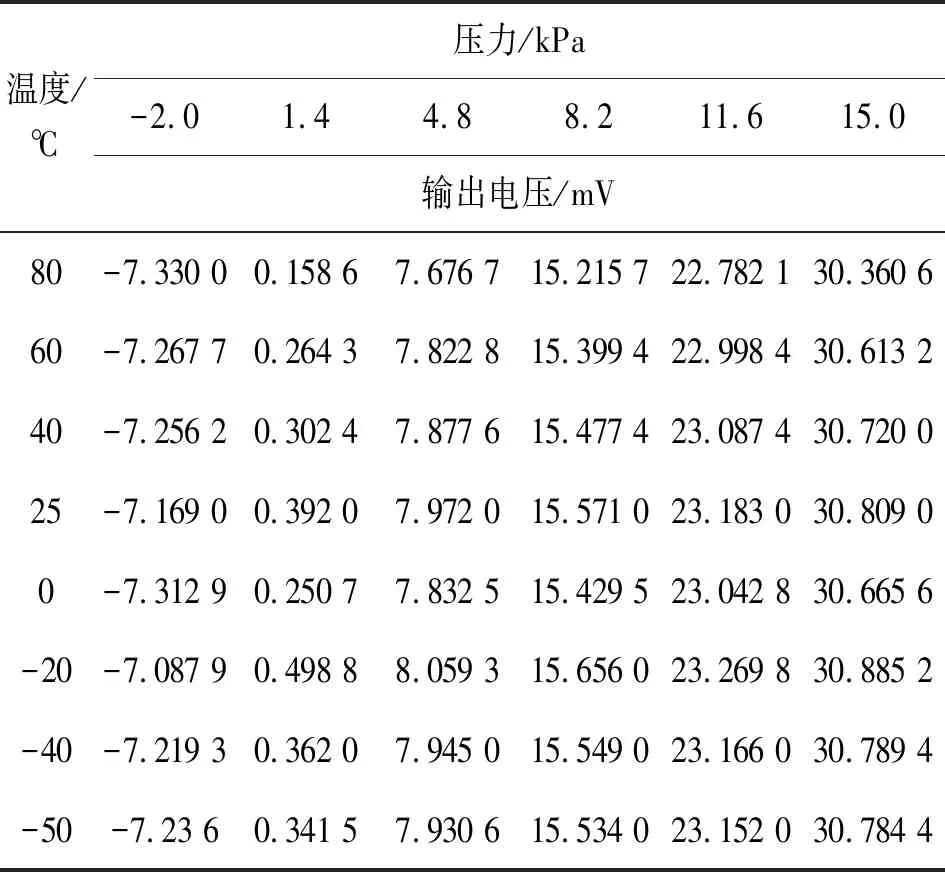
表4 补偿后全温区性能数据

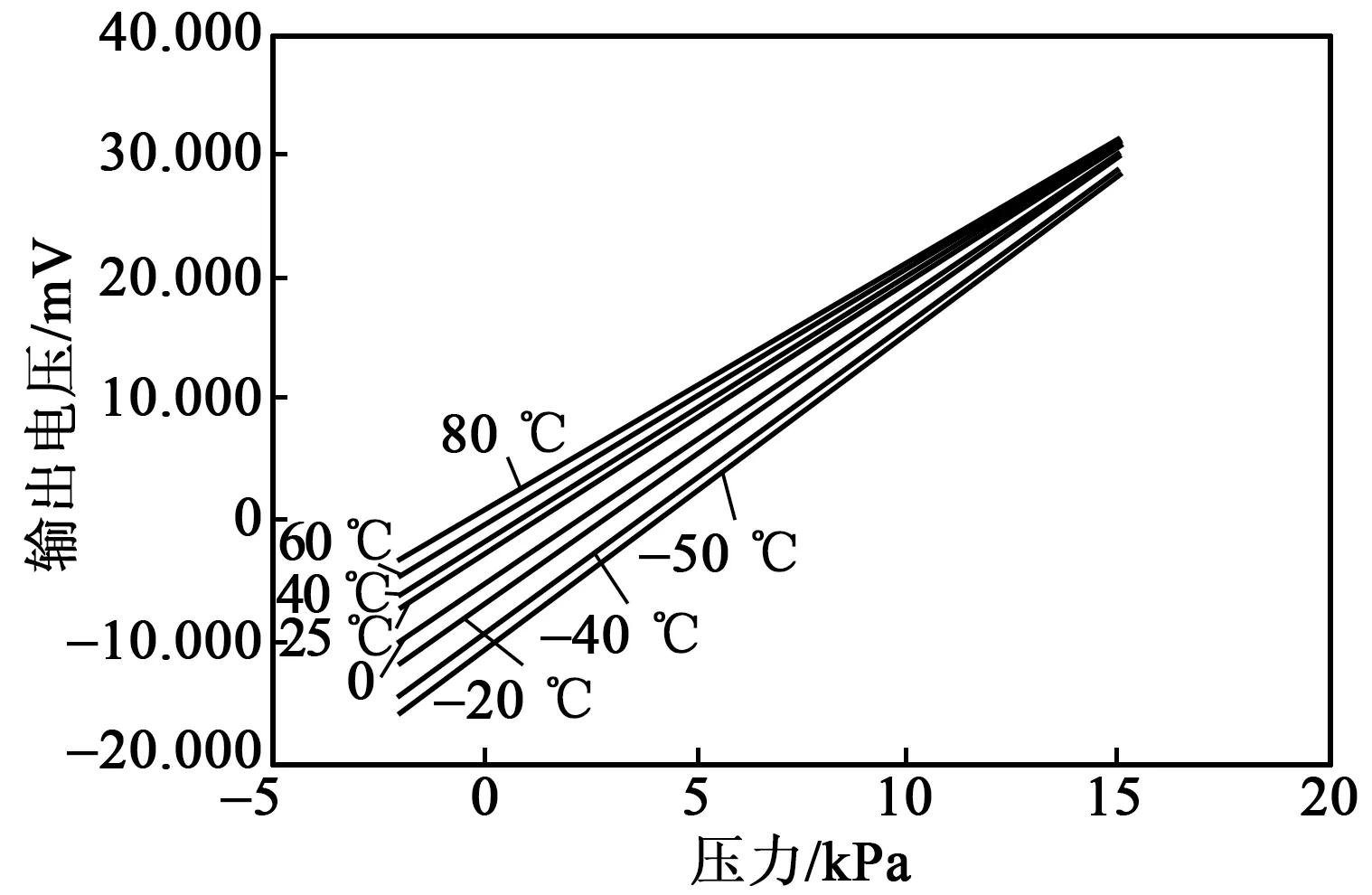
图1 传感器温度补偿前曲线

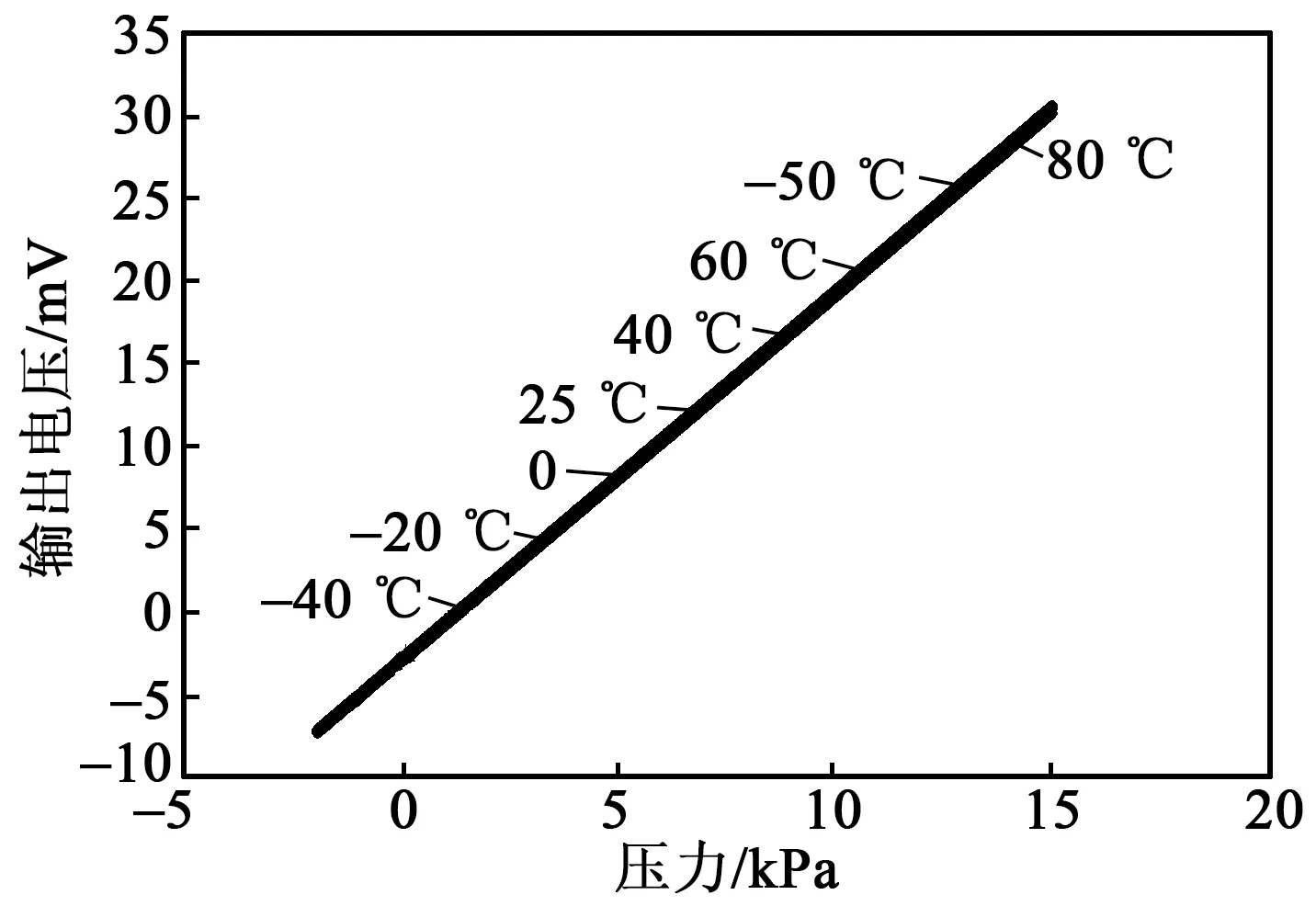
图2 传感器温度补偿后曲线

3 结束语

传感器的灵敏度及零点在温度补偿前出现较明显的变化。经过补偿后，传感器的灵敏度及零点受温度影响降低，精度在温度补偿后上升1个数量级，误差也相应减小，传感器的精确度会在补偿算法后获得进一步提升，且消除了温度这一影响因素对于传感器零点、灵敏度的影响。由于温度补偿的计算量非常小，适合单片机可，广泛应用于工程实践中。