横向电场激励的LiNbO3压电谐振器的仿真分析

鄢 良，马廷锋，王明飞，王 骥，杜建科

(宁波大学 机械工程与力学学院,浙江 宁波 315211)

0 引言

压电晶体谐振器具有高精度、高稳定性和高一致性的特点，在通讯及传感领域中得到广泛应用。传统的压电谐振器通常采用厚度场激励石英晶体谐振器。从激励模式来看，与将电极分别位于谐振器上、下表面的厚度场激励相比，将电极置于同一面上的横向场激励模式具有品质因数高，频率稳定性好及晶体老化率低等优点[1]。之前的横向场激励压电谐振器多采用石英晶体，而石英晶体器件压电耦合系数及传感灵敏度较低，性能亟需提高。因此，有必要研究基于强压电耦合晶体铌酸锂的横向场激励谐振器。

目前，对于横向电场激励谐振器的研究主要还集中在理论上[2-6]，所采用的方法主要是Mindlin一阶板理论，即给定长厚比后，分析简化后的模型振动特性[7]。由于采用一阶板理论得到的解析解只能是一维近似解，得到的结果未考虑宽度方向的影响，而铌酸锂器件由于压电耦合系数高，振动特性受尺寸参数的影响大，因此有必要进行有限元仿真分析，揭示尺寸参数对铌酸锂器件特性的影响规律，为器件的尺寸设计提供参考依据。本文采用有限元仿真分析软件COMSOL Multiphysics，运用三维模型对基于横向电场激励铌酸锂谐振器的高频振动进行仿真分析，得到了厚度剪切振动的导纳图和振型云图。另外,分析了不同结构参数对谐振器谐振频率等振动特性的影响。

1 横向电场激励谐振器的控制方程及频谱关系

图1为横向电场激励谐振器结构图。本文理论计算只考虑振动沿x1方向传播的情况，即x1方向为晶体板长度方向，x2方向为晶体板厚度方向，坐标原点选择为晶体板的中心，谐振器关于坐标原点对称。2h为晶体板厚度，2h′为电极厚度，a，b，c分别表示原点到电极首端、电极尾端及晶体板尾端的距离，其中a值又被称为电极间距值。V，-V表示在两块电极板上分别施加正弦交流电的正、负电压。

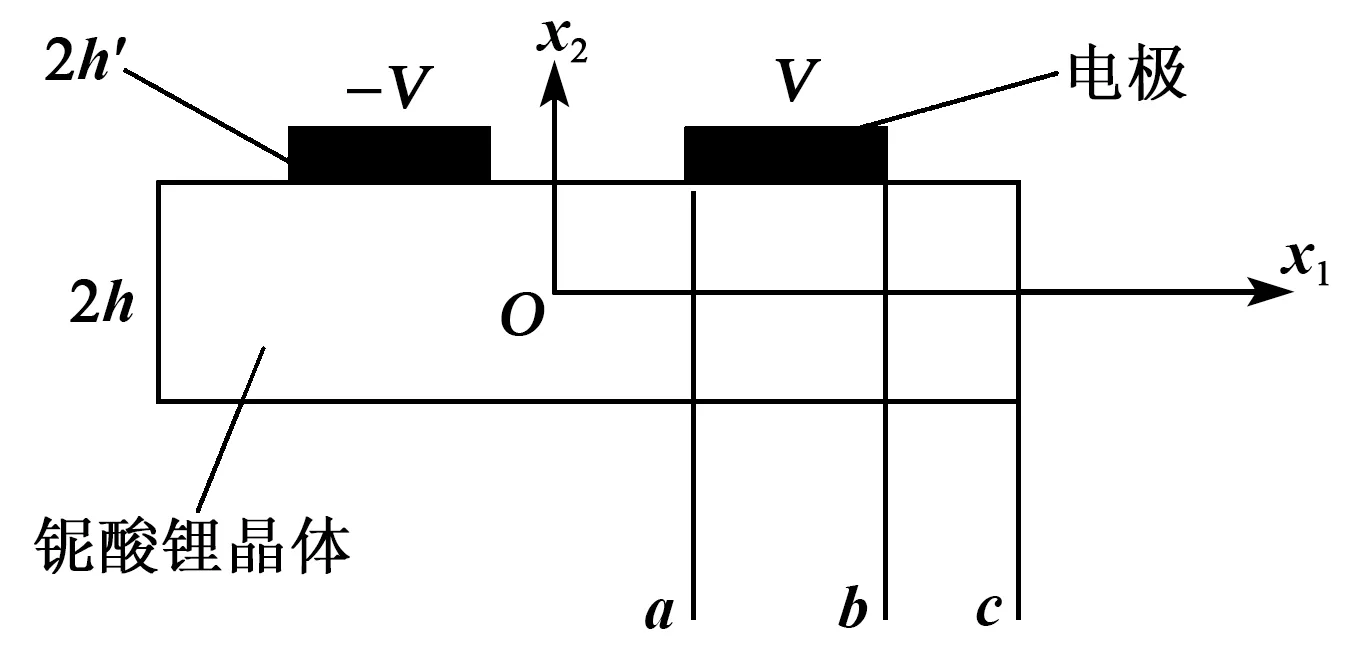
图1 横向场激励谐振器结构图

根据Mindlin一阶板理论，代入相应材料参数，得出一阶板横向场激励谐振器分别在电极区与非电极区的控制方程。

非电极区控制方程：

(1)

电极区控制方程：

(2)

谐振器自由振动边界条件：

(3)

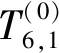
本研究中的工作模态选为厚度剪切模态，振动沿x1方向传播,谐振器材料为(yxl)-58° LiNbO3，电极材料为银,电极与晶体板质量比(r)为0.05，谐振器基频为10 MHz，晶体板宽度为晶体板厚度的60倍。

联立式(1)～(3)，求得谐振器在厚度剪切模态下的频谱关系，如图2所示。

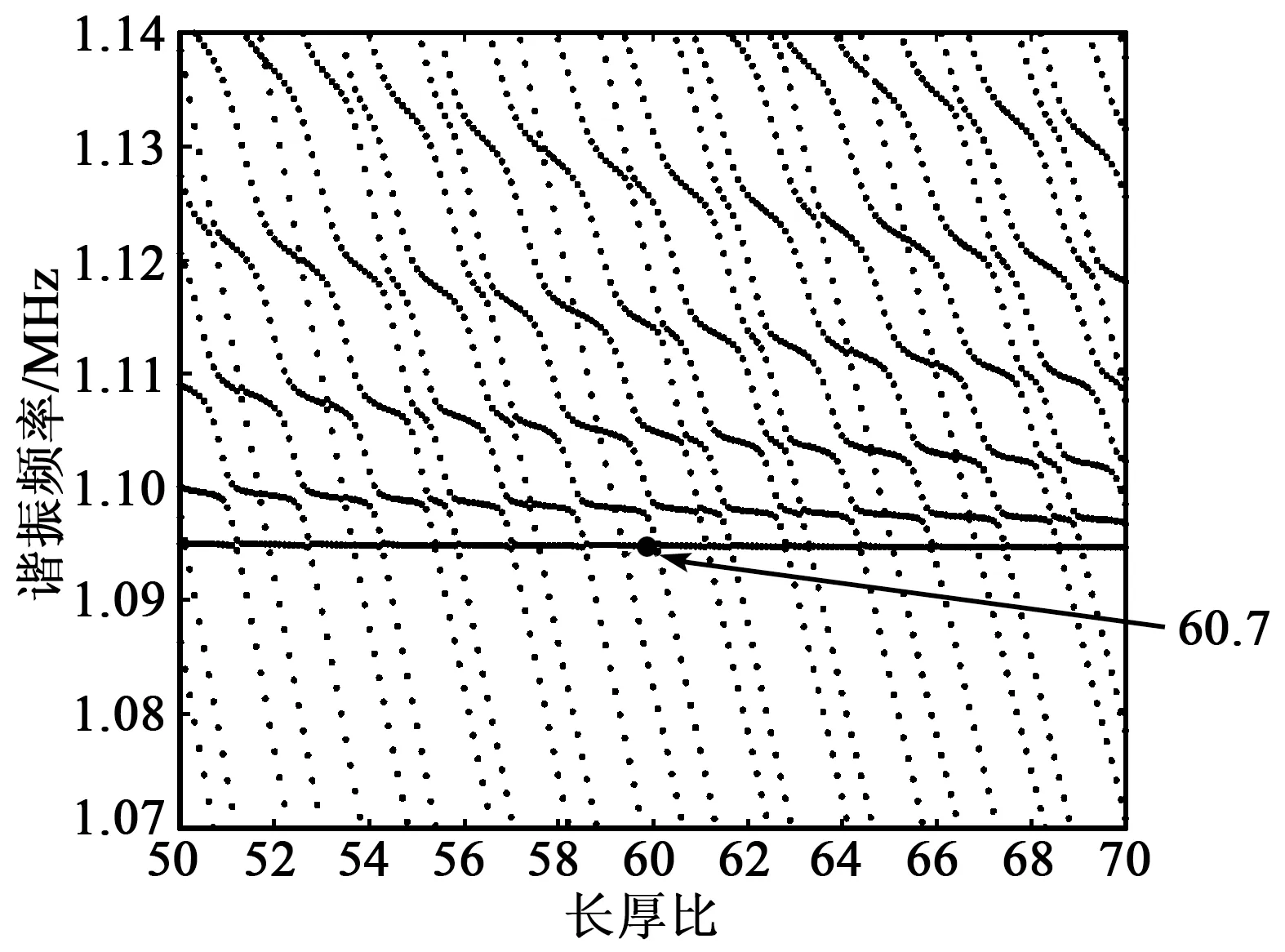
图2 频率与长厚比关系图

为了选择耦合较弱的点，取两曲线的非相交点，本文中选择长厚比为60.7。

根据图2得到的长厚比尺寸，利用有限元分析软件可求解在该尺寸下的厚度剪切模态的谐振频率，进一步分析各个参数对谐振频率和振动强度的影响规律。

2 横向场激励谐振器的仿真

2.1 横向场激励谐振器仿真建模

1)模型结构设计。根据理论计算出的频谱关系选出长厚比，结合给定的宽度及质量比，得到尺寸参数如表1所示。

表1 谐振器尺寸参数表

表1中,w为三维有限元模型中谐振器沿宽度方向的尺寸，其余尺寸参数与二维理论模型代表的含义相同。由表1可知，w与2h′之比大于100倍，在有限元分析中，长厚比相差过大会影响网格划分精度，故对电极做二维化处理，通过在电极区域附加质量的方法补偿由二维化处理带来的误差。

2)模型材料参数设定。COMSOL Multiphysics 中虽然提供了铌酸锂材料参数，但考虑到谐振器有能量耗散，故对材料库中的铌酸锂弹性常数进行修正，其余材料参数保持不变，修正后的铌酸锂弹性常数矩阵为

Cpq=cpq(1+iQ-1)

(4)

式中：p，q=1～6；i表示虚数；Cpq为复弹性常数矩阵；cpq为实弹性常数矩阵；Q=104为耗散因子。

同时在旋转坐标系中，将欧拉坐标系(α,β,γ)设置为(0°,-58°,0°)，得到 (yxl)-58°LiNbO3。

3)模型物理场与边界条件设定。仿真模型物理场选为压电耦合场，在COMSOL Multiphysics中分为固体力学场与静电场。在固体力学场中，模型各边均设为自由边界，模型所有域均设为压电材料域，材料坐标系设为前述的旋转坐标系。同时，需要在固体力学场中设置附加质量，两电极区域质量大小设定为5.914 910-7kg。在静电场中，两电极区域分别设置为终端与接地，终端施加2 V正弦交流电。

4)网格设置。针对矩形板结构，谐振器上表面采用映射网格，然后沿厚度方向进行扫掠。根据理论研究结果，在划分网格时应保证一个波长内至少有8个节点，如此才能保证计算结果的收敛性和正确性[8-9]，因此，网格大小选择为波长的1/8。

2.2 网格无关性分析

模型网格在长度方向的尺寸已确定，为了保证数值计算结果的准确性，将沿厚度方向扫掠的层数分别从1层逐步增加，得到的谐振峰值如表2所示。

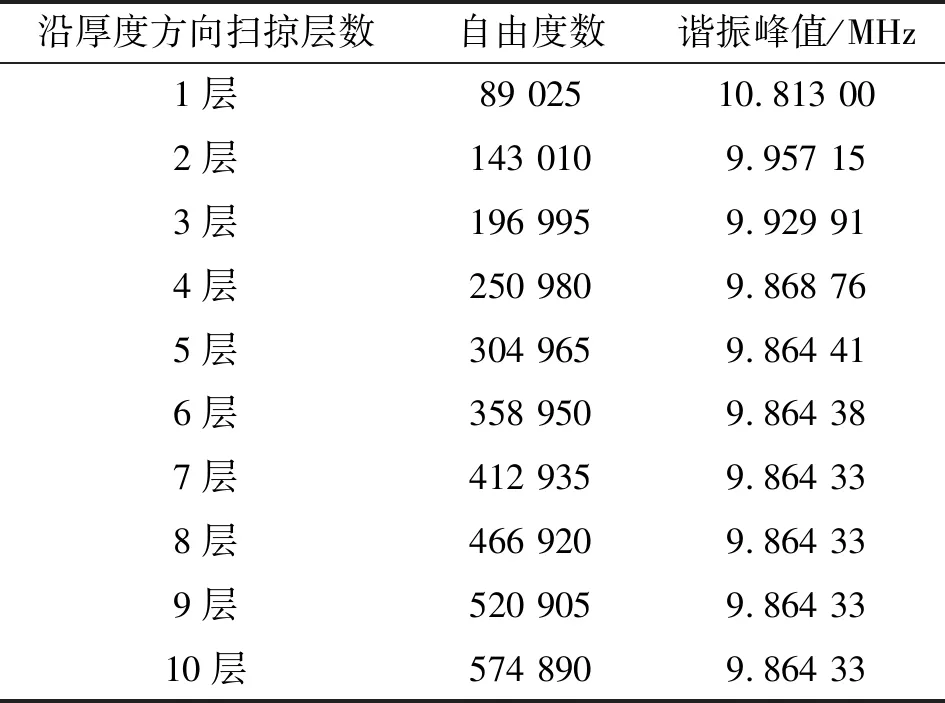
表2 不同自由度下模型谐振峰值

由表2可知，当厚度方向扫掠层数大于7时，谐振器厚度剪切模态的振动频率收敛于9.864 33 MHz。基于表2的结果，同时出于简化计算量的目的，设定沿厚度方向扫掠层数为7层，则谐振器有限元网格模型如图3所示。

图3 谐振器有限元网格模型图

2.3 模态分析

通过求解特征频率的方法找到在10 MHz基频下的谐振器厚度剪切模态，同时，根据计算出的厚度剪切模态对应的特征频率值，在频域计算中进行分析，画出导纳图，得到谐振峰值精确值。谐振器导纳图、谐振峰值点振型云图及谐振峰值点厚度方向位移矢量图分别如图4～6所示。

图4 谐振器导纳图

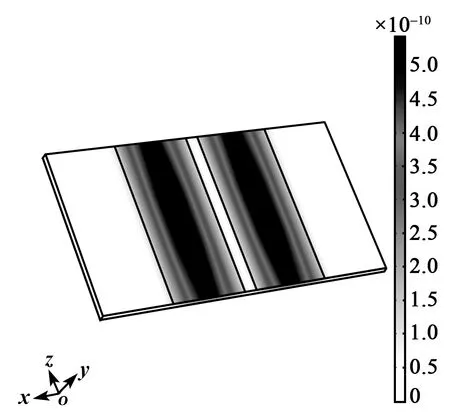
图5 谐振峰值点振型云图

图6 谐振峰值点厚度方向位移矢量图

图4中对应的谐振峰值点为9.864 33 MHz。由图5可知，谐振器振动主要集中在电极区域，且电极区域振动沿宽度方向无变化，非电极区域几乎无振动，谐振器能陷特性好。图6中，振动在厚度方向有一个节点，且位移矢量分布关于节点对称。结合上述分析可确定图4中峰值点所对应的模态为一阶厚度剪切模态。

3 横向场激励谐振器参数优化研究

为了更好地设计性能优良的横向场激励谐振器，通过改变关键结构参数(r，a)及分析各参数对谐振器谐振频率等振动特性的影响。

3.1 r对谐振器影响的研究

在只改变r的条件下，谐振器的谐振频率与总位移曲线分别如图7、8所示。结合图7、8可知，随着r的增加，横向场激励谐振器的谐振频率降低，谐振器电极区的振动强度随之增强，非电极区能陷特性越来越好。电极区振动越强，即谐振器的灵敏度越高。产生该现象是因为随着r的增加，电极导电性增大，谐振器整体阻抗降低，从而使电极区振动强度随之增强，谐振频率随之降低。因此，为了获得灵敏度更高的谐振器，应选择相对大的r。

图7 r与谐振频率关系图

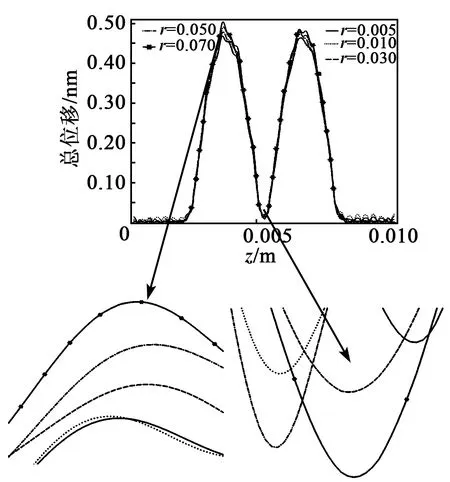
图8 不同r下谐振频率对应的位移曲线图

3.2 a对谐振器的影响

在只改变a的条件下，谐振器的谐振频率与总位移曲线分别如图9、10所示。由图9、10可知，随着a的增大，谐振频率值减小，且频率值减小的速率随着间距值的增大而变慢，谐振器的振动强度先增强后减小，拐点在a=2h附近。产生谐振频率随a增大而减小的现象是因为随着a的增大，谐振器整体阻抗及谐振频率均降低，而振动强度随a的增大呈先增强后减小的现象。这是因为在拐点前后对振动强度产生影响的主导因素不同，在a≤2h时，振动强度大小主要由谐振器整体阻抗决定，随着a的增大，谐振器整体阻抗降低，电极区谐振强度增强；在a>2h时，谐振器振动强度主要由谐振器模态耦合强度决定，随着a的增大，谐振器耦合强度减弱，电极区振动强度减小。因此，应根据谐振器综合要求合理选择a。

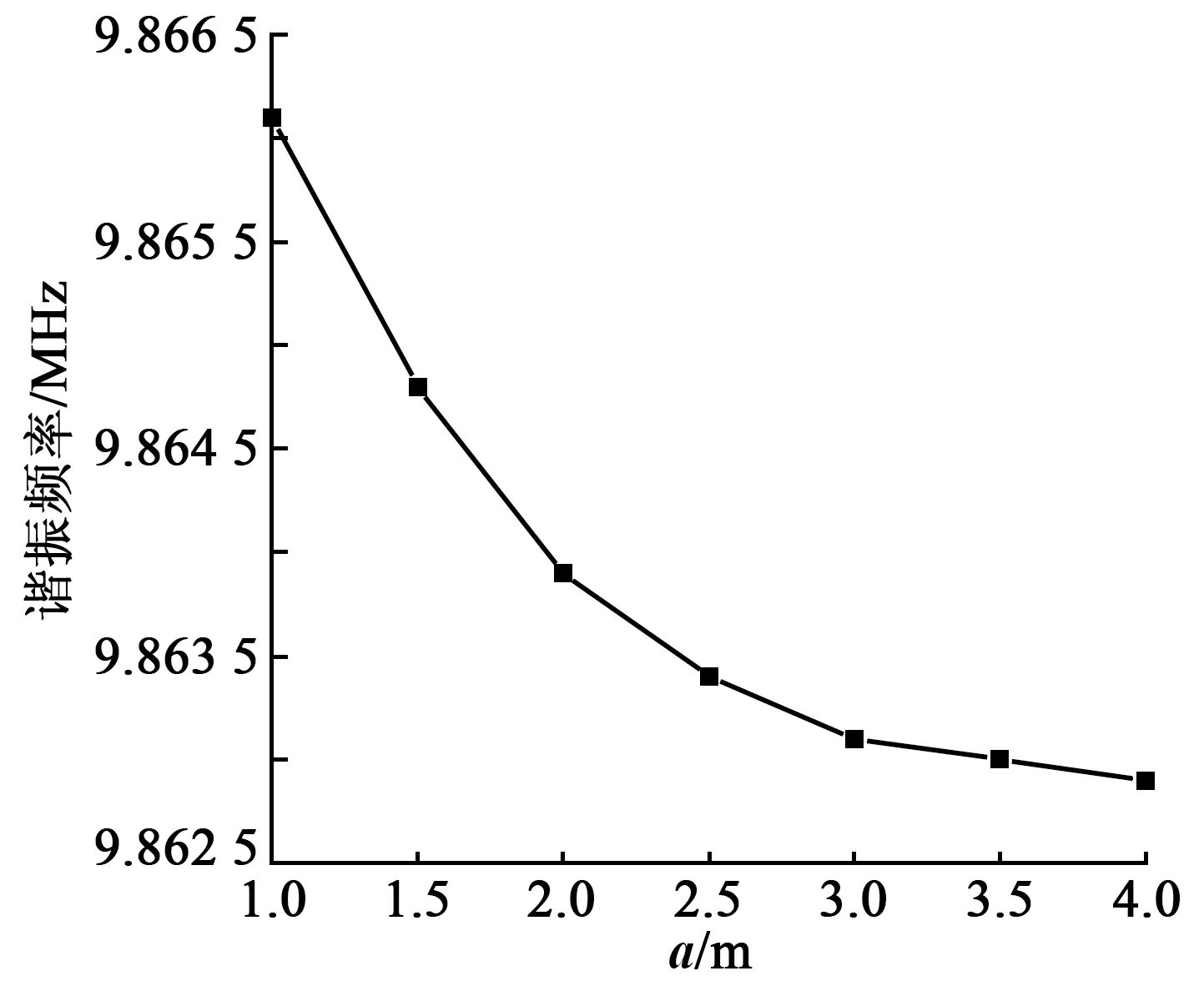
图9 a与谐振频率关系曲线图

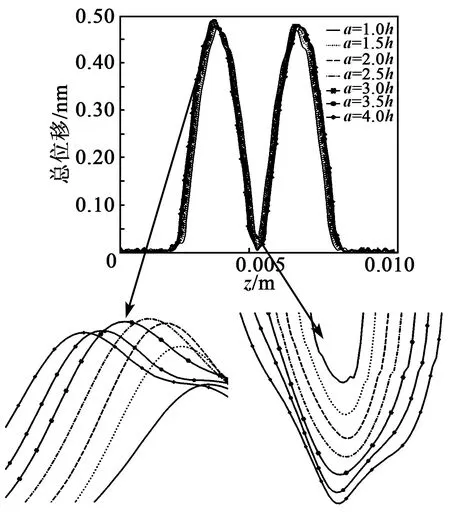
图10 不同a下,谐振频率对应的位移曲线图

4 结束语

本文通过有限元分析软件COMSOL Multiphysics对基于横向电场激励的(yxl)-58°LiNbO3谐振器的高频振动进行了分析，通过Mindlin板方程计算出的频谱关系，结合给定的尺寸参数，得到基频为10 MHz的横向电场谐振器一阶厚度剪切模态频率值为9.864 33 MHz；同时，通过改变关键结构参数，得到了电极质量比与电极间距对谐振器高频振动特性的影响规律：随着质量比的增加，谐振频率降低，能陷效应变好，振动强度增强；随着电极间距的增加，谐振频率降低，能陷效应变好，振动强度先增强后减弱，拐点出现在电极间距值a=2h附近。根据本文的研究结果，在设计横向电场激励的LiTaO3谐振器时，能快速设计出谐振器最优尺寸，对实际生产有重要参考价值。