基于Van der Pol―Duffing振子和互相关的微弱信号检测研究

( 1. 石家庄铁道大学 机械工程学院，河北 石家庄 050043；2. 河北省交通安全与控制重点实验室，河北 石家庄050043 )

0 引言

在现代信息技术处理领域，微弱信号检测一直都是热点和难点，特别是完成对微弱正弦信号幅值及其相位的检测在振动测量、故障诊断生物医学等领域有重要的研究价值。传统的微弱信号检测都是通过信号处理来提高信噪比，最低检测信噪比只有-10 dB[1]。自应用混沌振子对微弱信号进行检测以来，利用混沌振子进行微弱信号检测得到了不断的改进和发展。通过混沌振子对未知信号进行估计，无论是精度上还是信号识别能力上都比以往传统的微弱信号检测方法好。由混沌理论[2-3]可知，混沌振子在一定条件下对微弱信号非常敏感而对噪声具有一定的免疫性[4-5]，当待检信号并入到处于临界状态的混沌系统后会导致系统发生相变[6-8]，由混沌状态变化到周期状态，这一特性使得利用混沌振子检测微弱信号具有独特的优势。近年来，如何进一步降低信噪比门限成为混沌检测的研究热点[9-11]。

自Boxcar积分器出现以后，时域信号处理方法就一直没有重大的改进，而且存在着门限较高，对噪声的抑制能力差等缺点，并且时域信号处理方法所具有的优点如物理意义清晰、无需对噪声分布作假设等没有被完全发挥出来。在时域检测方法中，常用互相关检测方法来检测微弱信号[12]，但是在实际应用中发现，互相关检测方法的积分时间有限，对噪声抑制能力较差，通过此方法得到的信噪比门限比较高。因此，本文提出一种通过Van der Pol―Duffing振子和互相关联合的方法对微弱信号进行检测。此方法既解决了互相关检测方法对噪声抑制不足的问题，又利用了混沌振子对微弱信号的敏感性及对噪声的免疫性。大量的仿真实验结果表明，此方法可极大地降低信噪比工作门限，抗噪性强，是降低信号检测下限的有效方法。

2 基于Van der Pol―Duffing振子检测微弱信号的方法

2.1 Van der Pol―Duffing振子检测弱信号的基本原理

到目前为止，对于混沌振子的研究国内外都比较活跃。其中Van der Pol―Duffing振子是非线性系统中具有代表性的一类系统，它最初是荷兰电子工程师Balthazar Van der Pol为了描述电子电路中三极管的振荡效应而推导出来的，此后众多学者就将Van der Pol―Duffing振子作为一种经典的混沌系统用于动力系统的建模，如今在物理、生物工程、神经学和经济学等领域，很多非线性问题都可以简化成为该系统来进行研究。该系统可随参考信号强度的变化表现出丰富的非线性动力学特性，如倍周期分岔、混沌状态、周期状态等。基于此，本文选择Van der Pol―Duffing振子作为检测微弱信号的混沌系统。不同于常规的基于噪声抑制的检测方法，混沌振子是通过直接提取信号从而完成对微弱信号的检测[13-19]。由于混沌系统对噪声具有很强的免疫力，而对微弱信号非常敏感，通过Simulink可对Van der Pol―Duffing系统进行建模并仿真，只输入纯噪声时的相图为混沌态，当输入微弱信号时相图会由混沌态跃迁到周期态，此时说明已检测到微弱信号且信噪比门限很低，因此，混沌系统检测微弱信号非常具有优势。

2.2 数学模型及仿真模型的建立

Van der Pol―Duffing振子的一般形式如下

(1)

式中，u和α是2个正系数；F和ω分别是参考信号的幅值和频率。

式(1)的状态方程为

(2)

由于此混沌振子对初始值敏感及对噪声具有强免疫力，因此可以通过混沌态和大尺度周期状态间的相轨迹改变来检测微弱信号。对于式(2)所描述的混沌系统，当系统处于混沌态和周期态的临界状态时，向其输入含有噪声的待检正弦信号(与参考信号同频率，同相位)，有

(3)

式中,Fs是混沌系统的临界阈值;F1cos(ω1t)是待检信号;n(t)为高斯白噪声，n(t)=σ·ε(t)。通过Simulink建立仿真模型，采用定步长四阶龙格—库塔法，取步长h=0.01 s。

2.3 仿真结果

仿真时，Fs取值5.03，ω取值2.463 rad/s，u=5，α=0.01，系统初始值为(0.1,0.1)。当只有噪声加入混沌系统时，系统的相轨迹没有发生变化，处于混沌状态，如图1。此时的σ取值为0.05。

在之前仿真的基础上，当把噪声和待检信号(与参考信号的频率一致)并入系统后，此系统的相轨迹由原来的混沌态跃迁到稳定的周期态，如图2所示。

此时的待检信号的幅值是未知的。因为|F1+Fs|>Fs，因此，当把待检信号并入到混沌系统后，系统的相轨迹发生改变，由混沌态变为周期态。通过减小Fs，可使得系统再次回到临界状态，得到新的参考信号幅值Fs1。那么待检信号的幅值可由参考信号幅值的改变量来确定，即F1=Fs-Fs1。而当只把噪声加入系统时，由于混沌系统对噪声具有强免疫力，不会引起相变。由上述理论可知，本文进行仿真时的待检信号幅值为0.01。

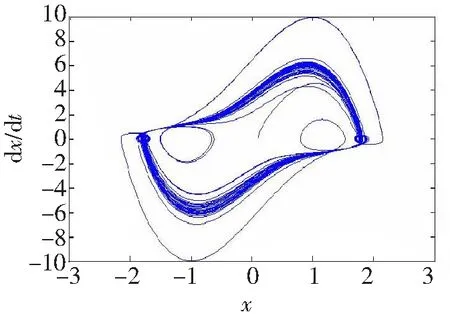
图1 σ =0.05时，系统处于混沌态

图2 系统处于周期状态

3 利用互相关检测微弱信号的原理

互相关方法在信息科学领域应用非常广泛，由于信号在相关特性上和噪声具有不同的特点，通过将待检信号(含有噪声)和参考信号(纯正弦信号)进行互相关运算，可实现对噪声的抑制和对正弦信号的有效提取。以下为互相关法检测微弱信号原理。

待检信号

f1(t)=s1(t)+n(t)

(4)

参考信号

f2(t)=s2(t)

(5)

式中，s1(t)和s2(t)为周期信号；n(t)为噪声。则互相关函数如下

(6)

式中，Rs1s2(τ)是s1(t)和s2(t)的互相关函数；Rns2(τ)是n(t)和S2(t)的互相关函数。在式(6)中，参考信号s2(t)与噪声信号n(t)不相关，若s2(t)与n(t)或s2(t)的均值为0，则其互相关函数为0。因此，只需s1(t)与参考信号s2(t)互相关，则Rns2(τ)=0,R12(τ)=Rs1s2(τ),这说明根据互相关函数R12(τ)的运算结果就可以检测到淹没在噪声中的微弱正弦信号。理论上，积分时间T够长，Rns2(τ)就为0，但是实际上T不可能无限长，只能为某一有限值，因此，Rns2(τ)不等于0，而是接近于0的随机变量，所以输出仍存在残余噪声。

图3是淹没在高斯白噪声中的待检信号的时域波形图。图4是对混有噪声的待检信号与参考信号做互相关运算得到的函数曲线。

图3 待检信号的时域波形

图4 互相关函数R12(τ)

由图4看出，由于积分时间不可能无限长，互相关检测法不可能完全过滤掉噪声，这给检测所包含的微弱信号带来一定难度。对包含微弱信号的噪声进行一次互相关后，噪声虽然得到一定程度的抑制，但是并不能无限制地多次使用：一是每进行一次互相关处理后数据的长度都会减少，如果减少太多，不利于检测效果；二是多次互相关以后波形会出现平顶失真的现象，这是由多次计算后产生的截尾误差引起的，因此不可能无限制地使用互相关来进行微弱信号检测。其次，互相关处理后不可避免地会存在边缘效应问题，即信号边界产生失真现象，进行多次互相关后产生的边缘效应会放大，严重淹没信号的端部特征，极大影响检测效果的准确性。最后，互相关检测方法不能对信噪比很低的微弱信号进行检测。为解决上述问题，可应用混沌理论来检测微弱信号。

4 基于Van der Pol―Duffing振子和互相关的微弱信号检测

为了能进一步降低信噪比工作门限，提高微弱信号检测的效果，同时解决互相关检测方法本身的不足，把Van der Pol―Duffing振子与互相关方法联合起来对微弱信号进行检测。关于微弱正弦信号检测的具体步骤如下。

首先找到混沌系统处于临界状态时参考信号的幅值Fs，然后把噪声和待检信号一起输送到互相关器中，求得输入信号和参考信号的互相关函数。由前面理论分析可知，在此过程中已经对噪声进行了一定的抑制，但仍保留有残余噪声。最后，将得到的互相关函数并入到Van der Pol―Duffing系统当中，由于此系统对于本身参考信号频率相同的周期信号非常敏感而对噪声具有强免疫性，因此，混沌系统会进入到周期状态，根据相图的变化即可判断输入信号中是否含有微弱正弦信号。该方法的原理如图5。

图5 Van der Pol―Duffing振子与互相关方法联合检测原理图

根据上述理论，选取σ=0.09，待检信号的幅值F1取0.01来进行检测。单Van der Pol―Duffing振子的检测效果如图6所示，Van der Pol―Duffing振子与互相关联合检测的效果如图7所示。由图6和图7的对比可知，在一定条件下单Van der Pol―Duffing振子检测不到微弱信号，而基于Van der Pol―Duffing振子和互相关的方法可以很好地完成对微弱信号的检测。仿真实例说明本文方法比单Van der Pol―Duffing振子检测微弱信号更具有优势。

图6 单Van der Pol―Duffing振子的相轨迹

图7 Van der Pol―Duffing振子与互相关联合系统的相轨迹

可见，本文方法可以降低强噪声条件下微弱信号检测的信噪比门限。

5 与单Van der Pol―Duffing振子性能比较

本节的目的是比较两系统的稳定性和抗噪性能，不是对微弱信号进行检测，因此未将微弱信号单独写出。对于微弱信号检测，当系统由临界状态进入到大尺度周期状态，此状态的稳定性对于系统的判别非常重要，这里分别利用单Van der Pol―Duffing振子和Van der Pol―Duffing振子与互相关联合系统在不同强度噪声背景中的稳定性进行分析。当参考信号的幅值Fs取值为5.05时，两系统都处于周期状态。当向两系统输入σ分别为0.5和1的纯噪声后，两个系统在不同强度噪声中的运动相态如图8和图9。由图8和图9可见，在不同强度噪声下，虽然Van der Pol―Duffing振子与互相关联合系统的运行轨迹较为粗糙，但仍处于周期状态，而单Van der Pol―Duffing振子则处于混沌态。通过两图的对比可以发现，Van der Pol―Duffing振子与互相关联合后抗噪性更强。

图8 σ=0.5时两系统的相态图

图9 σ=1时两系统的相态图

6 结论

首先分别介绍了利用Van der Pol―Duffing振子与互相关检测微弱信号的基本方法，然后在此基础上，提出了二者联合的微弱正弦信号检测方法。通过对联合系统进行仿真，其可以检测到深埋于噪声中的微弱信号，信噪比工作门限也进一步下降，达到了-43 dB，而利用单Van der Pol―Duffing振子只有-20 dB。通过输入不同程度的纯噪声和单Van der Pol―Duffing振子进行对比，联合系统仍能保持周期态，而单Van der Pol―Duffing振子已处于混沌态，说明联合系统对强噪声具有更好的免疫力，证明了该方法的有效性。