例说待定系数法的应用

2019-06-25筅山东省济南市莱芜雪野镇中心中学王春香

中学数学杂志 2019年10期

筅山东省济南市莱芜雪野镇中心中学王春香

初中阶段我们所学的函数有三种：一次函数（一般形式为y=kx+b，其中k≠0）、反比例函数（一般形式为y=，其中k≠0）和二次函数（一般形式为y=ax2+bx+c，其中a≠0）.在解决这些与函数有关的问题时，经常需要求出函数的解析式.例如，已知抛物线y=ax2+bx+c经过A、B（1，6）、C（2，4）三点，求二次函数y=ax2+bx+c的最大值.解答此题需要先设二次函数的解析式为y=ax2+bx+c，然后将A、B（1，6）、C（2，4）三点的坐标代入二次函数的解析式，得到一个三元一次方程组，最后解这个三元一次方程组求出a、b、c的值，这样便可求出二次函数的解析式，从而求出二次函数的最大值.我们把这种解决数学问题的方法叫作待定系数法.在解决数学问题时，有时我们可以先根据题意设出某一含有待定系数的等式，然后利用已知条件列出关于待定系数的方程（组），最后通过解方程（组）求出待定系数，从而顺利表示出所设等式，进而利用该等式解决问题，这种解决数学问题的方法就叫待定系数法.待定系数法是中学数学中一种常用的方法，下面以例子分类说明待定系数法在解决初中数学问题中的应用.

一、利用待定系数法求三角形的面积

例1如图1，一次函数的图像经过A（2，3）、B（0，1）两点，与x轴交于点C，求△AOC的面积.

分析：要求△AOC的面积，由于OC边在x轴上，我们可以以OC为底边，则点A的纵坐标3即为该边上的高，下面只需求出OC边之长.可先利用待定系数法求出直线AB的解析式，进而求出点C的横坐标.

解：设直线AB的解析式为y=kx+b.

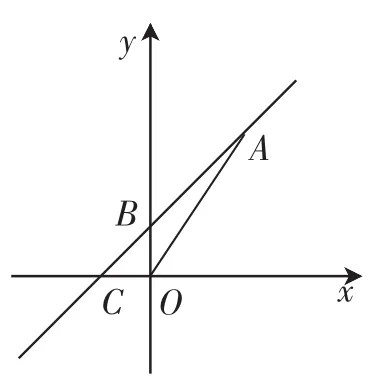
图1

则直线AB的解析式为y=x+1.

令y=0，得x=-1.则点C（-1，0）.

S△AOC=

说明：在求平面直角坐标系内某一三角形的面积时，尽量选取三角形在坐标轴上的某边作为底边，如上述解法中△AOC的边OC在x轴上，因此我们选取OC边为底边.当然本题也可选取OB边作为底边，则S△AOC=S△AOB+S△COB=另外，本题除了利用待定系数法求解，还可以利用相似的知识求解.如图2，过点A作AE⊥y轴于点E，易证△ABE△CBO.则而BE=OEOB=3-1=2，则则OC=1.这样也可以求出OC.因此我们要具体问题具体分析，灵活根据题目特点解题，切忌生搬硬套.

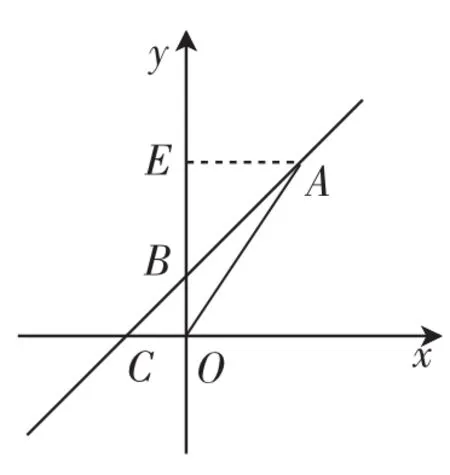
图2

二、利用待定系数法求代数式的值

例2 王阿姨和李阿姨到同一水果超市购买水果.王阿姨购买5斤红富士苹果、13斤赣南脐橙、1斤广西龙眼，共花了111元；李阿姨购买4斤红富士苹果、10斤赣南脐橙、1斤广西龙眼，共花了88元.根据上述信息，你能算出购买1斤红富士苹果、1斤赣南脐橙、1斤广西龙眼一共要花多少钱吗？

分析：设1斤红富士苹果的价格为x元，1斤赣南脐橙的价格为y元，1斤广西龙眼的价格为z元.根据题意可得方程组有两个方程但有三个未知数，无法求出未知数的值.但根据题意可知，要求购买1斤红富士苹果、1斤赣南脐橙、1斤广西龙眼一共要花多少钱，实际上就是求x+y+z的值.我们的解题目标是求x+y+z的值，而不是求出每个未知数的具体值，那么应该怎么办呢？我们应该设法用含有5x+13y+z和4x+10y+z的式子表示出x+y+z，再求x+y+z就方便多了，这可借助待定系数法.

解：设1斤红富士苹果的价格为x元，1斤赣南脐橙的价格为y元，1斤广西龙眼的价格为z元.根据题意，可得5x+13y+z=111，4x+10y+z=88.

设x+y+z=m（5x+13y+z）+n（4x+10y+z）.

即x+y+z=（5m+4n）x+（13m+10n）y+（m+n）z.

利用对应项的系数相等，得5m+4n=1 ①，13m+10n=1 ②，m+n=1 ③.联立①和②，得得代入③，也成立.

则x+y+z=-3（5x+13y+z）+4（4x+10y+z）=-3×111+4×88=19.

所以购买1斤红富士苹果、1斤赣南脐橙、1斤广西龙眼一共要花19元.

说明：上述解法是利用待定系数法求解，我们也可以视某一未知数为常数，将原方程组转化为二元一次方程组求解，如视z为常数，将原方程组转化为解得则x+y+z=（17-1.5z）+（2+0.5z）+z=19.还可以利用分离系数法，将x+y+z从两个方程中分离出来，将方程组变形为（视x+y+z和2y-z为整体），或（视x+y+z和2x+3z为整体），（视x+y+z和x+3y为整体）的形式，这样也可通过解二元一次方程组求解.

三、利用待定系数法分解因式

例3分解因式3x2+5xy-2y2-5x+11y-12.

分析：这是一个二次六项式.由于项数较多，无疑增加了分解难度.我们可以对原式进行分组，然后运用待定系数法求解.

解：按二次项、一次项、常数项对原式进行分组，得原式=（3x2+5xy-2y2）+（-5x+11y）-12.

3x2+5xy-2y2=（3x-y）（x+2y）.

设原式=（3x-y+m）（x+2y+n），展开整理，得3x2+5xy-2y2+（m+3n）x+（2m-n）y+mn.

利用对应项的系数，得m+3n=-5 ①，2m-n=11 ②，mn=-12 ③.

则原式=（3x-y+4）（x+2y-3）.

说明：上述解法是按次数分组，也可将原式整理为关于某一字母的二次三项式，然后分组，如将原式整理为关于x的二次三项式，得3x2+（5y-5）x-2y2+11y-12，先对-2y2+11y-12因式分解，得-2y2+11y-12=（-y+4）（2y-3）. 设原式=（mx-y+4）（nx+2y-3），展开整理，得mnx2+（2m-n）xy+（-3m+4n）x+11y-12.利用对应项的系数相等，得mn=3 ①，2m-n=5 ②，-3m+4n=-5 ③.联立②和③，得解得代入③式，也适合.则原式=（3x-y+4）（x+2y-3）.