“链条式”课堂，别样精彩*——一节全国展示课“同底数幂的乘法”引发的思考

筅江苏省南京市致远初级中学 何君青

随着《普通高中数学课程标准（2017年版）》的出台，初中新一轮课程标准的修订也全面开展，这为教师课堂教学的有效实施增添了无限的思考.不久前，笔者在《中学数学》等杂志发表了多篇文章，讲述对课堂教学的新思考——“链条式”课堂教学，这种教学模式是对“三个理解”“学科核心素养”“学科关键能力”很好的诠释.它从学生的已有知识出发，以一个又一个问题展开，通过“链条”般的系列问题让学生达到对知识的透彻掌握.近期笔者受邀去山西上了一节展示课，就用了此模式授课，现撰文与同行交流.在授课前后，为了能更好地掌握学情，走向基于证据的教学，笔者还融入了一些信息化手段.

一、教学分析

“同底数幂的乘法”选自北师大版教材七年级下册第一章第一节内容.同底数幂的乘法运算是幂的运算中重要的一种运算，它是在有理数的乘方和整式的加减基础上发展起来的，它使同底数幂的乘法的结果更为简洁、方便.同底数幂的乘法是学习整式的乘、除运算的基础，是幂的三个性质中最基本的一个性质，可见同底数幂的乘法运算的学习架起了“有理数的乘方”与“幂的运算”、“幂的运算”与“整式的乘、除运算”之间联系的桥梁，起到了承上启下的作用.本节课的授课内容属于规则下的概念教学课，在教学时，需要逐步让学生理解相应概念，不要操之过急，尽量在经历同底数幂的乘法运算性质的探索过程中，体会同底数幂的乘法运算的实际意义，感受法则的合理性，发展应用数学知识的意识与能力.

基于此，笔者制定了本节课的教学目标.

（1）了解同底数幂的乘法的运算性质，理解符号表示同底数幂的乘法运算性质的意义，体会模型思想，发展符号意识.

（2）会正确运用同底数幂的乘法运算性质进行运算，并知道每一步运算的依据.

（3）经历探索同底数幂乘法运算性质的过程，感受从特殊到一般、从具体到抽象思考问题的方法，发展数感和归纳的能力，积累探究数学公式的活动经验.

在学习本节课时，学生已经有了一定的基础，已掌握了有理数的相关运算，并已初步具有用字母表示数的思想，但用字母来归纳同底数幂的乘法法则，使其具有一般性，对学生的抽象思维能力和逻辑推理能力要求较高.所以本节课主要的任务就是让学生理解同底数幂的乘法运算性质，能熟练地进行同底数幂的乘法运算，并能用同底数幂的乘法解决简单的实际问题.在教学过程中，学生需要经历同底数幂的乘法运算性质的探索过程，体会同底数幂的乘法的实际意义，感受法则的合理性，并通过观察、归纳、发现、概括等过程发展应用数学知识的意识与能力.

基于此，制定了本节课的教学重点和难点.

重点：

（1）能借助文字语言和符号语言表述同底数幂的乘法运算性质.

（2）会正确地运用同底数幂的乘法运算性质进行运算，并知道每一步运算的依据.

难点：

在推导同底数幂的乘法运算性质的过程中，渗透化归思想，并培养学生的归纳能力.

在同底数幂乘法法则得出时，很多教师有这样两种操作方案：通过1至2个生活情境中的例子，让学生进行具体数字底数的同底数幂的乘法，于是归纳出同底数幂乘法的法则；通过2至3个算式，让学生说说发现，从而归纳出同底数幂乘法的法则.这两种做法类似，都是通过几个例子的计算，发现共同的特征，从而抽象出概念，归纳出同底数幂乘法的法则.很多教师上课时都是采用这两种方式，这样的做法仅仅是记忆认识，并没有过多知识形成的过程，学生其实并不能真正理解算理，也不会真正掌握日后研究类似问题的一般方法.

在本节课巩固练习时，大部分教师会通过大量的练习，让学生进行操练，从而掌握同底数幂乘法的法则解决相关问题，稍微好一点的教师会做一些逆向思维的问题，加深学生对同底数幂乘法法则的认识.此类做法过于机械，让学生成为学习的工具，学习数学的兴趣日后会大打折扣，更不会形成探索问题的一般方法和有效策略.

基于上述考虑，笔者在设计本节课时，打算独辟蹊径，从数学问题（有理数的乘方）入手，让学生一开始“摸得到，看得着”，接着提出“108×107如何计算”，将熟悉问题转换成陌生问题，初步感受到同底数幂是可以相乘的，继而让学生尝试计算两组算式，并寻找算式中蕴含的规律，再将规律用数学式子表示出来，让学生再次感受同底数幂的乘法运算，接着通过一系列的练习加深学生对同底数幂的乘法运算性质的理解，最后通过对多个同底数幂的相乘的研究，深刻领悟同底数幂的乘法运算的内涵.研究过程由浅入深，通过从特殊到一般再到更一般、从具体到抽象的过程，配合相应例题、练习题的训练，体会同底数幂的乘法运算性质，最终将两个同底数幂相乘的法则推广到多个同底数幂相乘的法则，达到经验的迁移、能力的提升.在课堂中使用信息化手段检测学生当堂掌握的情况，及时批改和实时的作业报告第一时间反馈整个班级的情况，当堂解决学生问题.

二、教学过程

1.前测准备，了解学情

通过使用信息化手段，上课前一天给学生布置前测作业，了解学生对幂的意义、单项式指数等定义的掌握情况，从学生解答的情况，估计学生第二天学习本节课内容时可能出现的状况，从而调整第二天上课的内容.

具体题目如下.

（1）x3表示（ ）.

A.3x B.x+x+x C.x·x·x D.x+3

（2）关于（-7）2，下列说法正确的是（ ）.

A.-7是底数，2是幂 B.7是底数，2是幂

C.7是底数，2是指数 D.-7是底数，2是指数

（3）关于-43，下列说法正确的是（ ）.

A.-4是底数，3是幂 B.4是底数，3是幂

C.4是底数，3是指数 D.-4是底数，3是指数

（4）计算a3·a4的结果是（）.

A.a4B.a6C.a7D.a12

（5）若am=3，an=2，则am+n的值是（ ）.

A.5 B.6 C.8 D.9

2.教学情境，引入新课

在学习乘方运算时，曾学过an，还记得an表示什么意义吗？当时a称为什么？n称为什么？an这个整体呢？

你能解释108的意义吗？107又是何意义呢？

若今天将108与107相乘，你能算出它们相乘的结果吗？如何解释？

设计意图：从已知问题入手，让学生感觉熟悉，通过一再的追问，使学生感受到知识难度不断上升的过程，为后面将未知问题转换成已知问题、将陌生问题转换成熟悉问题提供背景.

3.探索活动，明晰本质

［活动一］

对于两个底数不是10的幂相乘，刚才的方法继续适用吗？不妨试试看！

25×28=______；

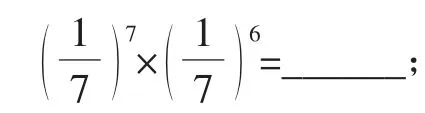
（-3）6×（-3）3=______.

你还能举出几个类似的例子，并计算它们的结果吗？

［活动二］

将这些幂的形式变得更一般，若这些幂的指数换成字母，又会得到怎样的结果呢？

2m×2n=______；；

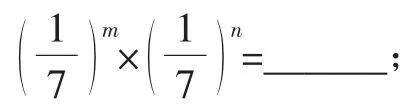
（-3）m×（-3）n=______.（其中m、n都是正整数）

观察上述这些式子，你有什么发现呢？你能用符号表示这个发现吗？对于这个结论，你能解释其中的道理吗？你能用文字表述这个结论吗？

设计意图：让学生先自己尝试计算同底数幂的乘法算式，再观察一系列算式的异同，通过比较、观察，根据从特殊到一般的规律归纳出同底数幂的乘法运算的法则.

再来看一下学生归纳出的结论：am·an=am+n（m、n都是正整数）.

同底数幂相乘，底数不变，指数相加.

4.尝试解决，巩固新知

例1计算：

（1）（-3）7×（-3）6；

（3）-x7·x4；

（4）b2m·b2m+1.

设计意图：4个题目各具特点，第（1）题与第（2）题是底数和指数均为数的同底数幂的乘法，较为简单；第（3）题是底数是字母、指数是数字的同底数幂的乘法，但由于前面多一个负号干扰，难度增大；第（4）题是底数、指数均为字母的同底数幂的乘法，难度较大.4道题都是强化学生对同底数幂的乘法的认识，此环节建议教师板书，运算过程尽可能写得详细.

例2一颗卫星绕地球运行的速度是8×103m/s，这颗卫星运行3×102s的路程是多少？

设计意图：此题是一个实际问题，让学生体会生活中处处有数学的观念，培养学生解决问题的能力和数学应用的意识.在解决此问题的同时，回顾了用科学记数法表示较大的正数，为后续学习用科学记数法表示较小的正数奠定了基础.

［练习一］（信息化平台展示）

（1）计算34×35的结果是（ ）.

A.3 B.35C.39D.320

（2）计算a4·a2的结果是（ ）.

A.a2B.a4C.a6D.a8

（3）计算-x2·x3的结果是（ ）.

A.x5B.-x5C.x6D.-x6

（4）若x3·xm=x6，那么m的值是（）.

A.2 B.3 C.4 D.5

（5）下列计算正确的是（ ）.

A.a3·a2=a6B.b4·b4=2b4

C.x5+x5=x10D.y7·y=y8

（6）下列各式中，填入“-a”后成立的是（ ）.

A.-a3·（）4=a12B.（-a）7·（）5=a12

C.-a6·（ ）6=a12D.a13+（ ）=a12

（7）计算：52×57=______；x3·x9=______.

（8）填空：a4·______=a11；an+2·______=a2n+2.

（9）计算：a·a5+a3·a3=______.

（10）一种电子计算机每秒可做4×109次运算，那么它工作5×102s可做______次运算.

设计意图：本环节进一步强化学生对同底数幂的乘法的认识.此练习借助“悠数学”的及时评价方式，更为迅速地发现学生存在的问题，并及时解决.

［练习二］

计算：

（1）（-7）2×78；

（2）（m+n）3·（m+n）4；

（3）a·am·am+1.

在解决这几道题的过程中，你有什么发现呢？

设计意图：加深学生对同底数幂的乘法的认识.本环节是同底数幂的乘法运算的延伸.3道题的设置各有目的：第（1）题让学生了解到有时候计算时底数不同，不能用同底数幂的乘法法则，要想办法转化；第（2）题让学生了解到同底数幂的乘法法则当底数为多项式时仍然适用；第（3）题让学生了解到计算时有时会出现多个同底数幂相乘的情况，要想办法得到更为一般的结论.

［拓展］

（1）若3×27×9=3x，求x的值；

（2）已知4m=a，4n=b，求4m+n+1.

设计意图：本题组有一定的难度，从思想、方法层面进行拓展，考查学生的逆向思维，渗透化归思想.

5.小结思考，提炼总结

通过今天的学习和研究，你对同底数幂的乘法运算有了哪些认识？

回到最初的地方，一开始我们研究了108×107，若将“×”变成“÷”、“+”或“-”，又会出现什么新问题呢？带着疑问，回家思考一下，你对今天知识的体会会更深！

设计意图：学习本节课的基本目的是了解同底数幂的乘法运算的法则，并运用法则进行同底数幂的乘法运算，但最终目的是用它的思想方法、获得的经验解决更多的问题，达到经验的迁移、能力的提升，从而学以致用、学有所用.故小结思考处，也是延伸处，让学生主动发现问题、提出问题、分析问题、解决问题.此处是对整节课学习的一个提升.

三、教学反思

1.以活动为主线

“链条式”课堂教学，倡导课堂上每个环节都紧密相连，层层递进，问题、追问一气呵成.笔者认为“链条式”课堂呈现方式最重要的一部分就是以活动为主线，通过多个活动的探索，引导学生积极思考、大胆探索，最大幅度地调动起学生，从而积极参与课堂教学的每一个活动.

纵观本节课，有1个数学背景的情境，2个数学内部的活动，情境从幂的意义入手，从具体的数逐渐抽象成字母，从而得出结论.这部分的设计一气呵成，每个环节都为下个环节做了很好的铺垫.

课堂上，我们一定要坚信，只有让学生主动思考、积极参与，学生学习数学的热情才会逐渐高涨，创造力才会逐渐加强.所以在本节课上，每一个活动中笔者都尽可能让学生自己去说、去做、去感悟、去归纳，最终概念自然生成，这就是“润物细无声”的境界.

2.以能力为归宿

“链条式”课堂教学，提倡课堂上

每个环节都引发深思，层层递进，最终一节课学有收获.笔者认为“链条式”课堂最终目标应是学生能力的提高，通过多个问题的探索，引导学生积极寻找问题中的规律，最大幅度地让学生大胆说出自己的想法，从而对知识有更深层次的理解.

本节课在同底数幂的乘法法则得出后，先是简单的两个例题，例1四个题目的选择有一定的必然性，包含了多种类型的同底数幂的乘法，可以发现学生存在的障碍，接着研究生活中的问题，强化学生对知识的理解及提高解决问题的能力，继而拓展，在练习二研究3个同底数幂的乘法运算，第（1）题让学生了解到有时候计算时底数不同，不能用同底数幂的乘法法则，要想办法转化，第（2）题让学生了解到同底数幂的乘法法则当底数为多项式时仍然适用，第（3）题让学生了解到计算时有时会出现多个同底数幂相乘的情况，要想办法得到更为一般的结论.层层递进的设计，难度不断升级，学生的理解也逐步深刻，在无形中使学生对本节课的理解达到巅峰.

“链条式”课堂，别样精彩，此法优化了教学的结构，也提高了教学的质量.然则任何模式的背后都有值得思考、改进的地方，更需用智慧不断完善.