基于RBF+NTSMC的舰载火箭炮随动系统控制研究

项 军，陈机林，侯远龙，王经纬，王 明

(南京理工大学 机械工程学院，江苏 南京 210094)

火箭炮在发射时,受到如负载瞬间变化大、燃气流冲击等强干扰影响，会导致定向管产生振动。在此工况下，导致系统的某些参数的不确定性，影响了火箭炮射速、跟踪精度等性能指标,使后续火箭弹发射精度降低[1-2]。因此，研究针对火箭炮系统性能提高的控制策略，是增强火箭炮系统的发射精度的有效途径。

滑模变结构对控制系统具有很强的鲁棒性，对控制系统参数摄动、外部干扰具有不变性[3]。但传统线性滑模存在问题：使系统状态逐渐趋近于给定轨迹, 但却永久无法达到给定的轨迹。文献[4]提出了非奇异终端滑模控制(non-singular terminal sliding mode control，NTSMC)这一概念。相对于线性滑模，NTSMC具有能够在有限时间收敛、跟踪精度高等优点[5]。但为了提高NTSMC快速响应以及系统的鲁棒性，文献[6]采用非线性扰动观测器和NTSMC结合的控制策略。文献[7]在指数趋近律基础上，结合了Terminal吸引子与系统状态变量的幂函数，但幂函数增加了控制的复杂性。

RBF神经网络对非线性系统具有很强大的映射能力[8]。依据RBF神经网络的逼近特性，可逼近被控对象模型的未知参数。将RBF神经网络和NTSMC策略结合起来，使系统对参数摄动和鲁棒性有所提高[9]。笔者针对舰载火箭炮交流伺服系统进行数学建模，并对基于RBF神经网络的NTSMC进行模型设计和数值仿真。为舰载火箭炮系统非线性补偿提供了一种解决方案，且实现算法较为简单，仿真及台架实验都取得了良好的控制效果。

1 系统组成及数学模型的建立

1.1 系统组成及工作原理

舰载火箭炮系统框架如图1所示。该系统是由火控系统控制箱、伺服放大器、D/A转换器、旋转变压器、RDC模块等构成。

系统执行流程：舰载火箭炮系统是一种机电结合的火控系统，上位机给出方向和高低角度，控制箱计算出当前控制信号，并由D/A模块转变成数字量信号，伺服放大器对数字量信号放大处理。然后传送到驱动器中，并依据速度反馈来调节电机转速。最后，经过减速器把机械动力传递给发射架。发射架的实际位置通过高精度旋转变压器采集位置信号，再由RDC转换模块转换后，反馈到火控系统控制箱中。

1.2 系统模型建立

舰载火箭炮交流伺服系统可简化为一个二阶系统，控制器将位置误差换算成一个对应于电机理想转速的电压值，然后传递给放大器。其系统框图如图2所示。

图2中：θref为设定的目标位置(角度)；θ为负载当前角度位置；U为控制电压；Ka为放大器增益(含功率放大器)；L为电枢回路电感；R为电枢回路电阻；Ea为电机电枢反电动势；Kt为转矩系数；Te为执行电机电磁转矩；TL为负载扰动力矩；J为电机转子上的总转动惯量；B为粘性摩擦系数；ωm为电机角速度；Ke为执行电机的反电动势系数；i为减速比。

根据伺服系统结构框图2知，执行电机电磁转矩为：

(1)

根据系统框图，由机械运动方程可得：

(2)

将式(1)带入式(2)式得：

(3)

式(3)两边同乘以1/Ji，并整理得：

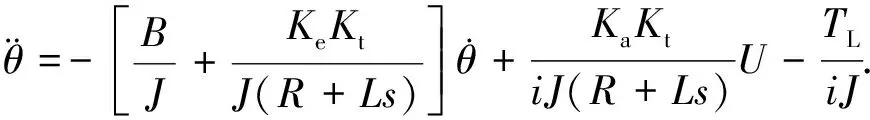
(4)

电机在执行过程中，其电流时间常数远小于机械时间常数。因此，可忽略电流响应的延迟时间，即：

(5)

式(4)进一步化简为

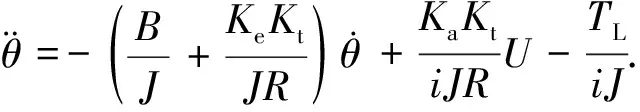
(6)

(7)

2 基于RBF+NTSMC设计

2.1 非奇异终端滑模控制器

为了使控制系统能够提高火箭炮的射速以及跟踪精度，因此控制器滑模面被设计为非奇异终端滑模[10]，其表达形式:

(8)

式中，p和q为正奇数并满足1

针对式(7)的非线性系统,设计一种自适应变速指数趋近律：

(9)

式中：k>0;ε>0;c>0.

设计控制律：

(10)

2.2 RBF神经网络控制设计

RBF神经网络结构如图3所示，其采用2-7-1的3层神经网络架构，即输入层含有2个变量，隐含层为7个神经元节点，输出层输出uRBF.

1)第1层：采用向量矩阵x=[x1,x2]T作为该神经网络的输入层参数。

2)第2层：作为隐含层，高斯函数作为其基函数，设计了7个神经元节点，即h=[h0,h1,…,h6]T.

(11)

式中：j为网络隐含层第j个网络输入；cj为基函数的宽度；bj为基函数的中心。

3)第3层：作为输出层，即输出uRBF,向量W=[w0,w1,…,w6]是隐含层和输出层之间的权值，由图3可知：

(12)

RBF网络输入输出算法为[11]：

f(x)=W*Thf(x)+εf，

(13)

g(x)=V*Thg(x)+εg，

(14)

式中:W*和V*分别为逼近f(x)和g(x)的理想网络权值；εf和εg均为网络逼近误差值，|εf|≤εMf，|εg|≤εMg.

取x=[x1,x2]T，则RBF输出为：

(15)

(16)

式中，hf(x)和hg(x)为RBF网络的高斯基函数。

上述式中出现的f(x,t)和g(x,t)均为未知参数，采取RBF神经网络去逼近未知量f(x,t)和g(x,t).

经过RBF网络逼近后，式(10)的控制律变为：

(17)

2.3 基于RBF神经网络的NTSMC控制器设计

综上可知，设计基于RBF神经网络的NTSMC系统框图如图4所示。

3 基于RBF+NTSMC稳定性分析

设计Lyapunov函数为：

(18)

(19)

(20)

将(20)式代入(19)式得：

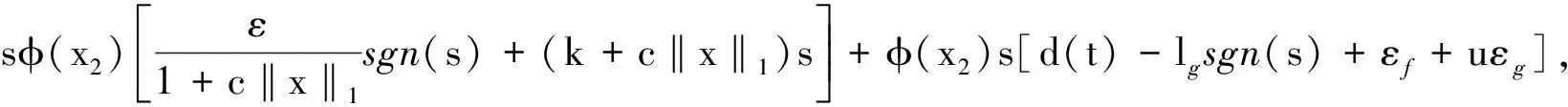
(21)

故取自适应律为：

(22)

(23)

则可得:

(24)

4 仿真分析

仿真中要用到的主要参数：R=0.4 Ω，J=5 239 kg·m2，TL=9.32 kN·m，i=1 039，p=9,q=7,B=1.43×10-4N·m/(rad·s-1),Kt=0.195 N·m/A，Ke=0.197 V/(rad·s-1).已知式(22)～(23)以及 (17)中的参数：γ1=10，γ2=1.0，ε=10，k=2,c=5，β=5.

为了突显本文提出的控制方法的有效性。仿真比较NTSMC和基于RBF神经网络的NTSMC在舰载火箭炮系统中控制效果上的差异。

设定目标角度为20°，仿真时间为10 s,阶跃响应曲线如图5所示。

从图5中可知：传统的NTSMC和基于RBF神经网络的NTSMC均无超调。但传统的NTSMC，其响应时间达到了2.1 s，而基于RBF神经网络的NTSMC，响应时间仅为1.2 s，比NTSMC约快了1倍。这表明基于RBF神经网络的NTSMC系统具有更快的响应速度，有利于火箭炮系统的快速跟踪。传统的NTSMC，其稳态误差为0.09°，而基于RBF神经网络的NTSMC，最终跟踪稳态误差只有0.03°，远小于传统NTSMC的稳态误差，表明基于RBF神经网络的NTSMC系统性能更好，有利于火箭炮精确发射。

负载扰动的阶跃响应曲线如图6所示，6.5 s时在负载上间隔0.4 s加载负载，形成脉冲力矩来模拟火箭炮发射时的冲击载荷。从图中可知：采用基于RBF神经网络的NTSMC，系统产生的偏移较小，且能够更快地恢复到目标位置，因此提出的控制方法抗干扰能力强。

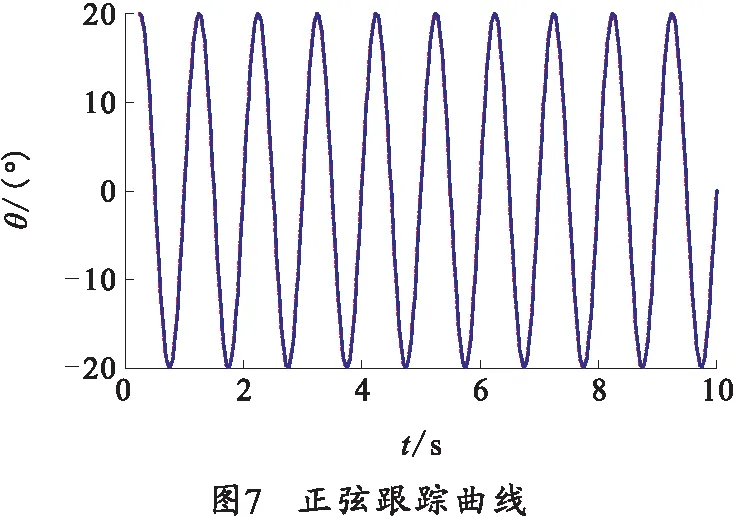
输入信号y(t)=20 sin(2πt)，幅值为20°，周期为1 s，仿真时间为 10 s,正弦跟踪及误差仿真曲线如图7、8所示。控制策略采用基于RBF神经网络的NTSMC方法，尽管系统未稳定时正弦追踪误差较大，最高峰值达到0.15°，但其迅速调整并进入良好的跟踪状态，最终的误差范围保持在±0.055°，满足火箭炮发射精度的要求；当控制算法采用传统的NTSMC时，起始的最大误差为±0.4°，经过一段时间的调整后其最终的误差范围在±0.14°内，严重不符合火箭炮精度要求。由此可知，控制策略采用基于RBF神经网络的NTSMC能有效提高系统跟踪能力、保持较好的鲁棒性以及提高了火箭炮发射精度。

5 结束语

针对系统中存在的火箭炮射速、跟踪精度问题，提出基于RBF神经网络的NTSMC控制策略。结合了NTSMC在非线性系统中的优越性和RBF神经网络良好的逼近性能，这样既保持了基本滑模控制强鲁棒性的优点,同时，使系统响应速度快，提高跟踪精度，具有良好的动静态性能，使火箭炮能够精准发射。仿真结果进一步验证了基于RBF神经网络的NTSMC的有效性，能够很好地提高舰载火箭炮系统的控制性能。