多边时滞脉冲反馈方法控制SAS的混沌与降低损失率

陈 明，朱学帅

(1.湖北中医药高等专科学校公共基础部，湖北 荆州 434020；2.中国矿业大学(北京)化学与环境工程学院，北京 100083)

0 引言

开关流系统(switched flow system,SFS)[1]是一种典型的混合系统，分为开关到达系统(switched arrival system,SAS)[1-3]和开关服务系统(switched service system,SSS)两类。SAS具有广泛的工程背景，常用来研究复杂工业控制系统。混沌运动[3]是一种无法精确重复、貌似随机的运动。由于混沌运动的不确定性，多数情况下应该抑制混沌运动的产生。SAS在某些情况下会产生混沌现象，且系统本身存在周期轨[4-5]。为此，以周期轨为控制目标，实施多边时滞脉冲反馈方法[5-7]来控制SAS中混沌现象，但该方法是基于开关时间[1,2,5]为0的情况。而实际工业控制中，开关时间一般大于0。此时系统不仅有混沌现象，还会产生系统损失。为此对多边时滞脉冲反馈方法加以改进[8-12]，使其既能控制SAS中混沌现象，又能降低系统的损失率,同时还能探测目标周期轨道。

1 开关到达系统与系统损失

1.1 开关到达系统数学模型与开关时间

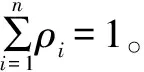
服务器切换方法：当某缓冲器i量值为0，服务器当即转到缓冲器i上进原料，设{tn}是服务器在缓冲器之间转换的时间序列。根据服务器切换方法，可得:

(1)

当t∈[tn、tn+1),服务器正向缓冲器q(tn)进原料，而xi(t)为:

(2)

当n=3时，开关到达系统如图1所示。

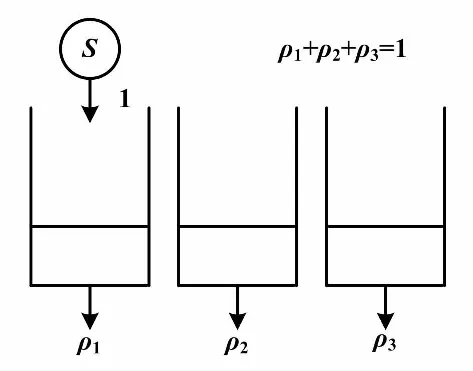
图1 开关到达系统(n=3)

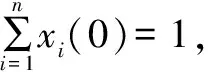
假设服务器从某个缓冲器转换到另外一个缓冲器所需要的时间为开关时间，而服务器在缓冲器之间来回切换则为开关事件。上述开关时间是忽略不计的，即开关时间为0。而实际工业生产控制中，服务器在缓冲器之间切换是需要时间的，且有时不可避免或有意为之。为了更加接近工业生产控制实际，下文将系统开关时间设为定值λ>0。为便于论述以及数值模拟，不失一般性，以n=3为例。

1.2 开关时间大于0时系统损失

系统损失是指缓冲器在某一时间段内因产出速度为0，使系统整体产出小于1，以降低生产效率。已知开关时间λ>0,{tn}为服务器在缓冲器之间切换的时间序列。两种情况下，系统产生损失。首先，根据SAS中服务器切换方法可知，当t=tn时，系统中某个缓冲器排空，服务器并不能立即切换该缓冲器，而是继续向以前选定的缓冲器进入，直到t=tn+λ时，服务器才切换到空缓冲器上。而此时间段(t∈[tn,tn+λ])因空缓冲器存在，使该缓冲器产出速度变为0而导致系统产出速度减少，因而系统产生损失。再则，当已有一个缓冲器排空时，会出现另一个缓冲器也排空情况。假定t=tn+γ(0<γ<λ)时，又一个缓冲器排空，则服务器首先在t=tn+λ时切换到首先排空的缓冲器上，接着在t=tn+λ+γ时切换到其次排空的缓冲器上。在t∈[tn,tn+γ]和t∈[tn+λ,tn+λ+γ)这两个时间段内，系统有一个空缓冲器存在；在t∈[tn+γ,tn+λ)这个时间段内系统有两个空缓冲器存在，由于空缓冲器产出速度为0而导致系统产生损失。为保持系统动态平衡，这些时间段内的服务器进入速度要减少到与系统产出速度相等。基于系统轨线运行区域S描述，系统轨线会沿着某个边界滑动γ时间后到达某个顶点，驻留时间λ-γ后，继续沿着另一个边界滑动γ时间后离开该边界。

2 开关时间大于0时多边时滞脉冲反馈控制

2.1 多边时滞脉冲反馈控制

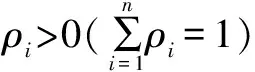
(3)

式中：α为存在且能改变的控制系数。

此方法优点是不需要确定目标周期轨具体位置，反而能够探测到周期轨具体位置。

2.2 开关时间大于0时控制方法的改变

开关时间大于0时，系统会产生损失，所以降低开关事件的发生次数来降低损失率是可行的，同时还要控制系统混沌现象。该方法的改变是对实施控制时间进行选择，以避免在实施控制时发生开关事件，并且选定1-周期轨为控制目标，即设m=1。

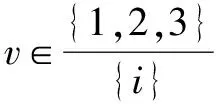
(4)

显然{θni}是从{θni}选出的子序列，即有{θki}⊂{θni}，而第ki次控制量大小为:

(5)

因此，第ki次控制结束时间为:

(6)

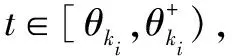
控制时间的改变不仅可以避免在控制时间内开关事件的发生，而且也不影响该方法的有效性，既能够降低系统损失率，又能够控制系统混沌现象。

2.3 周期轨道

选择系统轨线运行区域的某个边界Si作为庞加莱截面(Poincare section,PS)[2,5]。采用系统轨线在不同时间到达此边界的具体位置来研究轨线的运行规律，并以此来定义周期轨道。

设{θni}为系统轨线x(t)第ni次到达某边界Si的时间序列，若有：

x(θni)=x(θni+m)

(7)

则边界Si定义下的以m为周期的周期轨道，记为per[x(t)|Si]=m。

但是选定不同的边界作为庞加莱截面，得到周期轨的周期可能不同。进一步定义为：

(8)

SAS系统以m为周期的周期轨，记为m-周期轨。

3 数值验证

3.1 混沌控制与损失率比较

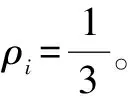
设系统初始值x=[0 0.25 0.75]T，开关时间为λ=0.2和λ=0.3时，α=0.95，以1-周期轨道为控制目标，模拟有无施加控制情况下系统轨线分别如图2、图3所示。施加控制后不仅消除了混沌现象，而且将系统轨线稳定到1-周期轨道上。

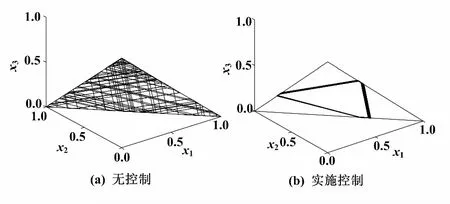
图2 有无施加控制的系统轨线(λ=0.2)

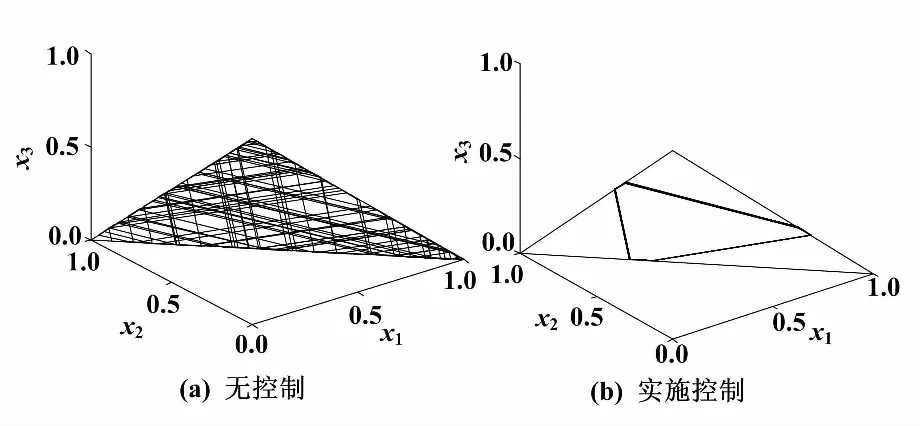
图3 有无施加控制的系统轨线(λ=0.3)

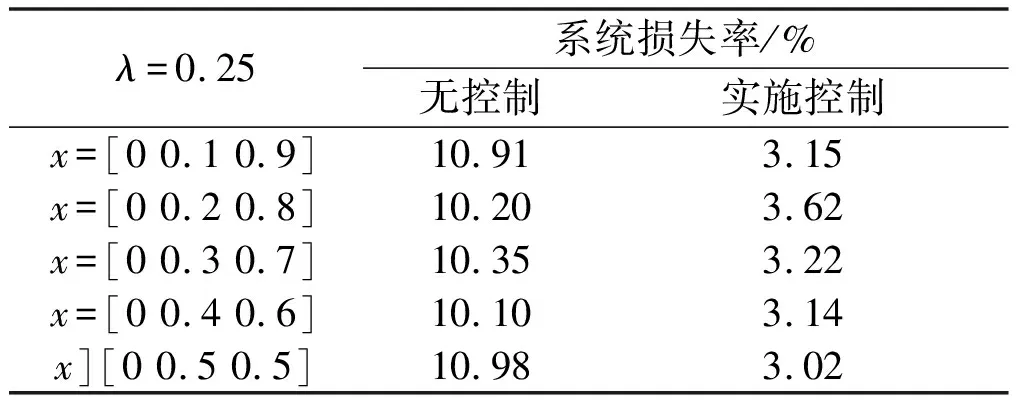
表1 有无施加控制的系统损失率

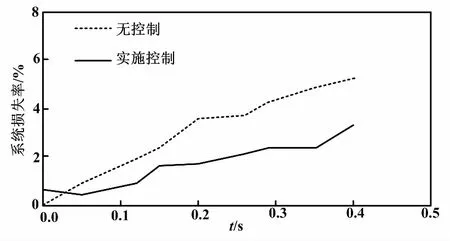
图4 有无施加控制的系统损失率曲线

3.2 周期轨道探测

取系统初始值x=[0 0.28 0.8]T，开关时间为λ=0、0.25时，分别模拟有无开关时间情况下1-周期轨线，如图5、图6所示。注意到当开关时间存在时，周期轨道在系统边界上滑动过程对应为开关事件，时间上则对应于开关时间。

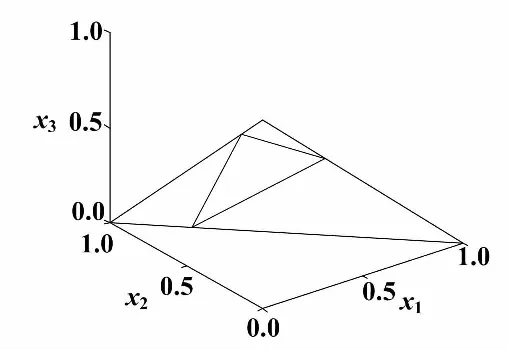
图5 1-周期轨道(λ=0)

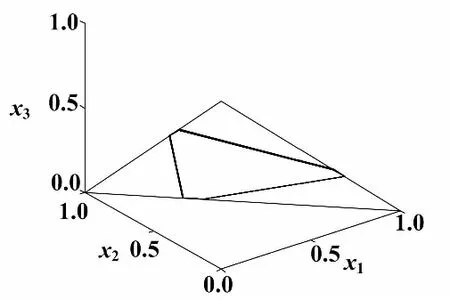
图6 1-周期轨道(λ=0.25)

4 结束语

针对更接近工业生产实际的开关时间大于0的SAS，时滞脉冲反馈控制方法优点是不需要预先知道目标周期轨，反而能探测周期轨。改进后的多边时滞脉冲控制方法不仅可以抑制系统混沌现象，还能有效降低系统损失，同时探测周期轨道。因此，该方法应用于工业生产实际中，可以提高生产效率，具有广泛的实效性、推广性和移植性。