基于工况划分的火电机组运行多目标优化

叶灵芝，贾 立，宋鸣程

(上海大学机电工程与自动化学院，上海 200072)

0 引言

火电机组运行优化是提高热力设备甚至整个电厂效率的重要手段。运行优化的目标值反映了当前工况下机组所能达到的最佳参数，为操作人员提供了重要的指导信息[1-2]。然而，在实际运行过程中，国内电站机组普遍存在负荷和工况变化大的问题[3]；同时，运行优化的目标也根据实际需求不同而变化。在机组运行优化过程中，机组的运行效率和降低污染物排放的最优解相互冲突，提高电站机组效率常常以牺牲环境为代价[4]。

本文研究了基于工况划分的火电机组运行多目标优化问题，提出改进的K-means算法，对电站历史数据进行工况划分，并采用多目标优化方法协调电厂经济指标与环保指标的冲突问题。该方法对电厂实际运行操作具有一定的指导意义。

1 基于改进K-means算法的工况划分

火电厂积累了大量的历史运行数据，采用工况划分的数据挖掘方法提取电厂的运行规则，其中常用K-means聚类算法进行划分。传统的K-means算法具有简单、快速的优点，但也存在一些缺点。不少学者都提出了优化方法，但在实际的工况划分中仍存在一些问题。

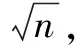
定义评价准则函数为：

(1)

式中：xij为第i类的第j个数据；ni为第i类的数据个数；mi为第i类的中心；xlr为第l类的第r个数据；nl为第l类的数据个数。

即式(1)中：分子为类内数据与该类中心的距离之和，表示类内的紧密度；分母为类外数据与该类中心的距离之和，表示不同类间的分散度。该比值越小，代表类内数据越集中，不同类间的数据越分散，划分越合理。

为根据评价准则函数得到聚类数为10左右的局部最优值，其具体选择步骤如下。

①选择初值k=n(n<10)。

②对所有数据进行聚类，得到所有聚类中心mi(i=1,2,…,k)以及类内数据xij(i=1,2,…,k;j=1,2,…,ni)。

③根据式(1)计算Gn(k)。

④k=n+1，重复步骤②，根据式(1)计算Gn+1(k)。

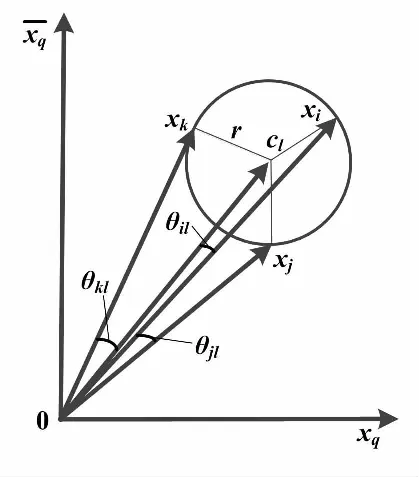
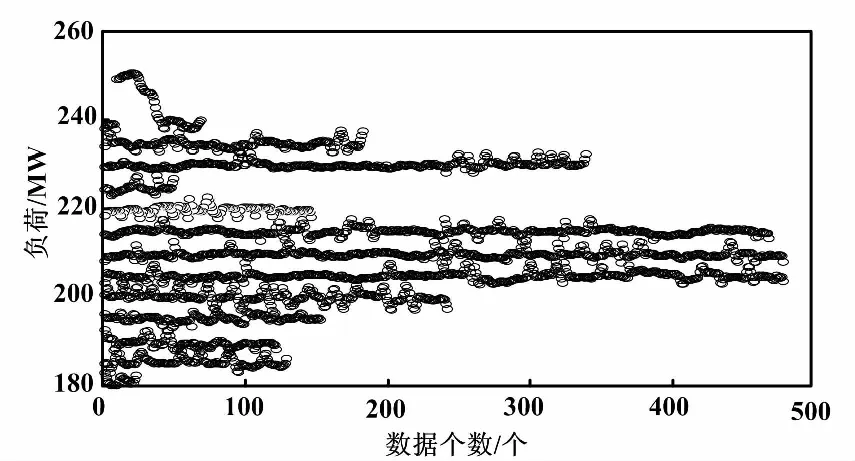
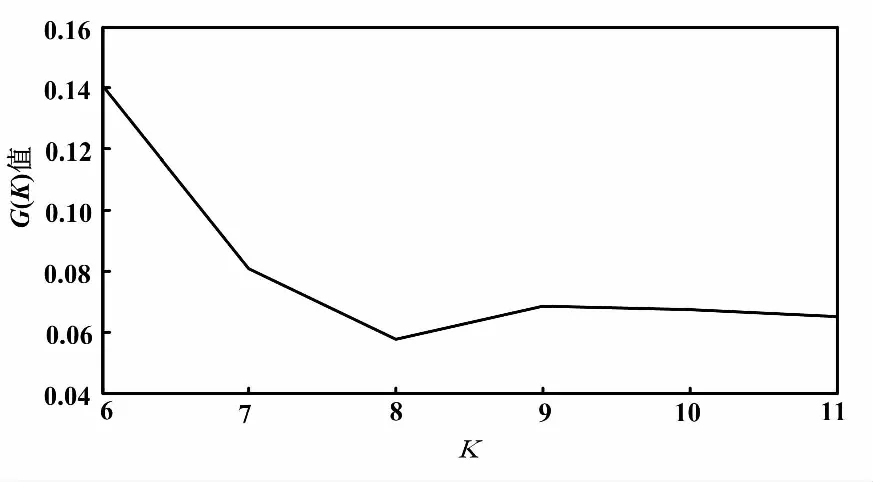
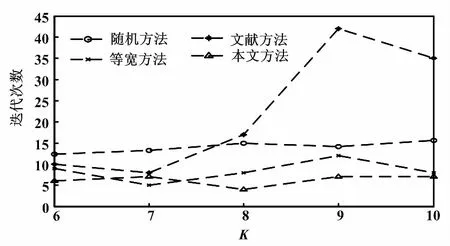
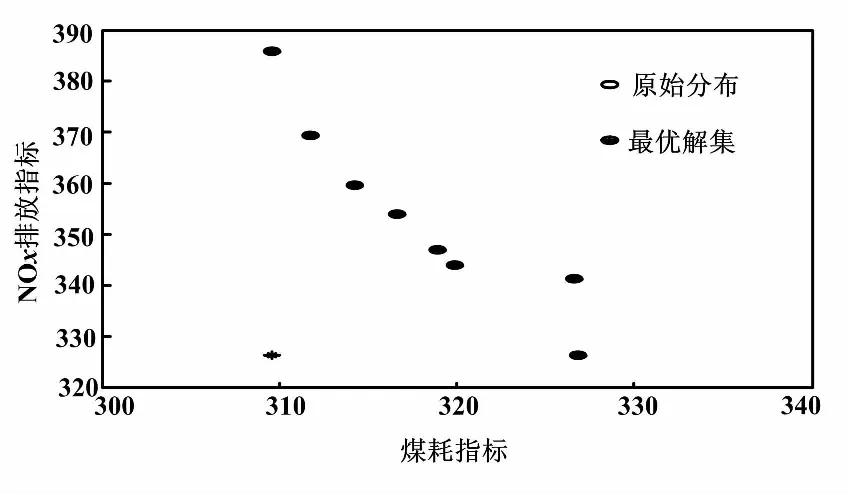
⑤若Gn(k)>Gn+1(k)，重复步骤③、④得到Gn+2(k)；若Gn+1(k)

在算法中需要根据初始聚类中心来确定一个初始划分，然后对初始划分进行优化。初始聚类中心的选取对聚类结果有较大的影响。针对该缺点，许多学者进行研究，也提出了不同的优化方法。一般这些优化算法都应用于二维及以上的数据进行聚类，而电厂机组的工况划分是一种一维数据的划分，许多优化算法并不适用，会出现各种问题。文献[8]提出了根据距离最大的方法寻找初始聚类中心，但在实际工况划分中得到的初始聚类中心分布在极值两端，使迭代次数过大，结果分布不合理。文献[9]提出了基于密度的方法，能够获得密度较高的初始聚类中心，但该方法的时间复杂度大，对于数据量大的聚类而言，计算缓慢。

因此，本文借鉴基于密度的思想，提出了一种适用于工况划分的基于数据分布的初始聚类中心优化方法。在所有数据中，找到数据分布最集中的前K个数据簇，将这些数据簇的中心点作为初始聚类中心。具体步骤如下。

①从第1个数据开始，找到与第1个数据距离最小的数据xj,将数据xj作为中心，把所有与数据xj距离小于d的数据划分为第j类，并计算第j类的类内数据个数nj。

②对第i个数据，在未分类数据中找到与数据xi距离最小的数据xl，将数据xl作为中心，把所有与数据xl距离小于d的未分类数据划分为第l类，计算第l类的类内数据个数nl。

③重复步骤②，直到所有数据都被分类标记。

④对所有类包含的数据个数n进行排序，找到K个包含数据最多的类，输出对应的类中心，作为初始的聚类中心。

文献[9]提出的密度估计方法的时间复杂度为O(N2m2)。其中，N是所需划分的数据量大小，m是确定密度参数的指定数，数据量越大，m取值越大。本文提出的方法的时间复杂度为O(N2)。当数据量越大，本文所提出的方法速度优势越明显，越能有效地提高计算效率。

采用改进的K-means算法对机组的负荷、煤质情况及外界温度进行工况划分，得到包含相似运行工况的不同工况簇。因此，我们可以对这些工况簇进行挖掘，得到每一类相似运行工况下的运行最优目标值，以指导电厂实时操作运行。

2 基于角度-距离相似度的多目标优化

机组运行优化目标值是一种典型的机组运行性能状态空间多维约束寻优问题，是在指定工况下，机组运行参数应达到的最佳值。火电厂性能指标计算和分析的具体内容是指计算当前工况下机组的一些重要指标的实时值。常用的性能指标有稳定性、经济性、环保性和综合性。

火电厂主要通过电厂水耗、发电标煤耗、锅炉效率指标等来表示机组的经济性。随着国家对火电厂排放标准的提高，烟尘、SO2、NOx等污染物的排放也需要同时考虑。但是环保性和经济性存在冲突，例如降低NOx排放浓度会影响锅炉的燃烧效率[10]。因此，需要采用多目标优化的方法来进行协调。根据实际的电厂数据以及计算的复杂程度，本文主要考虑以发电煤耗为经济性指标和以NOx排放浓度为环保性指标的多目标问题。

对于多目标优化问题，许多学者已经进行了研究，并取得了一定的成果。如文献[11]提出了交互式的多种群遗传算法，解决电力系统的经济负荷分配问题；文献[12]提出了改进的遗传算法与理想点法结合的方法，优化火电厂污染物的排放；文献[13]使用了NSGA-Ⅱ方法和理想点法结合的多目标择优方法，能够更有效、合理地得到多目标的最优解。

在理想点法中，通常采用欧氏距离进行相似度分析。但仿真结果表明，角度信息对最优解的选择也有着重要的影响。借鉴NSGA-Ⅱ和理想点法结合的思想，本文首先采用NSGA-Ⅱ方法对电厂经济性和环保性的双目标问题进行多目标寻优，获得一组非支配解。然后，采用理想点法结合角度-距离的相似度度量方式，在得到的非支配集合中选择最优解，以此来指导电厂的实际操作。角度-距离相似度度量方式如图1所示。

图1 角度-距离相似度度量方式

角度-距离的相似度度量公式为：

(2)

式中：d(xi,xq)为xi与xq的欧氏距离。

(3)

式中：γ∈(0,1)为介于0和1之间权重参数；σ为xi和xq的二次范数；θi,q为点xi与xq的角度。

(4)

3 实例应用与分析

本文选取了某电厂300 MV机组某月10天的机组运行工况数据进行试验。在这一段时间内，环境温度变化较小，机组没有明显表征出在温度变化时的特征变化，故只采用机组负荷、煤质情况对机组运行工况进行划分。然后对划分后的每一工况进行经济性和环保性的多目标优化，寻找双目标协调下的最佳运行参数以指导电厂机组实际运行。

3.1 工况划分结果

3.1.1 负荷划分结果

在电厂中，机组负荷的确定一般以50%、60%、70%、80%、90%、100%负荷作为运行工况参数。但在实际的操作运行中，受机组设备状态、环境条件约束等各方面影响，上述这些划分已不是常见的工况。因此，需要以机组实际经常稳定的负荷作为参数，在该参数下指导运行。这比在传统百分比表示的典型负荷下进行指导更有意义。数据原始分布如图2所示。由图2可知，负荷主要分布在205 MW、210 MW、215 MW、230 MW这几个点附近，例如机组经常稳定工作在230 MW以及235 MW，而不是传统的80%负荷(240 MW)。

图2 数据原始分布图

对电厂2 880组稳态数据进行工况划分：首先取K=6，通过最优聚类数的选择机制，确定最优聚类数为K=8。不同聚类数下的评价准则函数值如图3所示。

采用本文提出的方法获取初始聚类中心，分别在聚类数K=6、7、8、9、10下进行工况划分，并与几种常见初始聚类中心获取方法——随机选择、等宽划分和密度估计得到的划分结果进行比较。

图3 不同聚类数下的G(K)值

①每种方法在不同聚类数K下分别进行10次试验，比较不同方法在不同聚类数下的迭代次数。四种方法在聚类数K=8时的10次试验迭代次数，如图4所示。四种方法在不同聚类数下所需的平均迭代次数如图5所示。

图4 四种方法在K=8时的迭代次数

图5 四种方法在不同聚类数K的平均迭代次数

由图4可以看出，除了随机获取初始聚类中心的方法具有偶然性，故每次的迭代次数都不同，而其他几种方法所需的迭代次数比较稳定。但是文献所提出的方法迭代次数远大于等宽选取和本文提出的方法。从图5可以得到，四种方法在不同的聚类数下，所需的迭代次数也不同，尤其文献所提方法在聚类数变大时迭代次数变化幅度较大。

总体而言，等宽选取初始聚类中心的方法和本文提出的方法要优于其他两种方法，但本文提出的方法所需的迭代次数总体上更少，尤其在最优聚类数K=8时，本文提出的方法迭代次数最少。根据K-means算法近于线性的时间复杂度O(NKt)(N是所需划分的数据量大小，t是迭代的次数)，在同样数据量和聚类数下，迭代次数越少，划分所需的时间也越少。

②不同的初始聚类中心及不同的初始聚类中心选取方法在聚类数K=8时进行划分，得到了不同的划分结果。随机获取初始中心得到的划分结果有较大区别，结果不稳定，并且会存在划分结果不合理的情况。对比等宽选取的划分结果、本文方法得到的划分结果与原始数据分布，本文方法得到的划分结果更详细地划分了分布较密集的工况区间，比如负荷分布为195 MW和200 MW左右，这更利于对每一工况进行分析，划分结果更合理。

综上可以看出，对比等宽划分、随机选择和密度选取这三种获得初始聚类中心的方法，本文提出的方法计算更快速、高效，划分结果更合理。

3.1.2 煤质划分结果

煤质系数为：

(5)

式中：Ne为机组负荷；Ff为同一时刻的给煤量。

采用本文提出的优化初始聚类中心算法，把煤质系数分为好、中、差三类分类结果。

3.2 多目标优化结果

煤质系数划分结果如表1所示。 对每一个工况进行运行优化规则提取：以稳定工况的负荷区间为[197.826，202.484]、煤质系数中等的166组数据为例进行分析。优化指标选择综合性指标即同时考虑经济性和环保性。其中，经济性选择发电煤耗，环保性选择NOX排放量。考虑与发电煤耗和NOX排放量相关系数大的运行参数作为运行指导的目标参数[14]，如主蒸汽压力、总风量、给煤机给煤量、空预器出口烟温、烟气含氧量等。指定工况下的运行参数值及性能指标见表2。

表1 煤质系数划分结果

表2 指定工况的运行参数及性能指标

首先，采用NSGA-Ⅱ方法获得一组最优解集，对比原始分布，得到的每一个最优解都为非支配解，分布在数据的前沿，可以按不同的选择指标确定为唯一最优解。指标原始分布和最优解集对比如图6所示。

图6 指标原始分布和最优解集对比图

然后，采用理想点法并根据新相似度测度方法，在已得到的一组最优解集中求取最优解。理想点法对比如图8所示。

图7 理想点法对比图

最优目标值对应的各运行参数如表3所示。

表3 最优目标值对应的各运行参数

4 结束语

本文提出了一种基于改进的K-means算法进行工况划分的火电机组运行多目标优化方法。该算法首先通过数据分布来改善K-means算法的初始聚类中心选取，并通过评价准则函数确定最优聚类数，使工况划分结果更加合理。其次将NSGA-Ⅱ与理想点法结合，并使用角度-距离相似度度量方法，协调发电煤耗和NOX排放量两者冲突的问题。试验证明，本文提出的算法更快速、高效、详细，能有效地指导电厂在低煤耗和低NOX排放下运行，具有一定的实际应用价值。