基于稳定性演化路径的反倾斜坡变形演化特征研究

谢良甫，张佳琪，谭顺利，王 博

(新疆大学建筑工程学院，新疆乌鲁木齐830046)

0 引 言

一般认为，反倾斜坡稳定性较好，不易产生贯通性的滑面，因而对其关注度远不如顺层斜坡。然而，随着人类工程活动范围的不断扩大，此类边坡的稳定性问题不断凸显，且发育规模巨大，严重威胁着工程建设[1]。大量工程案例表明，反倾岩质斜坡变形破坏的一个典型特征是其弯曲折断面一般需经历较长的孕育时间，而一旦失稳，其破坏规模是巨大的，破坏程度也通常是非常剧烈的，危害相当严重[2]。因此，研究反倾斜坡长期时效变形演化特征，对反倾斜坡的防灾减灾具有重要的理论意义。

目前，对反倾边坡变形演化研究主要借助工程地质分析[3]、物理模型试验法[4-7]以及数值模拟法[8-11]。张国新等[12]采用数值流形法进行了反倾斜坡倾倒变形破坏特征的模拟，并与离心机模型试验结果进行了对比分析；任光明等[13]从河谷演化、成坡角度研究了反倾斜坡变形演化过程；罗勇和龚晓南[14]采用离散元UDEC软件进行了节理发育的反倾斜坡的变形破坏分析。这些研究成果的应用一般需要较为丰富的工程经验或较为完备的科研条件，多停留于理论层次，在实际生产项目中难以推广应用。为此，本文依托具体工程实例，选用常用的极限平衡分析法[15-19]，通过稳定性的变化研究反倾斜坡的变形演化特征，研究成果更易于应用于实践。

1 反倾斜坡稳定性系数计算方法的确定

反倾斜坡不同于一般滑坡，对其条分时必须依托现有的岩层结构面，因此各条块的边界为不规则四边形，现行规范建议的传递系数法难以准确计算稳定性系数。为此，本文选用Sarma法计算反倾斜坡稳定性系数。

Sarma法是一种基于极限平衡法的边坡稳定性系数计算方法，该方法既能够满足力的平衡，亦能满足力矩的平衡。Sarma法假定的边坡体破坏形式和力学模型见图1。图1中，E、X分别为单元条块两侧在法向与切向的作用力；T为条块底部切向作用力；U为条块所受水压力；N为条块底部支撑反力；Wi为条块自重；KcWi为Sarma法构建的一个体积力；Fi为条块所受外力。

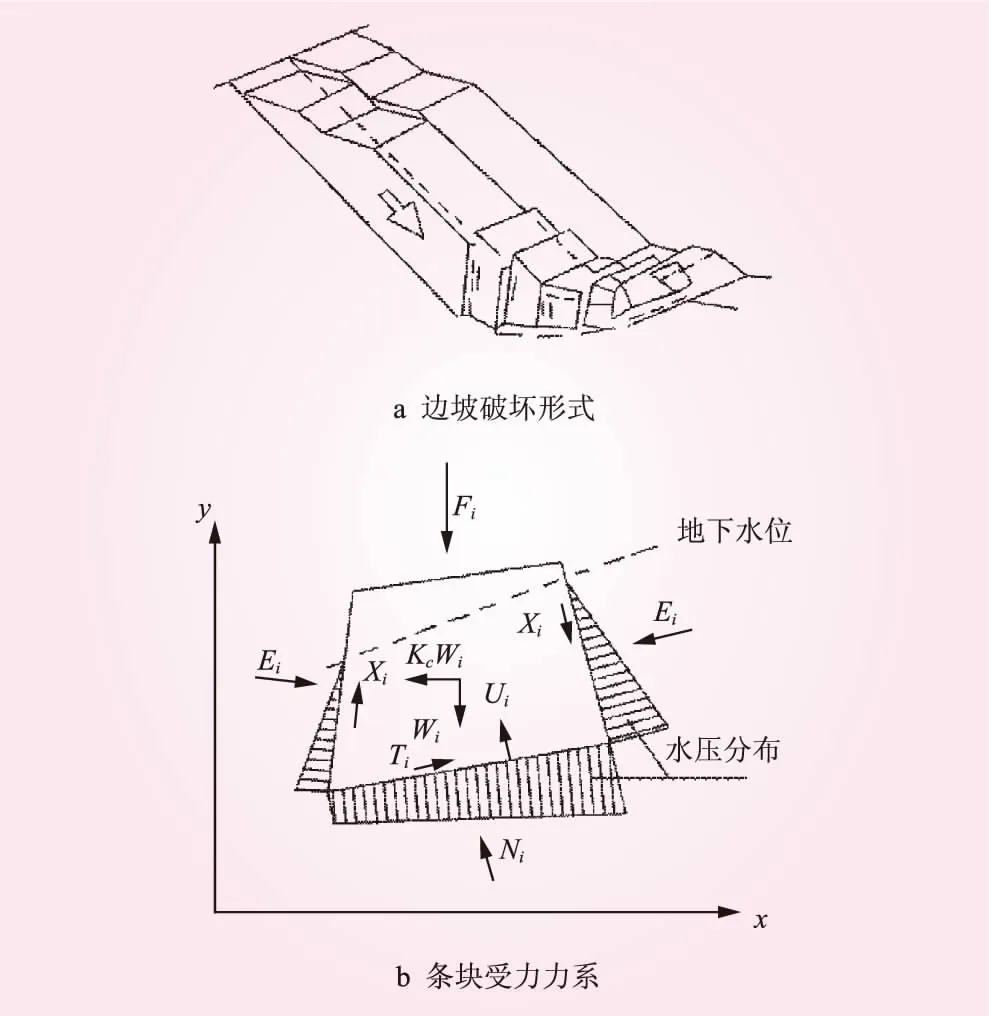
图1 Sarma法

根据条块受力分析，体积力KcWi中的Kc是边坡临界加速度系数，即ηb。假定滑坡体在该力的作用下处于极限平衡状态，分别对条块水平和铅垂线方向建立力的平衡方程得

Nicosαi+Ticosαi=Wi+Xi+1cosδi+1-Xisinδi-

Ei+1sini+1+Eisinδi

(1)

Ticosαi-Nisinαi=KcWi+Xi+1sinδi+1-Xisinδi+

Ei+1cosδi+1-Eicosδi

(2)

式中，αi为条块底面与水平方向的夹角；δi为条块左侧边界与铅垂线方向夹角。

根据摩尔-库仑破坏判据，分别对条块底部、左侧、右侧进行受力分析，有

Ti=(Ni-Ui)tanφi+ci+bisecαi

(3)

(4)

(5)

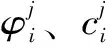
Ei+1=ai-piηb+Eiei

(6)

由于式(6)是迭代循环式，故

En+1=an-pnKc+Enen

(7)

En+1=(an+an-1en)-(pn+pn-1en)Kc+En-1enen-1

(8)

进一步迭代得

En+1=(an+an-1en+an-2enen-1+…)-Kc(pn+pn-1en+pn-2enen-1+…)+E1en-1en-2…e1

(9)

在无外荷载作用时，En+1=E1=0，故KC可表达为

Kc=(an+an-1en+an-2enen-1+…+a1enen-1…e3e2)/

(pn+pn-1en+pn-2enen-1+…+p1enen-1…e3e2)

(10)

Sarma法在斜坡稳定性系数计算过程中引入了边坡临界加速度系数Kc，在无地震动荷载作用下，可类似于强度折减法通过同时折减滑面、滑体的抗剪强度值，直至Kc趋于0，此时的折减系数即为斜坡稳定性系数。

根据Sarma法计算原理，本文采用Matlab结合CAD编制Sarma法稳定性系数计算程序，通过CAD提取各条块角点坐标和地下水位线坐标，并将坐标信息导入Matlab中，计算不同折减系数F所对应的Kc值。最后，通过Matlab中的CFtool工具进行数据拟合，取Kc=0所对应的折减值F，即斜坡的稳定性系数，见图2。

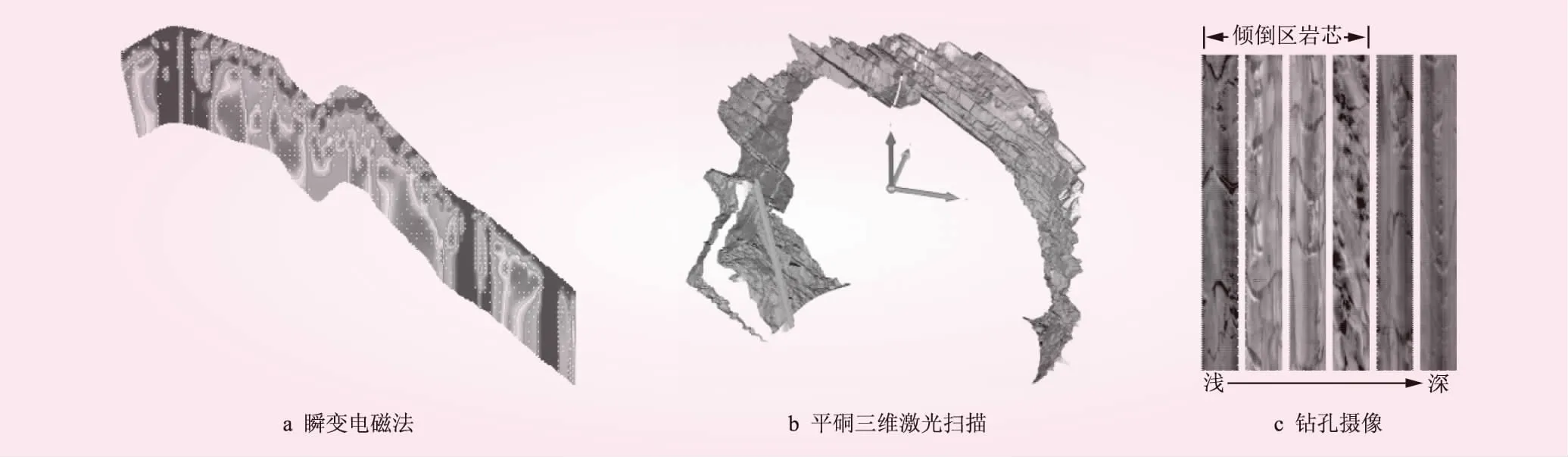
图4 勘察成果

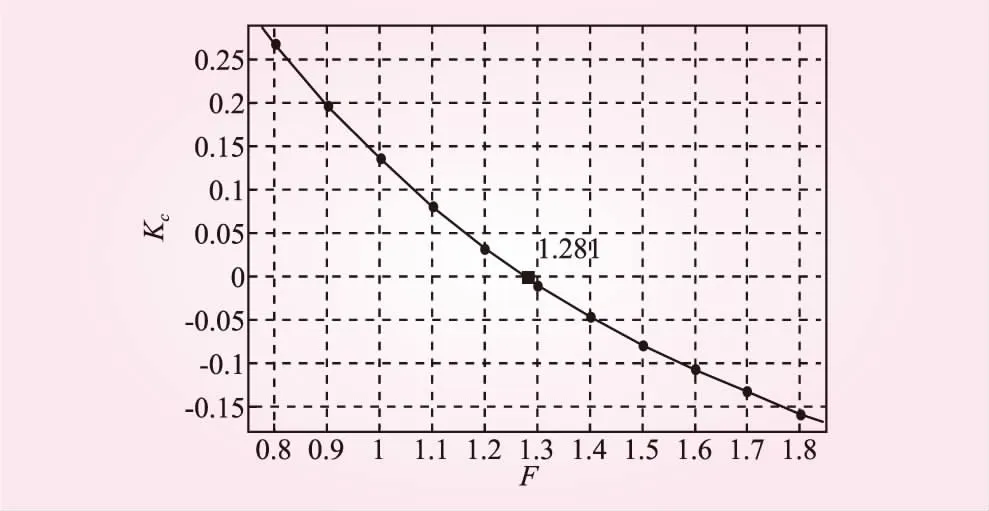
图2 稳定性系数

2 计算模型

2.1 工程概况

中梁水库斜坡位于重庆巫溪县中梁水库上游约1.2 km右岸，斜坡坡脚高程526 m、坡顶高程1 183 m，坡体宽约700 m，坡面沟谷发育，斜坡中前部坡度较陡，后部相对较缓。自水库蓄水后，斜坡体不同部位出现了较为明显的变形破坏现象。

根据现场地质调查，中梁水库斜坡为一典型反倾斜坡，斜坡体局部已发育形成一定规模的倾倒折断面，目前折断面尚未贯通，处于变形发展阶段，急需对其变形演化方向做出准确判断。中梁水库反倾斜坡变形特征见图3。

图3 反倾斜坡变形特征

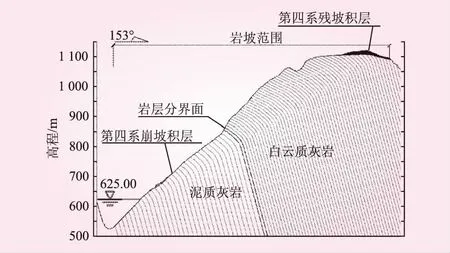
图5 反倾斜坡稳定性评价模型

2.2 模型建立及参数选取

在地表地质调查基础上，分别通过瞬变电磁法、平硐三维激光扫描、钻孔摄像等勘察成果(见图4)，获取反倾斜坡倾倒变形范围及岩层倾角随深度变化规律。选取斜坡典型纵断面(见图5)，构建斜坡稳定性评价模型。

通过现场原位直剪试验并结合室内岩石试验，获取中梁水库斜坡岩土体物理力学参数。岩体物理力学参数见表1。结构面力学参数见表2。

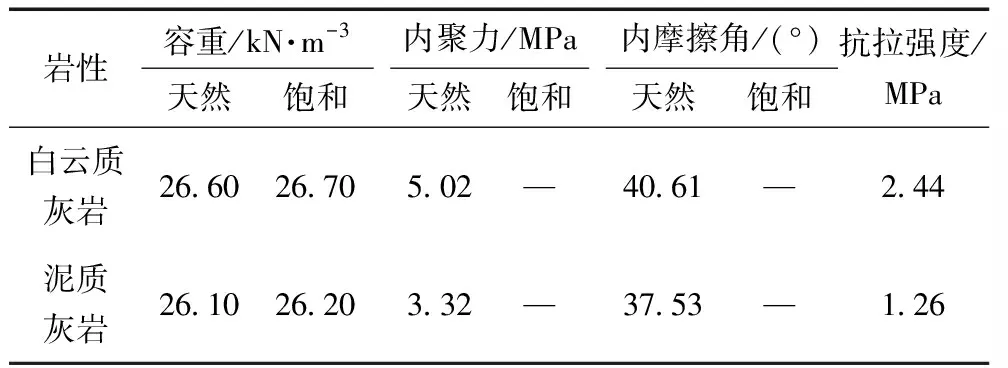
表1 岩体物理力学参数

表2 结构面力学参数

3 反倾斜坡倾倒变形分析

3.1 演化规律

反倾斜坡倾倒变形演化过程实质是稳定性降低的过程，通过分析倾倒变形稳定性演化路径能在一定程度上表征倾倒变形的演化过程。根据Goodman-Bary理论，反倾斜坡发生变形的岩层条块分为下部滑移区、中部倾倒区和上部稳定区(见图6)，图6中，ΔL为条块宽度；k为节理连通率；b为台阶高度。在倾倒变形演化过程中，稳定区条块将逐级发生倾倒成为倾倒块体，而倾倒块体倾角将进一步增大，从而提供了更大的下滑力，进而推动滑移区，使斜坡发生整体破坏。本文采用变化岩层倾倒倾角与倾倒条块数2个变量分析反倾斜坡整体稳定性系数的变化规律。

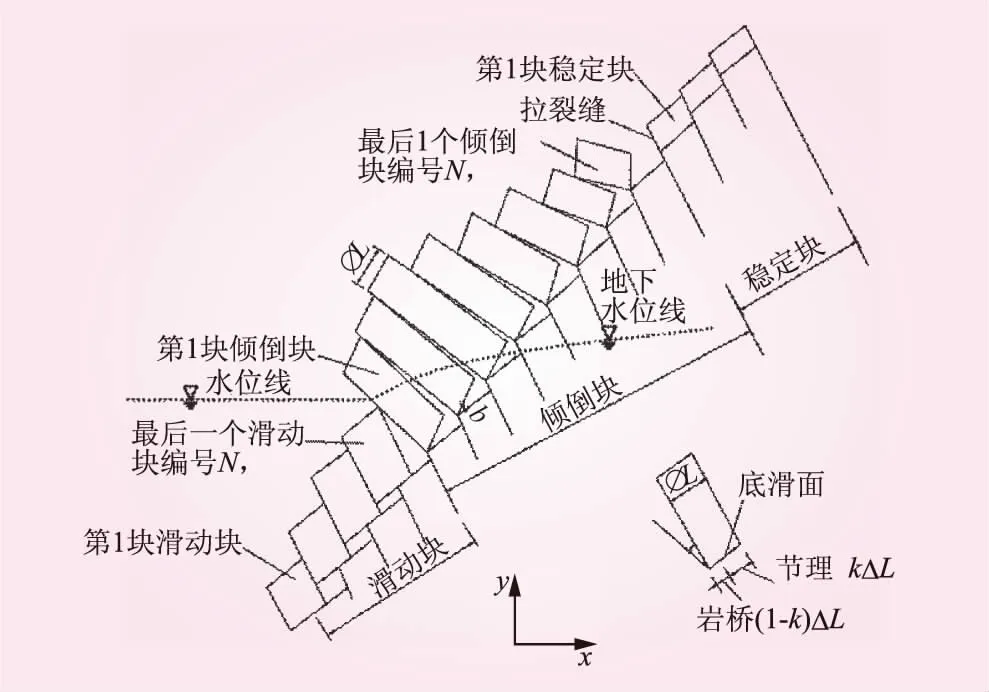
图6 反倾斜坡稳定性评价模型

无外因作用下，反倾斜坡将在自重作用下其坡体一定范围内岩层块体发生一定程度的倾倒变形。因此，在上述反倾斜坡稳定性计算程序中，通过遍历不同的倾倒条块数和倾倒角度即可得出不同组合下反倾斜坡稳定性系数，采用插值法即可得出稳定性系数云图，见图7。

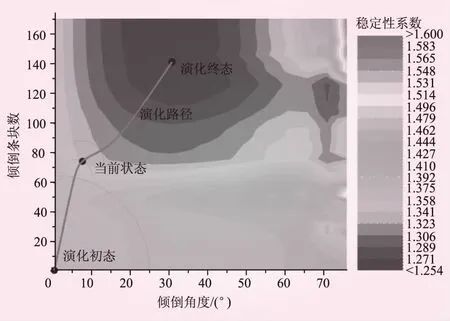
图7 斜坡倾倒变形演化路径

从图7可知，不同倾倒条块数和倾倒角度的组合下，斜坡稳定性系数主要变化范围在1.26～1.50间。倾倒条块数为120～175块、倾倒角度为20°～40°时，斜坡稳定性系数最低。斜坡倾倒变形演化初期状态为倾倒条块数为0、倾倒角度为0，即坐标原点，从系统演化的角度分析，反倾斜坡会沿坐标原点沿稳定性系数降低最快、最短的路径进入稳定性最低的区域。因此，以坐标原点为初始点，按稳定性系数降低最短路径，即可得出系统演化路径。采用Goodman-Bary法分析当前斜坡变形状态时，倾倒条块和稳定条块的分界点位于第76个条块，得出斜坡当前倾倒条块已发生约8°的偏转倾角。此时，斜坡稳定性系数已演化至路径拐点处，斜坡前期变形主要以倾倒条块数增加为主，后续演化将表现为倾倒条块数和倾倒角度同步快速增加，表明变形在加剧，稳定性加速降低。

3.2 演化路径

实际中，反倾斜坡不可避免受到外因作用而加剧其变形演化。其中，地下水是诱发边坡失稳的一个最常见也是影响较为显著的因素。因此，本文以库水作用为例，分析外因对反倾斜坡稳定性演化路径的影响。

受大坝调度库水位会发生变化，由于Sarma法中没有考虑水的动水压力，故本文将库水位视为不变简化计算。在上述研究基础上，从当前斜坡演化阶段开始加入库水作用，分析库水作用加入前后反倾斜坡稳定性演化路径的变化情况。库水作用下斜坡倾倒变形演化路径见图8。

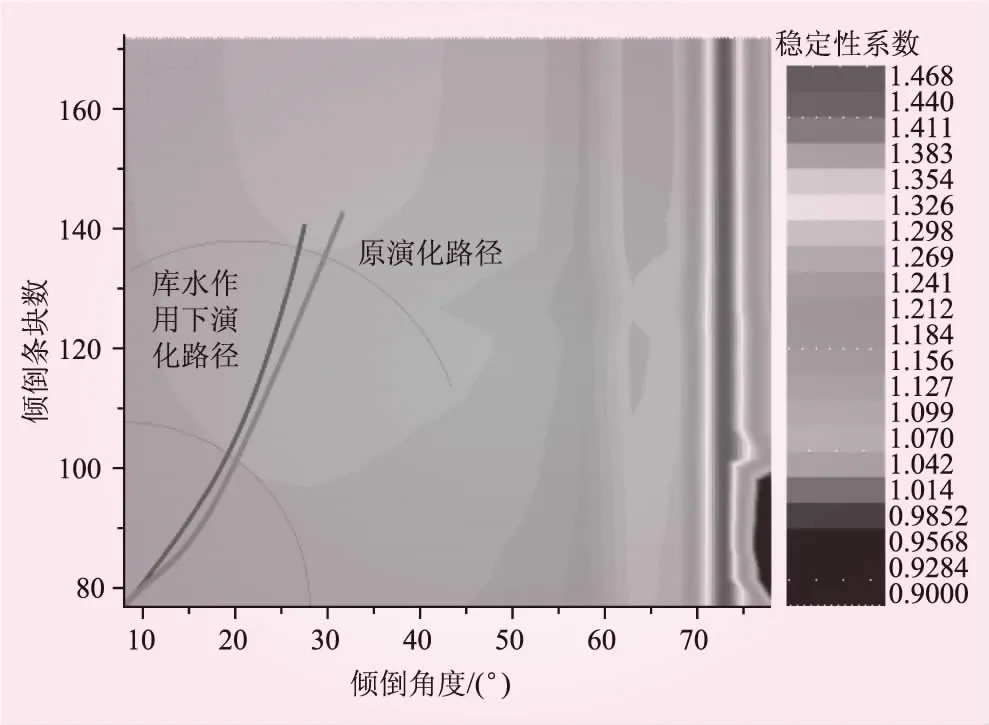
图8 库水作用下斜坡倾倒变形演化路径

从图8可知，库水作用加入后，斜坡稳定性演化路径发生轻微偏移，无显著差异，但斜坡的稳定性降低较明显，平均降低约0.2左右。因此可以推断，库水因素只是降低了反倾斜坡各阶段的稳定性，但对其演化路径影响较小，即只是加速了反倾斜坡的变形。

4 结 语

本文在现场地质调查与各种勘测技术成果的基础上，获取了反倾斜坡稳定性评价剖面，利用Sarma法计算反倾斜坡倾倒变形稳定性系数，并通过稳定性演化路径研究了倾倒变形演化特征，得出以下结论：

(1)反倾斜坡倾倒变形稳定性演化路径拐点位于倾倒条块数80块(约斜坡整体条块数的一半)、倾倒角度8°附近，拐点前后反倾斜坡变形特征差异较明显。

(2)反倾斜坡倾倒变形前期变形方式表现为以倾倒条块数增加为主，条块倾倒倾角增加较缓慢，因此宏观上倾倒变形特征不够明显；进入拐点后，其变形将发生较明显转变，表现为倾倒条块数和倾倒角度同步快速增加，宏观上呈现典型的倾倒变形特征。

(3)库水等外因对反倾斜坡稳定性降低较明显，但对稳定性演化路径的改变较小，表明库水等外因只是加剧了反倾斜坡的变形速率，对其演化方向影响较小。