基于SWAT模型和SUFI-2算法的碧流河流域径流模拟

刘 宁，张 霞，祝雪萍，赵志怀，武鹏林

(太原理工大学水利科学与工程学院，山西太原030024)

碧流河流域水资源是供应城市用水的主要水源，径流则是更直接的水源。研究评价SWAT模型对该流域的径流模拟情况，结合流域水文要素变化以及利用自动率定法率定参数并较准确的预测径流、模拟径流意义重大，将为进一步模拟未来气候情景下的径流奠定基础。

基于物理基础的SWAT模型在研究流域水循环的影响方面作出了积极贡献，可以模拟流域内发生的各种物理过程，被应运于很多方面[1-2]。在非点源污染方面，Li等研究SWAT模型在江西省涟水流域进行多尺度的泥沙模拟研究以及氮和磷的输移过程[3]。在径流模拟方面，姚苏红等[4]以内蒙古闪电河流域为例，应用SWAT模型进行径流模拟，结果显示模拟结果受参数影响很大。张余庆[5]等学者以及宋增芳[6]等学者，均利用SWAT结合SUFI-2分别对修水流域、石羊河流域进行径流模拟，有效控制了参数对模拟结果的影响。曹明亮[7]以碧流河流域为例，利用SWAT模型率定法对多站点进行研究，验证了模型的适用性；但在参数敏感性分析、模拟结果评价以及不确定分析方面使用SWAT模型自带的调参功能进行参数校准，该方法不仅耗时长、分析率定的参数较少、对经验要求高且易受人为因素影响。

故本文将SWAT模型应用于碧流河流域径流模拟。在分析流域水文要素变化的基础上，结合自动率定工具SWAT-CUP，利用其中的SUFI-2算法对参数自动率定、敏感性排序，并对模拟结果分析评价，弥补了SWAT模型自带校准功能的不足，最后多角度分析模拟结果。

1 研究区概况

碧流河属于北温带湿润气候区，6月～9月为汛期，尤其集中在7月～8月多年平均降雨量为742.8 mm，多年平均径流深为294.5 mm，多年多年平均蒸发量为1 404.4 mm，流域面积2 814 km2，坝址以上控制流域面积2 085 km2。1975年兴建的碧流河水库是流域内的主要水库(总库容9.34亿m3)，主要功能为向大连市供水。流域内以林地和耕地为主，以草甸土、棕壤性土为主要土壤类型。2001年建成了控制流域面积为313 km2的玉石水库。

流域内有小石硼、桂云花、天益等9个雨量站，有茧场、碧流河、玉石水库3个水文站。其中，碧流河水文站作为径流模拟站点(见图1)。

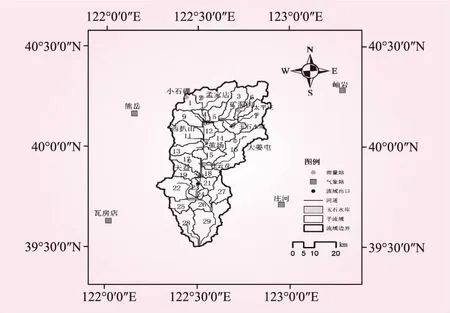
图1 碧流河流域示意

2 研究方法

2.1 SWAT分布式水文模型

SWAT模型是流域尺度的分布式动态水文模型[2]，以水量平衡方程为问题研究的驱动力，综合考虑气候、下垫面等因素，模拟水文过程。该模型的分布式运算特点如下：先根据DEM及实际水网把流域划分为多个子流域；而后对子流域内的水文响应单元进行聚类分析，在此基础上获得不同时间尺度的模拟结果。

2.2 SUFI-2算法

SWAT-CUP中内嵌了5种算法。李倩楠[8]等对5种不确定性评价方法进行了比较，得出SUFI-2方法运算效率高，运行次数少，却能得到较好的结果，故本研究选择此法。

SUFI-2是利用拉丁超立方体抽样法获得参数值带入模型进行模拟[9]。其敏感性分析通过Global以及One-at-a-time敏感性分析实现，其原理可参见SWAT-CUP说明手册。此外，该算法通过P-factor(95%不确定性区间内的观测数据的百分数)和R-factor(95PPU上下限的平均距离与标准偏差的比值)评价参数不确定性程度，P-factor的理论值区间为0～100%、R-factor的理论值区间为0～+∞。当P-factor=1，且R-factor=0时，为完全理想的模拟结果；故通常以P-factor→1，且R-factor→0的程度来判断模拟效果。但P-factor的增大会导致R-factor也增大，因此要找到二者的相对最佳值。

SUFI-2算法：首先，需定义较大的参数范围(结合文献分析以及SUFI-2推荐的参数范围确定)；然后，按照SUFI-2算法运行要求，设定各参数范围、模拟次数及实测值等文件，并选择目标函数；最后，由程序进行多次迭代，依据迭代结果纳西效率系数(Ens)、相关系数(R2)、相对偏差(PBIAS)、P-factor和R-factor的值)调整参数范围，直至获得理想的迭代结果。

2.3 模型的评价标准

前述迭代结果显示的5个指标即为模型的评价指标。其中模型的不确定性评价用：P-factor、R-factor；PBIAS、Ens和R23个指标用于评价模拟精度，计算公式如下：

(1)

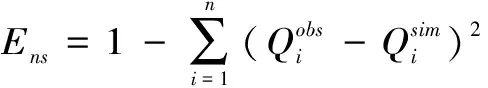
(2)

(3)

当PBIAS<25%，Ens>0.5，R2>0.6时，模型的模拟结果可信；Ens≥0.65时，认为模拟结果很好[10-11]。P-factor>0.5且R-factor<1.5时，模拟不确定性可接受[12]；当P-factor>0.5且P-factor>0.7时，模拟的不确定性较小[13]。

3 碧流河水文要素变化分析

水文要素主要包括降雨、径流、温度、等水文循环相关的时间序列。其中，降雨是径流的直接来源，而径流则是降雨最直观的输出形式。为了通过历史趋势了解水文要素的总体趋势，参照文献[14]给出的1958年～2011年的分析结果，对研究区间1978年～2011年的降水及径流变化趋势进行了分析(见图2)。其分析可得出相似的结论：降雨和径流都为下降趋势，径流的下降趋势更明显。此外，与多年平均径流量对比可知，丰水年在1979年、1985年及1995年出现、枯水年在2002年、2011年出现；同时，1995年之前，偏丰水年多于偏枯水年，而1995年之后偏枯水年多于偏丰水年，同样验证了径流的下降趋势，其下降的原因可能与当下气候全球变暖导致的降水、气温等气象要素有关，有待下一步研究。

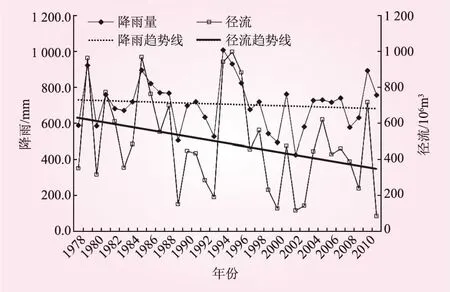
图2 碧流河水库流域1958年～2011年降雨径流系列变化

4 模型数据准备

SWAT模型需要输入的数据和来源如表1所示。气象数据包括相对湿度、温度、风速、太阳辐射等。

表1 模型数据

4.1 空间数据

本文使用的DEM数据为SRTM 90 m精度栅格型数据，2 000 s 1∶10万的土地利用分布图，土壤数据选择1∶100万数字化土壤图件。将各空间数据投影类型统一转换为WGS_1984_UTM_ZONE_51N，并对应于SWAT模型的代码，重新分类(见表2、3)。

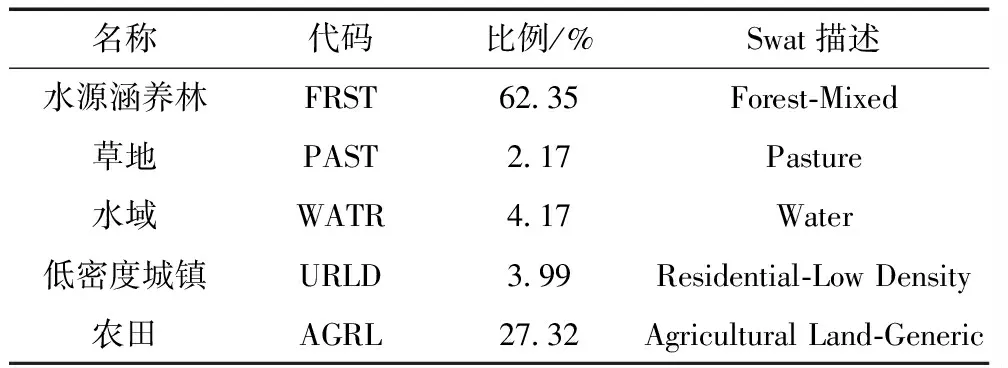
表2 碧流河水库上游土地利用类型重分类结果

表3 碧流河水库上游土壤类型

4.2 属性数据

属性数据的处理有：土壤属性数据库的建立和天气发生器相关参数的计算。

由于土壤分类系统记录的土壤属性的参数与SWAT模型输入要求的土壤属性标准不同，在建立土壤属性数据库前要将国际制标准转换为美制标准。对土壤水特性参数的获得方式为：借助软件SPAW以及直接应用。

SWAT模型天气发生器的参数计算由于工作量较大，运用计算程序SwatWeather.exe(北京师范大学建)进行，将气象数据整理后导入程序，得到模型需要的数据[15]。

5 结果分析

对碧流河水库流域构建SWAT模型，流域共划分为29个子流域，碧流河水文站位于第21号子流域，限于当前碧流河水文站缺乏日径流数据，对该水文站进行月模拟后输出结果，并进一步在SWAT-CUP中按算法要求建立SUFI-2工程、输入相应的要求文件得到模拟评价结果，进而评价分析。

5.1 参数率定及敏感性分析

SWAT模型能够相对准确地模拟径流的关键在于将众多的SWAT模型中与径流有关的参数选出，去除对模拟结果影响较小的参数，进行敏感性分析、率定。本文通过前述SWAT-CUP的敏感性分析方法最终选出14个最为敏感的参数校准，部分参数含义具体如下：CN2为平均湿度时的SCS曲线数，值越大，径流总量越大；SOL_AWC为田间持水量越大，可下渗水量越少，渗透时间越短；GW_DELAY用于计算每天流入地下水层的回灌水量，与水平面的深度和渗漏区及地下水区地质组成的水力特性有关；GW_REVAP值越大，再蒸发量越多，当等于1时，蒸发量等于潜蒸发量；CH_K2：默认为0，值越大，河道输移损失越大；REVAPMN：只有当浅层地下水层的含水量超过阈值aqshthr，rvp时，再蒸发过程才发生。CH_N2：值越大，汇流流速越小；RCHRG_DP值越大，回灌水流入深层地下水层的比例越大；SOL_K为值越大，由土壤层流入下一土壤层的水量就越多，同时产生的壤中流也越多。

表4 参数敏感性及参数率定分析结果

注：①R、V为两种修改参数的方法，分别是乘以某值(百分百浮动)、赋值；②t-stat越大表示参数越敏感，p-value值表示t值的显著程度，越接近0值越显著。

按照相应的修改方案设定参数初始范围，经过多次迭代(每次迭代次数设置为200次)逐步满足评价指标，得到参数敏感性分析以及率定结果如图3及表4所示。

图3 参数敏感性分析(P-Value及t-stat)结果

图3及表4呈现率定后参数的最终范围、最佳值及敏感性判定原则，排在第一位敏感的参数为：CN2，其P值最大，t检验值最小，同样的判断原理，接下来依次为：SOL_AWS、GW_REVAP、GW_REVAP、GWQMN等，其对模拟结果影响逐渐减小。

5.2 模型模拟结果的分析和评价

按照碧流河降雨和径流变化趋势分析结果，将1978年～2011年模拟期的前两年作为预热期，1981年～1995年作为率定期，1996年～2011年作为模型的验证期，建立模型并获得模拟结果。利用前述3个评价指标对模拟结果进行评价。模型在不同时期的月值模拟结果如图4、5所示，评价指标见表5。

模拟结果显示：①碧流河水文站的模拟值与观测值变化趋势一致性良好、流量过程拟合良好，率定期、验证期R2分别为0.92、0.91；Ens分别为0.91、0.90；PBIAS分别均控制在5%以内，且全部落在较小的不确定区间内(95PPU)。②但对峰值的模拟效果较差，模拟值普遍小于实测值，可能由于未考虑融雪影响而致。③验证期(1995年～2011年)的模拟效果略低于率定期(1980年～1995年)的模拟效果，可能与SWAT模型对丰、枯水年的模拟精度不同有关，偏枯水年模拟精度低于偏丰水年模拟精度[16]。

再从碧流河月径流分布来分析，如图6给出了两个时段(1981年～1995年、1996年～2011年)多年平均月径流变化，6月～9月是碧流河丰水期，8月达到径流峰值，之后开始下降，10月至次年5月为枯水期，丰枯时段区分明显，这与碧流河年内降水时间分布有关。一年降水峰值主要集中在主汛期(7月～8月附近)，图中同样可见模型对峰值模拟效果较差。

图4 月径流率定期模拟结果(1981年～1995年)

图5 月径流验证期模拟结果(1996年～2011年)

时期P-factorR-factorR2EnsPBIAS/%率定期0.880.610.920.91-3.80验证期0.910.610.910.901.30

图6 观测和模拟的多年平均月径流变化

5.3 模型不确定性分析

水文过程包含着各种不确定性因素。对于水文模型，通常是运用大量的概化或经验公式对实际流域的水文循环过程的一个简化，各方面的不确定性往往相互作用而影响模型输出结果的不确定性。

本文不确定性结果显示，率定期P-factor为0.88、R-factor为0.61，依据判别条件，满足P-factor>0.7、R-factor<1不确定性较小的条件，模型模拟结果较适用。验证期与率定期基本一致，而略高的P-factor表明：90%的观测值落在95%置信水平的不确定性区间内，模拟的不确定性相对更小。但从图4、5可看出，丰水期模拟的不确定性区间依然较大，而峰值模拟的不确定性更大。

6 结 语

SWAT模型在碧流河流域的径流模拟中在前人手动率定较少参数的基础上，延长模拟时期，利用自动率定SUFI-2算法提升了模拟效果，并验证了相对较小的不确定性，为下一步的气候模式与SWAT模型耦合筑牢了基础；同时也发现，该模型对碧流河的峰值模拟效果不佳、不确定性只是综合考虑，应在后续的研究中深入综合考虑更多气候变化与人类活动等因素。另外限于水文资料的限制，仅利用一个碧流河水文站序列进行分析，代表性方面有一定欠缺，需要进一步获取更多水文站数据深入研究；此外，敏感性分析得到的14个参数其各参数对结果的影响贡献率多大，有待继续探讨。