基于带有噪声输入的稀疏高斯过程的人体姿态估计
2019-06-22夏嘉欣陈曦林金星李伟鹏吴奇
夏嘉欣 陈曦 林金星 李伟鹏 吴奇
人体姿态估计是利用图像特征来估计各个人体部位在图像中的具体位置的研究过程[1],是一种应用广泛的结构化预测问题.由于人体姿态估计在视觉跟踪、计算机动画[2]以及智能监控、虚拟现实[3]等领域均有广泛的应用,因此,在过去几十年中,关于人体姿态估计问题的解决方法层出不穷.
高斯过程(Gaussian process,GP)[2−5]及其变体[6]是一种典型且有效的人体姿态估计方法.作为一种常见的基于贝叶斯概率论进行预测的回归方法,高斯过程因其对非线性、高维、复杂和小样本问题的灵活性、有效性[4]及泛化能力强,被广泛应用于各个领域.然而,人体姿态估计本身通常需要较大的样本集,所以简单地将高斯过程的基本模型应用于此类问题会耗费大量的运行时间与运算空间.同时,由于高斯模型本身对于噪声影响缺乏较高的鲁棒性,而人体姿态估计等高维预测问题在实际应用中本身就将受到大量的噪声干扰,传统高斯模型的预测准确性也将受到影响.因此,对于大样本问题预测的计算复杂度和对于噪声输入的预测准确性,成为制约高斯过程应用于人体姿态估计问题的重要因素.但是,人体姿态估计作为一种非线性多元输入输出的拟合问题,由于其输入输出变量的高维性,该问题的预测模型本身就需要解决模型较为复杂、模型参数较多、超参数难以确定等种种问题.而与当前更为主流的预测算法相比,高斯过程具有模型容易实现,参数复杂性低,超参数自适应获取,无需海量训练数据,以及输出具有物理意义等突出优点,这些优点注定了高斯过程在解决非线性高维预测问题方面的巨大优势与潜力.因此,若能同时改善计算复杂度与噪声鲁棒性这两项缺陷,那么高斯过程将在解决人体姿势估计,乃至所有多元输入输出问题方面,发挥更加重要的作用,产生更加深远的影响.
基于上述原因,计算复杂度是高斯过程应用于人类姿态估计的一个重要的考虑因素.稀疏高斯过程、混合专家模型[7−8]、增量式学习[9−10]方法等均是有效降低高斯过程计算复杂度的方法.其中,稀疏高斯过程最为常用.该方法的本质为使用一组诱发输入(Inducing input)部分替代原输入进行假设[11]与训练.应用常规的高斯过程回归(Gaussian process regression,GPR)需要O(n2)的存储空间和O(n3)的运行时间,其中n是训练点的数量.由于人体姿态模型包含了数以千计的高维数据点,因此其计算复杂度超乎想象.然而,如果运用稀疏高斯过程解决问题,则存储空间将减少到O(nm),而运行时间则将减少到O(nm2),其中m是诱发输入点的个数.由于m¿n,空间和时间成本得以显著降低.本文将采用稀疏算法中的一种较为优秀的算法:完全独立训练条件(Fully independent training conditional,FITC)[12]法,来降低人类姿态估计问题中高斯回归的计算复杂度.
输入输出噪声是高斯算法的另一个重要考虑因素.对于高斯回归的噪声研究始于很早之前,但在大约十年前,噪声才被扩展到应用于解决大规模和高维输入输出[13]的问题.对于测试输入样本的噪声,可通过矩匹配的方法进行解决,而对于训练输入样本的噪声,先前的方法具有较高的计算复杂度.为了解决这一问题,McHutchon等[14]在2011年提出了一种全新的算法,本文将应用该方法来处理人体姿态估计问题中的输入噪声.
早在1975年,人体关节模型就已经被证明包含有丰富的信息,并可用于行为识别.此后的几十年,众多研究人员均致力于三维人类姿态的重建[15−16]与信息提取[17−19],几乎所有的经典模型如高斯过程、支持向量机、人工神经网络等,都已经被成功且成熟地应用于人体姿态估计问题.因此,在近几年有关该问题的研究中,更多的人着眼于通过提出更加新颖而复杂预测模型来提高人体姿态估计的预测精度[3,20−21],或通过在现有算法中加入新的优化模型形成混合模型来提升算法性能[1,22],但着眼于从单个已成熟模型本身的数学机理出发,通过改进其数学模型来提高人体姿态估计算法性能的研究则少之又少.模型的数学原理是预测模型的根基,从经典模型的数学原理角度对模型进行优化,不但保证了模型的稳定性与可推广性,还可以达到比参数优化更好更彻底的优化效果.因此,本文从高斯过程本身的数学原理出发,利用稀疏算法与带有噪声输入的算法这两种优化方法进行模型改进,并将改进后的模型应用于三维人体姿态估计问题,在降低计算复杂性的同时,也使得算法在输入噪声的影响下获得更好的预测精度.相较于现有算法而言,本文算法具有更强大的数学基础与泛化能力,可以推广应用于多种结构化预测问题.
本文结构安排如下:第1节对人体姿态估计问题进行描述;第2节介绍了高斯过程的模型,包括标准高斯过程;第3节介绍带噪声输入的稀疏高斯算法,同时对该算法的合理性和优越性进行简单验证.第4节将本文算法与其他预测效果较好的人体姿态估计算法应用于HoG样本集[17],并对预测结果进行比较与评估.第5节为结论.
1 问题描述
人体姿态估计是人体动作与行为的识别与分析的一个基础问题[22].由于其在人机交互[23]、人体活动分析和视频监控等领域都有着广泛的应用前景[20],因此关于人体姿态估计的方法也层出不穷.在现有的人体姿态估计的算法中,基于模型的方法更被研究者关注.该方法的主要思路是通过建立数学模型来描述人体特征与空间位置,并度量人体部位可能定位区域与真实人体部位外观的相似程度,从而获得标准的输入输出集,然后设计推理算法来确定相似度较高且符合人体模型约束的各部位定位区域[1].
在实际问题中,实验个体所处环境往往比较复杂,会很大程度上增加外观模型的建立难度,因此,选取适当且有效的图像特征来简化模型建立过程十分重要.本文考虑选取比较典型的方向梯度直方图特征(Histogram of oriented gradients,HoG).HoG特征计算的主要过程为:1)计算图像每个像素的梯度大小和方向,划分图像;2)将若干像素组成一个单元(Cell),统计每个单元的梯度直方图,形成每个单元的特征描述;3)将若干单元组成一个块(Block),将每个块内所有单元的特征描述串联,得到每个块的HoG特征描述;4)将图像内的所有块的HoG特征描述串联,得到整个图像的HoG特征.HoG不是考察图像的单个像素的特征,而是通过计算局部区域中的定向梯度直方图以形成图像特征,因此对光线和小幅度的位置偏移并不敏感.
由于HoG特征在人体姿态估计领域具有十分优秀的特征描述能力,近年来使用HOG特征实现人体检测与估计系统成为研究热点[24].本文的研究重点在于预测算法的提出与优化,而非特征模型的建立,因此,本文借用Poppe[17]基于Sigal等提出的HumanEva-I[16]数据库建立的人体姿态HoG特征样本集进行仿真实验与分析.
HumanEva-I是一个由视频序列组成的数据库,该数据库中的视频序列由3个不同视角下的摄相机获取,包含4名受试者的6种常见的行为.
在本文算法中,定义输入变量X=(x1, X2,···,xN)T,输出变量Y=(y1,y2,···,yN)T,输入输出均为高维变量,其中,N为样本个数,X为D维向量,y为E维向量.HoG特征输入样本集X的建立过程如下:以单个摄相机获取的单帧图片为例,1)将图片进行背景删除、二值化、提取兴趣区域(Region of interest,ROI)等预处理操作;2)将ROI区域划分为5行6列的30个网格,每个网格统计出9个HoG特征,并将30个网格的HoG特征串联,得到单一视角下的270维HoG特征;3)将3个视角下的特征串联,形成810维HoG特征描述,该特征即为输入集X下的单个样本x.输出变量样本集Y下的单个样本y是由20个三维身体关节位置坐标组合成的60维向量,代表在x描述下的人体姿态模型.
2 高斯过程模型
2.1 高斯过程标准模型
高斯过程是一种基于贝叶斯线性回归产生的一种回归模型.与其他常用的预测算法相比,高斯过程具有容易实现,超参数自适应获取等优点.
回归过程,简单来说就是根据训练集Xm与Ym之间的映射关系,预测新的测试点X∗最有可能的对应输出值Y∗的过程.高斯回归是在贝叶斯线性回归的基础上,把自变量空间通过核函数映射到高维空间,从而得到更好的预测结果的过程.
在高斯过程回归中,时间域上所有随机变量均服从高斯联合分布,其性质完全由均值函数和协方差函数确定.在实际观测中,观测值可能会受到噪声污染,假设噪声变量服从,输出样本集Y的先验分布可以表示为
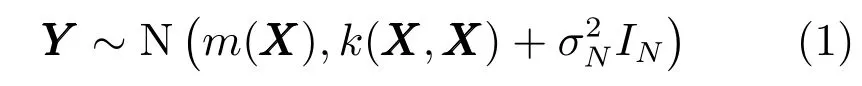
因此,已知的训练输出值Ym与未知的测试输出值Y∗的关系可以表示为
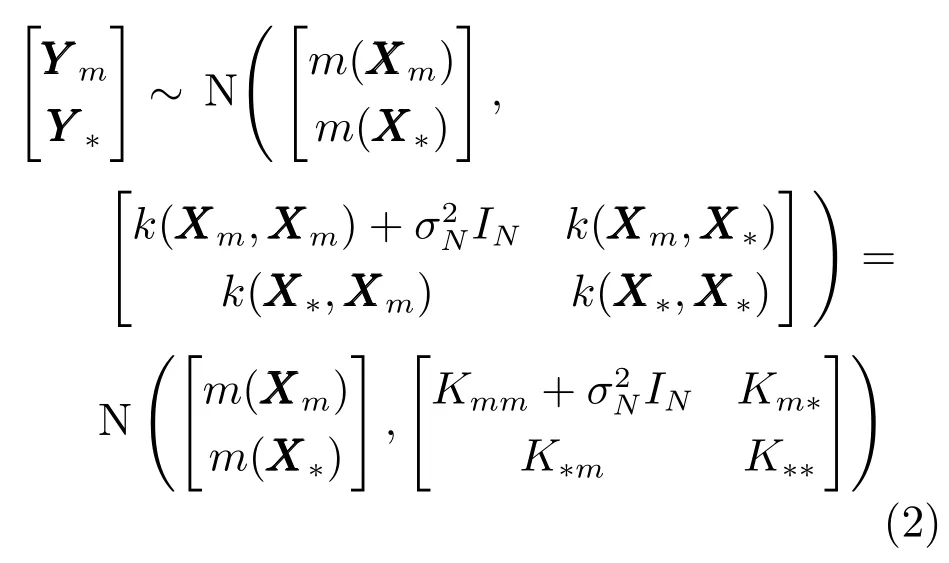
其中,Xm表示训练输入值,X∗表示测试输入值,m(X)表示X的均值函数,k(X,X')表示X与X'协方差函数,K∗∗,K∗m,Km∗,Kmm分别是K(X∗,X∗),K(X∗,Xm),K(Xm,X∗),K(Xm,Xm)的简写形式.
由于变量Ym已知,因此由贝叶斯公式可知,后验传递函数p(Y∗|Ym)为
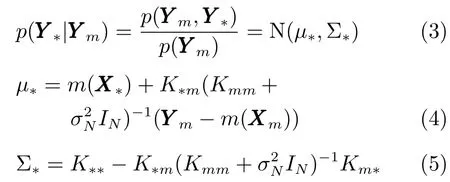
其中,p(Ym,Y∗)为先验传递函数,p(Y∗|Ym)为高斯函数.
由式(3)~(5)可知,由于时间域上所有随机变量均服从联合高斯分布,因此该高斯过程可以被均值函数m(X)和协方差函数k(X,X')共同唯一决定.同时,k(X,X')被称为从低维空间到高维空间映射的核函数.在高斯过程中,常用的核函数有常数核(Constant function)、线性核(Linear function)、径向基核(Radial basis function)等,本文采用的协方差函数为平方指数协方差函数(Squared exponential correlation function),即

1)建立训练样本条件概率的负对数似然函数及其关于θ的偏导数.

其中,Ym为训练样本集,Kmm为训练样本协方差函数,N为训练样本数,i为超参数集的第i个元素.
2)采用梯度下降法对偏导数进行优化,通过规定的迭代次数,得到超参数的最优解.
2.2 稀疏高斯过程
稀疏高斯过程是通过选取一定数目的诱发输入点来部分代替原输入点进行训练,从而降低运算复杂度的方法.
在本文实验中,由于输出变量yi(1≤i≤N)彼此之间相互独立,符合完全独立训练条件(FITC),因此,在各种变量假设均与前文相同的基础上,同时假设Y变量彼此之间相互独立,即

其中,,且与Yu是诱发输入与输出.该条件即为完全独立条件.在该条件下,先验传递函数可表示为

其中,对于每个1≤i≤N而言,,.
在此处,定义Qac为

其中,


证明.首先,考虑c在给定的xb下的条件分布函数.以xa为例:

由于均值向量与协方差矩阵均已知,因此可以得到xa与Xb的联合概率分布.同时,通过积分求得边缘分布.因此,变量Xa在给定的xb下的条件概率的协方差为
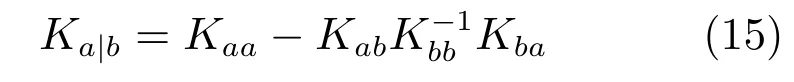
同理,变量Xc在给定的xb下的条件概率的协方差为

求Xa与xc在Xb条件下的联合概率分布,可得其协方差矩阵为

因为xa与xc关于给定的Xb条件独立,所以,即,.
□
通过上述证明过程,可以将式(10)改写为

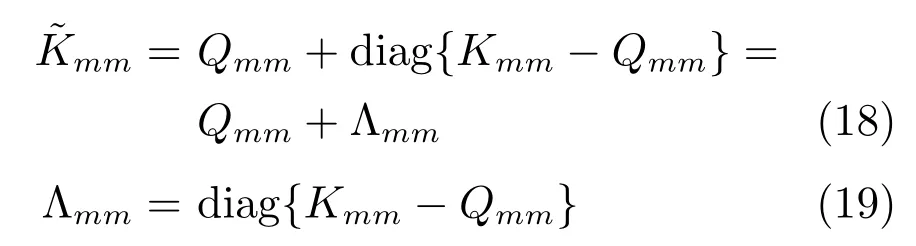
则Yu的后验传递函数可以表示为
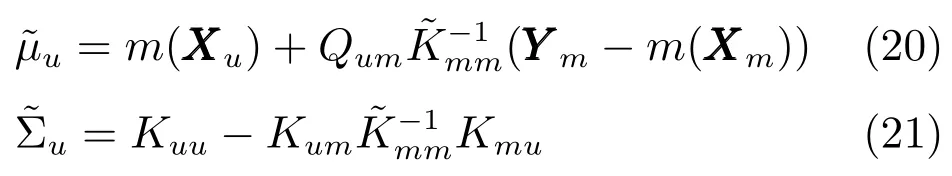
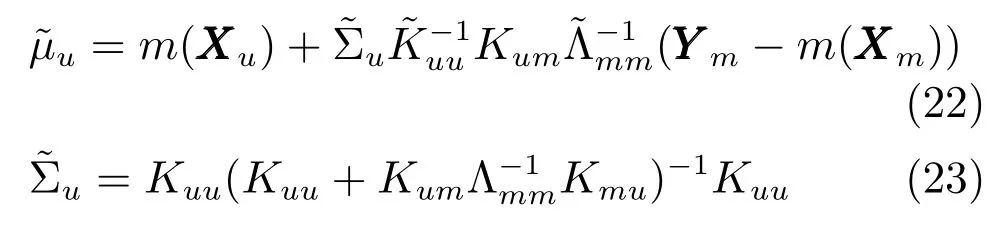
所以,Y∗的后验传递函数为

从上述等式可以看出,我们需要计算一个n×n的矩阵Λmm与几个m×m矩阵的逆矩阵.由于m¿n,并且Λmm为对角阵,因此算法的计算复杂度得到了明显的改善.
如果假设输入变量X服从零期望值的高斯分布,则其后验分布函数可以表示为

2.3 带有噪声输入的高斯过程
在标准的高斯过程中,常常存在两个假设:其一是训练和用于测试的输入值Xm和X∗均为无噪声的;其二是观测输出值Ym受到一个均值为零,协方差为常数的高斯噪声ε的干扰.但是在实际测量中,Xm和X∗却并非是无噪声的.也就是说,输入值X并非某个确定的值,而是一个随机变量.
2.3.1 测试输入点为随机变量
由前文可知,当测试输入点X∗为确定值时,后验传递函数p(Y∗|Ym)表达式如式(3)~(5)所示.
但现在假设X∗并非确定值,而是一个服从高斯分布的随机变量,即
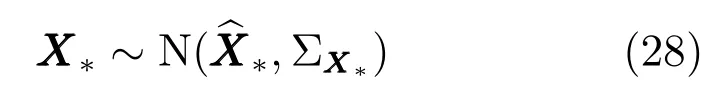
若在此条件下得到Y∗的后验分布,最直观的方法是运用边缘概率密度与积分进行计算.但是,在这一过程中,不但需要计算带有逆矩阵的指数的积分,同时以上计算过程的结果还由一个非线性的随机变量X∗决定,因此计算过程太过复杂,无法直接计算出积分结果.
为了解决积分计算过于复杂的问题,本文采用矩匹配(Moment matching)的方法,规定p(Y∗)服从高斯分布,通过求取其均值与方差来确定预测点Y∗的值.
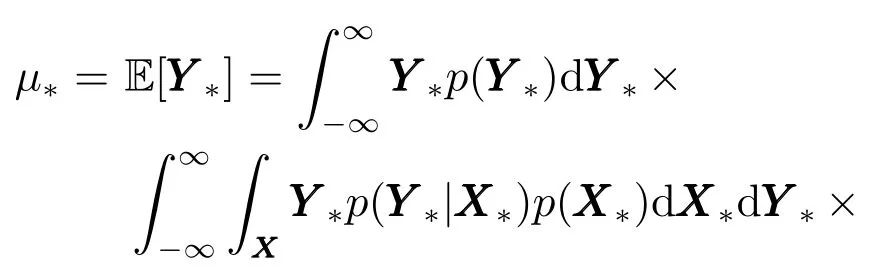
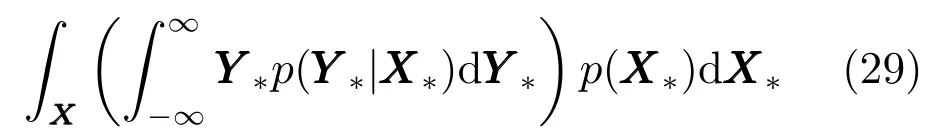

为简化上式,定义

则式(30)可以改写为

若假设m(X)=0,且协方差函数K为式(6)形式的平方指数协方差函数,则可以表示为

观察上式可以发现,若X∗为确定值,即且,则,此时式 (31)与式(4)相等.
2.3.2 训练输入点为随机变量
同第2.3.1节,假设Xm并非确定值,而是一个服从高斯分布的随机变量,即

若在此条件下运用边缘概率密度与积分计算Y∗的后验分布,则会遇到与第2.3.1节相同的问题,计算过程太过复杂,无法直接计算出积分结果.假如将第2.3.1节中的矩匹配方法应用于此处,可以得到

为了解决训练集的噪声输入问题,采用一种全新的方法进行计算,该算法称为带有噪声输入的高斯过程(Noisy input Gaussian process,NIGP),主要思想是将训练集的输入噪声转化为输出噪声,运用常规的高斯过程回归解决问题.
首先做如下假设:对于输入样本集Xm与输出样本集Ym,假设其中的单个样本x与y分别为真值在噪声影响下的测量值,由此可得
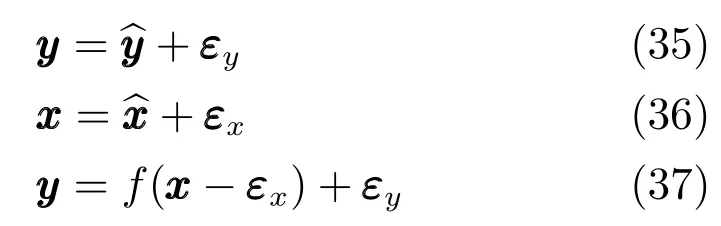
其中,εy~N(0,Σy),εx~N(0,Σx). 不难看出,式(35)与式(1)假设的条件相同,式(36)扩大到整个样本集即为式(33).
随后,将f(X−εx) 在x附近进行Taylor展开,并只取到一阶导数,即可得到关于噪声的一阶模型:
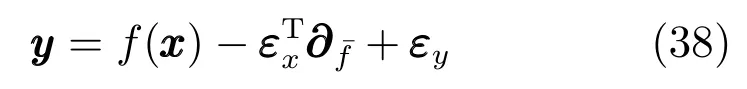

将式(39)与先验传递函数进行联立,并且扩展到整个样本集,由此得到后验函数的均值和协方差为
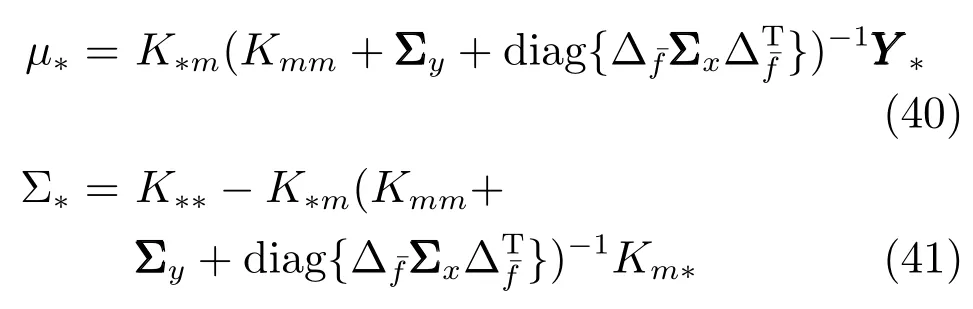
3 带有噪声输入的稀疏高斯过程
本文第2.2节介绍了稀疏高斯过程,第2.3节介绍了带有噪声输入的高斯过程.两种算法均具有不同的原理与推导过程,本节要在验证其合理性的基础上,将两种算法进行结合,得到更为广泛的适用范围及更好的预测结果.
3.1 建议模型
由第2.3节的推导过程可知,在稀疏高斯过程中,Y∗的后验分布的均值与协方差如式(24)和式(25)所示.通过观察可以发现,式(24)与式(4)的表达形式相同,由此可以推断式(24)可直接运用式(4)的运算过程.论证如下:
根据矩匹配算法原理,将式(24)代入式(30),得
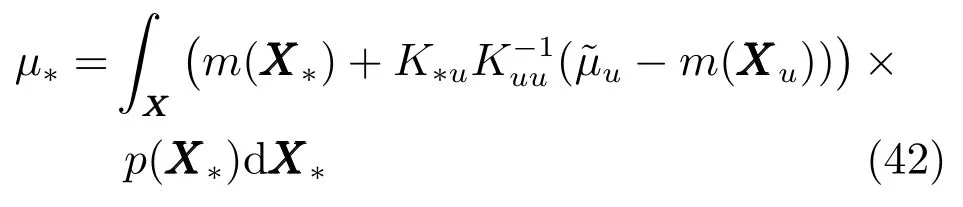

对于训练样本集Xm在噪声影响下的结果应用于稀疏高斯过程,原理与测试样本在噪声影响下的原理相同.因此,可由式(40)和式(42),得到带有噪声输入的稀疏高斯过程(Sparse Gaussian process with input noise,SGPIN)的预测输出值Y∗的后验分布的均值.
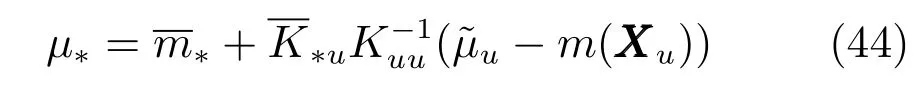
其中,

如果假设输入变量X服从零期望值的高斯分布,则µ∗可以改写为

其中,

而对于Y∗的后验分布的方差,由于其推导过程过于复杂且占用较大篇幅,同时对预测结果没有实质性影响,因此只列出推导结果:

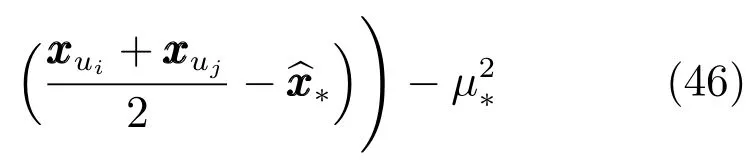
其中,

3.2 样例测试
本文将稀疏高斯过程和有噪声输入的高斯模型相融合,提出了一种全新的SGPIN算法.在将该算法应用于人体姿态估计问题之前,为了进一步验证该种融合的必要性与合理性,采用一些简单的数据对SGPIN算法、稀疏高斯算法(FITC)、有噪声输入的高斯算法(NIGP)和常规高斯算法(GP)进行测试与评估.
如图1所示,在定义域为[−5,5]、值域为[0,2.5]内随机生成一条输入输出曲线,并将该曲线设定为待预测的理想目标曲线.在曲线上均匀选取若干个点,并人为添加高斯噪声,组成带有噪声输入的训练集.随后分别运用GP,FITC,NIGP和SGPIN四种算法进行预测,得到预测曲线,同时对每种算法的均方误差(Mean squared error,MSE)和预测时间进行比较与评估,评估结果(10次重复实验取平均值)如表1所示.
结合图1与表1中的信息可知,SGPIN算法在预测准确度与运行时间方面均明显优于其他三种基础算法,可见稀疏算法与去噪算法的结合确实可以大幅度提高高斯过程算法的性能,达到更好更彻底的优化效果.

图1 GP,FITC,NIGP和SGPIN算法预测结果Fig.1 Predicting results of GP,FITC,NIGP and SGPIN

表1 GP,FITC,NIGP和SGPIN算法比较Table 1 Comparison of GP,FITC,NIGP and SGPIN
4 仿真研究与结果分析
本节主要对带有噪声输入的稀疏高斯(SGPIN)算法与双高斯过程算法(Twin Gaussian processes,TGP)、K–近邻算法(K-nearest neighbor,KNN)等预测算法进行比较与评估.其中,TGP算法是由Bo等[25]提出的一种基于输入与输入两种联合概率分布的高斯过程,在解决人体姿态估计问题时,具有比K–近邻算法、岭回归算法以及传统高斯过程等算法更高的预测准确度.
实验的数据集来自基于HumanEva-I数据库[16]的人体姿态HoG特征集[17],包括3位测试对象的行走、慢跑、投掷捕捉,做手势与拳击5个动作.更多细节可以参考文献[17].
4.1 输入、输出与误差度量
1)表2为实验的数据集,包含不用姿势和不同研究对象的样本个数(每个视角下的单帧图片数).对每个样本使用由Poppe计算的810维HoG特征描述[17],同时,这个数据也用于评估双高斯过程和KNN等算法的性能[25].
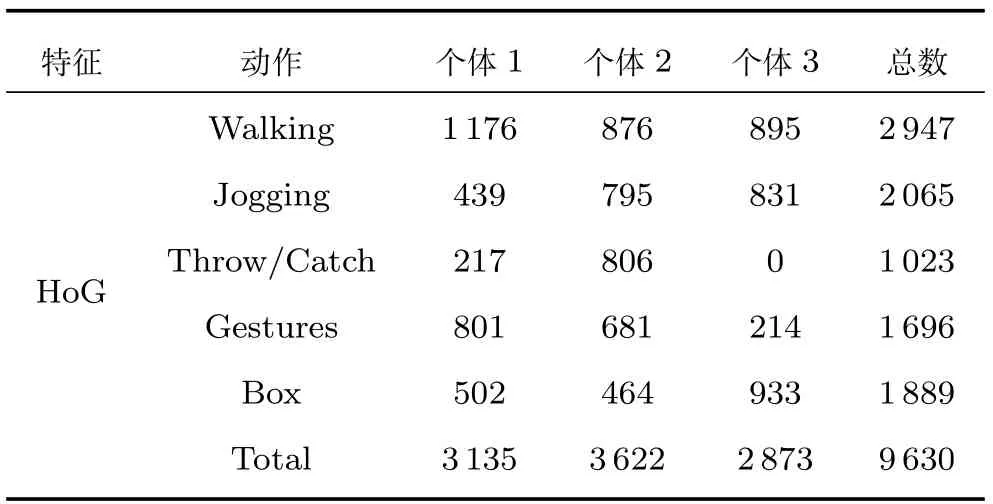
表2 实验数据集Table 2 Experimental set
2)输出变量是人体姿态,表示为20个三维身体关节位置组合成的60维向量,并且每个姿势都需要进行预处理,即将根关节位置设为原点,其他关节的位置表示为与根关节的位置差.这种标准化处理可以减少因研究对象的不同产生的不确定性.
3)借用文献[16]提出的误差度量,对于每一个输出向量,误差公式可以表示为
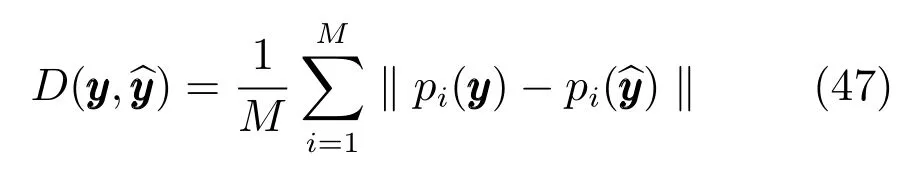
其中,y是60维的估计输出,是与之对应的真实输出,M=20是每一个姿态中关节位置的个数,pi的输出值是第i个关节位置的三维向量.k·k表示欧氏距离.而对于整个输出序列,平均误差可以表示为

其中,N表示输出向量的个数.
4.2 初始化与评估
1)对于每一个数据集,将其分成测试、诱发和训练三部分.在SGPIN算法中,通过迭代的梯度下降法确定超参数值,这种方法会适当增加运行时间,但是却可以得到更好的精度.对于其他算法,忽略诱发部分数据,参考文献[25]进行参数值设定.另外,对于每种算法,都会人为地在测试输入中添加高斯噪声,同时添加一个极小的噪声矩阵来增加逆矩阵运算的稳定性.
2)选取高斯过程(GP)、双高斯过程(TGP)、带有噪声输入的稀疏高斯过程(SGPIN)、带有KNN算法的双高斯过程(TGPKNN)、最优双核复合分类算法(Kernel target alignment,KTA)[26]和希尔伯特施密特的独立性准则(Hilbert-Schmidt independence criterion,HSIC)[27]下的KNN算法进行预测准确度和运行时间的评估.在准确度方面,比较每一个姿势的每一个输出向量的估计误差和不同姿势的平均估计误差.同时,为了保证评估的客观性,每种算法都进行5次仿真运算,取其平均值作为最终的运算结果.
表3列出了不同姿势的平均误差,表4是每一种算法的运行时间.这两个指标是评价算法综合能力的重要依据.
在表3和表4中,所有模型均来自于3个研究对象的5个动作.表中列出了样品数量,最小误差和最短运行时间用粗体字显示,“/”表示无数据集进行评估或样本集过小致使KNN算法无法在与其他样本相同K值下运行,所有模型的诱发点个数均为nu=20.

表3 基于HumanEva-I数据集HoG特征的不同算法的平均误差Table 3 Evaluation of average error of different algorithms based on HoG feature of HumanEva-I

表4 基于HumanEva-I数据集HoG特征的不同算法的运行时间Table 4 Evaluation of runtime of different algorithms based on HoG feature of HumanEva-I
从表3可以看出所有算法的准确性.其中,SGPIN算法最为准确,因为其具有比其他模型更小的平均误差.TGP和TGPKNN的误差在所有的运动中都是相似的,因为这两种方法具有相同的核心算法.KTA和HSICKNN算法与TGP算法的表现比较相似,但KTA算法的预测准确性略优于HSICKNN算法.常规GP模型与其他模型相比具有较大的误差,因为它更受输入噪声的影响与干扰.
同时,从表3可以看出,在预测不同的姿态时,SGPIN算法的优越性不尽相同.在预测Throw/Catch和Gestures等变化比较强烈的姿态时,SGPIN算法的预测准确度格外高,在预测Walking和Jogging这类变化比较平缓的姿态时,则表现了与其他算法相近的预测精度.SGPIN算法的这种表现将在之后的算法稳定性分析中具体讨论.
表4的数据反映了所有算法的运行时间.常规GP算法因为其模型的简单性,比其他算法具有更少的运行时间.另外5种算法在运行时间上没有较大的差别,属于同一数量级.观察表4中的每一列,可以分析出样本数量对运行时间的影响.具体表现为:样品数量对TGP,TGPKNN,KTA以及HSICKNN算法具有很大的影响,对GP的影响较小.在大多数情况下,样本数越小,平均误差也越小.但是,SGPIN算法几乎不受样本大小的影响,因为在SGPIN算法中,承担了主要运算量的诱发点数量不随样本数的变化而变化,其取值均为20.
接下来讨论SGPIN算法的稳定性.图2和图3列举了在同一姿态中每一个输出向量的误差.由于样本数量过大,且预测误差在各样本子集的分布基本相同,因此只截取每个样本集的100个样本进行描述.图2给出了SGPIN算法与TGP和TGPKNN算法的对比结果,图3给出了SGPIN算法与GP,KTA和HSICKNN算法的对比结果.
从图2可以看出,在很多样本中,TGP和TGPKNN的预测误差会随输出向量的不同产生很大的变化,而SGPIN受到的影响较小.此外,若调细图2中的曲线,可以发现TGP曲线存在大量毛刺,而TGPKNN和SGPIN的曲线则更为平滑.原因是TGP算法利用了所有输入点的信息,而TGPKNN和SGPIN算法为了简化计算过程而忽略了一部分输入点.
从图3可以看出,GP几乎不随输出向量的不同而产生变化,原因是GP算法的原理比较简单,注重的是整个样本集的总体信息.SGPIN算法因为稀疏过程的存在,输出向量对测量误差的影响也较小.而KTA和HSICKNN算法与SGPIN算法相比则极不稳定,预测准确度会随样本的不同产生巨大的波动,而预测误差的离散程度也会随样本集的不同而有所不同.

图2 TGP,TGPKNN与SGPIN算法的误差比较Fig.2 Error comparison of TGP,TGPKNN and SGPIN
结合图2和图3可以发现,在预测Walking和Jogging这类变化比较平缓的姿态时,SGPIN算法的稳定性与TGP和TGPKNN算法基本相同,且都弱于GP算法,具体表现为预测曲线的波动程度相似.在预测Throw/Catch和Gestures等变化比较强烈的姿态时,TGP,TGPKNN,KTA和HSICKNN算法的不稳定性使得算法产生了许多预测误差较大的样本,极大影响预测精度,这也是表3中SGPIN算法在预测变化比较强烈的姿态时准确度远远超过其他算法的原因.
另外,在预测同一实验个体的同一种姿态时,预测误差值的离散程度也反映了算法的稳定性.由于在行走姿态的预测中SGPIN算法与其他算法的预测结果最为相似,因此选取个体3的行走姿态,重复进行5次仿真运算,结果如表5所示.

图3 GP,KTA,HSICKNN与SGPIN算法的误差比较Fig.3 Error comparison of GP,KTA,HSICKNN and SGPIN

表5 个体3行走姿态的预测误差Table 5 Predicting errors of subject 3 walking
表5最后一行的方差反映了预测误差值的离散程度.方差越大,算法的稳定性越低,方差越小,算法的稳定性越高.
结合图2、图3和表5可以分析出6种算法的稳定性.HSICKNN和KTA算法极不稳定,TGP和TGPKNN算法稳定性一般,GP算法和SGPIN算法稳定性最好.其中,SGPIN算法无论在预测变化较大的姿态方面,还是在重复运行同一样本集时,都能达到十分稳定的预测精度,这两种性质也充分反映了SGPIN算法是一种能够推广到实际工程应用领域的人体姿态估计算法.
5 结束语
本文提出了一种从经典高斯过程模型的数学原理角度对模型进行优化来解决人体姿态估计问题的新思路.算法的评估实验是基于HumanEva-I数据库的HoG特征集的三维人体姿态估计问题,包括3个研究对象与5个人体姿态.将本文算法与GP算法、TGP算法、TGPKNN算法、HSICKNN算法和KTA算法在预测准确度、运行时间和算法稳定性方面进行比较,本文算法具有较为优秀的评估结果.在算法准确度方面,SGPIN算法与其他算法相比,具有较低的平均误差和较高的稳定性(较小的误差方差和较平滑的误差曲线),TGP和TGPKNN算法在稳定性方面表现一般,KTA算法和HSICKNN算法表现较差.在运行时间方面,SGPIN算法并没有过于优异,但是与其他算法相比其结果依旧是可以接受的.同时考虑预测准确度、算法稳定性与运行时间三项因素,SGPIN算法是一种应用于人体姿态估计问题的更为有效的算法.
未来的工作首先是对于求解超参数的梯度下降算法的改进,因为运用此种方法得到参数需要较长的运行时间,且并未对输入信息进行充分利用.此外,需要更好地利用输入变量之间与输出变量之间的关系,因为高维输入输出变量的各维度之间本身具有复杂的关联性.同时,将算法的应用领域进行拓展,使其不仅局限于HoG这一特征,甚至不仅局限于人体姿态估计这一问题,而是用于解决更多的结构化预测问题.
