带有不匹配干扰的多智能体系统有限时间积分滑模控制
2019-06-22刘凡杨洪勇杨怡泽李玉玲刘远山
刘凡 杨洪勇 杨怡泽 李玉玲 刘远山
近年来,随着计算机技术、网络通信、控制工程等新兴产业的相互融合与促进,信息物理系统(Cyber-physical system,CPS)随之出现,并朝着大规模、复杂化、智能化的方向发展.多智能体系统分布式协调控制问题作为CPS系统的典型问题,引起了众多研究者的广泛关注.分布式协同控制因效率高、鲁棒性强等优点,被广泛应用于无人机编队控制[1]、多机器人协同控制[2]、多飞行器系统群集控制[3−4]等领域.
一致性问题是多智能体协同控制领域的基本问题,也是协调控制中的研究热点之一[5−13].多智能体系统通过各智能体之间互相协调合作进行信息传递,按照控制协议改变自身的状态,从而使各个智能体达到状态一致.近年来诸多学者已经分别针对一阶、二阶、混合阶以及高阶多智能体系统展开了深入的研究[5−7].考虑到许多自然现象的动力学特性不能用整数阶方程描述,分数阶(非整数阶)动力学的智能个体合作行为也引起了许多研究者的关注[8−9].此外,在解决多智能体系统一致性问题时,常常会遇到存在领导者的情况,这被称为Leader-follower(领导跟随型)问题[10].在多个领导者情况下,多智能体系统的跟踪问题就变成包容控制问题[11−14].这是领导跟随型一致性问题在多个领导者情况下的扩展,跟随者在通信协议的作用下最终收敛到由多个领导者围成的某一目标区域内.文献[13]分别研究了通信拓扑为动态联合联通且存在通信时延情况下二阶网络化系统的包容控制问题.文献[14]研究了具有时延的分数阶多智能体系统的包容控制问题,利用Laplace变换和频域定理,提出了无向网络分数阶多智能体系统包容控制协议.
上述研究成果均是假设多智能体系统中各个智能体的状态渐近达到稳定,即当时间趋于无穷大时,各个智能体的状态可以达到某一共同值.然而在实际应用中,特别是某些控制精度比较高的系统,往往要求系统在很短的时间内能够达成一致.与渐近收敛相比,有限时间一致性控制法不仅可以保证系统的收敛速度更快,在系统存在外部干扰时也表现出更好的鲁棒性[15].因此研究多智能体系统的有限时间一致性是很有实际意义的.目前关于多智能体系统的有限时间一致性问题已取得比较丰富的研究成果[16−18],文献[16]研究了二阶多智能体系统有限时间快速收敛问题.文献[17]研究了带有外部干扰的二阶多智能体系统分布式有限时间包容控制,提出了分布式有限时间包容控制算法使得跟随者的状态在有限时间内收敛到由领导者组成的动态区域内.文献[18]针对联合连通拓扑下具有多领导者的二阶多智能体系统群集运动问题,提出了一种有限时间收敛的包容控制算法.
由于复杂多变的工作环境,多智能体系统通常会受到各种干扰的影响.为了处理系统干扰,研究者提出了许多先进的控制方法,包括自适应控制[19]、鲁棒控制[20],滑模控制[21−22]等.然而大多数方法仅考虑匹配干扰,即干扰与控制输入在同一通道中.在多智能体系统中,常常存在异于控制输入通道进入系统的干扰,即不匹配干扰.不匹配干扰广泛存在于实际工程系统中,例如多导弹系统[23]和工业磁悬浮列车控制系统[24].由于不匹配干扰无法直接利用反馈控制器消除,因此对带有不匹配干扰系统的协同控制的研究意义重大.文献[24]以工业磁悬浮列车控制系统为例,详细介绍了不匹配干扰的成因和影响,基于干扰观测器方法,介绍了状态通道和输出通道不匹配不确定系统干扰主动控制方法.文献[25]提出基于控制的干扰观测器(Disturbance observer based control,DOBC)方法,利用干扰前馈补偿和输出反馈复合控制来消除干扰.文献[26]研究了带有不匹配干扰的高阶多智能体系统分布式主动抗干扰控制方法,结合滑模控制理论和DOBC方法,实现系统的输出一致性.但文中各智能体的状态最终渐近收敛,没有考虑有限时间收敛的情况.文献[27]研究了不匹配二阶多智能体受扰系统的输出一致性问题,文献[28]研究了带有不匹配干扰的多智能体系统有限时间包容控制问题.这两篇文献对系统模型作了处理,将不匹配干扰转变成匹配干扰,从而可以利用常规的处理方式消除干扰.然而在实际应用中存在很多情况不能如此处理,因此该方法有一定的局限性.文献[29]研究了基于扰动观测器的复合积分滑模制导律设计,给出一种基于积分滑模控制理论和非线性扰动观测理论的复合制导律方法,但是该方法没有考虑到系统中存在不匹配干扰的情况.
本文以文献[24]介绍的不匹配干扰为研究对象,研究带有不匹配干扰的二阶多智能体系统的有限时间包容控制问题.相对于文献[27−28],本文的创新点在于设计了主动有限时间干扰观测器直接估算智能体的不匹配干扰,并在控制协议中做出干扰补偿,提出了较为新颖的复合分布式积分滑模控制律.应用滑模控制和现代控制等相关理论,研究了具有不匹配干扰二阶多智能体系统的有限时间包容控制问题.
1 预备知识
1.1 代数图论
假设n个节点的权重连接图用G=(V,E,A)来表示,其中V={v1,v2,···,vn}为n个节点的集合,节点的下标集合N={1,2,···,n},E⊆V×V为边的集合,A=[aij]∈Rn×n为图G的权重邻接矩阵,其中矩阵元素aij表示节点vi与节点vj的连接权重.定义Ni={vj∈V|(vi,vj)∈E}为节点vi的邻居集合.当vj∈Ni时,aij>0,否则aij=0.若对∀i∈N,aij=aji,j∈N,则图G为无向拓扑图,且邻接矩阵A为对称矩阵.若对∀i∈N,aij6aji,j∈N,则图G为有向拓扑图,且邻接矩阵A为非对称矩阵.假设图G中任一节点无自环,即对于∀i∈N,aii=0.定义D为图G的度对角矩阵D=diag{d1,d2,···,dn},其中节点vi的度.图G的Laplacian矩阵定义为L=D−A.无向联通拓扑图的Laplacian矩阵为对称矩阵.
1.2 相关引理和定义
引理1(Input-to-state stability theorem,ISS)[30].考虑非线性系统,如果系统是全局均一化指数型稳定,当limt→∞u(t)=0时,系统的状态渐近收敛到0,即limt→∞x(t)=0.
引理2[15].考虑系统,f(0)=0,x∈Rn,假设存在一个正定连续函数V(x):U→R,且实数c>0,α∈(0,1),在U0⊂U的邻域上满足,,则V(x)在有限时间内收敛到0.此外有限时间T满足T≤.
定义1[12−13].假设集合X是向量空间的子集,集合X的凸包定义为.
定义2[15,18].考虑连续非线性系统:,x(0)=X0∈Rn,其中连续向量流f(X)=[f1(x),f2(X),···,fn(x)]T与带有扩张r=[r1,r2,···,rn],ri>0的度κ∈R是齐次的,如果对于任意的ε>0,x∈Rn都有fi(εr1x1,εr2x2,···,εrnxn)=εκ+rifi(X),i=1,2,···,n.
引理3[15,18].若系统, x(0)=X0∈Rn与带有扩张r=[r1,r2,···,rn],ri>0 的度κ∈R是齐次的,函数f(X)是连续的,且X=0是其一个渐近稳定平衡点.如果齐次度κ<0,则该系统是有限时间稳定的.
定义3.如果网络化系统中的一个自主体至少存在一个邻接成员,则称之为跟随者,否则称为领导者.
2 二阶多智能体系统的有限时间包容控制
假设一个具有n个跟随者和m个领导者的多智能体系统,其中每个智能体可理解为加权无向图G中的一个顶点,各智能体之间的信息传递可理解为图G的边.考虑二阶多智能体系统未受到干扰时的动力学模型为
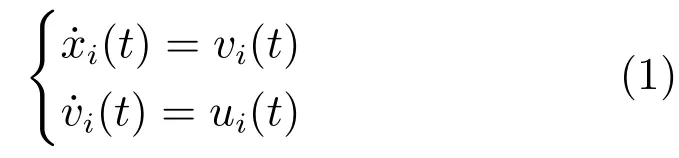
其中,i={1,2,···,n,n+1,···,n+m},n表示跟随者的个数,m表示领导者的个数,跟随者和领导者集合分别表示为F={1,2,···,n}和L={n+1,n+2,···,n+m}.xi(t)和vi(t)分别表示系统第i个智能体在t时刻的位置和速度,ui(t)是控制输入.假设领导者为作匀速运动的动态领导者,对于∀i∈L,其动力学模型为

多Leader-follower型多智能体系统(1)和(2)的通信拓扑图可描述成Gn+m=(Vn+m,En+m,An+m),其中m表示领导者的个数,n表示跟随者的个数.图Gn+m的邻接矩阵为An+m=[aij]∈R(n+m)×(n+m),Laplacian 矩阵为Ln+m=[lij]∈R(n+m)×(n+m),可描述成,Lf∈Rn×n,Ld∈Rn×m.
假设1.领导者相互间不通信,领导者与跟随者之间单向通信,跟随者之间为双向通信,且每个智能体都可接收到它邻居发送的状态信息和干扰估计信息.
假设2.多Leader-follower型多智能体系统的通信拓扑Gn+m包含至少一条有向生成树.
引理4[12].如果假设2成立,多Leader-follower型多智能体系统的Lf是正定的,此外−L−f1Ld为非负的且行和为1.

基于上述描述,本节首先考虑不存在干扰的情况,设计分布式控制协议,使得各个跟随者的状态在有限时间内实现包容控制,即xi→Co{xj,j∈L}.
首先令跟踪误差为

基于跟踪误差(3),设计控制器如下:
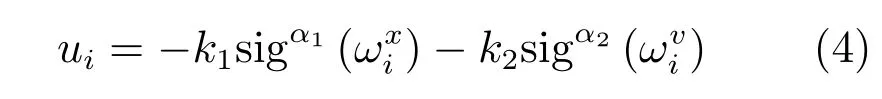
其中,控制增益k1,k2>0,0<α1<1,α2=2α1/(α1+1).sigα(xi)=|xi|αsgn(xi),sgn(·) 表示符号函数. 假设 sigα(x)=[sigα(x1),sigα(x2),···,sigα(xn)]T.
定理1.考虑由n个跟随者和m个领导者组成的二阶动态多智能体系统(1)和(2),其通信拓扑图可描述成Gn+m=(Vn+m,En+m,An+m),如果假设1和假设2成立,则多智能体系统基于分布式控制协议(4)可实现全局有限时间包容控制.
证明.由引理4可知,多智能体系统(1)和(2)的Lf是正定的.令,则跟踪误差(3)转变成矩阵形式为
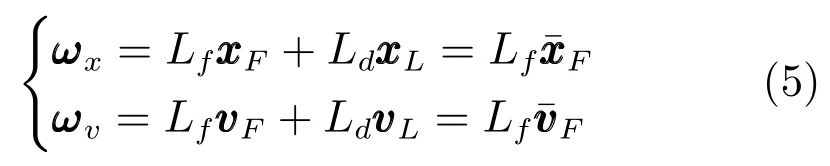

构造Lyapunov函数
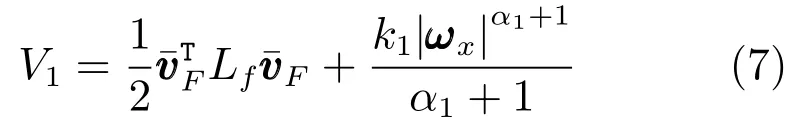
对V1函数沿着式(6)求一次导,得
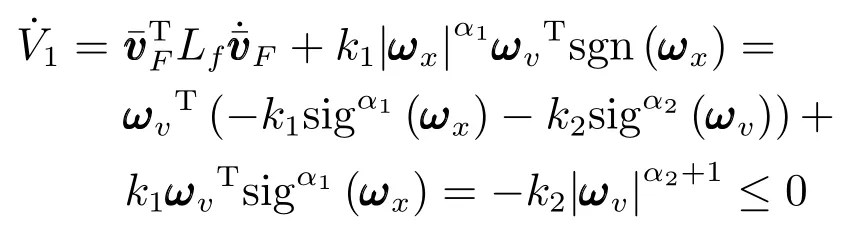
下面分析系统的齐次性.假设原动力学系统为

取r1=2,r2=1+α1,κ=α1−1,则有

综上可知,多智能体系统(1)和(2)可实现有限时间包容控制.□
3 带有不匹配干扰的多智能体系统的有限时间包容控制
本节考虑二阶多智能体系统中存在的不匹配干扰和匹配干扰等多源干扰的情况,假设二阶受扰多智能体系统的动力学模型为

其中,i∈F={1,2,···,n},n表示跟随者的个数,xi(t)和vi(t)分别是智能体的位置和速度,ui(t)是控制输入,di1(t)和di2(t)分别表示不匹配干扰和匹配干扰.
领导者的动力学模型为

其中,j∈L={n+1,n+2,···,n+m},m表示领导者的个数,xj(t)和vj(t)分别是领导者位置和速度.
为了解决系统(9)中的不匹配干扰并保持系统的标称性能,本节将结合积分滑模控制和非线性干扰观测器给出复合分布式控制协议.首先,通过设计非线性干扰观测器,在有限时间内估算出系统的状态和干扰信息.然后,基于干扰估计值,设计出带有前馈补偿项的复合分布式积分滑模控制协议.
3.1 非线性干扰观测器设计
假设3.干扰dik(t)和,k=1,2,都是有界的.
注1.假设3在DOBC领域是很常见的假设.一方面,如果干扰具有很快时变,那么干扰观测器很难进行估算;另一方面,在实际应用上,有很多种干扰满足这种假设,例如:常值干扰,谐波干扰等[27−29].
引理6[31].对于一般系统

其中,x为状态量,u为控制量,d为系统干扰,f,g已知.设计的非线性干扰观测器如下:

其中,增益λ1,λ2>0,和分别是状态x和干扰d的估计值,则该观测器是有限时间收敛的.
根据引理6,设计干扰观测器如下:

其中,i∈F,分别是系统中跟随者的位置状态和速度的估计值,分别是干扰的估计量,zi1和zi2为中间量,λi1,λi2,λi3,λi4>0 为观测增益.
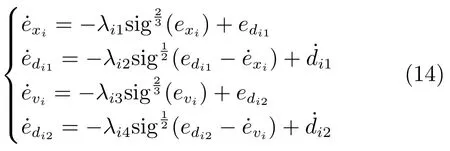
3.2 复合式分布式控制律设计
下面基于上述设计的有限时间干扰观测器,结合滑模控制理论,设计复合分布式控制协议消除干扰,并使得系统(9)和系统(10)实现有限时间包容控制.
首先令跟踪误差为

基于跟踪误差(15),设计复合分布式控制协议如下:
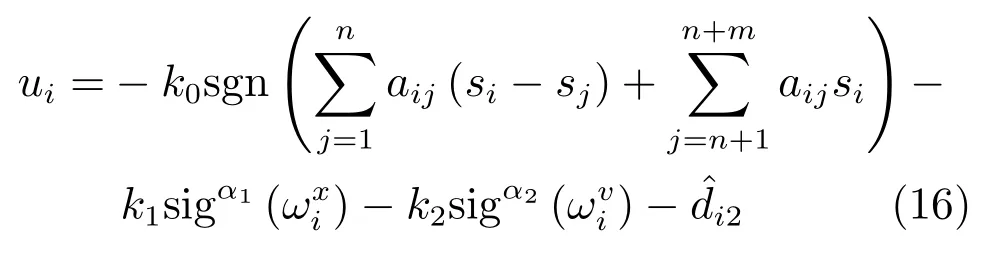
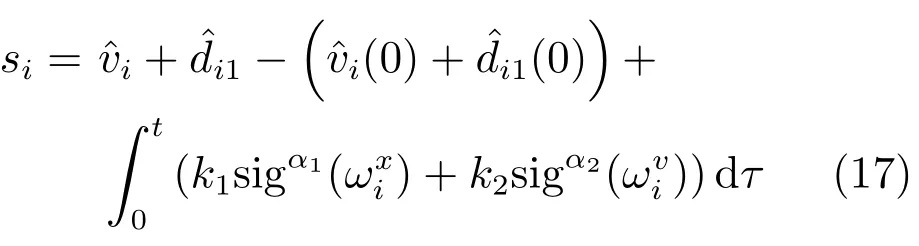
其中,0<α1<1,α2=2α1/(1+α1).当t=0时,si(0)=0,表示各智能体的状态从初始时刻就位于非线性滑模面(17)上.
定理 2.考虑由n个跟随者和m个领导者组成的二阶受扰多智能体系统(9)和(10),其通信拓扑图可描述成Gn+m=(Vn+m,En+m,An+m),如果假设1~3成立,当切换增益满足k0>δ时,基于有限时间干扰观测器(13)和非线性积分滑模面(17)的复合分布式非线性积分滑模控制协议(16)可使得系统实现全局有限时间包容控制.其中,.
证明.首先对滑模面(17)求一次导,得

令S=[s1,s2,···,sn]T,将上式转换成矩阵形式
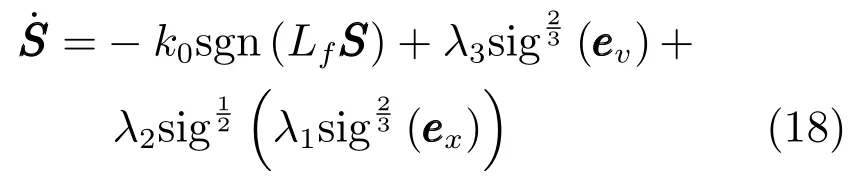
其中,Lf为系统的Laplacian矩阵,λ1=diag{λ11,λ21,···,λn1},λ2=diag{λ12,λ22,···,λn2},λ3=diag{λ13,λ23,···,λn3},ex=[ex1,ex2,···,exn]T,ev=[ev1,ev2,···,evn]T.


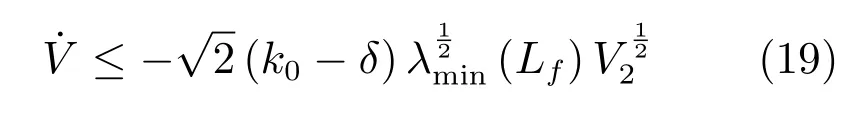
因此,当k0>δ时,由引理2可知各智能体状态可在有限时间内到达非线性滑模面(17)上.假设各智能体状态可在t1时刻到达滑模面上,由引理2可得

式(20)表明各智能体状态从初始时刻开始就一直发生在非线性滑模面上.
下面证明系统有限时间包容控制.首先假设跟随者的状态跟踪误差为.
由有限时间观测器(13)可知,存在一个时刻T∗,当t>T∗时,exi=edi1=evi=edi2=0.因此,闭合系统(9),(10),(16)的有限时间稳定性可分两步证明,即[0,T∗]上状态跟踪误差有界,及t>T∗时,全局有限时间收敛.
1)注意到系统的状态一直发生在非线性积分滑模面上,因此


应用ISS稳定性引理,假设evi,edi1=0,则系统(22)转变为

由定理1可知,系统(23)是有限时间包容控制的,结合引理1,系统(22)是ISS稳定的.由观测器可知,在[0,T∗]内evi和edi1有界,因此系统(22)状态跟踪误差有界.而假设1中说明di1是有界的,因此也是有界的,所以速度跟踪误差是有界的.
2)(全局有限时间包容控制)当t>T∗时,.令,则

由定理1可知,系统可实现全局有限时间包容控制,即在有限时间内.□
注2.文献[26]研究了带有不匹配干扰的高阶多智能体系统分布式主动抗干扰控制方法,同时采用了滑模控制理论和DOBC方法,然而文献[26]设计的是常规的线性滑模面,会出现抖振现象,而本文设计的非线性积分滑模面不仅能有效消除抖振,而且能增强系统的鲁棒性能.文献[27−28]在研究带有不匹配干扰的多智能体系统时对系统模型进行了处理,假设不匹配干扰二阶可微,则可将不匹配干扰转变成匹配干扰,然后利用常规的处理方式消除干扰.但在实际应用中存在很多情况不能如此处理,因此这种方法有一定的局限性.本文则直接对干扰进行观测,并在控制器中添加干扰补偿项,可有效抵消干扰的影响,而不影响系统的性能.
4 数值仿真
考虑4个跟随者和3个领导者组成的网络,如图1所示.
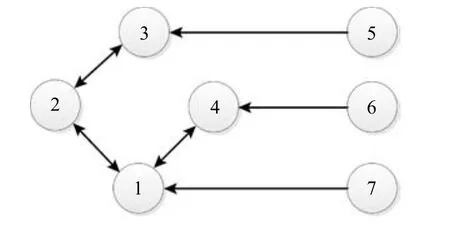
图1 多智能体系统网络拓扑图Fig.1 The network topologies of multi-agent systems
图1中节点1~4是无向连通的跟随者,节点5~7是单向发送信息的领导者.假设拓扑图所有边的权重都是1,则系统的Laplacian矩阵为

其中,

假设4个智能体都受到干扰影响:智能体1:d1,1=2tanh(2t),d1,2=2;智能体2:d2,1=4tanh(t),d2,2=1;智能体3:d3,1=sigmoid(t),d3,2=2sigmoid(2t);智能体4:d4,1=3sigmoid(t),d4,2=−tanh(t),t>0.其中di1,di2(i=1,2,3,4)分别表示不匹配干扰和匹配干扰.
控制器的参数设置为k0=10,k1=20,k2=30,α1=0.8.干扰观测器的参数设置为λi,1=10,λi,2=20,λi,3=15,λi,4=32,i=1,2,3,4;假设 4个跟随者的初始位置分别为x1=(2,0),x2=(4,0),x3=(0,2),x4=(0,4),领导者的初始坐标分别为x5=(6,8),x6=(8,8),x7=(8,6).领导者为动态领导者,其初始速度为v5=(1,1),v6=(1.2,1.2),v7=(1,1).仿真结果如图2~4所示.
图2是干扰观测器(13)对受扰系统(9)中各智能体的不匹配干扰和匹配干扰的观测量和估计误差,从图2(a)和2(c)可以看出观测器可以快速估计出智能体所受的干扰,在图2(b)和2(d)中各智能体所受干扰的观测误差很快的趋于0,说明观测器可准确地估算出系统中的干扰,表现出较好的观测性能.图3是智能体的位置和速度状态观测误差.从图3可知,在不到1s的时间误差曲线趋于0,直观地说明观测器可快速准确地估算出跟随者的状态信息,从而确保控制器的有效作用.
图4是多智能体系统的位置状态轨迹图,其中星号表示跟随者,圆圈表示动态领导者,可以看出3个动态领导者以一定的速度沿着某一方向移动,而4个跟随者通过相互作用最终收敛到有领导者组成的几何体中.特别地,当t=5s时,跟随者还没有完全进入凸包内,而当t=10s时,各跟随者均进入凸包内,且跟随着领导者同步运动.因此,在控制律(16)下各智能体能够快速地跟踪到领导者,并进入由领导者组成的几何体中,实现了包容控制.
文献[26]研究的是带有不匹配干扰的多智能体系统滑模控制.为了进一步说明本文方法的优越性,本文将文献[26]所提方法拓展到多领导者情况.利用上述数值参数,得到图5所示的仿真图.由图5可知,当t=10s时跟随者没有完全进入凸包内,当t=20s时,系统才实现包容控制.与文献[26]的实验结果比较,说明本文方法可以更加快速地达到一致,取得较好的结果.
综上,带干扰的多智能体系统(9)和(10)通过有限时间干扰观测器(13)快速地估算干扰,在复合分布式控制协议(16)下快速消除干扰,使得各跟随者的状态收敛到由动态领导者组成的动态凸包内,即xi→Co{xj,j∈L},实现了包容控制.
5 结论
本文研究带有不匹配干扰的二阶多智能体系统协同控制问题.设计了非线性有限时间干扰观测器,使得智能体的干扰可被观测和补偿.利用滑模控制理论和基于控制的干扰观测器方法,提出了复合分布式非线性积分滑模控制协议.通过使用Lyapunov稳定性理论、代数图论、齐次性理论等方法,研究了带有不匹配干扰的多智能体系统有限时间包容控制.最后数值仿真表明了所提控制算法的有效性.
由于复杂多变的工作环境,多智能体系统通常会受到各种干扰的影响.在实际工程应用中,不匹配干扰是十分常见的干扰,因此本文所提方法具有一定的发展前景,而且更具有普适性.未来的研究方向?将针对更为复杂的环境,设计新型的干扰观测器,研究多智能体系统的协同控制问题.
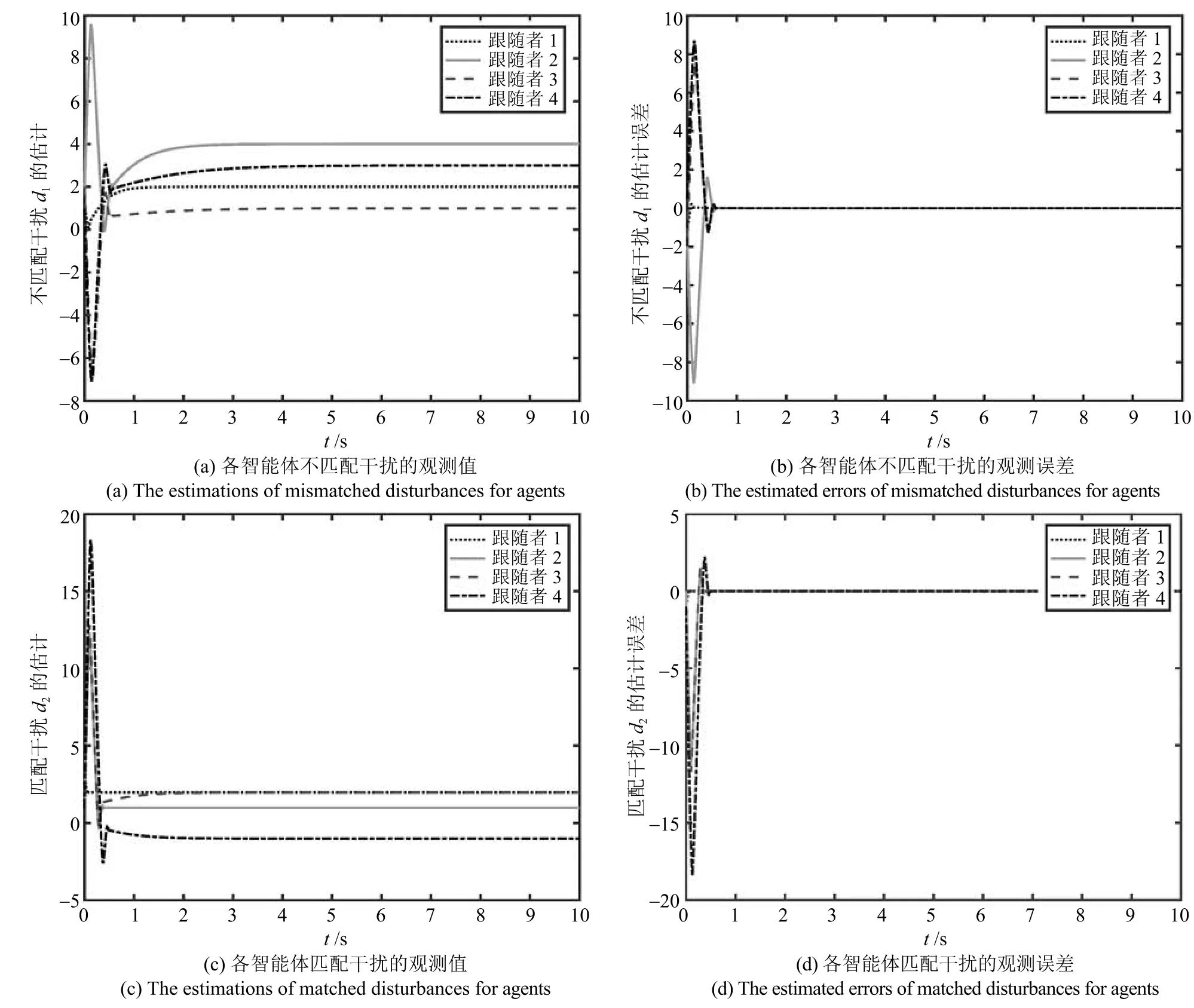
图2 干扰观测器(14)的观测值及观测误差Fig.2 The estimations and estimated errors of DO(14)
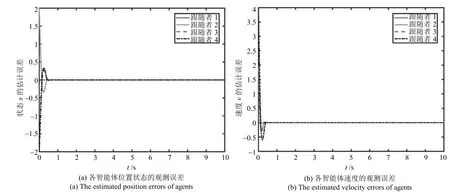
图3 各智能体状态观测误差Fig.3 The estimated state errors of each agent

图4 跟随者与动态领导者的位置关系Fig.4 The trajectories of position for the followers and dynamic leaders
