指向高阶思维命题,促进学生真实学习
2019-06-21付才喜
付才喜

摘 要:为了提高小学数学教师的命题水平,使得平时的数学练习题和考试试题真实地检测出学生的学习水平,满足不同水平的学生,在此背景下,文章以人教版小学数学教材的知识点为例,通过让学生写下思考过程、让学生学会开放性答题、让学生学会选择方法、让学生解决生活问题等途径,命出指向高阶思维的好题,促进学生真实学习。
关键词:数学命题;人教版;高阶思维
数学命题是小学数学教师在教学过程中检测学生对数学知识掌握程度的一种手段,教师有条理地将一些相关知识的数学题目通过改编或者原创等方式组合在一起,了解学生对知识的掌握情况和灵活运用的能力。因此,我们数学教师在编制一张数学试卷时,既要关注数学基础知识,让每个学生都掌握必须的基础知识;又要关注数学拓展知识,让学有余力的学生能挑战难题,体验到学习数学的成功感。
但是,从当前的小学数学试卷来看,有的选择题和填空题偏难,虽然有的学生答案正确,但他们只是靠运气蒙对了答案,而这样的数学命题不能真正检测出学生真实的掌握情况。于是,笔者开始思考怎样的高阶思维命题能区分学生的数学思维,了解学生的思考过程。
一、高阶思维命题,让学生写下思考过程
教师要求学生在试卷上写下自己的思考过程,不仅有利于教师了解学生的解题过程,更有助于学生回顾反思自己的思考过程。如在教学人教版四年级下册第六单元“小数的加法和减法”后,为了考查学生对小数加法到底是末尾对齐还是小数点对齐的理解情况,笔者出了一道数学题,让学生写出自己的理由。
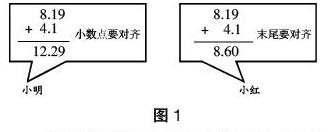
题目是这样的:一个铅笔盒8.19元,一套尺子4.10元,一个铅笔盒与一套尺子共多少元?下面分别是小明和小红的方法(图1),你同意哪个?写出你的理由。
笔者为了区分学生的解题水平,将正确答案“同意小明的作答”分为三种不同的解题水平:(1)0分水平,空白(包括画去或擦除,零散的标记,字迹模糊,或与题目无关)和只要判断错误,无论理由对错;(2)2分水平,判断正确,理由错误,如小数点对齐了,才能算正确;算出答案是小明对;(3)4分水平,答出“相同数位对齐”,或“个位和个位对齐,十分位和十分位对齐,百分位和百分位对齐”,或答出小数点对齐,但是相同数位对齐是具体描述,意思是对的。
又如在教学人教版三年级下册第五单元“长方形的面积”后,笔者为了了解学生对比较面积大小的掌握情况,引导学生把比较面积大小的思考过程写下来。
题目是这样的:东东和明明用相同的小棒擺图形,下面是他们摆出的形状(图2)。东东认为他摆出的图形面积更大,你觉得他说得对吗?把你的结论和思考过程写下来。
同样,这道题目的正确答案是“不对,因为他们摆出的图形都是由同样的两个正方形和一个三角形组成的”。为了区分学生的解题水平,笔者将学生上交的答题分为四种水平:(1)0分水平,学生空白不作答或者判断错误;(2)2分水平,判断正确,但是没有理由或理由不正确;(3)3分水平,判断正确,但是理由部分正确,或比较笼统;(4)判断和理由都正确。
通过以上两个让学生写思考过程的数学命题,我们发现这样的命题方式无论在平时练习中还是在考试中都是极有必要的,它反映出我们在平时的数学课堂上要给予学生严密且规范说理的模版,并且让学生在小组内和班级里多相互评议说理中存在的问题,提高学生的数学语言表达能力。
二、高阶思维命题,让学生学会开放性答题
开放性答题,是让学生综合性地梳理较多的数学知识,用合理且自圆其说的方式解决数学问题。如在教学人教版六年级下册第三单元“圆柱和圆锥的体积”知识后,笔者给学生出了一道题:一张A4纸的长是29.7厘米,宽是21厘米,把这张A4纸旋转一周后形成圆柱体,请你计算圆柱体的体积。此时,有的学生只考虑了一张A4纸一边旋转后形成的圆柱体,因此我们要学会分类思考:如果是用长边旋转后形成的圆柱体,那么这个圆柱体的体积是V=Sh=π×21×21×29.7=13097.7π(立方厘米);如果是用短边旋转后形成的圆柱体,那么这个圆柱体的体积是V=Sh=π×29.7×29.7×21=18523.89π(立方厘米)。
又如:在教学人教版六年级下册第二单元“百分数”的知识后,笔者出了一道实践性作业题:一家4口(2个成人,2个儿童)去某地旅游,甲旅行社的收费标准是:如果买3张全票,则剩下的人按半价购票;乙旅行社的收费标准是:购买家庭旅游套票按原价的80%优惠,每张旅游票的原价是每人1000元,你会选择哪家旅行社?通过计算说明你的理由。这是一道让学生利用数学知识解决生活问题的开放题,使学生在运用百分数知识解决问题时学会选择。
开放性的数学命题能开拓学生的数学思维,充满着现实性与挑战性,学生会带着自己的个性创造性地完成这些题目,培养了学生的创造性思维。
三、高阶思维命题,让学生学会选择方法
一道好的数学命题,能够考查学生的数学思维能力,包括该生数学思维的深刻性、灵活性、敏捷性、批判性、独创性和系统性。如在教学人教版四年级上册第四单元“路程速度时间”一课后,笔者出示了一道数学练习题:甲、乙两地相距504千米,一辆汽车从甲地开往乙地,6小时行了全程的,以这样的速度,还需几小时到达乙地?仔细阅读这道题目后,大部分学生都利用路程、速度、时间的关系,先计算出全程的是504×=378(千米),再计算出这辆汽车的速度是378÷6=63(千米/时),接着计算出剩下的路程是504×=126(千米),最后计算出剩下的路程需要的时间是126÷63=2(时)。同样是利用路程、速度、时间的关系来答题,有的学生先计算出全程的、这辆汽车的速度,接着计算出全程所需要的时间是504÷63=8(时),最后计算出剩下的路程需要8-6=2(时)。但是,也有学生的解题思路与众不同,他们抓住路程与时间的比值相同,计算出剩下路程所需要的时间是÷(÷6)=2(时)。
又如笔者在教学人教版四年级下册第三单元“运算定律”后,为学生命制了一道简便计算题:9+19+29+39+49,有的学生按照题目依次口算;有的学生把这些数看成整十数,因此就有了9+19+29+39+49=10+20+30+40+50-5=145;有的学生把每个数拆成整十数部分和9,于是就有了9+19+29+39+49=9+10+9+20+9+30+9+40+9=10×10+9×5=100+45=145;还有的学生把这些数都看成29,那么9+19+29+39+49=29×5-10-20+10+20=29×5=145。
通过以上两个数学命题,我们看到学生对于同一道题目会采用不同的解题方法,学生适时体会到数学方法的简洁美。
四、高阶思维命题,让学生解决生活问题
2011年版《小学数学新课标》中特别强调:“数学源自生活,又为生活服务。”为了在数学命题中让学生感受到生活中处处都有数学,笔者在教学人教版三年级上册第五单元“倍的认识”一课后,命制了一道综合性的生活数学问题:有以下六个条件:(1)冲冲今年8岁;(2)舅舅比妈妈小2岁;(3)外公的年龄是冲冲的8倍;(4)外公28岁时妈妈出生;(5)舅舅比舅妈大2岁;(6)外婆比舅舅大26岁,请问外婆今年多少岁?为了解决这个生活性的数学问题,学生需要学会合理地选择数学条件和数学问题,掌握和建立关联的方法,辨别相关与无关的信息,利用关联顺序解决问题。他们需要在这六个数学条件中先筛选组合出有用的数学信息是“冲冲今年8岁,外公的年龄是冲冲的8倍,外公28岁时妈妈出生,舅舅比妈妈小2岁,外婆比舅舅大26岁,外婆今年多少岁?”,从而得到要先算出外公的年龄是8×8=64(岁);再根据“外公28岁时妈妈出生”推算出妈妈比外公小27岁,所以算出妈妈的年龄是64-27=37(歲);接着计算舅舅的年龄是37-2=35(岁),最后算出外婆的年龄是35+26=61(岁)。
又如:在教学人教版二年级下册第九单元“数学广角——推理”时,为了检测学生对推理的认知水平,笔者借助生活中的几个学生的对话来命题:以下有五组聊天记录:(1)学校有28个皮球,4个破了;(2)数了数,没破的装了6只盒子,2只打开着的装了8个皮球;(3)学校明天有4个班参加课外活动;(4)我班明天没有课外活动;(5)小红说:“没破的红皮球有12只。”小丽说:“白皮球比红皮球少8只。”小东说:“没破的花皮球是白皮球的2倍。”小青说:“象棋有12副。”请问:一共有多少个皮球?在那么多的数学信息中,学生要区分出与问题有关的信息“学校有28个皮球,4个破了”,从而计算出皮球一共有28+4=32(个)。
通过以上两个生活中的数学命题不难看出,我们要着重引导学生体会数学与生活的紧密联系,在实际生活的聊天语言中我们要学会正确选择有效的数学信息并进行合理的推导。
总之,指向高阶思维的数学命题,要让学生在解答数学题目时学会思考、学会说明、学会辨析,只有从不同的角度经历数学思考过程,才能最终形成高阶思维。
