一道常见高三模考题的解法探究及推广

江苏省灌南高级中学

熊寿权 (邮编：222500)

1 例题呈现

(2017南京模拟试题)△ABC中，a、b、c分别表示角A、B、C的对边.若a2+b2+2c2=8，则S△ABC的最大值为.

这是一道江苏近几年高三会经常碰到的熟题，一般放在填空题压轴位置，但计算量不算太小，因此笔者做了一些研究，希望能得到一些结论.先给出几种常见解法：

解法一△ABC中，a2+b2+2c2=8，

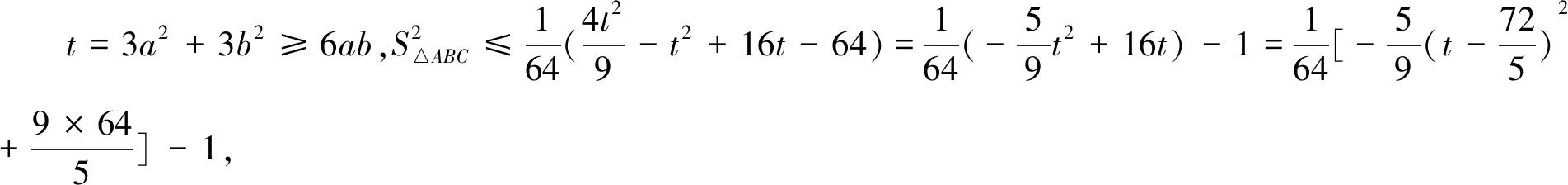
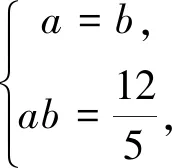
解法二解法一中得到关于a、b的二元四次函数时，也可将其化成以a为主元的一元二次函数先处理再求关于b的函数的最值，本处从略；

解法三在三角形中由余弦定理结合条件有：(b2+c2-2bccosA)+b2+2c2=8，故

解法五(解析法)令条件中的c为定值，则条件变为a2+b2=8-2c2，以AB所在直线为x轴，AB中垂线所在直线为y轴，建立平面直角坐标系.

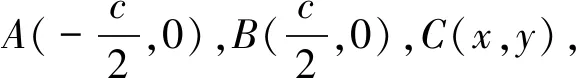
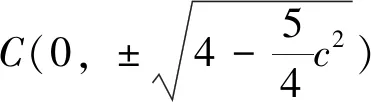
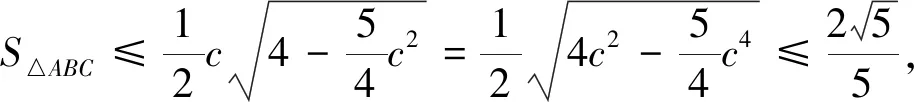
图1

解法六如图所示，设AB边上的高为h，垂足分AB两段长分别为x和y，则AB=c=x+y，

8=a2+b2+2c2=2h2+2c2+x2+y2，

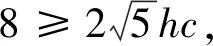
2 本着从特殊到一般的思想，可猜想一般性结论：

△ABC中，a、b、c分别表示角A、B、C的对边.

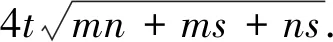
3 反思

在高三繁重的复习过程中，如何通过研究一道题渗透数学思想，培养学生核心素养，当是一线教师必须重视的课题.英国著名数学家哈代曾说过：“严格来说，没有所谓证明这个东西，归根结底，我们只是在指指点点.”数学学科很多东西都是在前人或已知结论的基础上研究新的问题，因此作为高中生特别是高三学生熟悉某些常见结论或方法也显得弥足珍贵了.