剖析命制之瑕疵 在借鉴中创新
2019-06-21福建省仙游县第二道德中学
福建省仙游县第二道德中学
林攀峰 (邮编:351200)
本文以一道改编试题的命制之瑕疵,以及对其如何进行研磨等方面剖析,可以有效地启迪命题者、一线教师们,如何在“情境能力立意,素养导向”下组织发展试题,改编试题如何在教学上数学思维能力的培养能有更好的“关注点”“落脚点”,数学核心素养的内化能真正落地,上下位贯通联系,拓宽维度,拓展深度,实现教与学的良性循环互动.

图1
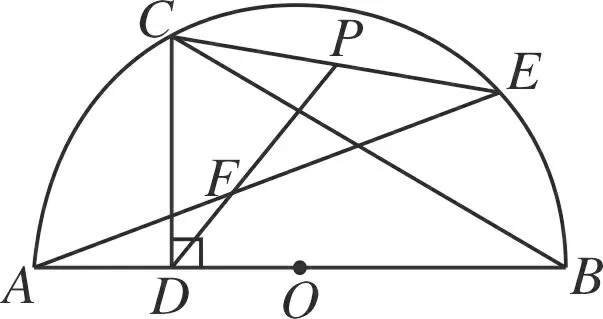
图2
1 原题呈现


(2)如图2,若∠B=30°,连接CE,点P为CE的中点,连接DP,交AE于点F,记以C为圆心,CP为半径的圆为⊙C.判断AE与⊙C的位置关系.并说明理由.
实测情况

题号分值平均分难度/得分率区分度24123.950.330.47
学生反映第1步没有思路,不知道从何入手,也有学生把(2)步的条件“∠B=30°”拿上来用?第2步,思路直接,结论显而易现,担心做为压轴题这样会不会太简单了,反复深陷在自我怀疑里,不能自拔.
2 试题剖析
2.1 对题(1)的思考
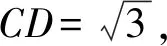



图3

图4

以上两种方法的思路亦可理解为截长补短(法1取AE的中点,法2倍长CD).
2.2 对题(2)的思考

图5

图6
猜想点F是切点(即点G与点F重合),也许这才是命题者想考查的核心知识,因为从条件“连接DP,交AE于点F”亦可知.

图7
验证思路一(证点G与点F重合)
方法1 作CG⊥AE,垂足为G则有A、C、D、G四点共圆连接AC,∠B=30°,有∠CAB=60°,所以∠CGD=120°,连接PG,在Rt△CGE中,∠E=∠B=30°,所以∠CGP=60°,因为∠CGD+∠CGP=180°,所以P、G、D三点共线,即点G与点F重合.
思路二(连接CF,证CF⊥AE)
方法2 连接CA,CF,OP,由OP⊥CE,且CD⊥AB,可得C、D、O、P四点共圆,
所以∠CPD=∠COD=2∠B=60°,
又因为∠E=∠B=30°,所以∠PFE=∠CPD-∠E=30°,则PF=PE,有PF=PE=PC,
所以△CFE是直角三角形,即CF⊥AE.
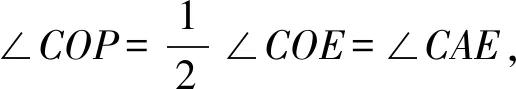
反思由方法3,我们并没有利用条件“∠B=30°”,即这个条件是多余的!
3 改编试题之打磨
(1)借鉴 【试题赏析】
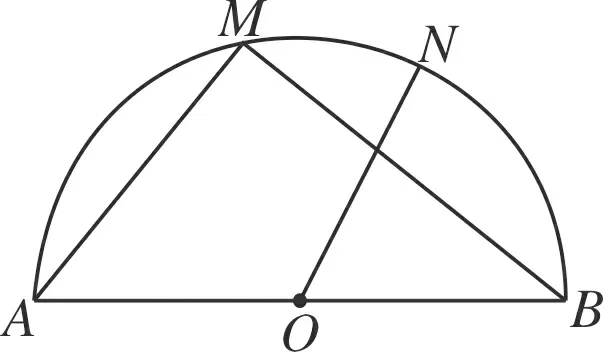
图8
(2017秋·厦门期末)已知AB是半圆O的直径,M,N是半圆不与A,B重合的两点,且点N在弧BM上.
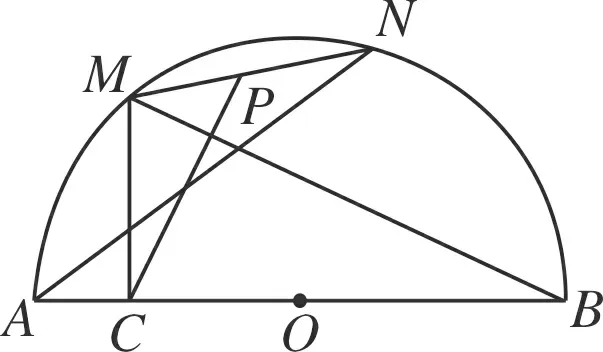
图9
(1)如图8,MA=6,MB=8,∠NOB=60°,求NB的长;
(2)如图9,过点M作MC⊥AB于点C,点P是MN的中点,连接MB、NA、PC,试探究∠MCP、∠NAB、∠MBA之间的数量关系,并证明.

图10
(2)原题议编
如图10,AB是半圆O的直径,C,E在半圆O上(不与A,B重合的两点),CD⊥AB于点D.

图11

(2)如图11,连接CE,若点P为CE中点,连接DP,交AE于点F.判断直线CF与AE的位置关系.并说明理由.
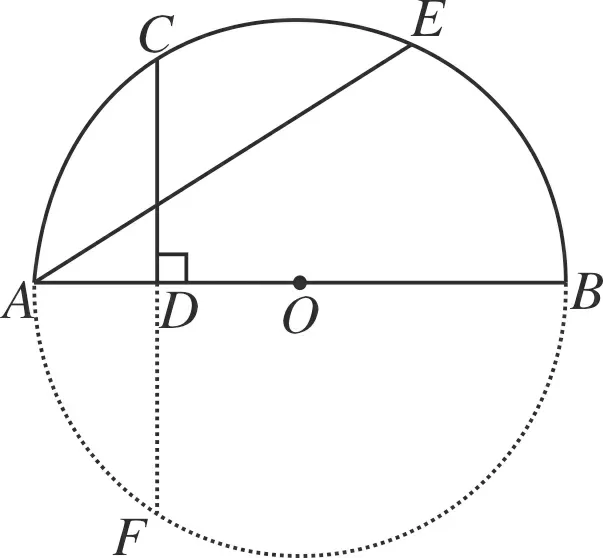
图12

图13

图14
分析从条件“AB是半圆O的直径,从CD⊥AB于点D”入手进行析题
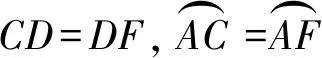

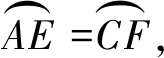
所以AE=CF=2CD.
(2)如图13,因为点P为CE的中点,所以DP是△CNE的中位线,所以DP∥EN,
所以∠AFD=∠AEN=∠ACN,所以C、A、F、D四点共圆,
从而有∠CFA=∠CDA=90°.
思考此时,亦有结论∠EAB+∠CBA+∠CDP=90°成立.
证法如上:
因为∠CDP=∠CNE,∠EAB=∠ENB,∠CBA=∠CNA,
所以∠A+∠B+∠CDP=∠ENB+∠CNA+∠CNE=∠ANB,
因为AB是圆O的直径,所以∠EAB+∠CBA+∠CDP=∠ANB=90°.

4 改编试题之感悟
初中学业水平考试以能力立意与素养导向,加强理性思维考查,体现创新性,对数学核心素养的测量要以知识为基础,以数学思想方法为引领,以情境为载体,注重综合性和层次性,注重考查学生综合运用所学知识分析问题和解决问题的能力,增强与学生生活、社会实际的联系.这些评价建议对命题提出了很高的要求,特别是作为考试的压轴题,对知识、能力、素养、情境的要求更加上位,对教学更具有导向性.
命题从改编入手,若忽视试题中所考查的核心知识,单纯从改变数据或条件的强化(弱化),一味追求技能的叠加,往往会出现试题不严谨的问题.所以析题是关键,只有通过研究优秀试题的编制思路,将其解构、叠加、组合、转化、发展等进行剖析,以期全面深刻地了解和把握该类试题,在此基础上进行改编才能达到传承和创新.
