汽车后扭力梁悬架系统的动态性能优化方法

李 军，李兆军，杨九洲，衡 星

（广西大学机械工程学院，广西 南宁530004）

0 前言

汽车后扭力梁悬架是汽车的一个重要组成部分，其动态性能的好坏直接影响到整车的舒适性和安全性，因而对汽车后扭力梁悬架的动态性能进行优化是十分必要的[1]。目前，国内外对汽车后扭力梁悬架的优化研究主要是根据悬架的静态、动态表现对悬架局部位置进行结构参数的调整。如陈松、廖抒华等学者根据强度分析结果对悬架薄弱位置进行了尺寸参数的调整[2-3]；蒋荣超以质量和疲劳寿命为优化目标，以一阶扭转频率和扭转刚度为约束，条件对悬架进行了优化[4]；娄臻亮提出了一种把性能及其稳健性水平纳入多响应的优化方法，以重量最低为优化目标，综合考虑悬架的多项性能指标得到悬架的优化解域[5]，等等。然而，在路面激励、发动机激励等外激励作用下，汽车后扭力梁悬架的动态性能十分复杂，因而，为了对汽车后扭力梁悬架的动态性能进行优化，有必要建立能够全面反映悬架系统的动态性能与其结构参数、材料参数及外激励参数之间内在关系的动力学方程，揭示悬架系统的振动机理，进而确定悬架系统动态性能优化方法。但目前这方面的研究鲜有文献报道。

因而考虑悬架与汽车其他组件相互作用相互影响的情形，运用有限元法建立汽车后扭力梁悬架系统的动力学方程，探明汽车后扭力梁悬架系统的振动机理，确定汽车后扭力梁悬架系统的动态性能优化方法。

1 汽车后扭力梁悬架系统动力学模型

扭力梁悬架一般都安装于汽车底盘中，主要由纵臂、横梁、减震器及减震托盘、轮毂架及衬套组成，其与汽车车身、轮胎相互连接且相互影响，构成了一个复杂的振动系统。发动机激励通过车身传递到后扭力梁悬架，路面激励通过轮胎直接作用在悬架上。因而为更全面深入地研究悬架的动态性能，有必要将后扭力梁悬架与汽车其他部件组成汽车后扭力梁悬架系统进行研究。为简化模型，对该系统进行如下处理：考虑到发动机机体主要由铸铁、合金铸铁等造成，车桥为刚性实心结构，车身是汽车的主体部件，它们的最低阶模态要高于发动机悬置系统、车桥悬架系统和排气系统吊挂的模态频率，因而相对于汽车后扭力梁悬架而言，可将发动机、车桥、车身简化为刚体；根据汽车动力学，轮胎载荷与垂向变形基本呈线性关系，前悬架用于控制车身和轮胎的刚体模态，且其质量较轻，后减震器用来缓冲路面的冲击，因而可将轮胎、前悬架、后减震器简化为弹簧阻尼单元；对于后悬架上的轮毂支架、减震托盘等一些焊接部件，将其简化等效在对应的纵臂位置的集中质量和刚度，并在计算分析时将其叠加到相应单元质量矩阵和刚度矩阵中来表示。综上，考虑悬架与汽车其他组件相互作用相互影响的汽车后扭力梁悬架系统可简化为如图1所示的动力学模型。

图1 汽车后扭力梁悬架力学系统模型

在汽车的行驶过程中，后悬架主要受到的是横向力。纵臂通过橡胶衬套与车身相连接，在横向力的作用下，纵臂将产生横向弹性位移，又由于纵臂为管状且各截面大小相近似不变，因而这里采用等截面梁单元来模拟纵臂。对于横梁而言，由于受到横向力的作用，因而会产生横向弹性位移，同时，横梁还会受到左右轮传递过来的作用力，当左右轮传递过来的作用力大小不同时，将会导致横梁产生扭转变形，又由于横梁一般为半管状的变截面结构，因而这里采用变截面轴单元来模拟横梁。根据有限单元法即可建立汽车后扭力梁悬架系统的动力学方程，即

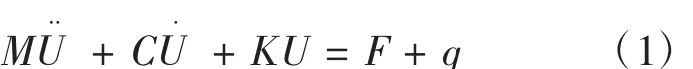
式中，M为系统的质量矩阵；K为系统的刚度矩阵，C为系统的阻尼矩阵，U为系统整体坐标下的广义坐标向量，U.为整体坐标下的广义速度向量，U..为整体坐标下的广义加速度向量，F为发动机激励向量，q为路面激励力向量。

显然，式（1）反映了汽车后扭力梁悬架系统的动态性能与结构参数、材料参数及外激励参数之间的内在关系，根据所建立的动力学方程，即可对汽车后扭力梁悬架系统的动态性能进行分析和研究。

2 动态性能分析

2.1 外激励特性

2.1.1 路面激励特性分析

当前，路面激励一般是以路面不平度来表示，根据文献适用于实测道路谱的谐波叠加法表示的路面激励数学模型为[6]：

式中，Gq（fmid-i）为路面不平度系数；fmid-i为时间频率f1＜f＜f2范围内划分的第i个中心时间频率；Δfi为第 i个中心时间频率带宽；θ为（0，2π）上均匀分布的相互独力的随机变量。

根据式（2）可知，路面不平度系数及激励频率很大程度上决定了路面激励的大小，而由f=Nua可知，车速与路面空间频率则影响了路面激励频率的范围，在常速ua=10～34 m/s范围内路面激励频率为0.374～28.3 Hz。汽车的行驶工况是复杂多变的，以不同车速行驶在不同的路况下极易引起汽车后扭力梁悬架系统发生激烈振动，进而加速振动疲劳的发生。

2.1.2 发动机激励特性分析

根据文献，对于四缸四冲程发动机而言，发动机惯性力Fw可表示为[7]：

式中，mw为往复惯性质量；Rw为曲轴半径；λw为曲柄连杆比；αw为曲柄转角；ωw为曲轴角速度，ωw=nπ/30且，n为发动机转速。

发动机振动引起的倾覆力Wq矩为[7]：

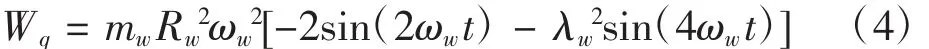
结合式（3）与式（4）可见，发动机激励的大小与其转速有正比的关系。而根据文献又可知，发动机激励频率Ω=n/30，对于转速在800～5 000 r/min范围内的发动机而言，那么其激励频率在26.67～166.67 H z范围内。

2.2 振动特性

2.2.1 固有频率

路面工况的复杂及发动机转速的变化使得外激励频率覆盖范围之广。为分析悬架在外激励作用下是否发生共振，因而有必要对汽车后扭力梁悬架系统进行模态分析。根据机械振动学，自然模态是系统本身的固有属性，振幅在各自由度都是按照对应的自由模态下的振型进行分配的。因而，根据式（1）考虑无阻尼自由状态下的系统振动方程为：

系统作同步运动，将刚度矩阵和质量矩阵代入式（5）得：

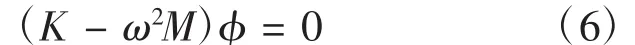
式中，φ为振型矢量。方程（6）是一组关于φ的n元线性齐次方程组，其非零解的条件为系数行列式必须等于零，因而有：

式（7）为频率方程，对其展开求解即可得系统各阶固有频率。

2.2.2 动态响应

为探明外激励作用下汽车后扭力梁悬架系统的动态响应分布规律，根据机械动力学，利用振型叠加法对方程（1）进行求解，即可得汽车后扭力梁悬架系统位移响应U为：

式中，ηr为振型坐标，φr为模态矢量。

3 动态性能优化

3.1 动态灵敏度分析

灵敏度分析用于定量预测结构参数变化对结构动态性能的影响，在系统辨识以及结构优化等研究中非常重要[8]。灵敏度值绝对值越大表明该结构性能对该参数越敏感。因而为使系统固有频率尽可能远离外激励频率以防止系统发生共振，有必要对固有频率进行灵敏度分析，根据文献[9]，第r阶固有频率ωr对设计变量xj的灵敏度为：

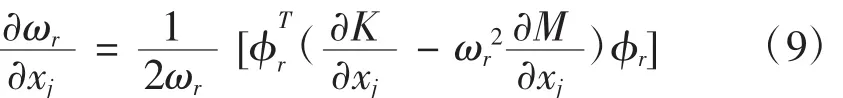
由于刚度矩阵和质量矩阵都和结构参数、材料参数相关，因而根据式（9）可分析任意一阶固有频率对相关设计变量改变的敏感度。

动态响应是直接反映动态性能的主要指标之一，为使汽车后扭力梁悬架关键位置的动态响应合理分布，有必要对关键位置位移响应进行灵敏度分析，根据式（8），系统广义坐标向量U中的第i个广义坐标Ui对设计变量xj的灵敏度为[8]：

3.2 动态性能的优化

在汽车后扭力梁悬架中，横梁与纵臂往往是通过焊接相连接，横梁与纵臂连接处非常容易出现脱焊[10]，若该处出现脱焊，就会影响后扭力梁悬架的安全可靠运作。由于汽车后扭力梁悬架的振动是导致其产生脱焊的主要原因之一，因而为了延长其使用寿命，有必要对横梁与纵臂连接处的动态性能进行优化。

这里以汽车后扭力梁悬架系统的结构参数为设计变量，横梁与纵臂连接点动态响应峰值最小为目标函数，给定频率范围为约束条件，建立汽车后扭力梁悬架系统的优化数学模型为：

式中，ωi为系统第i阶固有频率；pi为外激励频率；xl，xu为设计变量的上下界限；c为汽车后扭力梁悬架系统频率经验系数。

式（11）所示的优化设计模型有边界约束及性态约束，为克服尺度变换带来的繁琐，综合优化设计理论，结合导重法[11]对后扭力梁悬架进行动态性能优化。

4 实例仿真分析

某车型扭力梁悬架的纵臂和横梁材料均为SPFH590，弹性模量E=2.068×1011，泊松比μ=0.3，密度ρ=7.85×103kg/m3。其中纵臂厚度为4.5 mm，长度为420 mm，横梁厚度为3 mm，长度为1120 mm，且横梁焊接在纵臂自车身连接点起的190 mm位置处。该车型其他模型参数如表1所示。

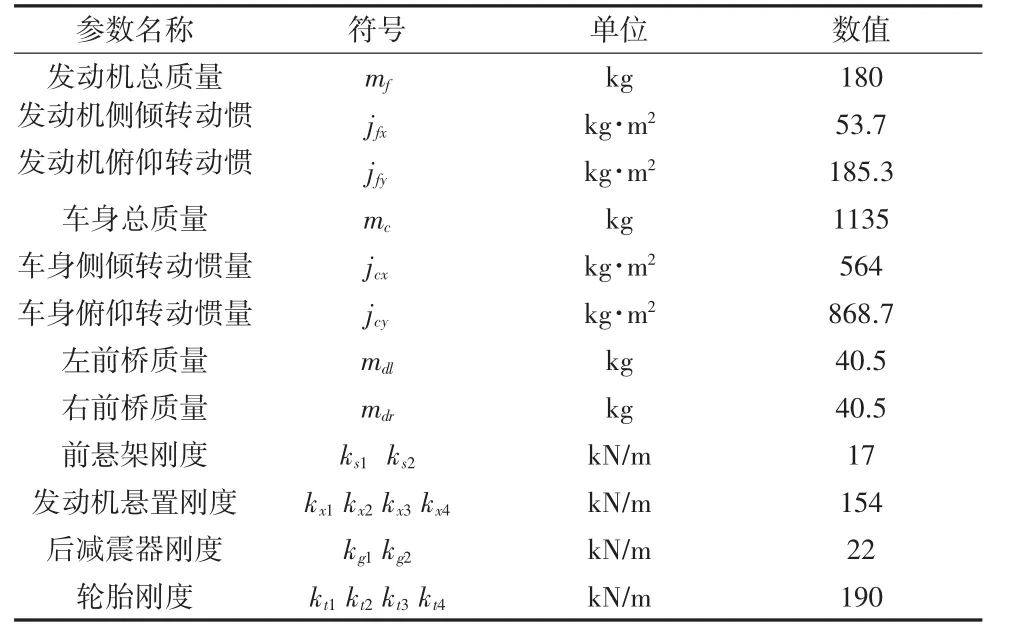
表1 汽车模型参数

根据式（7），利用MATLAB软件编程，对汽车后扭力梁悬架系统固有频率进行求解，其前6阶固有频率数值如表2所示。

表2 汽车后扭力梁悬架系统固有频率

根据前面的外激励特性分析，在发动机转速范围内，其激励频率为26.67～166.67 Hz覆盖到系统的前5阶固有频率，而路面激励频率0.374～28.3 Hz，一定工况下能接近系统的一阶固有频率，因而在外激励作用下系统就极有可能发生共振。但工作时发动机大多处于经济转速状态2 000～3 500 r/min[12]，由Ω=n/30可知在经济转速范围内Ω=66.67～116.67 Hz覆盖到系统的第二阶固有频率且接近系统的第三阶固有频率。因而这里主要针对系统的前三阶固有频率进行分析。

根据扭力梁悬架的结构特点，这里以纵臂厚度tz、横梁厚度th、横梁与纵臂连接点的位置lh作为设计参数，即

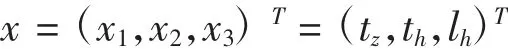
根据式（9）及式（10）计算可得系统前三阶固有频率及横梁与纵臂连接处的动态响应对这三个参数的灵敏度值，如表3所示。

表3 灵敏度值

根据扭力梁悬架的结构特点，这里设横梁厚度取值2≤th≤5 mm，调整横梁与纵臂连接点的位置前后移动20 mm，即lh-20≤ lh≤ lh+20 mm。由于路面激励与路面状况及车速等因素相关，比较复杂，在分析时保持路面激励不变，主要考虑发动机激励。在发动机经济转速2 800 r/min，Ω=93.33 Hz≈ω2的条件下对横梁与纵臂连接处进行动态响应分析。根据式（11）的动态性能优化设计模型，结合式（1）所示的动力学程，利用MATLAB进行仿真优化，可得优化前后设计参数的值，如表4所示。

表4 优化前后后扭力梁悬架系统设计变量值

优化前后横梁与纵臂连接处的动态响应仿真曲线如图2图3所示。对比图2图3可知，当发动机转速为2 800 r/min时，横梁与纵臂连接处的动态响应最大值由原来的11.5 mm下降到了7.2 mm，减少了37.3%。可见，在动态性能优化设计时充分考虑悬架动态性能与材料参数、结构参数、外激励参数的影响，能使优化设计的结果更合理，更符合实际情况。

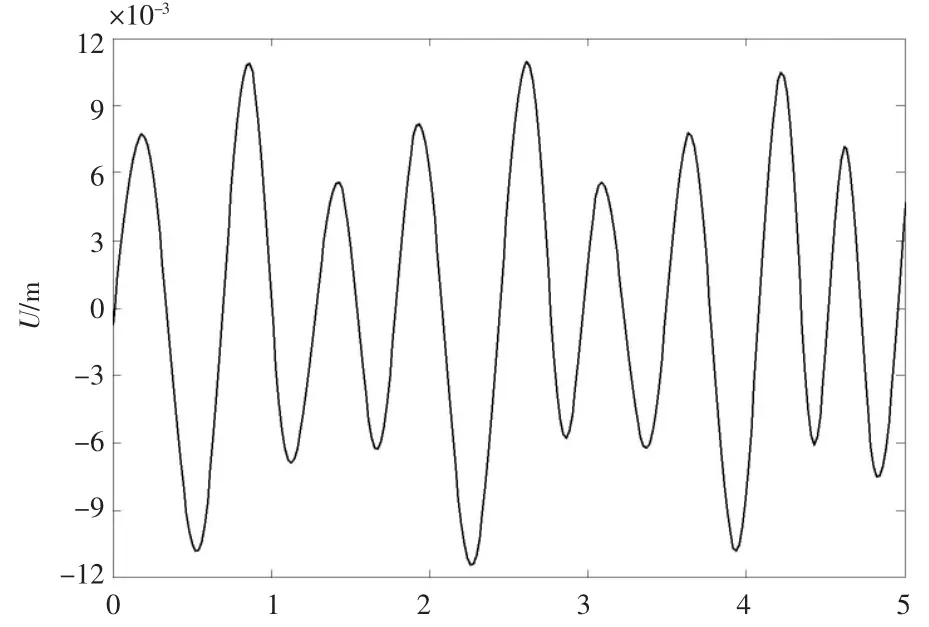
图2 优化前横梁与纵臂连接处的动态响应仿真曲线

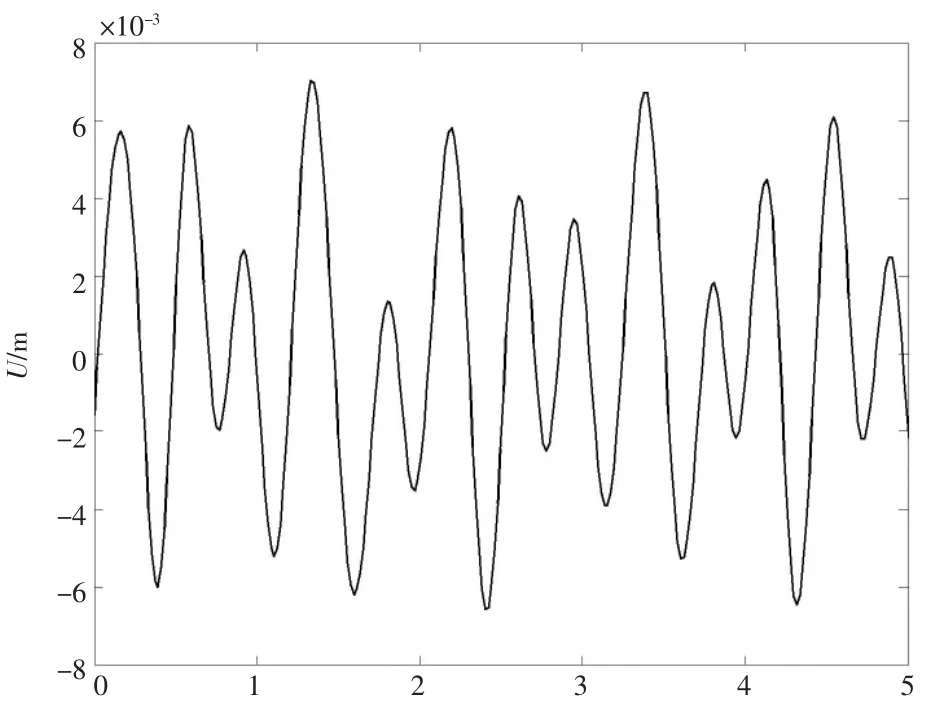
图3 优化后横梁与纵臂连接处的动态响应仿真曲线

5 结束语

本文在所建立的汽车后扭力梁悬架系统动力学方程基础上，以汽车后扭力梁悬架系统的结构参数为设计变量，横梁与纵臂连接处的动态响应峰值最小为目标函数，给定频率范围为约束条件，构建了汽车后扭力梁悬架系统优化模型，为汽车后扭力梁悬架系统动态性能的优化提供一种合理有效的方法。研究表明：

（1）前三阶固频率对横梁厚度的灵敏度比对纵臂厚度和横梁在纵臂的位置的灵敏度都要大，即前三阶固频率对横梁厚度的变化较敏感。

（2）横梁与纵臂连接处的动态响应对横梁与纵臂连接点的位置的灵敏度比对纵臂厚度和横梁厚度的灵敏度都要大，即横梁与纵臂连接处的动态响应对横梁与纵臂连接点的位置较敏感[1]。