无黏性有限土体主动破坏及土压力离散元分析

万励，张兴周，王宇峰，徐立明，徐长节，3

(1.浙江大学 滨海和城市岩土工程研究中心;浙江省城市地下空间开发工程技术研究中心，杭州 310058；2.浙江交工集团股份有限公司，杭州 310000；3.华东交通大学 土木建筑学院；江西省岩土工程基础设施安全与控制重点实验室，南昌 330013;4.浙江杭海城际铁路有限公司，浙江 嘉兴 314000)

随着城市建设的不断推进，建筑密度逐渐加大，临近既有建筑开挖深基坑的工程案例(如边坡挡土墙、临近地铁车站基坑工程等)也越来越多。这种情况下，基坑围护结构后方填土为有限宽度的情况也越来越普遍(图1)。目前，经典的朗肯及库伦土压力理论，均假定墙后填土为半无限体。而在此类工程中，由于临近建筑物的影响，墙后土体范围有限，而库伦或朗肯土压力理论滑裂面在贯穿土体表面之前先交于既有建筑外墙，因此，在这种情况下，用这一类经典土压力理论进行计算往往会使土压力计算结果偏大，造成安全系数偏小，设计偏保守。

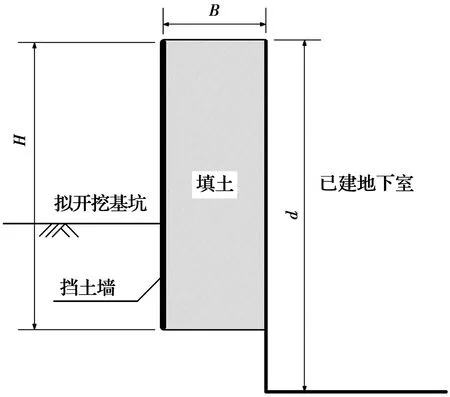
图1 邻近既有地下室的挡土墙Fig.1 Retaining wall adjacent to existing

由以上分析可知，目前针对墙后有限土体主动破坏模式的研究尚处于起步阶段。本文针对无黏性土(即土粒之间的粘结力很弱或无粘结，往往形成单粒结构的土体)，在前人的研究基础上，采用离散元数值分析软件PFC2D，对比研究墙体有、无摩擦情况下刚性挡墙平动过程中滑裂面的发展以及主动土压力的分布情况，探究墙后有限土体主动破坏模式。

1 离散元模型及参数

分析模型挡墙高1 m，采用圆形颗粒与刚性墙单元，模型如图2所示。左侧挡墙分为10段墙体单元，每段墙高0.1 m；右侧挡墙始终保持静止，模拟地下构筑物外墙。挡墙底部0.25 m部分模拟墙后填土底部垫层，在模拟过程中保持静止。通过变化墙后填土宽度，分别模拟有限至半无限状态的土体，即取墙后土体宽度与高度比值(宽高比)n=B/H=0.2、0.4、0.6、1.0进行模拟。其中，B为墙后填土宽度；H为墙后填土高度。

离散元模拟分为生成和加载两个阶段。

为得到合理的初始应力，生成阶段分两个步骤进行。第1步，采用Lai等[15]提出的改进多层压实法(IMCM)，分10层生成颗粒，颗粒初始参数取值见表1。颗粒级配为0.78～1.94 mm，中值粒径d50=1.36 mm。在生成阶段，颗粒与颗粒以及颗粒与墙体之间接触均保持光滑。初始颗粒生成后，在g=9.8 m/s2的重力场下固结平衡。第2步，将填土初始参数修改为表1中的模拟参数取值，并再次平衡。颗粒试验参数参考文献[15]。颗粒间的内摩擦角可通过建立数值双轴压缩试验获得。采用相同方法分别制备孔隙比e=0.176、0.219、0.282的试样，进行双轴压缩试验数值模拟。模拟结果如图3所示，得到残余应力比τ/σ=0.41，其中，τ=(σ1-σ3)/2，σ=(σ1+σ3)/2，σ1、σ3分别为大、小主应力。根据式(1)[15]得颗粒间内摩擦角约为24°。

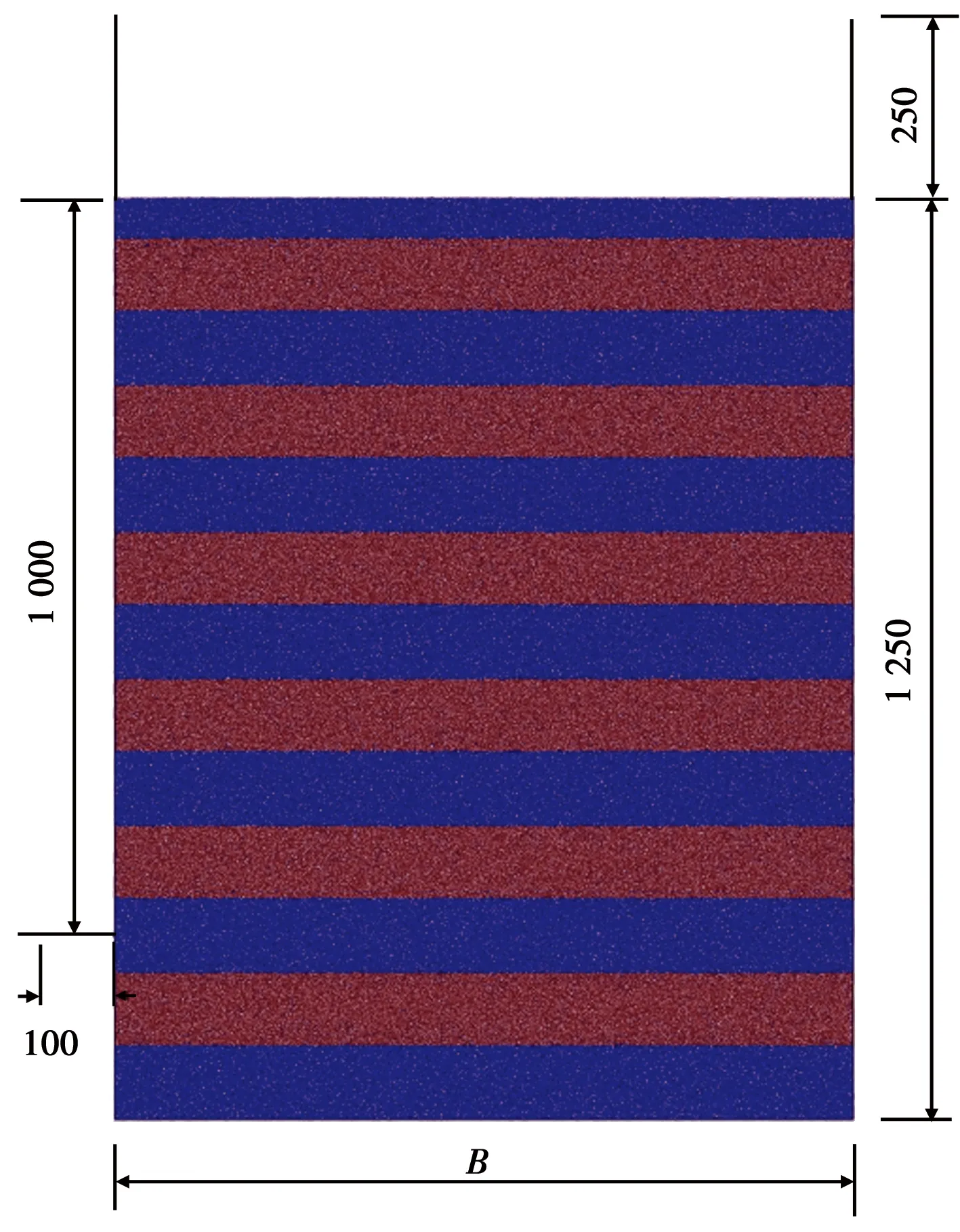
图2 墙后填土模型示意图Fig.2 Sketch of soil behind the retaining

(1)

表1 颗粒试验参数取值Table 1 Initial particle parameters used in DEM analysis

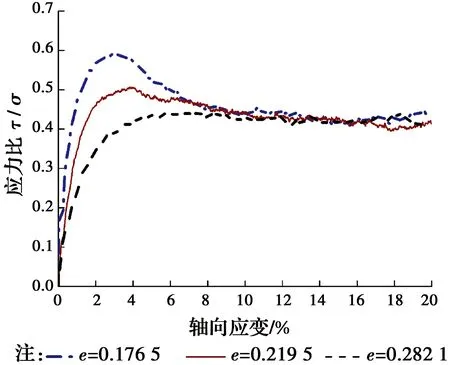
图3 应力比与轴向应变关系Fig.3 Relations between stress ratio and axial

用此生成方法所得初始水平土压力与理论水平土压力比较如图4所示。理论静止土压力采用公式σ=k0γh计算，式中k0=1-sinφ,φ为土体内摩擦角[17]。可见，模拟结果与理论计算结果基本吻合，土体初始应力状态合理，可对试样进行加载。

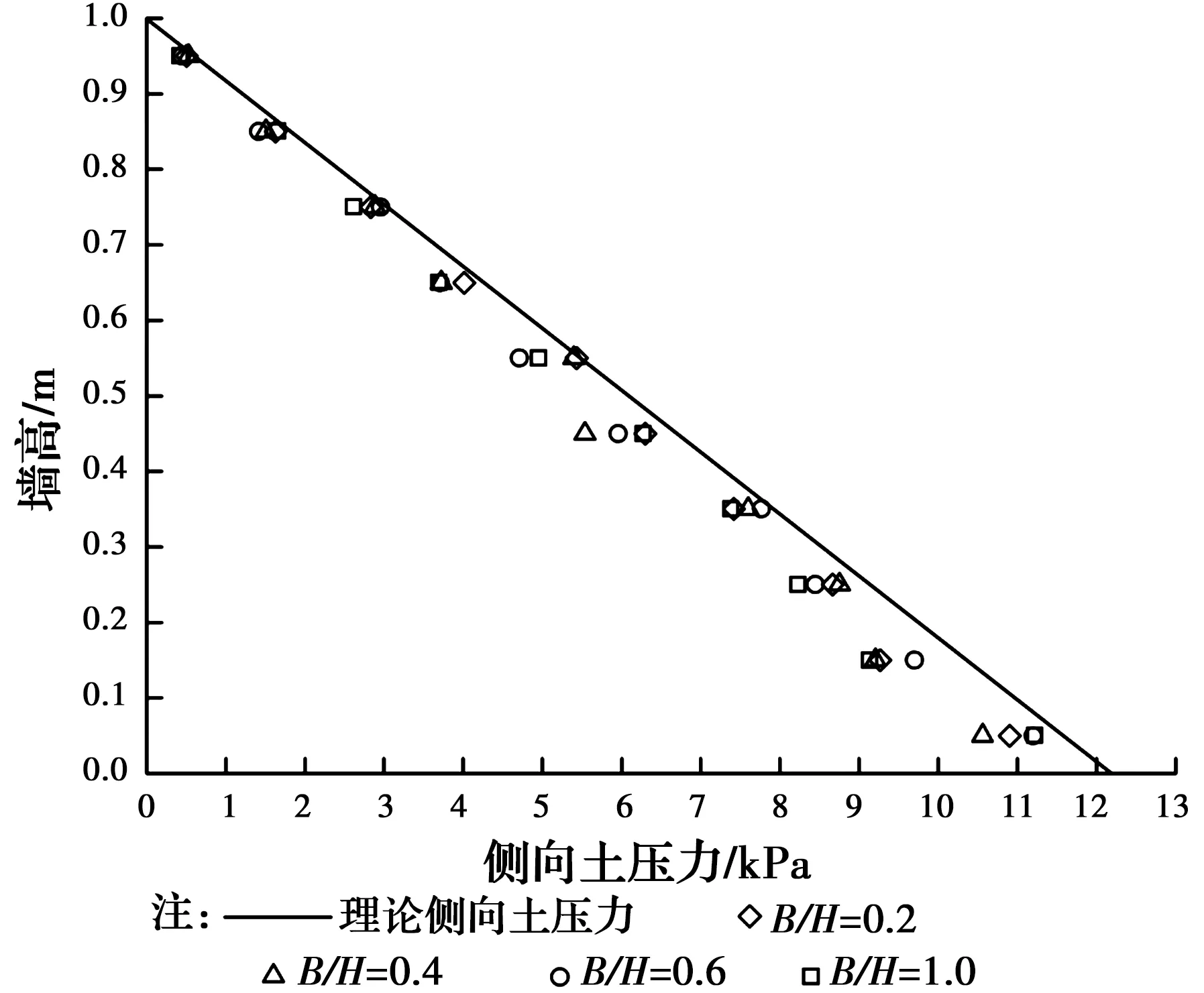
图4 理论静止土压力与模拟静止土压力Fig. 4 At-rest earth pressure from numerical simulations

加载阶段为保证墙后土体处于准静态模式，设置挡墙移动速度为1×10-3m/s。模拟过程中，对作用在每段挡墙上的土压力水平分量和竖直分量进行记录。当土压力合力随墙体位移变化量趋于稳定时，视土体达到极限状态。由于颗粒粗糙，在滑裂带出现的位置上，颗粒间的相对运动将使得颗粒发生转动，故滑裂带位置可用颗粒转角表示[18]。当墙土无摩擦，墙后填土宽高比n=2.0时(此时可视墙后土体为半无限情形[16])，数值模拟所得滑裂面近似为平面，其与水平面夹角基本与库伦理论滑裂面倾角(57°)相符，如图5。因半无限模型的颗粒间、颗粒与墙体间接触模型以及土体破坏机理与有限土体模型一致，故这一结果也证明了数值分析模型的可靠性。且由于离散元数值模拟直接对颗粒接触进行模拟，在不同应力水平下，也能保证结果的准确性，因此得出的结论也可推广使用。

图5 墙后填土颗粒转角示意图(S/H=2.5‰)Fig. 5 Sketch of slip surface in soil behind the retaining

2 墙后土体破坏分析

2.1 墙后土体宽高比影响

2.1.1 粗糙墙面 挡土墙后摩擦可通过设置不同的墙体摩擦系数μ来实现，以μ=0.7为例，墙面墙土摩擦角δ可通过式(2)获得[19]。

(2)

式中：Fy和Fx分别为作用在整段挡墙上土压力合力的竖直分量与水平分量。模拟过程中，通过对这两个分量的记录，可以得到不同宽高比情况下墙土摩擦角随挡墙位移的发展趋势，如图6所示。其中S为挡墙移动距离。当墙体位移超过1.2‰H时，墙土摩擦角达到稳定值，约为23°。

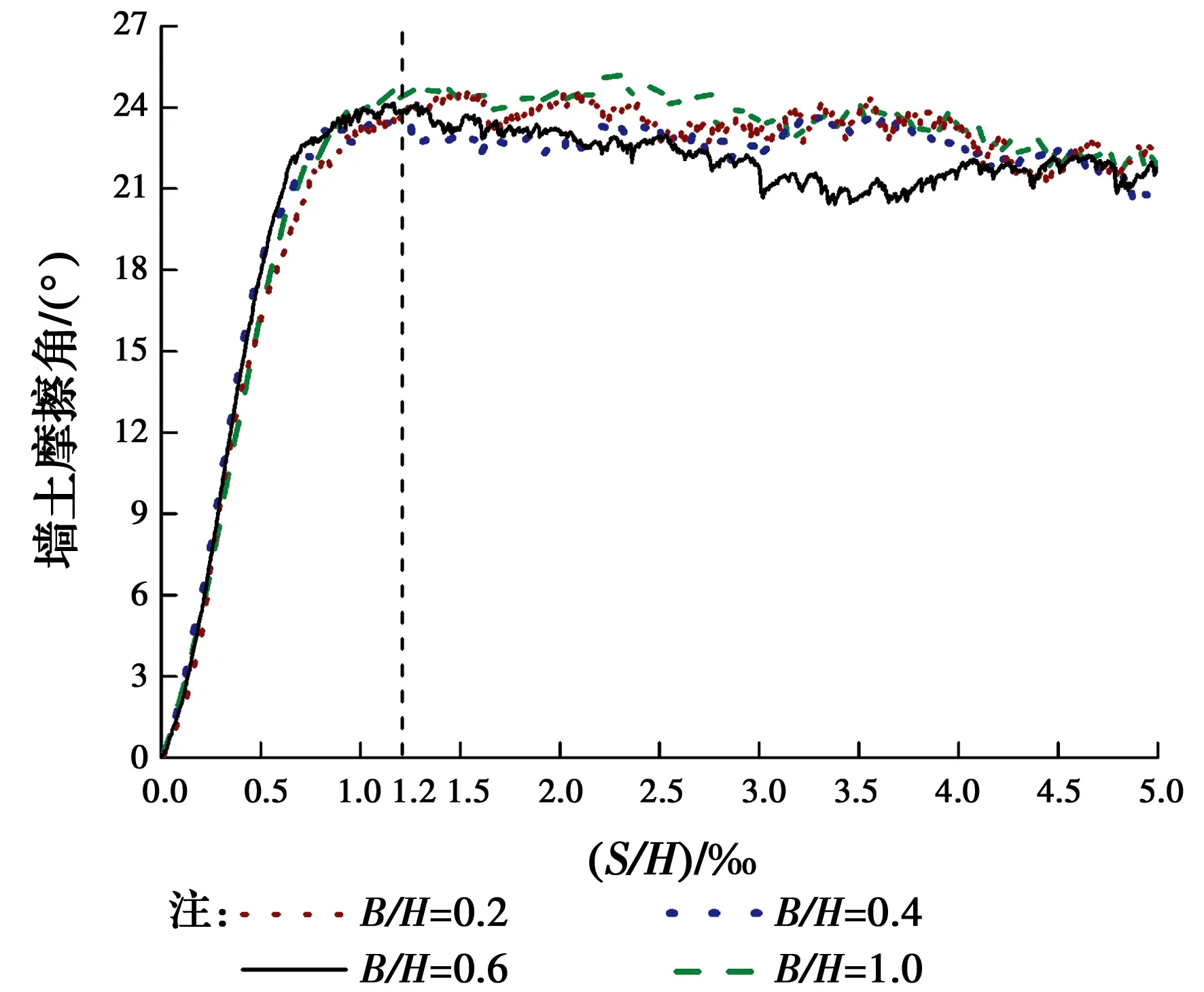
图6 墙土摩擦角随挡墙位移变化示意图(μ=0.7)Fig. 6 Mobilization of the soil-wall interface friction angle

图7为粗糙墙面不同宽高比下，墙体位移量与墙高之比S/H达到2.5×10-3时的土颗粒转角示意图(在本模拟中，墙体位移量与墙高之比S/H达到2.5×10-3时，所有算例土压力合力随墙体位移变化量趋于稳定，可视土体达到主动极限状态)。可见，当土体宽高比较大时(n=1.0)，达到极限状态后，墙后土体由从墙踵出发的一条直线滑裂带AB和一条曲线滑裂带AC分割。直线滑裂带AB发生于贴近墙体的土体之中，曲线滑裂带AC有一定宽度，远离墙踵一侧较宽。

图7 粗糙墙面墙后填土颗粒转角示意图(S/H=2.5‰, μ=0.7)Fig.7 Sketches of particle rotations in soil behind

当土体宽高比较小时(n=0.6、0.4、0.2)，土体破坏面主要由三段滑裂带BA、AD、DC组成。曲线滑裂带AD与右侧墙面交于点D，随后沿墙体DC直线延伸至土体表面，无法观察到明显的滑裂带反射现象。

随着土体宽高比的减小，曲线滑裂带AD的倾斜程度逐渐增大，墙踵处滑裂带AD的切线倾角稍小于墙体粗糙情况下库伦理论所得到的滑裂面倾角(51°)[8]。但随着滑裂带的发展，其切线倾角逐渐增大，且宽高比越小，增大越明显，最终滑裂带AD位于库伦理论滑裂带内侧(图7、图8中黑色实线)。此滑裂带形状与文献[4]模型试验结果基本一致。

2.1.2 光滑墙面 图8为光滑墙面不同宽高比下，墙后土体达到极限平衡状态下的颗粒转角示意图。当宽高比n=1时(图9(a))，随左侧挡墙的位移增大，墙后土体向挡墙方向移动。达到极限状态后，墙后土体出现两条从墙踵出发，直至贯穿土体表面的直线滑裂带。滑裂带AB发生在墙体和土颗粒的界面上，滑裂带AC位于土体内部，且有一定宽度，与水平面夹角约为57°，与库伦理论相一致。以滑裂带AC为界，上方土颗粒位移方向基本一致，下方土颗粒基本保持静止(图10(a))。

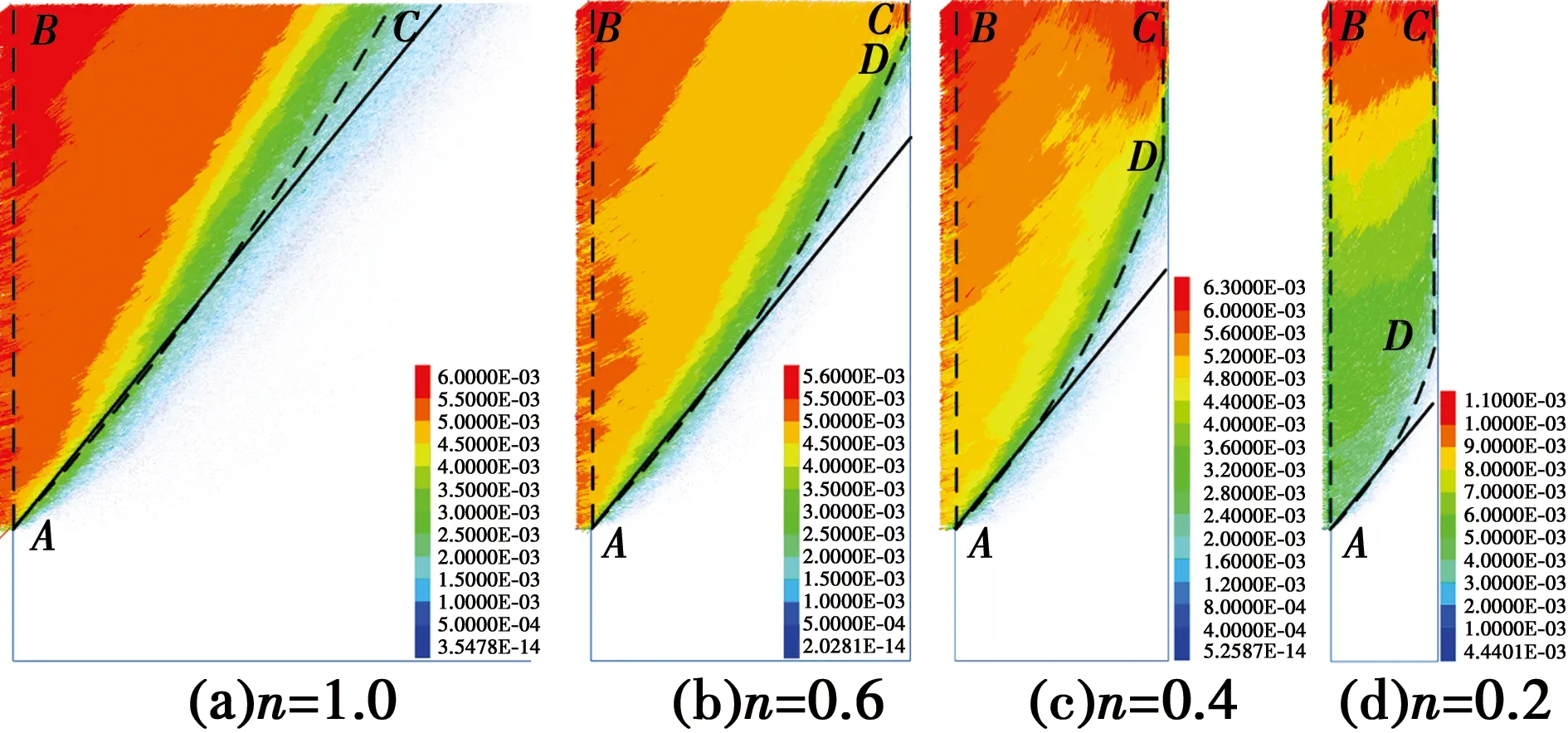
图8 粗糙墙面墙后填土颗粒极限平衡状态位移矢量场(S/H=2.5‰,μ=0.7)Fig.8 Displacement vector field of soil behind the rough wall under the ultimate equilibrium state(S/H=2.5‰)

随宽高比减小，滑裂带与水平面夹角基本不变(56°～59°)。与粗糙墙面不同的是，若一道滑裂带无法贯穿土体而是与另一侧墙面相交时，以相交点为起点，向左上方反射形成另一道滑裂带，至贯穿土体，如n=0.4(图9(c))，滑裂带AD上方土体被反射滑裂带DE划分成两块滑动土体。如图11所示，ADEB块体中颗粒向挡墙方向运动；DCE块体中颗粒竖直向下运动；滑裂带AD下方土颗粒基本静止不动。同一滑动土楔体中颗粒速度大小相近，运动方向一致，可近似将其视为刚体。不同滑块交界处颗粒运动方向不同，且颗粒间存在摩阻，导致交界面处颗粒搓动，产生转动，形成滑裂带。

若宽高比继续减小，如n=0.2(图9(d))，滑裂面反射一次后仍不能贯穿土体，则在E点发生二次反射，以此类推。

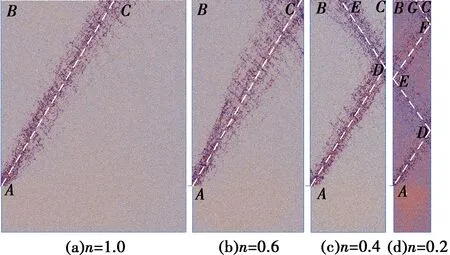
图9 光滑墙面墙后填土颗粒转角示意图(S/H=2.5‰)Fig.9 Sketches of particle rotations in soil behind the smooth

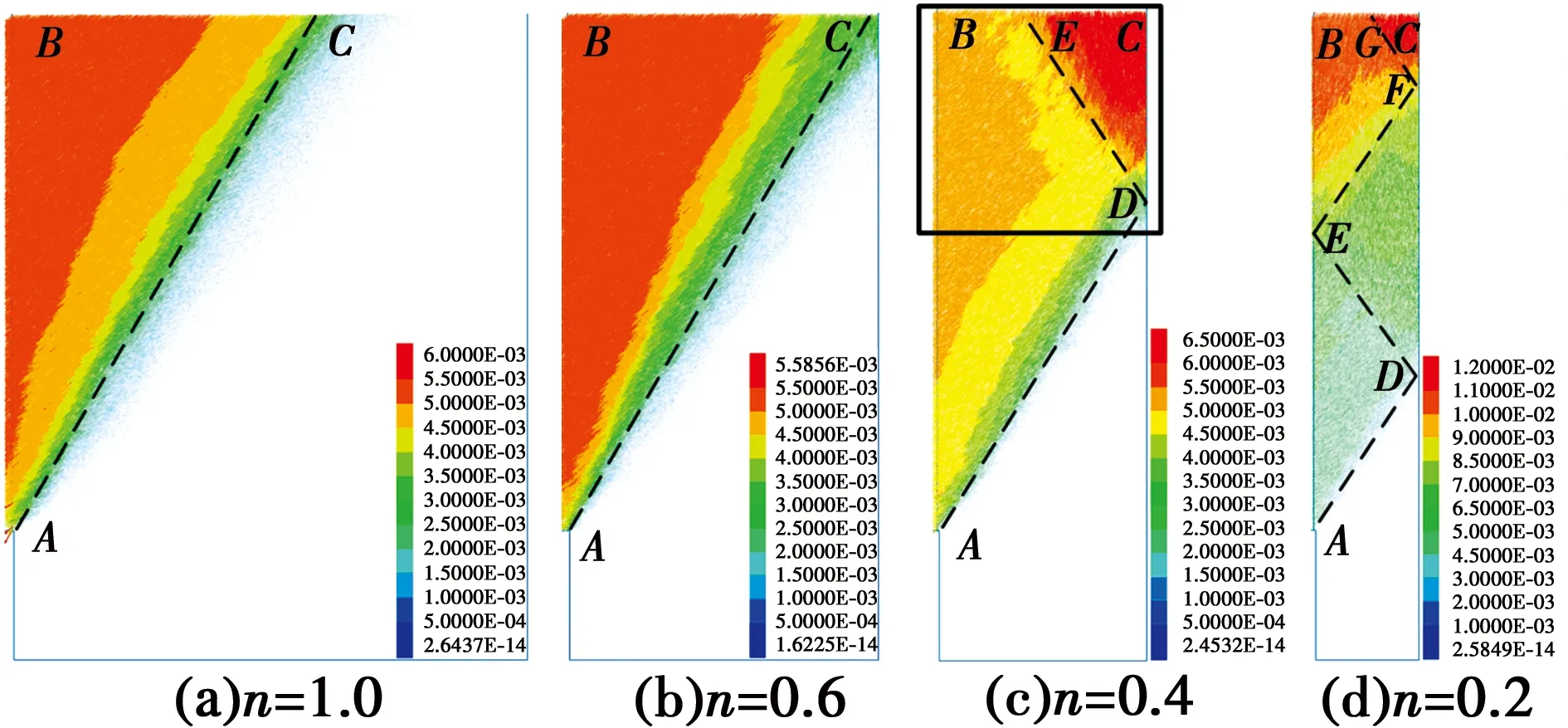
图10 光滑墙面墙后填土颗粒极限平衡状态位移矢量场(S/H=2.5‰)Fig.10 Displacement vector field of soil behind the smooth wall under the ultimate equilibrium state(S/H =2.5‰)

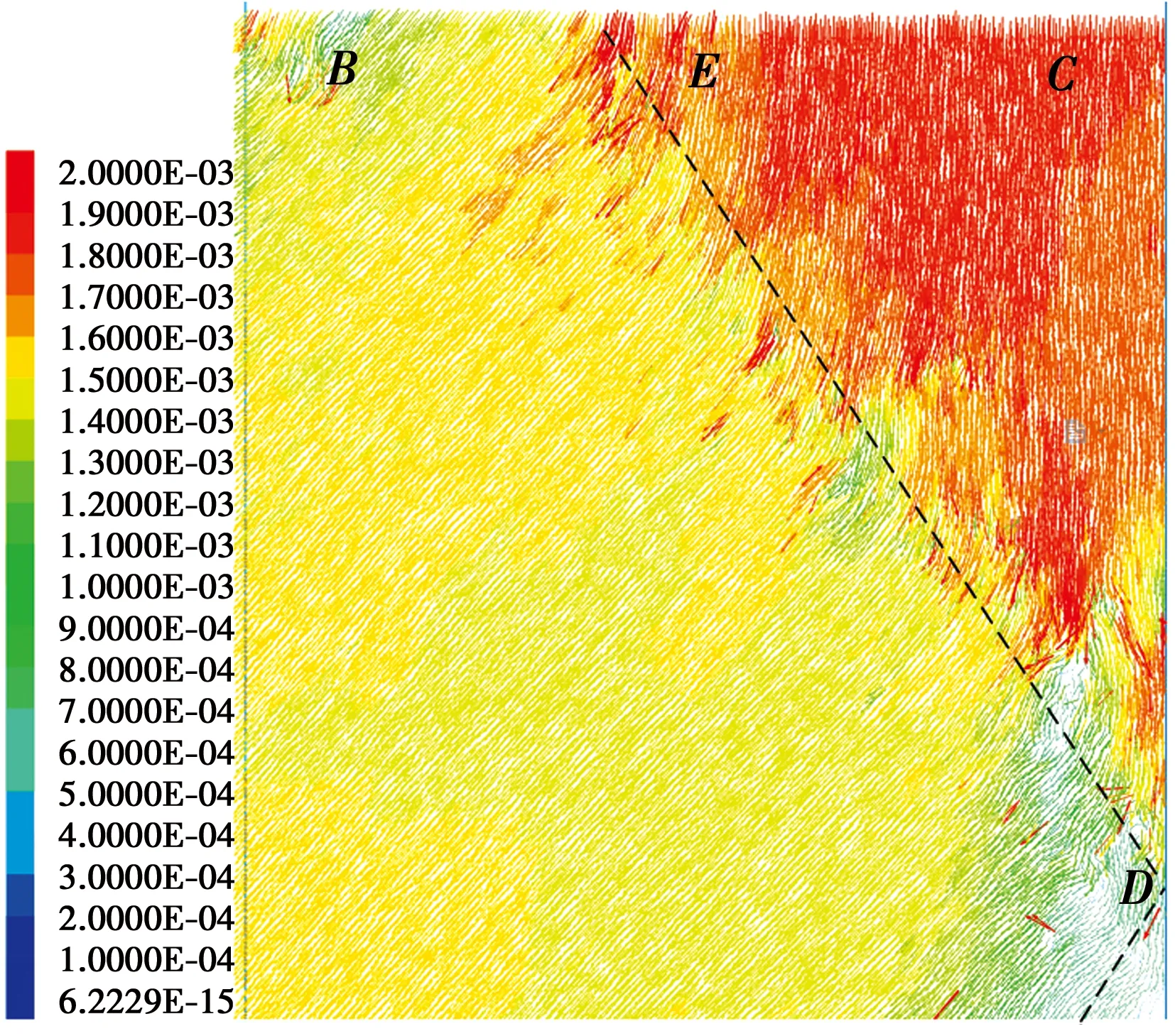
图11 局部瞬时速度矢量场(n=0.4)Fig.11 Partial transient velocity vector field

由以上分析可见，当墙土间存在摩擦时，土颗粒与移动墙体间的滑裂带发生在靠近墙体表面并与其接触的土颗粒之中。此时，贴近墙体的土颗粒运动将受到墙体的影响，发生转动，故无法简单地将包含这些发生转动颗粒的土楔体ABCD整体视为刚体进行分析。而墙体光滑的情况下，墙体对与其接触的土颗粒的运动无任何切向约束，土颗粒与墙体之间的滑裂面正好发生在墙土界面上，土楔体ABCD中靠近墙体的部分土颗粒将不发生转动。但此时若假设滑动土楔体ABCD为刚体，且不存在反射滑裂带DE，则随墙体位移的增大，滑动土楔体ABCD(图9(c))将与右侧墙体分离，右墙面上端将不受土压力作用。为保证在墙后土体有限的情况下土体不与右侧墙体分离，则必然推导出反射滑裂面DE的存在[10]。此破坏模式在理论分析中并不少见，然而，室内试验中墙体摩擦不可忽略，难以模拟出光滑墙面，因此，试验无法观察到多折线破坏模式，得出的滑裂带通常为弧线[4-5]。

2.2 墙土摩擦角影响

由以上分析可知，墙面是否粗糙对墙后土体破坏模式影响显著。为探究墙面粗糙程度对模拟结果的影响，以反射现象最为明显的一组宽高比(n=0.4)为例，分别改变墙土摩擦系数μ=0、0.3、0.5、0.7进行模拟，所得墙土摩擦角分别为：0°、15°、20°、23°(图12)。

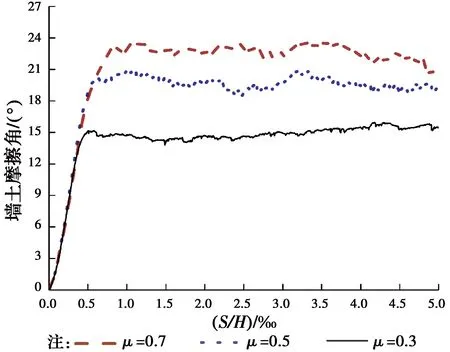
图12 墙土摩擦角随墙土摩擦系数变化示意图(n=0.4)Fig.12 Sketches of soil-wall friction angles vary with soil-wall

不同墙土摩擦系数所得出的墙后有限土体破坏模式如图13所示。随墙土摩擦系数增大，滑动土楔体内部更加破碎，滑裂带AD由直线变为曲线，反射滑裂带DE越不明显，即滑裂带反射现象随墙土摩擦系数增加而减弱。目前，不少解析解均基于墙后土体多道滑裂面的假定进行[10-11]，本文研究结果表明，只有当墙土摩擦角较小时，才可采取此假定。

图13 墙后土颗粒转角随墙土摩擦角变化示意图(S/H=2.5‰)Fig.13 Sketches of particle rotations of soil behind retaining walls vary with soil-wall friction angle (S/H=2.5‰)

3 土压力结果分析

在离散元数值模拟中，墙体位移量与墙高之比S/H达到2.5×10-3时，所有算例中，土压力合力随墙体位移变化量趋于稳定，可视土体达到主动极限状态。图14为不同宽高比下，土压力沿挡墙的分布规律随位移变化(S/H)示意图。

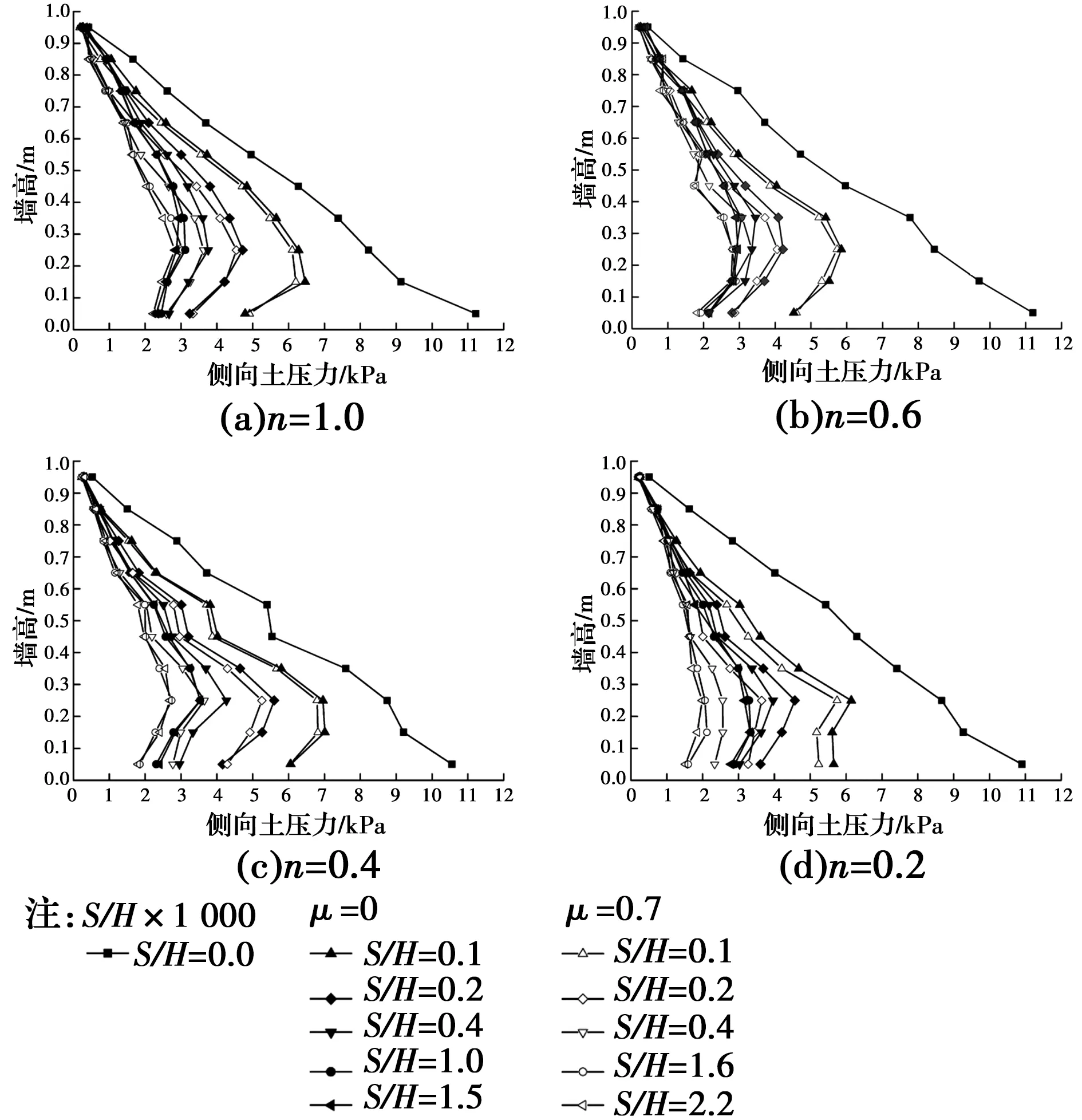
图14 挡土墙主动土压力分布图Fig.14 Distribution of active earth pressure along the depth of the

可见，随墙体位移增大，挡土墙上主动土压力逐渐减小，由于土拱效应的影响，土压力在墙踵附近减小较快。不论墙体是否有摩擦，土压力变化趋势基本相同。但挡墙粗糙情况下，土压力减小更快，达到极限状态时的土压力较小，且减小程度随宽高比n的减小而增大。

图15、图16分别是光滑墙体和粗糙墙体各级位移下，不同宽高比土体主动土压力合力随墙体位移的变化情况。可见，当墙体光滑时，不同宽高比对极限状态下主动土压力合力值的影响不大，但达到极限状态所需的位移随宽高比增大而增大。其中n=1.0时，S/H=1.0×10-3；n=0.2时，S/H=0.5×10-3。

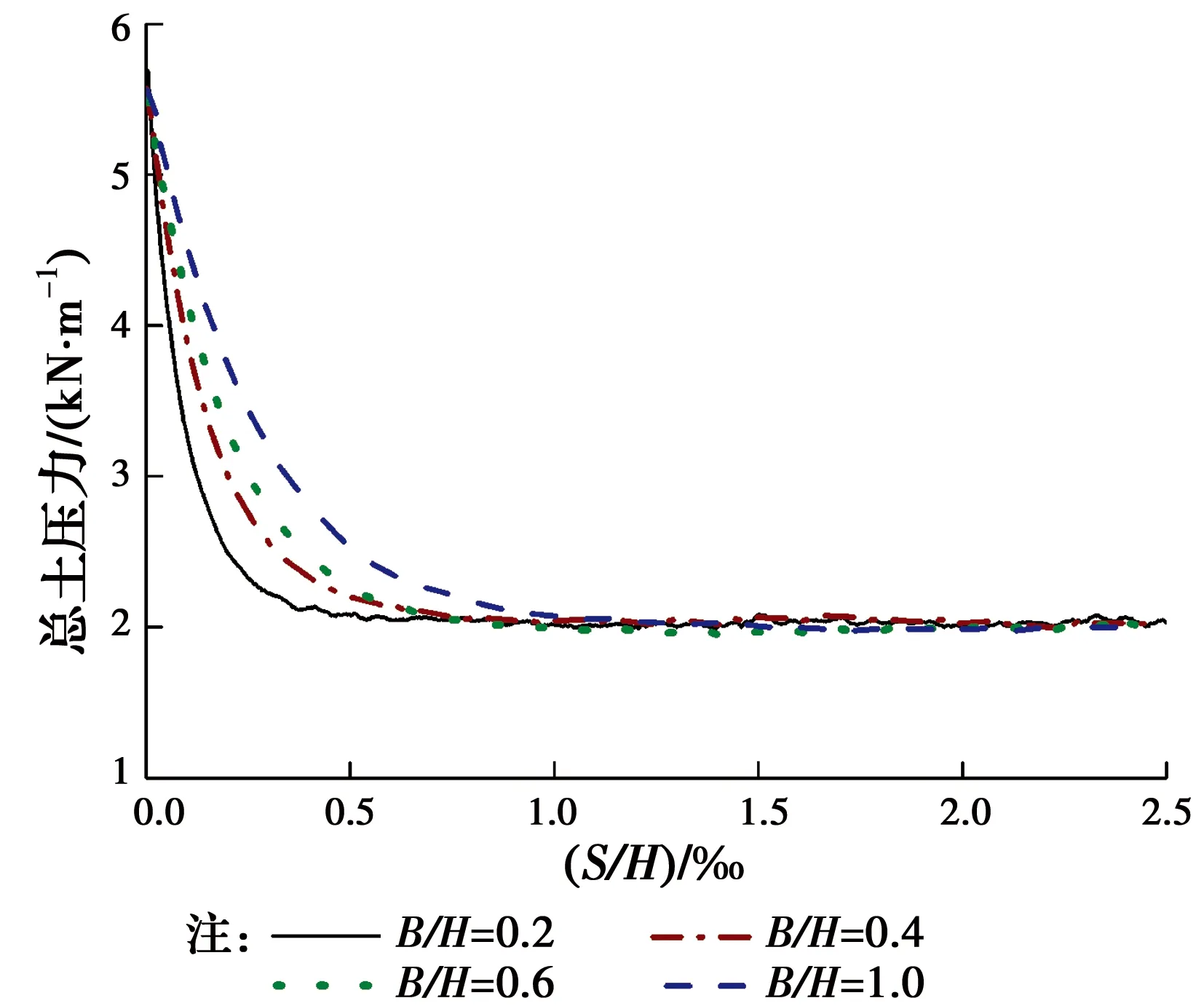
图15 光滑墙体墙后总土压力随位移变化曲线Fig.15 Total earth pressure against the smooth wall with

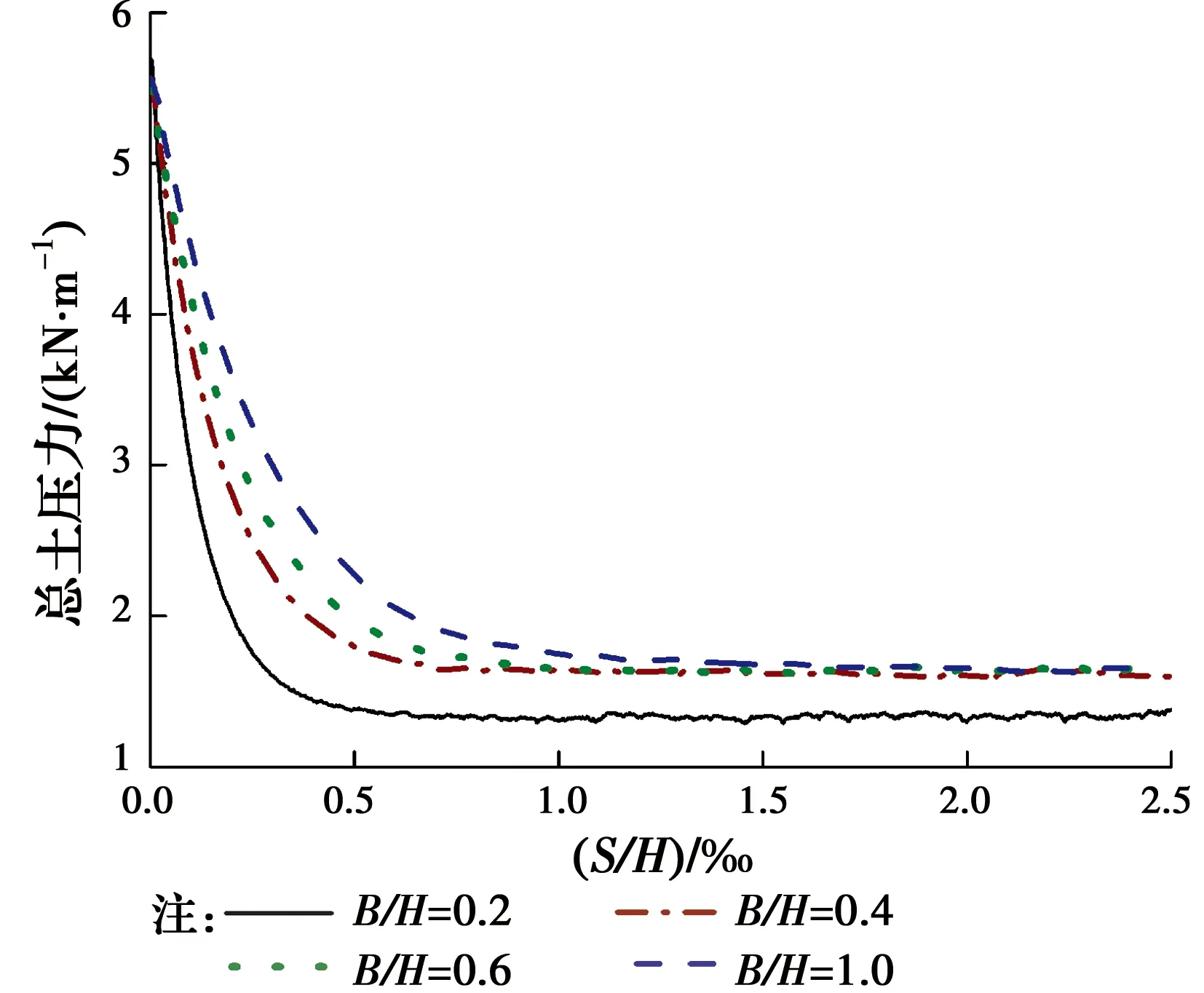
图16 粗糙墙体墙后总土压力随位移变化曲线(μ=0.7)Fig.16 Total earth pressure against the rough wall

当墙体粗糙时，主动土压力合力随宽高比增大而增大；墙后土体宽高比n≥0.4时，主动土压力合力受宽高比影响不大，但其值始终小于光滑墙面土压力。墙体粗糙情况下墙后土体达到极限状态所需的墙体位移稍大于光滑墙面，当n=1.0时，S/H=1.5×10-3；n=0.2时，S/H=0.6×10-3。

4 结论

采用离散元数值分析方法，对平动模式下的墙后有限宽度无黏性土体主动土压力问题进行了模拟，探讨了墙面粗糙及光滑两种情况下，不同土体宽高比及墙土摩擦角对土压力分布、土体破坏模式的影响，根据研究所得的结论可推导出适用于墙后土体有限情况下的土压力计算公式，更准确地指导类似工程的挡墙设计。

1)光滑墙面墙后土体主动破坏时，滑裂带为通过墙踵并贯穿土体的一道或反射成的多道直线。滑裂带将土体分割成多块滑动土楔体，土楔体中颗粒运动模式相似。滑裂带倾角与库伦理论解一致，且与墙后土体宽高比无关。

2)粗糙墙面墙后土体主动破坏的滑裂带为曲线，滑裂带与墙面相交后沿墙面贯穿土体表面，墙体越粗糙，滑裂带反射现象越不明显。位于墙踵处滑裂带的切线倾角稍小于库伦倾角，但随滑裂面的发展，其切线倾角增长较快，最终落于库伦理论破坏线内侧。

3)光滑墙面情况下墙后土体达到极限状态所需的位移较小，土压力减小速度较慢，达到极限状态的土压力大于粗糙墙面情况下的土压力，且土压力合力大小与宽高比无关。

4)粗糙墙面情况下，墙后土体达到极限状态所需的位移较大，土压力减小速度较快，且宽高比越小减小的程度越大。存在一临界土体宽高比，当土体宽高比小于此值时，主动土压力合力随宽高比增大而增大，而当土体宽高比大于此值时，主动土压力合力不再发生变化，墙后土体可视为半无限体。