非线性比例边界有限元在面板坝分析中的应用

邹德高，陈楷，刘锁，周扬

(1.大连理工大学 水利工程学院；海岸和近海工程国家重点实验室，辽宁 大连 116024；2.中国电建集团 华东勘测设计研究院有限公司，杭州 311122)

面板堆石坝由于可就地取材、经济、抗震性强等优点，一度成为坝工界青睐的首选坝型[1]，但其结构尺寸相差悬殊，面板最小厚度仅为0.3 m，与坝体整体尺寸差别数百倍至千倍之多。面板作为大坝最重要的结构，应力梯度高，应布置较密的网格[2]，且实际研究[3-4]表明，精细的网格密度将获得更合理的模拟结果。

有限单元法使用简便、通用性强、工程应用广[5]，是面板坝等岩土工程结构安全评价的有效技术手段，但该方法单元形式单一，平面网格严格限制为三角形和四边形单元，网格离散限制多，对复杂边界适应性较差[6]。尤其在尺度跨越大的面板坝工程精细化分析中，需消耗大量时间进行较为繁琐的人机交互前处理，一定程度上降低了自动化程度和分析效率[7-8]。近年来，Wolf等[9]提出了弹性的比例边界多边形有限元(scaled boundary polygon finite element method, SBPFEM)，该方法更加灵活自由，融合了边界元(boundary element method, BEM)和有限元法(finite element method, FEM)的优点，并规避了两者的不足，且已被证明精度和收敛性都高于多边形有限元的数值算法[10]，被学者们应用到多个领域：如电磁问题分析[11]、土与结构相互作用分析[12]、裂纹扩展分析[13-14]、面板动水压力研究[15-16]、三维复杂多面体应用[17-18]、波的传播问题分析[19]等。此外，为探索SBPFEM的非线性应用，Chen等[20]利用半解析的弹性解构造单元形函数，采用两套高斯点方案，实现了比例边界多边形有限元的非线性分析，并将其拓展于多孔介质动力液化分析[21]及三维弹塑性岩土工程应用[22-24]。

采用笔者自主开发的非线性比例边界多边形单元，对典型面板堆石坝进行了系统的静力、动力和永久变形分析计算，并与传统有限单元法对比，以验证提出的方法在面板坝工程分析中的可靠性和合理性。随后，与高效的四分树离散技术无缝耦合，进行面板坝结构快速跨尺度精细化分析应用，以揭示SBPFEM能在面板坝工程精细化分析中脱颖而出的显著优势。

1 工程应用探究

计算程序采用作者完全自主研发的大型岩土工程非线性分析软件平台GEODYNA[25]，非线性比例边界多边形单元被集成到该平台。

1.1 理论概要

比例边界有限元是一种弹性的半解析数值方法，其环向离散、径向解析的特点使其可降低一个计算维度，减少一定的计算量。对任意问题域，可用任意n边形对求解域离散(n> 2)，如图1所示。通过对每个子域进行求解可获得整个求解域的数值结果。理论详尽推导，可参见文献[9-10,20]。

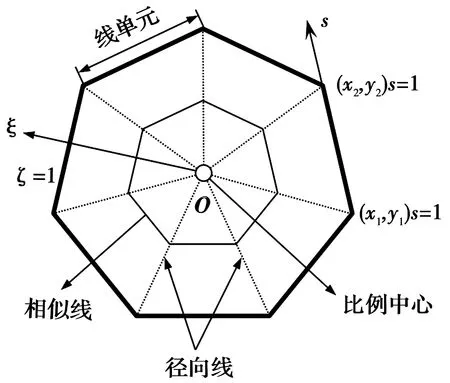
图1 比例边界多边形有限单元Fig.1 Scaled boundary polygon finite

弹性框架限制了该方法的应用领域，本着拓展推广SBFEM的原则，采用非线性化的比例边界多边形单元。采用两套高斯点策略：保留原始的边界线高斯点，用于计算相关系数矩阵和半解析的弹性形函数；同时，引入内部高斯积分点，可积分获得考虑了材料非线性的单元刚度矩阵，进而组装得到计算域的总体刚度矩阵，并采用Newton-Raphson迭代算法用于求解非线性平衡方程，从而实现该方法的非线性分析。开发的单元可以求解常规单元及传统常规有限元无法计算的多边形单元(常规凸多边形和四分树单元)，见图2。详细理论推导和计算可参考文献[9,20,26-29]。

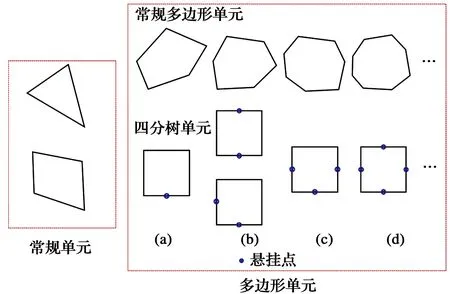
图2 比例边界有限元支持单元类型Fig.2 Supported element types in

1.2 程序验证

采用弹性悬臂梁结构端部受弯分析验证实现程序的正确性和计算精度，结构尺寸及网格如图3所示，其中l=1.2 m、h=0.4 m、弹性模量E=3×1010、泊松比v=0.2、荷载F=2.4×107N。

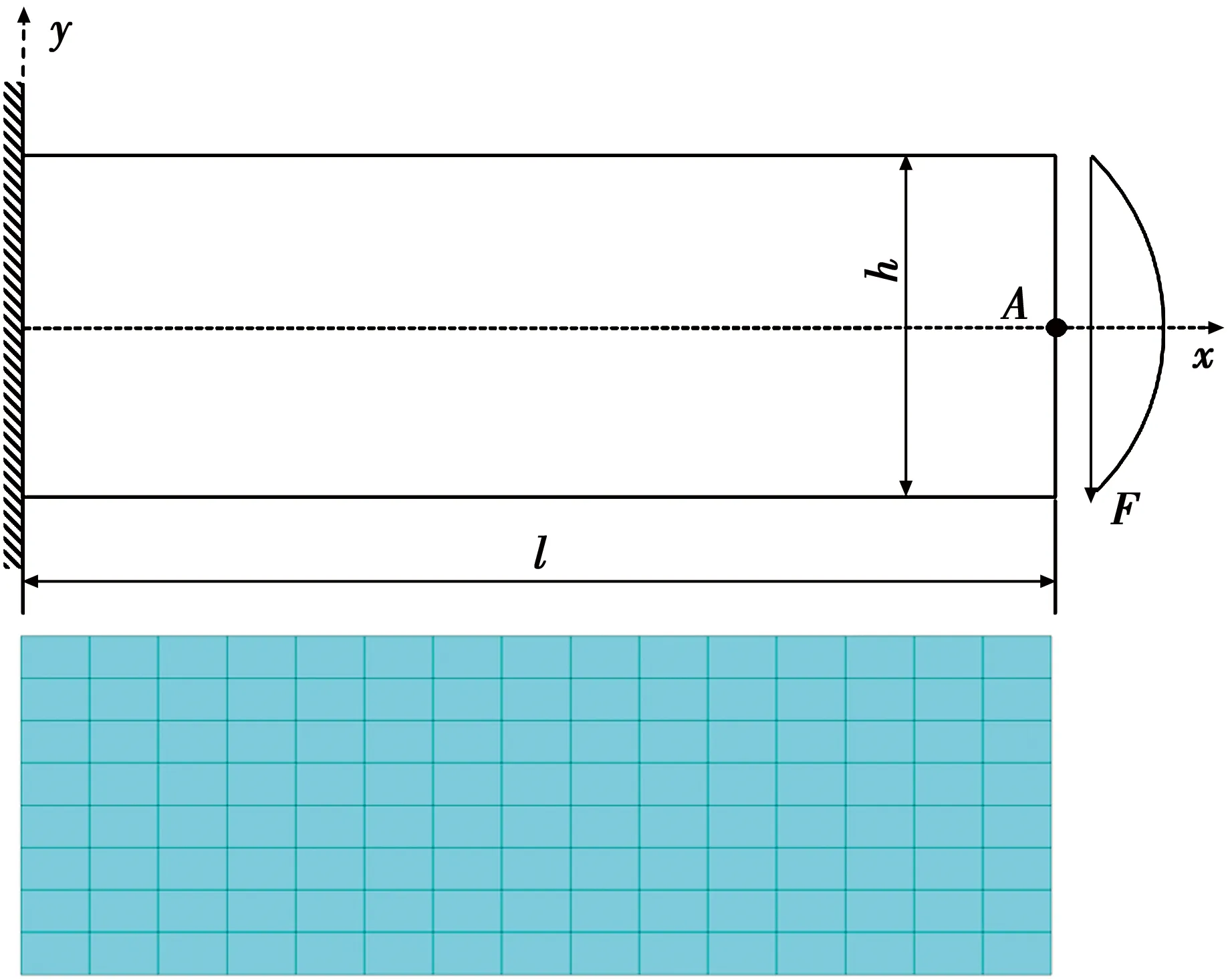
图3 悬臂梁结构及网格Fig.3 Cantilever structure and

采用SBPFEM和FEM分别计算相同结构，并与理论近似解(采用文献[20]提供的公式)进行对比，分析结果列于表1。从表1可以看出，采用的SBPFEM具有更高的精度。

表1 计算结果与理论解比较Table 1 Comparison between calculation results and theoretical approximate solutions

1.3 工程算例验证

以典型面板堆石坝为例，坝高为155 m，坝顶宽度为17 m，面板坡比1∶1.8，主体结构材料分区包括面板、垫层区以及堆石料区。为更合理地模拟面板变形和应力，面板与垫层之间添加无厚度的Goodman接触面单元，面板与趾板之间添加缝单元。常规有限元网格离散单元个数为1 702，节点个数1 816，分析模型见图4。

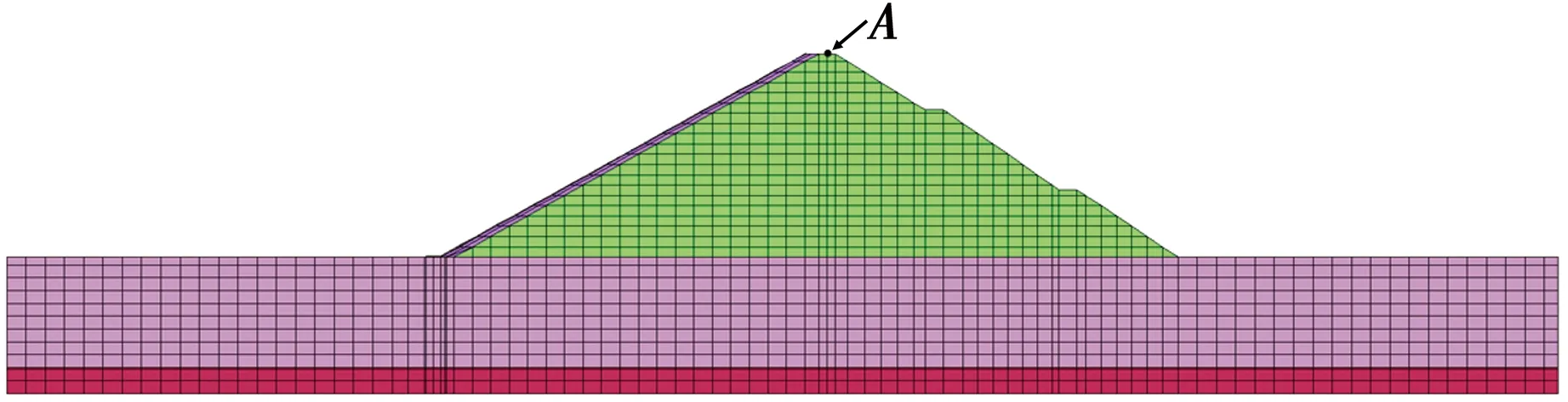
图4 面板坝有限元网格Fig.4 Mesh of concrete face rock-fill

1.4 材料参数

静、动力均采用堆石料广义塑性模型[30]模拟筑坝材料变形特性，参数列于表2。面板与垫层间设置的接触面采用广义塑性接触面本构模型[31]，详细参数见表3。

表2 筑坝材料广义塑性模型参数Table 2 Generalized plastic model parameters of dam material in static analysis

表3 广义塑性接触面参数Table 3 Parameters of the generalized plastic interface model

面板、趾板及基岩采用线弹性模型，参数见表4。缝单元参数采用文献[32]建议值，其法向压缩刚度为25 GPa/m，法向拉伸刚度为5 MPa/m，切向刚度为1 MPa/m。静力计算考虑了坝体的施工填筑和蓄水过程，坝体填筑分22个荷载步完成，随后分30个荷载步蓄水至152 m高程。

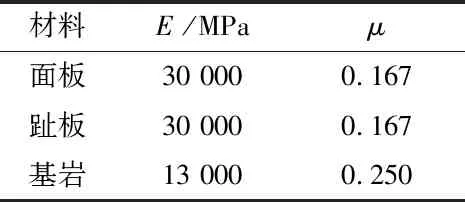
表4 线弹性材料参数Table 4 Parameters of linear model for concrete

1.5 地震动输入和计算方案

1.5.1 地震动输入 地震动输入采用规范谱人工波，顺河向峰值加速度为0.2g，竖向峰值加速度为顺河向的2/3。地震波加速度时程见图5。地震波持续时长为25.00 s，计算时间步间隔Δt取0.02 s。

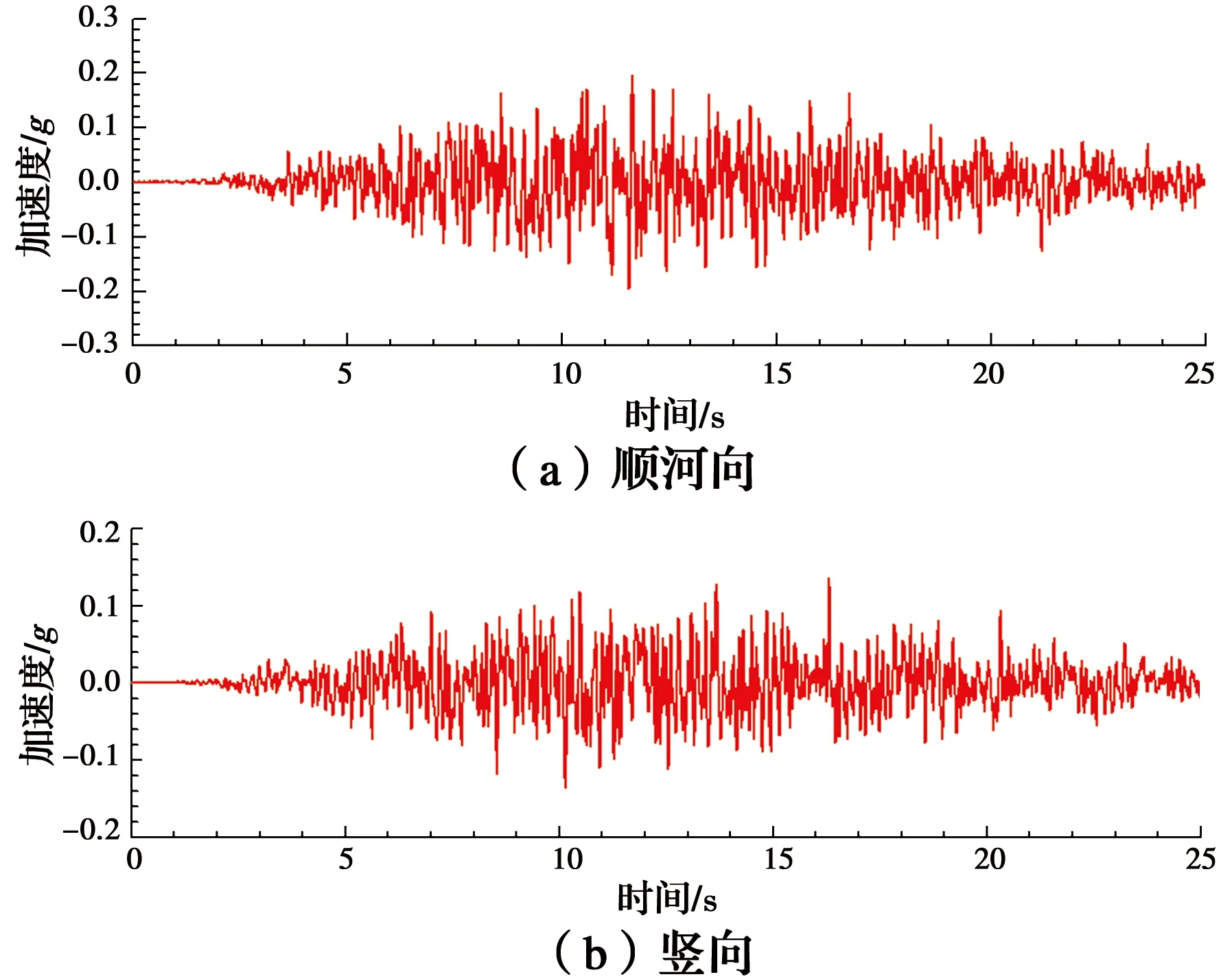
图5 地震波加速度时程曲线Fig.5 Time history curve of seismic wave

1.6 计算结果及分析

1.6.1 静力结果 图6为满蓄期的坝体位移等值线分布图。从图6可以看出，FEM计算结果与NSBPFEM结果吻合较好。图7为满蓄期面板应力变形，FEM与NSBPFEM结果基本一致。

表5给出了满蓄时坝体和面板应力变形的极值。从表5可见，两种方法计算结果相差较小，证明NSBPEM在模拟大坝填筑蓄水过程中的精度可以得到保证。

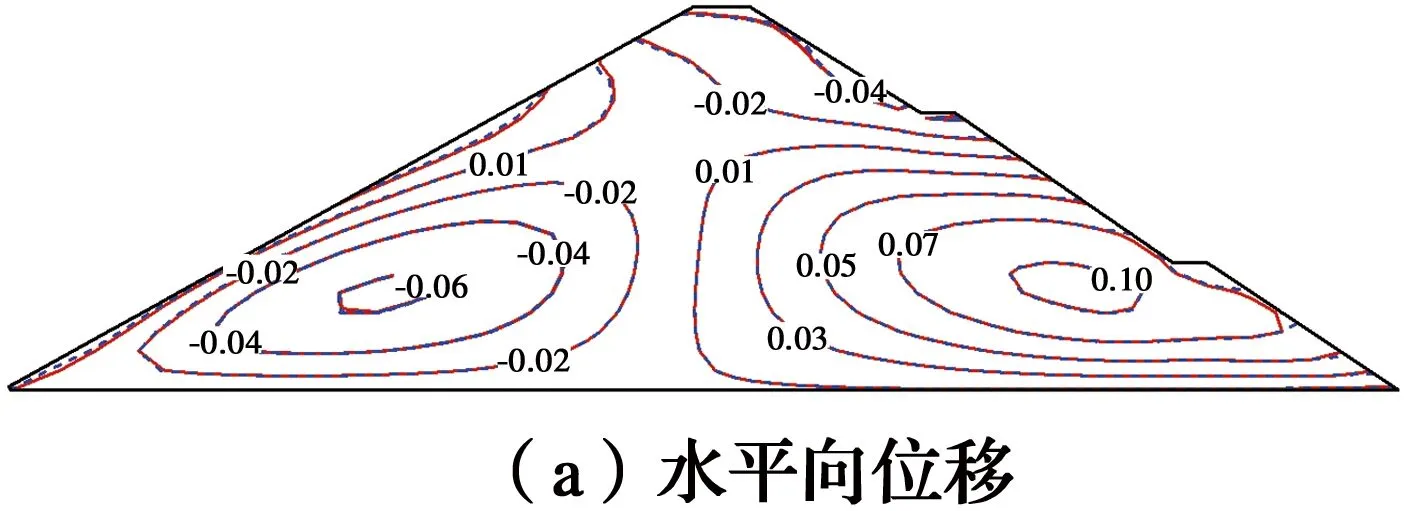
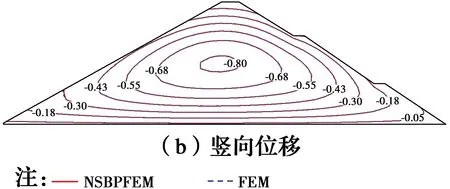
图6 满蓄期坝体位移(单位：m)Fig.6 Displacement of the dam after impoundment

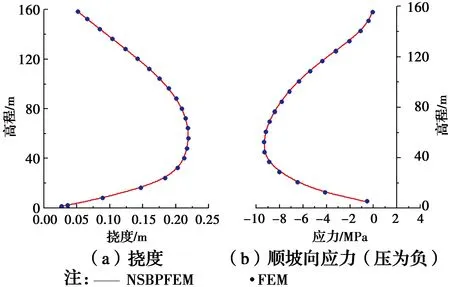
图7 满蓄期面板应力变形Fig.7 Deflection and stress along slope direction of face

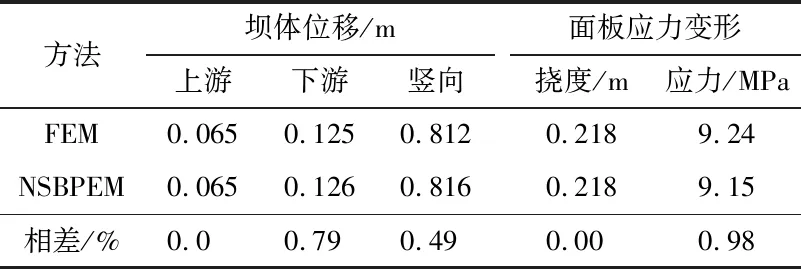
方法坝体位移/m上游下游竖向面板应力变形挠度/m应力/MPaFEM0.0650.1250.8120.2189.24NSBPEM0.0650.1260.8160.2189.15相差/%0.0000.7900.4900.0000.98

1.6.2 动力结果 图8为地震过程中面板顺坡向应力随高程分布规律。FEM计算应力与NSBPFEM计算结果非常接近。

表6列出了两种方法动力计算中坝顶A点的加速度的极值情况，结果显示两者相差不大，说明了NSBPFEM在动力计算中的可靠性。

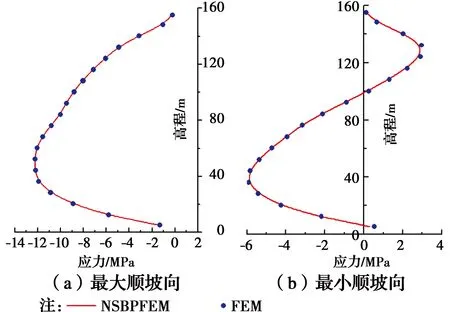
图8 地震作用下面板应力(压为负)Fig.8 Stress along slope direction of concrete face during

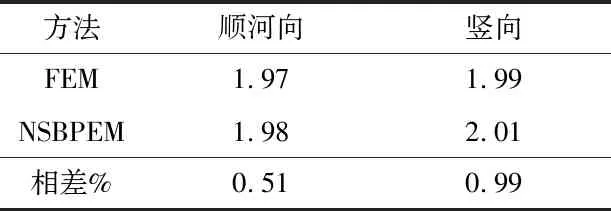
方法顺河向竖向FEM1.971.99NSBPEM1.982.01相差%0.510.99

1.6.3 永久变形结果 图9为地震后坝体永久变形计算结果。从图9可以看出，两者变形轮廓基本完全一致，说明NSBPFEM可用于震后永久变形计算分析。

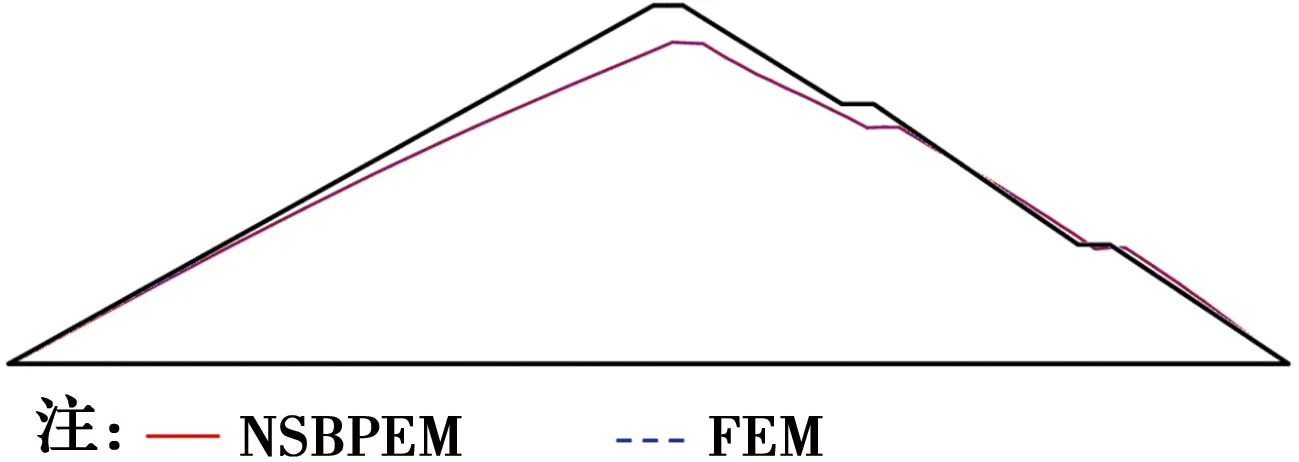
图9 堆石体震后永久变形(放大10倍)Fig.9 Permanent deformation of the dam body after

2 高效的跨尺度精细化分析

除可用于常规单元(三角形和四边形)分析外，SBPFEM的优势在于其可与传统有限单元不能直接处理的四分树网格离散技术无缝结合，进行高效的跨尺度精细化分析。四分树可快速实现尺度跨越，从1 m级到1 mm级仅需10层递归划分(210= 1 024)[33]。可自动进行高质量单元离散，且划分网格以正方形为主，仅边界和过渡区为多节点单元。

2.1 计算模型与参数

采用四分树技术，并结合SBPFEM对面板坝进行高效跨尺度精细化分析应用，其中，面板单元尺寸设定为0.5 m，坝体单元大小为8.0 m。如图10～图11所示，整个模型剖分时间仅为0.216 s。该技术可高效地实现跨尺度精细化分析，避免了文献[7-8]的不足。值得注意的是，该方法进行网格二次划分时，仅需重新定义最大和最小网格尺寸即可，显著改善了网格离散效率。

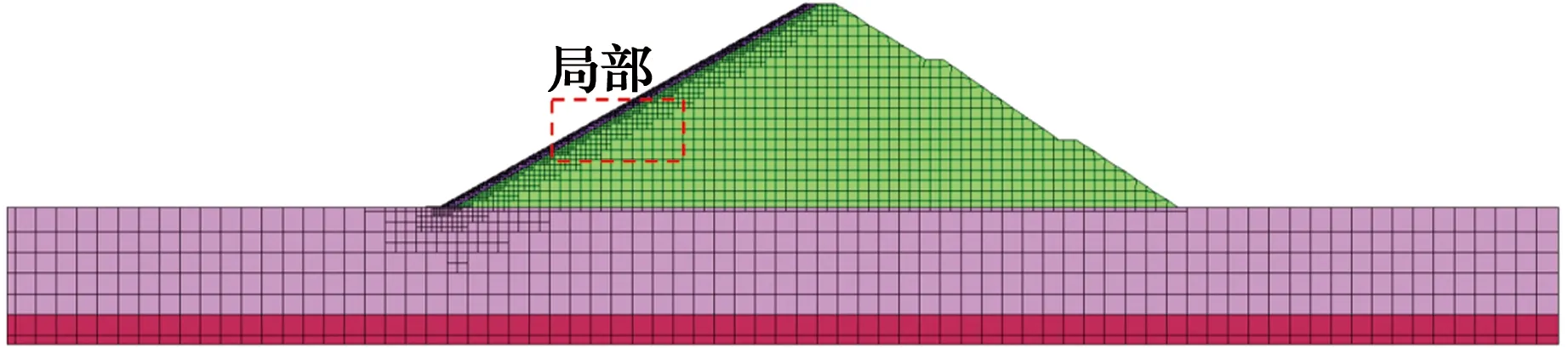
图10 面板坝四分树网格Fig.10 Quadtree mesh of concrete face

图11 面板坝四分树网格局部Fig.11 Partial quadtree mesh of concrete face

静力计算分25个荷载步模拟实际施工过程，分30步缓慢蓄水至152 m高程，静力计算所得的应力变形作为初始应力输入，进行动力时程分析，相应的计算参数列于表2～表4。地震动激励输入如图5所示。

2.2 计算结果分析

图12 满蓄期面板应力变形Fig.12 Deflection and stress along slope direction of

地震动作用下，面板动应力分布情况绘制于图13。从图13可看出：面板应力有少量差别，其中，SBPFEM计算的最大顺坡向应力最大值为13.2 MPa，FEM计算的最大值则为12.2 MPa。最小顺坡向应力计算中，SBPFEM最大压应力为6.91 MPa，最大拉应力为2.21 MPa；FEM计算的最大压应力为5.92 MPa，最大拉应力为2.96 MPa，详细结果列于表7。两种方法计算所得规律基本一致，仅数值有少量差别。

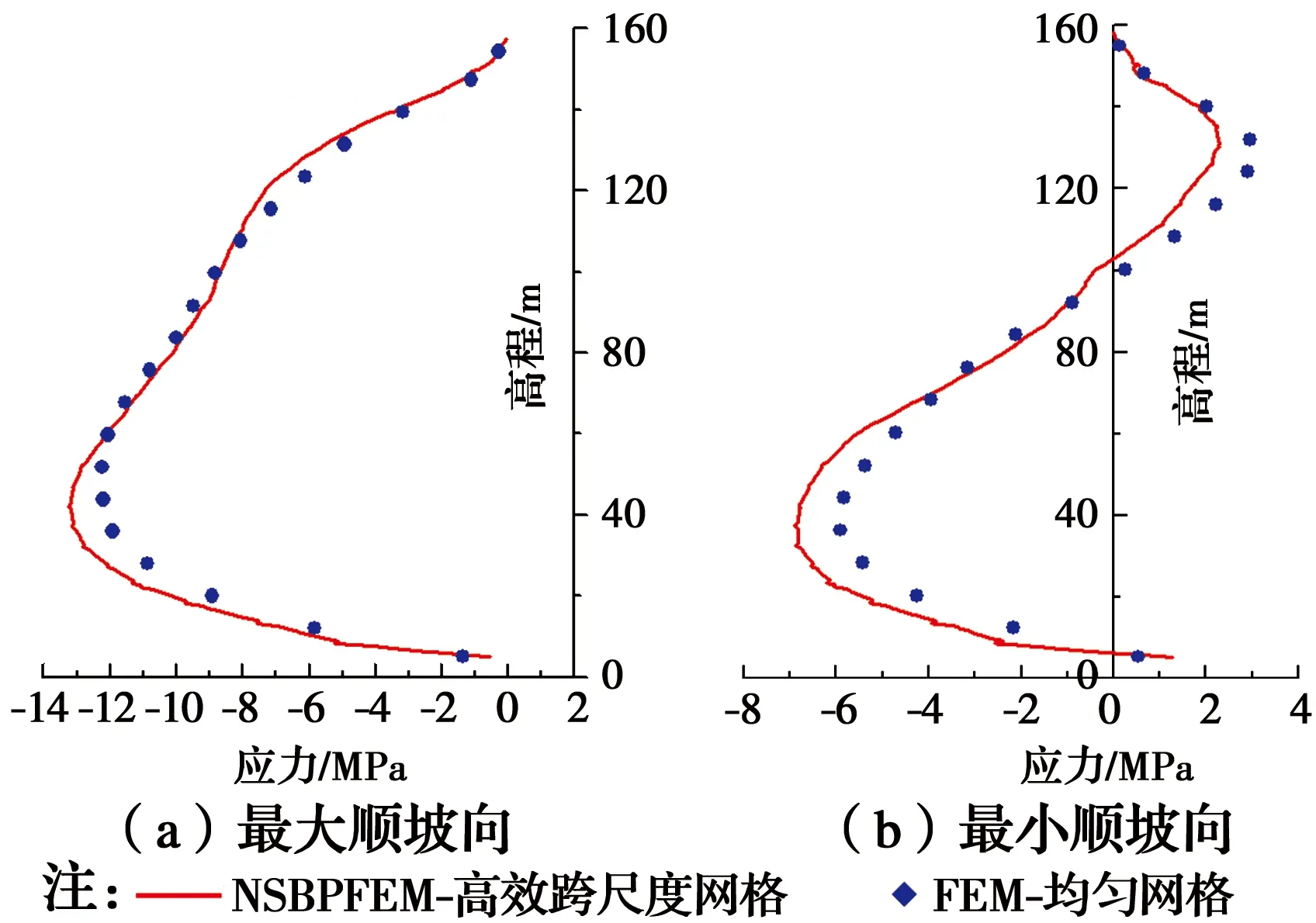
图13 地震作用下面板应力(压为负)Fig.13 Stress along slope direction of concrete face

方法最大顺坡向最大压应力/MPa最小顺坡向最大压应力/MPa最大拉应力/MPaFEM12.25.922.96NSBPEM13.26.912.21

联合NSBPFE和四分树网格技术，对面板坝进行跨尺度精细化静动力数值分析，计算结果符合堆石坝正常变形的基本规律，且FEM计算结果与NSBPFE结果很接近，采用跨尺度方案后，对满蓄期坝体位移及面板应力变形影响不大，但对地震作用下面板应力影响较为明显，最大应力差别约1.0 MPa。

总体来看，可以认为NSBPFEM用于跨尺度精细化分析是合理和可行的，可为下一步研究损伤演化和局部破坏提供了技术支撑。

3 结论

采用自主开发的非线性比例边界多边形单元(NSBPFE)对典型面板堆石坝系统地进行了静力、动力计算分析，结果表明：

1)NSBPFE可简单、便捷地处理三角形、四边形以及传统有限元不能直接处理的五边形、六边形等多边形单元，对堆石坝结构进行系统的静力、动力和永久变形分析，表明该方法结果合理，精度较高，可用于面板坝数值分析。

2)NSBPFE具有更强的灵活性、高效性和通用性优势，主要体现为该方法可与四分树网格技术(多节点单元)自动地无缝结合，以进行面板坝高效的跨尺度精细化分析。

3)研究工作为进一步分析面板坝防渗面板结构局部损伤演化和渐进破坏提供了有力的技术支撑，且具有较强的通用性，可以拓展到其他土木和水利工程的安全评价。