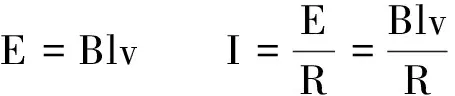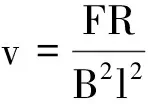动量定理和微元法的妙用

彭爱国

(武汉市第三中学 湖北 武汉 430050)

在磁场中做切割磁感线运动的导体，受安培力作用做变加速运动时，它的速度、位移和运动时间，在中学阶段，用牛顿第二定律和运动学公式无法直接求解，但运用动量定理和微元法的思想则可定量求解前者无法解决的问题.

1 用动量定理和微元法求变加速运动的速度

【例1】如图1所示，一边长为L、电阻为R的正方形导线框以速度v0进入磁感应强度为B的匀强有界磁场，有界磁场的宽度大于L，已知穿过有界磁场后的速度为v′，求线框全部进入磁场时线框的速度大小.

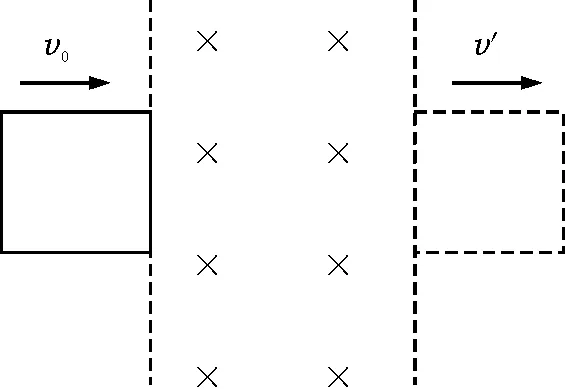
图1 例1题图

分析与解：设线框质量为m，全部进入磁场时的速度为v，线框进入磁场的过程，由动量定理有

(1)

(2)

由式(1)和(2)可得

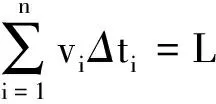
即

(3)

线框出磁场的过程，同理有

即

(4)

由式(3)和(4)可得

【例2】如图2所示，水平导轨abcd与efgh在e和h处相连接，并与光滑的弧形导轨在水平位置相切.匀强磁场竖直向上穿过水平导轨区域，已知导轨abcd的宽度是efgh宽度的2倍，金属棒P和Q的质量分别为m和2m，其中Q棒静止放在efgh轨道上.各轨道都足够长，不计一切摩擦和轨道的电阻，现将P棒从距水平轨道高为H处由静止释放，求棒P和Q的最终速度分别是多少？

分析与解：设P棒进入磁场时的速度为v0，由动能定理

得

(1)

当两个金属棒的速度稳定时，回路中的感应电流为零，设金属棒P的速度减小到v1，金属棒Q的速度增大到v2，则有

2BLv1-BLv2=0

即

v2=2v1

(2)

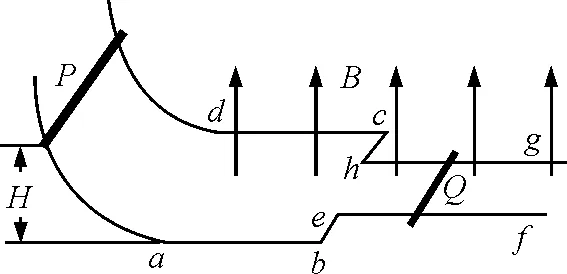
图2 例2题图

对金属棒P，由动量定理有

(3)

对金属棒Q，由动量定理有

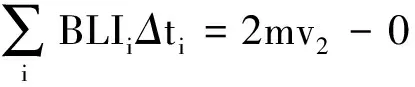
(4)

由式(1)～(4)解得

(5)

2 用动量定理和微元法求变加速运动的位移

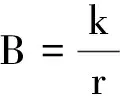
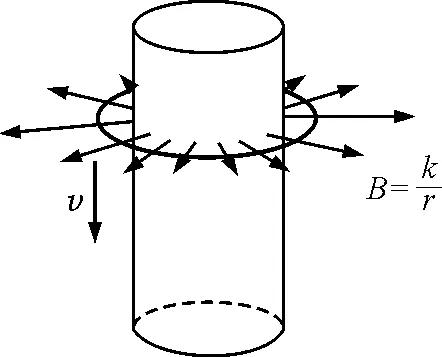
图3 例3题图

分析与解：当圆环加速度a=0时，速度达到最终速度vm，此时有

F安=mg

(1)

E=B×2πRvm

(2)

(3)

F安=BI×2πR

(4)

(5)

由式(1)～(5)解得

由动量定理有

(6)

(7)

由式(5)～(7)解得

3 用动量定理和微元法求变加速运动的时间

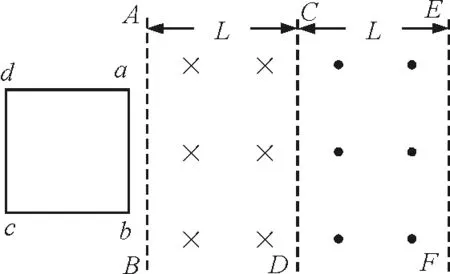
【例4】如图4所示，在光滑的水平面上，有两宽度均为L的有界匀强磁场，3条平行直线AB,CD,EF为磁场的边界，两磁场的方向相反，且垂直桌面，磁场的磁感强度均为B，一边长为l(l

图4 例4题图

线框匀速运动时有

BIl=F

得

线框通过CD分界线的过程，安培力的冲量

同理可得线框出磁场的过程，安培力的冲量

全过程，由动量定理有

Ft+I1+I2+I3=mv

联立上式解得

利用动量定理和微元求和的思想可巧妙求解电磁感应中做变加速运动的导棒的速度、位移和时间,此方法也可推广到一般：当物体受一与其速度大小成正比的力(如阻力f=kv等)和其他恒力共同作用下做变加速直线运动时，对任一过程，只要已知该过程的初速v1、末速v2、位移x、时间t中任意3个，便可用动量定理和微元法求解第4个物理量.