物理核心素养之模型建构测试水平分析2018年高考理综全国Ⅱ卷部分试题为例——以

陈铭 侯恕

(东北师范大学物理学院 吉林 长春 130000)

进入21世纪，随着获取知识渠道的增多，学生获取知识碎片化、浅表化现象日益严重.在这样的背景下，教师需要引导学生进行深度学习.深度学习指学习者在学习过程中深度加工知识信息、深度理解复杂概念、深度掌握内在含义、主动建构个人知识体系并有效迁移应用到真实情境中解决复杂问题[1].学生需要对学习的知识进行分析，探索物理本质.对信息进行加工的结果往往是能够代表物理本质的物理模型，因此，培养学生“模型建构”能力是学生进行深度学习的需要，同时“模型建构”的能力及建构的模型也是深度学习的结果之一.

同时，《普通高中物理课程标准(2017年版)》将“机械运动与物理模型”列为必修一模块的第一主题.物理学科核心素养中的“科学思维”主要包括模型建构、科学推理、科学论证、质疑创新等要素[2]，“模型建构”作为4要素之首，是基于经验事实建构物理模型的抽象概括过程.当前学生解决问题存在的困难之一是情境较复杂，无法准确提取有效信息，建构物理模型.然而,只有将真实的情境转化为物理模型，才能进一步进行科学推理、科学论证等.因此，培养学生“模型建构”能力是培养学生“科学思维”的需要，是进行科学推理、科学论证、质疑创新的基础.

由此，教师需要了解物理模型建构的相关知识、新课标对模型建构的要求及高考如何对学生模型建构能力进行考察.

1 物理模型的内涵及分类

物理模型是对研究对象进行抽象概括而形成的物理表达.研究对象可以是某一物体、过程、系统或问题情境，进行抽象概括的目的是将复杂问题简单化、清晰化，为解决问题做准备.同时，建构物理模型，可以发现问题的本质，将多个问题转化为同一问题，并找到解决这一问题的范式.因此，物理模型不只包含对某一物体、过程、系统的抽象，还包含对问题情境的抽象.

按照抽象概括的对象，笔者将物理模型分为理想物体模型、理想过程模型、状态模型、条件模型和问题模型.其中理想物体模型、理想过程模型、理想状态模型与条件模型将应用于问题模型中.理想物体模型指研究某一物体某一性质时，为研究问题而构建的理想模型.例如,质点、点电荷、轻绳、轻杆、单摆、轻质弹簧、电场线、磁感线等；理想过程模型指将某一过程理想化、简单化并突出这一过程的特征，进而探索针对这一过程的解决办法.例如,匀速直线运动、匀变速直线运动、平抛运动、类平抛运动、圆周运动、碰撞等.理想状态模型指对研究对象某一时刻的状态进行抽象概括.例如,平衡状态、静止状态、理想气体状态等.条件模型指把实际情境中的条件理想化而出现的模型.例如,光滑轨道模型、水平地面模型、匀强电场模型、不计空气阻力等.而问题模型是在教学过程中对一种典型问题的抽象，找到一类问题的共同特征，并将其概括为一种解决问题的范式，问题模型可能包含理想物体模型、状态模型、理想过程模型和条件模型.例如，环绕天体模型、小船渡河模型、板块模型、传送带模型等.问题模型的识别与建构是学生能否将情境转化为物理模型的关键.

2 物理模型建构水平分析

《普通高中物理课程标准(2017年版)》将物理模型分为5个水平[3]，如表1所示.

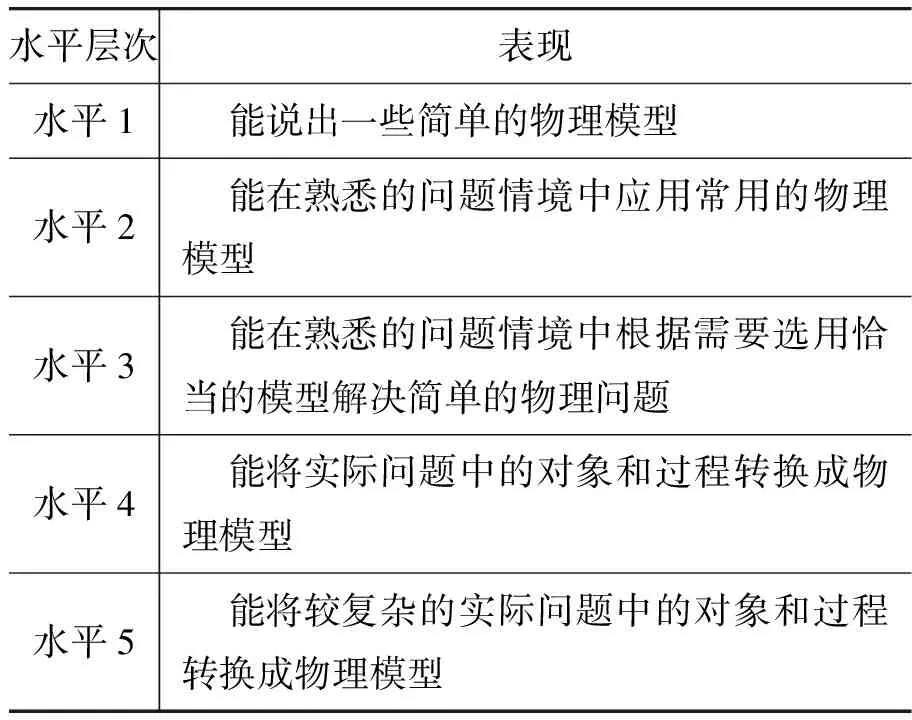
表1 物理模型水平划分

由表1可知：水平1与水平2的差异在于是否能应用常见的模型；水平2与水平3的差异在于是否能选用恰当的模型，并解决简单的问题；水平3与水平4的差异在于是否能够将实际问题转化为物理模型；水平4与水平5的差异在于问题的复杂程度.其中水平1，2，3仅涉及模型的识别与选用，未涉及建构模型；水平4，5涉及建构模型.依据《普通高中物理课程标准(2017年版)》，水平2是高中毕业生应达到的合格要求，是学业水平合格性考试的命题依据；水平4是用于高等院校招生录取的学业水平等级性考试的命题依据[4].由此可知，高中阶段的学习不要求学生达到水平5.能够将生活中遇到的一般问题转换成物理模型并解决问题即可.将实际问题转换为模型是问题解决的基础.

3 提升学生模型建构能力的实践探索

基于以上分析，教学中，应如何培养学生的模型建构能力呢，结合学生实际，对培养高一学生模型建构能力做了实践探索，并提出以下3条教学策略.

3.1 创设情境 引导学生以情境为起点分析问题

新课教学时，教师应铺设情境，该情境可以来自生产生活、科技前沿、工程制造、物理学史等领域，引导学生从情境中发现并建构物理模型，将情境抽象为物理问题，培养学生从情境中提取信息，建构物理模型的能力.例如,“平抛运动”一节，对平抛运动进行处理时，给出情境：1945年3月10日，第二次世界大战期间，美国陆军航空队对日本东京进行了大规模的战略轰炸，匀速飞行的飞机在10 000米的高空投弹，为什么航空员在飞机上看炸弹竖直下落而地面上的人看炸弹不是竖直下落？学生需要将炸弹丢出后的运动转化为平抛运动模型，识别飞机运动为匀速直线运动，对比得出平抛运动水平方向为匀速直线运动.再如，进行牛顿第三定律教学时，给出情境：小明猛然蹲下和跳起的过程，试分析这个过程中，小明对地面的压力、地面对小明的支持力及小明的重力之间的关系.学生需要将小明看做质点，分析小明蹲下及跳起过程中的运动情况，进而确定小明所受重力与地面对小明支持力之间的关系.识别出小明对地面的压力和地面对小明的支持力是一对相互作用力，无论何种运动状态，两力大小均相等.引导学生以情境为起点分析问题，识别情境中的模型，选用恰当的模型解决情境中的问题.

3.2 概括问题模型 寻找不同情境的本质

教学中，我们常遇到一类问题，对于这类问题有同一个解决范式，俗语称其为“换汤不换药”.然而，学生在学习中，却很难识别出这些问题属同一类问题，如果学生能够找到这类问题的本质，将同类问题看做一个问题，那么学习物理的难度将大大降低.教学中，教师也常说“木板-滑块模型”“传送带模型”“小船渡河模型”“拉船靠岸模型”“双星模型”等，这里所说的“模型”，是对一类问题的概括.以“拉船靠岸模型”为例，它不仅指“拉船靠岸”这一情境，而指与“拉船靠岸”问题本质相同的一类问题.“拉船靠岸”的本质是绳上任一点速度大小相同，如图1所示.岸上人拉绳，由于绳不伸长，绳上A点沿绳速度大小与B点沿绳速度大小相等，即v1=v0，而B点实际速度是v船，所以需将其分解，找到沿绳方向的速度，为找到沿绳方向的全部速度，故需将v船按照沿绳和垂直于绳的方向进行分解，由v1=v0即可解决此类问题.

图1 拉船靠岸

“拉船靠岸模型”的本质是绳上各点沿绳速度相等，找到沿绳方向的所有速度.概括该问题模型后，给出另一情境：如图2所示，木杆靠着墙面下滑，已知A点的速度为vA，求B点的速度vB.对本题进行分析，发现求解的关键在于杆上各点沿杆速度大小相等，该问题可用“拉船靠岸模型”的解答范式进行求解.因此，教学过程中，要概括问题模型，找到此类问题的本质，引导学生将多个情境转化为一个问题，提升模型建构能力.

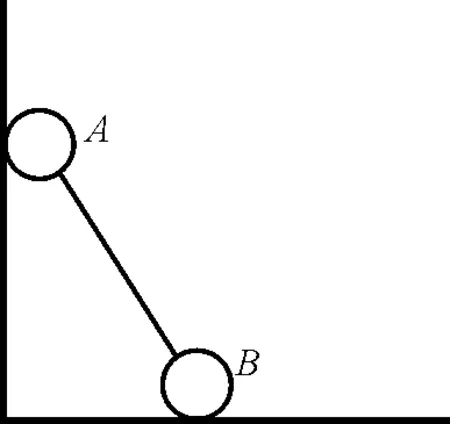
图2 杆沿墙下滑

3.3 引导学生自主建构学科知识体系

物理学科的知识严谨且框架清晰，引导学生及时自主建构知识体系，不仅对知识的理解有帮助，对学生的建构能力也有所帮助.教师要在这一过程中做好引导，强调积累，关注学生将零散的知识结成知识网的过程.解决实际问题时，能够尽快选择或建构恰当的模型，对问题进行求解.

4 物理高考题中模型建构测试水平分析

基于新课标对物理模型的水平划分及课堂教学对学生模型建构能力的培养，对2018年高考理综全国Ⅱ卷部分试题就“模型建构”方面进行分析.

【例1】(2018年高考理综全国Ⅱ卷第15题)高空坠物极易对行人造成伤害.若一个50 g的鸡蛋从一居民楼的25层坠下，与地面的撞击时间约为2 ms，则该鸡蛋对地面产生的冲击力约为( )

A. 10 N B. 102N

C. 103N D. 104N

分析：本题选取了生活场景作为问题情境.需要学生识别鸡蛋下落可近似看做自由落体运动，选用自由落体模型估算鸡蛋接触地面时的速度，然后运用碰撞模型估算冲击力的大小.即根据生活情境，选用自由落体模型和碰撞模型两个过程模型，并解决问题.对照表1，“鸡蛋落地”属于生活中常见的生活情境，学生要从知识库中选择恰当的模型解决问题，因此，本题对“模型建构”的考察符合水平3.

解答：鸡蛋下落近似看做自由落体运动，则接触地面时的速度

撞击地面为碰撞模型，由动量定理得

(N-mg)t=0-(-mv)

代入数据，解得

N≈103N

选择C.

【例2】(2018年高考理综全国Ⅱ卷第16题)2018年2月，我国500 m口径射电望远镜(天眼)发现毫秒脉冲星“J0318+0253”，其自转周期T=5.19 ms，假设星体为质量均匀分布的球体，已知万有引力常量为6.67×1011N·m2/kg2.以周期T稳定自转的星体的密度最小值约为( )

A.5×109kg/m3B. 5×1012kg/m3

C.5×1015kg/m3D. 5×1018kg/m3

分析：本题选取了科技前沿为问题情境.需要学生识别“星体稳定自转”指星体任意部分能够做半径一定的匀速圆周运动，将研究对象确定为星体表面的某一质点，将研究过程看做匀速圆周运动，将这一问题转化为“表面环绕”问题模型，即可解决问题.对照表1，要将星体转动这一过程转化为匀速圆周运动过程模型，本题对“模型建构”的考察符合水平4.

解答：构建“表面环绕”问题模型，万有引力提供星体表面质点做匀速圆周运动所需的向心力，即

且

代入数据得

ρ≈5×1015kg/m3

选择C.

【例3】(2018年高考理综全国Ⅱ卷第24题)汽车A在水平冰雪路面上行驶，驾驶员发现其正前方停有汽车B，立即采取制动措施，但仍然撞上了汽车B.两车碰撞时和两车都完全停止后的位置如图3所示，碰撞后B车向前滑动了4.5 m，A车向前滑动了2.0 m，已知A和B的质量分别为2×103kg和1.5×103kg，两车与该冰雪路面间的动摩擦因数均为0.10，两车碰撞时间极短，在碰撞后车轮均没有滚动，重力加速度大小g=10 m/s2.求：

(1)碰撞后的瞬间B车速度的大小；

(2)碰撞前的瞬间A车速度的大小.

图3 A车与B车碰撞前后的位置

分析：本题选取了生活场景作为问题情境.需要学生将两车看做质点，分析两车的运动情况，将此情境转化为匀变速直线运动模型和碰撞模型，再进行科学推理，从而求解.对照表1，本题要把两车的实际运动转化为匀变速直线运动模型求解，并识别出碰撞模型，因此，本题对“模型建构”的考察水平符合水平4.

解答：(1)B车碰撞后做匀减速直线运动.

由牛顿第二定律得，B车碰撞后加速度大小

由匀变速直线运动规律

得

(2)A车碰撞后做匀减速直线运动，同(1)可得,A车碰撞后的速度为

vA=2 m/s

A车与B车碰撞，动量守恒.可得

代入数据得,碰撞前

有部分同学在第二问解答中出现问题，列了机械能守恒方程，究其原因，实则是选择的模型不对，本题为一般碰撞模型，而非弹性碰撞模型.

【例4】(2018年高考理综全国Ⅱ卷第34题)声波在空气中的传播速度为340 m/s，在钢铁中的传播速度为4 900 m/s.一平直桥由钢铁制成，某同学用锤子敲击一铁桥的一端而发出声音，分别经空气和桥传到另一端的时间之差为1.00 s.桥的长度为______m，若该波在空气中的波长为λ，则它在钢铁中的波长为λ的______倍.

分析：本题选取了工程问题为问题情境.需要学生从问题情境中识别并选用机械波模型，机械波在均匀介质中匀速传播，再运用机械波波长与波速的关系解决问题.对照表1，本题是学生熟悉的声音传播的情境，需要学生选用机械波波长与波速关系这一数学模型解决问题，因此，本题对“模型建构”的考察水平符合水平3.

解答：声波传播符合机械波传播规律.在空气中传播所需的时间

在钢铁中传播所需的时间

由题知

t2-t1=1 s

解得

l=365 m

对2018年高考理综全国Ⅱ卷的4个典型例题的分析可知：高考题对“模型建构”的考察，通常会设置问题情境，这一情境来自生产生活、科技前沿及工程制造，学生需要从问题情境中抓住问题本质，识别、提取、建构物理模型，并链接模型相关的知识，进行科学推理，解决问题；高考题中对“模型建构”的考察水平集中在水平3和水平4.

教学中常有人说“学生基础知识还不错，就是不会用”.这里的“用”常常指将具体情境抽象为物理模型这一过程，抽象为物理模型后，链接模型对应的知识，知识便“用”上了.也有人说“学生公式记住了，但在具体问题中，无法把公式中的各个物理量具体化”，这也是“模型建构”出问题的一个表现.这里的“具体化”指学生从问题情境中识别并提取物理模型，能够识别、提取出物理模型，便能将问题情境中的物理量与具体的物理概念、规律相对应.因此，提升学生的“模型建构”能力是解决知识不会“用”以及无法将知识“具体化”的出路.

综上，“模型建构”是“科学思维”中关键要素之一，对2018年高考理综全国Ⅱ卷分析可知，学生要从情境中识别、提取、建构物理模型，模型建构能力应达到水平4.在教学中教师要有培养学生模型建构能力的意识，引导学生以情境为起点分析问题，并概括问题模型，引导学生在生产生活、科技前沿、工程制造等情境中，将物理知识“用”起来.