一种提升空调换热的室外机分布式流路模型开发

张浩，何哲旺，武滔,2，吴国明，任滔，丁国良*

（1-广东美的制冷设备有限公司，广东佛山 528311；2-重庆大学城市建议与环境工程学院，重庆 400044；3-上海交通大学制冷与低温工程研究所，上海 200240）

0 引言

由于高效紧凑化空调器的发展趋势，空调的室外换热器通常采用更小管径的铜管来提升空调器的换热性能[1-2]。空调室外换热器的管径减小会导致管内压降增加[3-4]，不利于换热器的性能进一步提升。目前的空调器通常采用多流路室外换热器来降低管内压降并提升空调器的性能[5]。

多流路室外换热器最常见的问题是常规的流路设计无法保证空调器在不同的冷媒流动特性下始终处于最佳的换热状态[6-7]。制冷剂的物性，比如流速、温度、压力等等，在换热器的进口阶段和出口阶段相差很大[8-9]。不同的制冷剂物性具有不同的压降特性，从而需要不同的分流方案才能达到最佳的换热。目前室外换热器通常采用均一分流数目的流路[10-12]，无法保证换热器内所有的制冷剂均具有最佳的分流特性和换热特性。

解决换热器内冷媒物性不同导致的分流问题的方法是在换热器的不同位置处采用不同的分流方案[13-14]。当制冷剂的干度很大时，制冷剂的流速较大[15-16]，导致压降很大；此时制冷剂需要较大的分流数目来减少压降，以便达到更好的换热。当制冷剂的干度很小时，制冷剂的流速很小，导致制冷剂的换热系数很小；此时制冷剂需要更少的分流数目来增大换热系数。

根据冷媒物性的变化设计新型流路的难点在于制冷剂物性和对应的分流特性之间的理论关系未知。新型流路需要根据制冷剂的物性精确计算对应的分流特性[17-18]。但是目前还没有关于制冷剂物性和分流特性的相关理论研究。因此有必要开展制冷剂流动特性和分流特性的理论研究。

本文的目的是提出一种能够提升空调换热的室外机分布式流路。

1 分布式流路模型开发原理

室外换热器分布式流路模型开发思路是：针对换热微元建立分流模型，求解使得微元换热量最大的临界质流密度；并通过换热器分流模型求解分布式流路，使得每个换热微元的制冷剂质流密度尽可能地接近极限质流密度。

临界质流密度Gcri是使得换热微元换热量最大的质流密度，由管内制冷剂干度和制冷剂流量决定。不同换热器位置处的制冷剂具有不同的干度和流量，如图1(a)所示。在流路的入口阶段，制冷剂干度小，液相制冷剂体积远大于气相制冷剂体积，使得管内制冷剂流速很小。此时管内具有很小的压降和很小的换热系数，如图1(b)所示。这说明换热器需要通过减小分流数目，来提高质流密度G和换热系数。当制冷剂流到室外机管程的中部时，气相制冷剂逐渐增多，导致制冷剂流速增大，使得管内制冷剂的压降和换热系数同时升高，并达到一个最佳的匹配，如图1(c)所示。当制冷剂处于室外机管程的出口阶段，制冷剂的干度很大，气相制冷剂体积远大于液相制冷剂体积，使得管内制冷剂流速非常大，如图1(d)。此时制冷剂的压降非常大，严重影响了管内换热的换热温差。

整个换热器的分布式流路通过求解换热器分流模型得到。换热器分流模型以一根U管为最小换热单元，分别求解每一根U管的最佳分流方案，最终得到整个换热器的分布式流路。

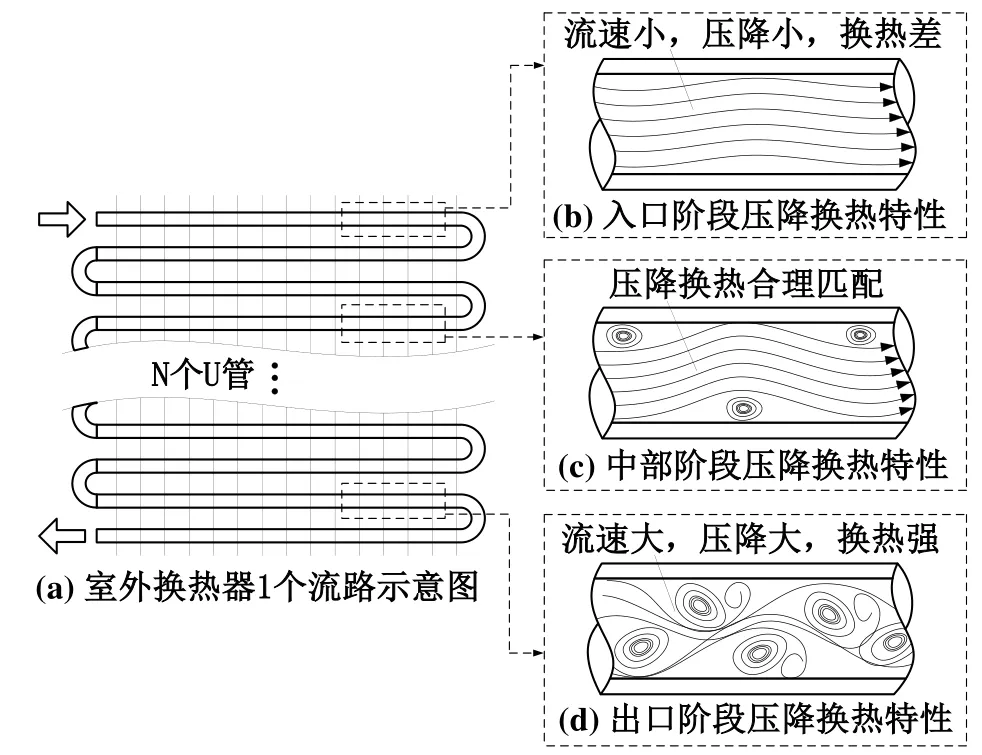
图1 室外换热器制热工况下不同管程的换热压降特性

2 换热微元分流模型

首先建立换热微元换热的控制方程，确定换热微元的边界条件和补充方程，然后求解换热微元分流模型得到使换热微元换热量最大的临界质流密度Gcri和对应的最佳分流数Nopt。

2.1 换热微元分流模型控制方程

换热微元分流的控制方程包括 1个换热量方程和3个能量平衡方程。换热量方程计算换热微元内的空气与制冷剂之间的换热量，用于评价室外换热器的换热性能。能量平衡方程是分别基于空气侧热平衡、制冷剂侧热平衡以及空气-制冷剂之间热平衡获得。

换热量方程是通过换热微元内的制冷剂焓差变化得到。换热微元是沿换热器管程方向上选取的一个ds长度的微小换热段，如图2(a)所示。换热微元的换热量由制冷剂的进出口焓差和制冷剂质量流量计算得到，如公式1和图2(b)所示。

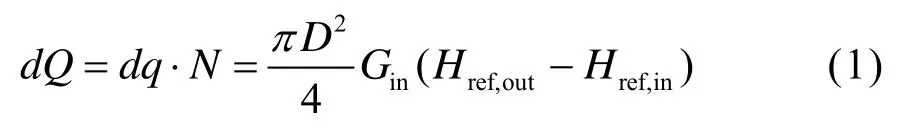
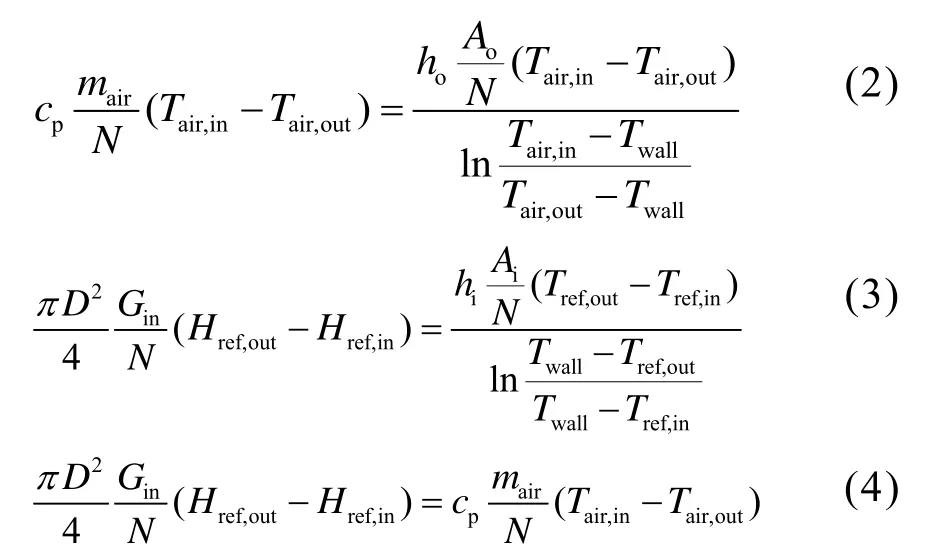
能量平衡方程是在换热微元被分成N个流路后针对每个流路微元建立的，如图3所示。换热微元被分成N个流路后，每个流路微元的长度为ds/N，管内面积为Ai/N，管外面积为Ao/N，进口制冷剂质流密度为Gin/N，进口空气流量为mair/N。空气侧温度变化导致的能量变化是由空气与铜管外壁面换热导致的，如公式2所示；制冷剂侧焓差的变化是由制冷剂与铜管内壁面换热导致的，如公式3所示；在微元换热稳定后，空气侧的能量变化等于制冷剂侧的能量变化，如公式4所示。换热微元的4个控制方程中含有 7个未知参数，即 Twall、Tref,out、Tair,out、dQ、N、hi、Href,out。因此需要添加补充方程，才能求解换热微元的控制方程组。

式中：

D——管径，m；

ds——管程，m；

Ao——管外换热面积，m2；

Ai——管内换热面积，m2；

Tair,in——空气进风温度，K；

mair——空气流量，kg/s；

ho——空气侧换热系数，kJ/(kg⋅K)；

Tair,out——出风温度，K；

G——冷媒质流密度，kg/(m2⋅s)；

x——干度，无量纲；

p——压力，Pa；

T——温度，K；

hi——管内换热系数，W/(m2⋅K)。

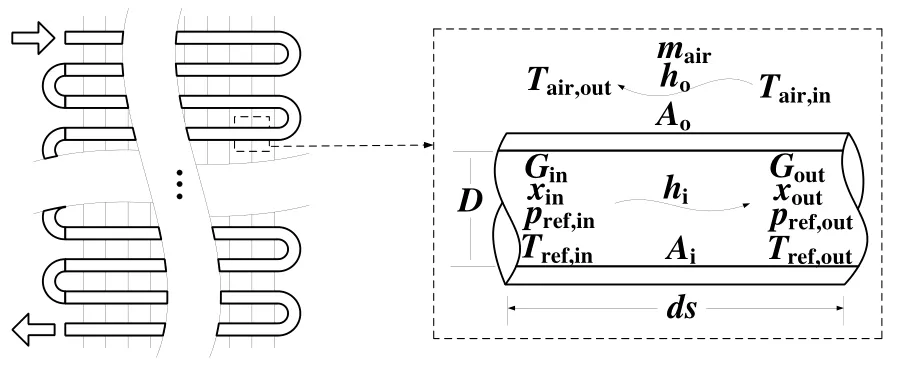
图2 换热微元内的结构参数和换热参数

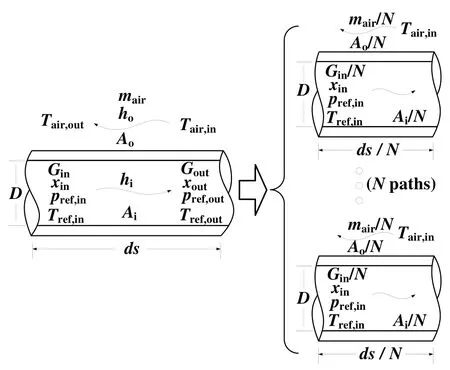
图3 换热微元被分成N个流路后的参数变化

2.2 换热微元分流模型补充方程

补充方程包括管内换热系数 hi计算方程和管内压降Δp计算方程。管内换热系数hi采用GUNGOR的经验公式计算[19]，其平均计算精度经过试验验证为17.6%以内。管内压降采用胡海涛的经验公式计算[20]，其平均计算精度经过试验验证为10.8%以内。

2.3 换热微元分流模型求解结果

4个控制方程和2个补充方程组成的换热微元分流方程组中包括7个未知参数，即Twall、Tref,out、Tair,out、dQ、N、hi、Href,out。换热微元分流方程组存在无数个解，即每一个分流数N均对应一个微元换热量 dQ。在无数个解当中，存在一个分流数 Nopt会产生最大的微元换热量 dQmax。此时微元内的质流密度即为临界质流密度。

临界质流密度Gcri的求解方法是：

1）首先假设一个分流数N值，带入 Δp补充方程，求解得制冷剂出口压力 pref,out和制冷剂出口温度Tref,out；

2）再将分流数N和制冷剂出口温度Tref,out带入控制方程和 hi补充方程，求解空气出风温度Tair,out，制冷剂出口焓Hout和微元总换热量dQ；

3）循环计算，直到总换热量 dQ 达到最大，并输出临界质流密度Gcri和最佳分流数Nopt，如图4所示。

临界质流密度Gcri的求解结果如图5所示。临界质流密度Gcri随着冷媒干度增大而减小，表明换热微元的最佳分流数目随着制冷剂的干度增大而增大。

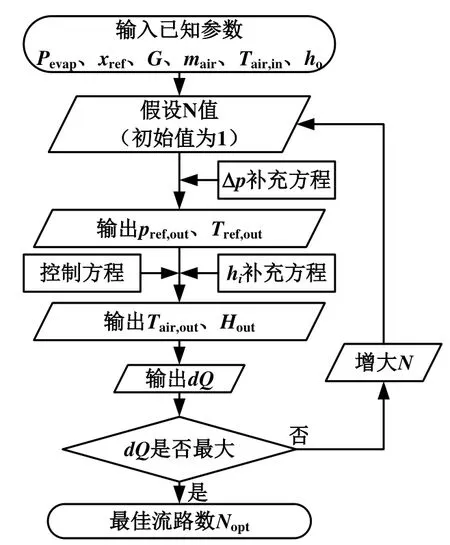
图4 换热微元最佳分流求解思路

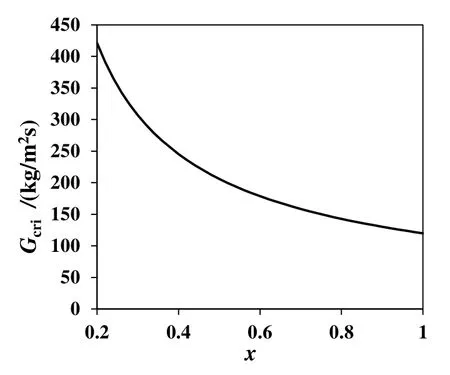
图5 换热微元临界质流密度求解结果

3 换热器分流模型

室外换热器分布式流路通过求解换热器分流模型得到。换热器分流模型是以单位U管长度的换热量为目标函数，求解使得单位U管长度换热量最大的分流方案，如公式5所示。

式中：

Q——换热量，W；

ds——计算单元的长度，m；

Ni——第i轮的分流数目；

L——U管长度，m。

分布式分流模型进行若干轮分流计算，并且每一轮各个分流支路的制冷剂均流过1个U管后进入汇总管等待下一轮的分流计算，如图6(a)所示。在每一轮分流之前，分布式流路模型均进行一次最佳分流数的求解，使得室外换热器的任何一个U管内的制冷剂质流密度尽可能地接近临界质流密度Gcri，如图6(b)所示。

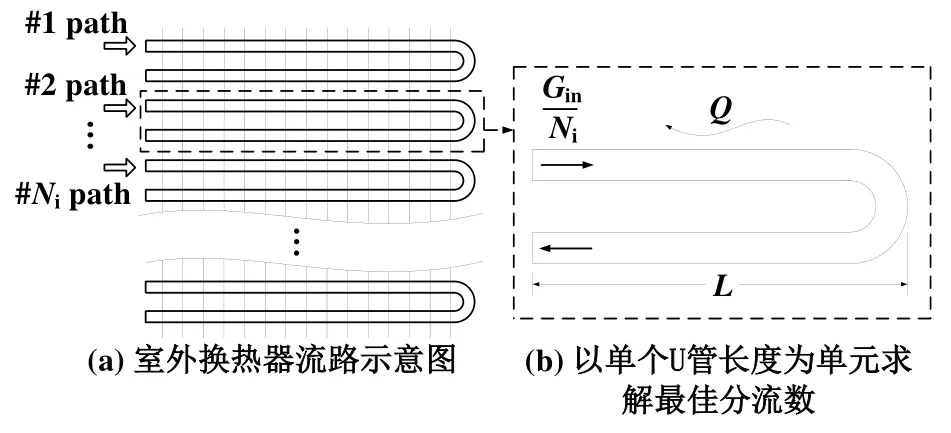
图6 室外换热器分布式流路设计方法

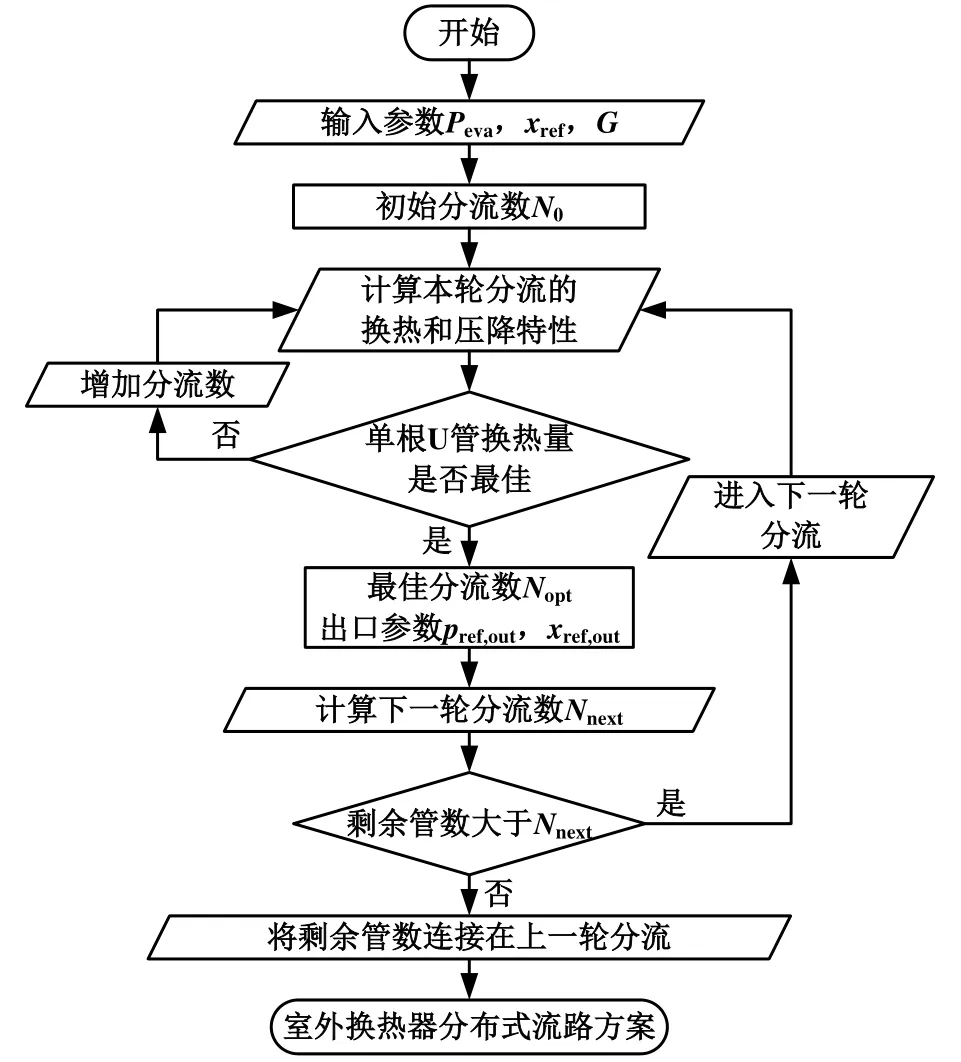
图7 室外换热器分布式流路求解思路

换热器分流模型的求解，如图7所示，主要包括以下5个步骤：

1）分流前，进行最佳分流数目求解，获得使单位U管长度的换热量最大的分流数目，即最佳分流数目Ni；

2）求解最佳分流数目Ni后，制冷剂按照最佳分流数目分别流入Ni个U管；

3）在流过1个U管长度后，所有制冷剂进入汇聚管等待下一次的分流；

4）计算下一次分流的最佳分流数目Ni+1，如果剩余U管数目大于Ni+1，则进入下一次分流；

5）重复步骤1）至4），直到剩余U管数目不足，即剩余U管数目小于下一次分流数目Ni+1，则将剩余的U管连接到上一次分流中，室外换热器分布式流路设计结束。

4 案例分析

为了更清楚地展示室外换热器分布式流路的设计方法，本文提供一个案例的设计过程。

步骤1：输入室外换热器结构参数和运行参数，如表1所示。计算管内面积Ai，管外面积Ao，管外换热系数ho，制冷剂进口压力prefer,in，制冷剂进口干度xin，制冷剂进口焓Hin，制冷剂质流密度Gin。

步骤2：根据制冷剂进口参数求解第1轮分流的最佳分流数目 N1。计算结果表明最佳分流数目N1为2。故第1轮分流方案是：制冷剂分成两个流路，分别流进1个U管，最后进入汇聚管。

步骤3：计算第1轮分流出口制冷剂状态参数，并根据制冷剂状态参数计算第2轮分流的最佳分流数目N2。第2轮分流的最佳分流数目N2为3。故第2轮分流方案是：制冷剂分成3个流路，分别流进1个U管，最后进入汇聚管。

步骤4：计算第2轮分流出口制冷剂状态参数，并根据制冷剂状态参数计算第3轮分流的最佳分流数目N3。第2轮分流的最佳分流数目N3为4。故第3轮分流方案是：制冷剂分成4个流路，分别流进1个U管，最后进入汇聚管。

步骤5：剩余U管数目为零，分布式流路设计结束。室外换热器的最终流路设计方案是2-3-4流路，如图8(a)所示。

为了比较分布式流路和常规流路的换热特性，本文将2-3-4分布式流路的换热量与2种常规流路进行比较。2种常规流路分别是2流路和3流路，分别如图8(b)和8(c)所示。

室外换热器流路与理论最佳流路之间的性能差异可以通过分析制冷剂沿程质流密度与临界质流密度之间的差异来获得。理论上最佳的流路设计应该满足管程任意位置处的质流密度等于临界质流密度Gcri这个条件。但室外换热器的最小流路长度是1个U管，使得实际流路的制冷剂质流密度呈阶梯状，如图9(a)所示。当实际流路的阶梯状的质流密度越接近临界质流密度 Gcri，表明该流路分流越有利于换热。2-3-4流路的质流密度比2流路和3流路更接近临界质流密度Gcri，表明2-3-4流路的性能比2流路和3流路更好。计算结果表明采用2-3-4分布式流路的室外换热器的额定制热量和低温制热量分别比采用流路数目均一的 3流路的高 8.8%和5.6%，如图9(b)所示。

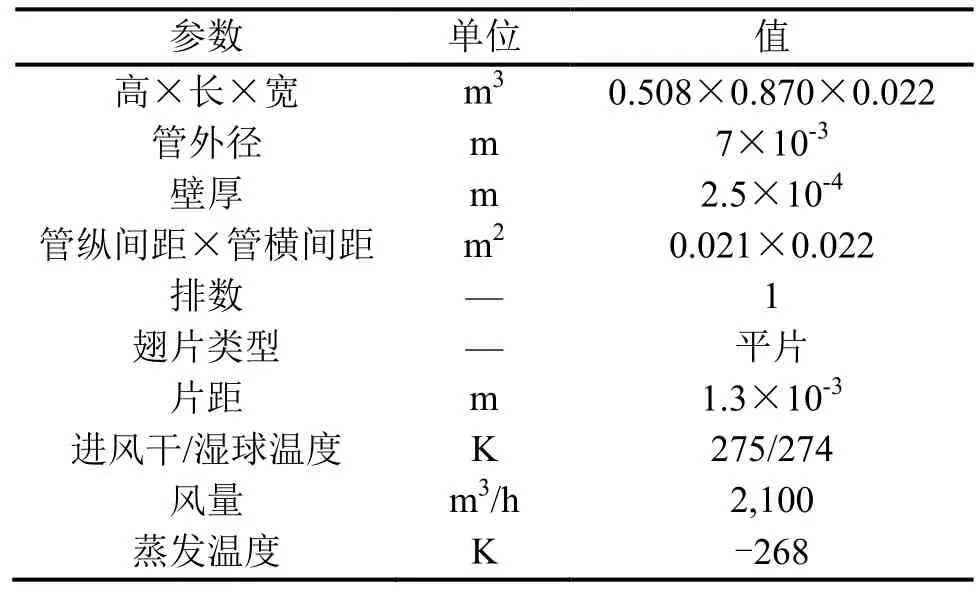
表1 室外换热器输入参数

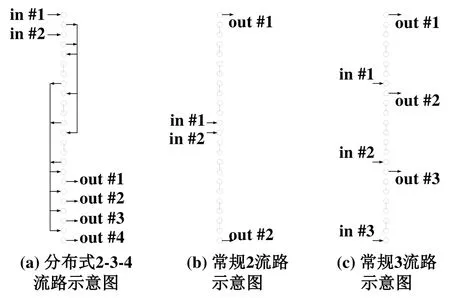
图8 室外换热器流路设计结果

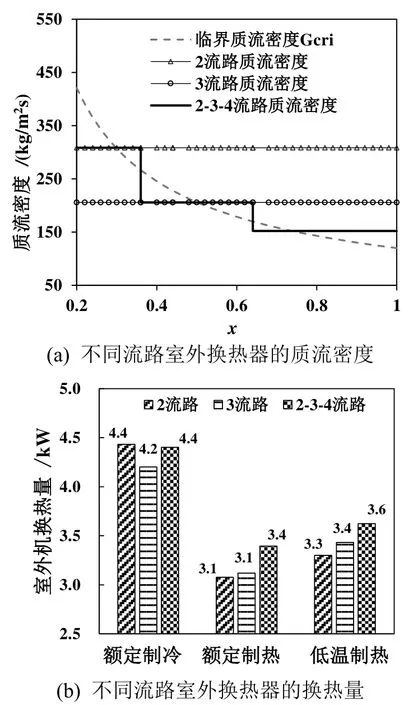
图9 不同流路室外换热器性能分析

5 结论

1）采用分布式流路的室外换热器的额定制热量和低温制热量分别比采用流路数目均一的3流路提高8.8%和5.6%。

2）本文提出的分布式流路设计方法是：针对室外换热器微元建立分流模型，求解使得微元换热量最大的临界质流密度；并通过室外换热器分布式分流模型求解分布式流路，使得室外换热器的制冷剂质流密度尽量接近极限质流密度。

3）临界质流密度可以作为流路设计的评价标准。制冷剂在流路中的沿程质流密度越接近临界质流密度，表明该流路越有利于换热。