航天器热循环试验低温负载工况补偿方法

刘张鹏，王珊珊，张婉雨，吴静怡

（1-上海交通大学机械与动力工程学院制冷与低温工程研究所，上海 200240；2-上海卫星装备研究所，上海 200240）

0 引言

热试验能够检验航天器热设计的正确性，暴露产品的质量缺陷，是最重要的地面环境试验之一。热循环试验在常压环境下进行，传热方式以对流传热为主，相对于热真空试验具有效率高、成本低等优势，近年来在航天器的研制中受到了普遍重视[1]。在低温工况下，热循环试验温度变化范围大，箱体内易产生较大温差，影响试验的可重复性和可靠性，并可能产生局部热应力，对被试航天器造成损伤[2]。因此，针对航天器热循环试验低温工况中温度分布的研究有重要的理论意义与应用价值[3]。

典型的热循环试验箱体一般为规则的矩形截面竖直通道，通过通入高低温气体以达到或维持目标温度[4-5]。低温工况下箱内气体除受入口的惯性力作用外，还在壁面受热浮升力作用，相应的箱内流动为强制对流与自然对流耦合的混合对流[6-7]。JACKSON等[8]的研究表明，管道内混合对流的传热特性主要受Reynolds数、Grashof数以及几何结构等参数影响。YANG等[9]的研究指出，矩形竖直通道内反向浮升力混合对流传热相对于同向浮升力有更好的温度均匀性效果。黄一也等[10]以数值模拟的方法研究了不同运行参数下航天器热循环试验箱内的温度均匀性的变化规律，并设计了控制送风速度和送风温差的温度均匀性优化方法。侯雪川等[11]以理论推导的方法探究了热循环试验中被试产品对温度场分布的影响，发现被试产品相对位置与方向的变化能够引起温度场的复杂改变。

现有的研究多围绕热循环试验空载工况展开，对于负载工况研究较少。本文参考已有研究[12-18]，通过数值模拟方法对航天器热循环试验系统在空载和负载低温工况下的温度场分布进行研究，分析了被试航天器对试验箱内温度场分布的影响，并设计了一种优化试验箱内温度均匀性的补偿方法。

1 模型与方法

已有研究发现，反向浮升力混合对流传热作用下的流场相对于同向浮升力有更好的温度均匀性[6]。据此，本文设计航天器热循环试验系统流程如图 1所示。在低温工况中，系统驱动试验箱内空气进入制冷系统，冷却至目标温度后通入试验箱体。冷气来流在壁面处受到竖直向上的浮升力，因此采取系统气流顺时针流动、箱体内“上进下出”的送风方式，使得浮升力为反向。

本文采用的热循环试验箱及航天器的物理模型如图2(a)所示。箱体为8 m×6 m×7 m的长方体，低温空气经过多孔板整流后以均匀恒定的温度 T∞和速度v∞从顶部或底部进入试验箱，环境温度保持恒温 Tw。航天器模型根据某型号卫星实体结构建立，为壁厚10 mm的密封舱体，材质为铝合金，在负载工况中放置在箱体中央，与底部距离为h=1 m。

为修正负载工况下被试体对流场变温效率和温度场均匀性的负面影响，考虑为试验空间提供垂直于原气体来流的补偿气流。在试验箱体的侧面设置6个补偿气流进风口，每个均为0.5 m×0.5 m的矩形均匀气体来流，距地面h0=4.5 m，同时保持试验空间气体体积流量与原工况相同，称为有补偿的工况，如图2(b)所示。

图1 常压热循环试验系统流程

图2 热循环试验箱及航天器物理模型

本文使用Fluent 6.3进行数值计算，采用RNG k-ε湍流模型及非均匀的结构化网格，并对壁面附近的边界层流动进行标准壁面函数法处理。参考试验系统实际工况条件，设置进风速度为0.01 m/s（体积流量0.64 m3/s）、环境及箱体初始温度为300 K、进风温度为253 K、进气方向为-Y向（上进下出，受反向浮升力）的算例工况1～工况4，如表1所示。

表1 算例计算条件设置

据相关国家标准[19-20]对环境试验温度测量点位置和数量的要求，在试验箱体内设置 14个温度测点，分别位于距地面1 m、3.5 m及6 m的3个平面上，每个平面各有5个温度测点（除距地面3.5 m平面因被试航天器阻隔仅有4个测点)，平面四角的温度测点距宽度方向内壁面为 0.6 m、距长度方向内壁面为 1 m，平面中心的温度测点位于其几何中心位置。此外，为了研究航天器表面附近的温度均匀性，在距航天器表面0.1 m处选取具有代表性的温度测点8个，共计22个测点（如图3所示）。为了定量地描述试验空间内的温度场变化，分别以22个温度测量值的平均值Tavg和标准差σ来表征试验空间温度和温度波动度。

图3 试验箱体温度测点布置

2 结果与讨论

图4给出了4种降温工况下温度分布随时间的变化情况。可以发现，在负载工况下，由于被试体的热容及其对气体来流的阻挡和粘滞作用，试验空间内的降温过程进度明显减缓。有补偿气流的负载工况相对于无补偿负载工况，其降温过程有明显加速，被试体本身的平均温度也更低。

图4 降温过程开始后0～600 s（第1～7行）工况1～4（第1～4列）Z=4截面的温度分布

图5和图6分别给出了4种降温工况下流场平均温度和温度标准差随时间的变化情况。观察图 5可以发现，负载工况的降温效率远落后于空载工况，在降温过程开始600 s后，负载工况的降温幅度仅为空载工况的约 71%。有补偿的负载工况的降温过程相对于无补偿负载工况有明显加速，在降温过程开始 100 s后，其降温幅度为无补偿负载工况的约152%，此时补偿气流一定程度上抵消了被试体对降温进程和温度场均匀性的破坏作用，使得工况 4的曲线一度领先于工况 3的曲线。在降温过程进行约600 s后，由于除被试体外的试验空间降温基本完成，流场内的换热主要发生在冷气流与被试体之间，补偿气流的修正效果减弱，此时有补偿负载工况的降温幅度约为无补偿负载工况的106%。

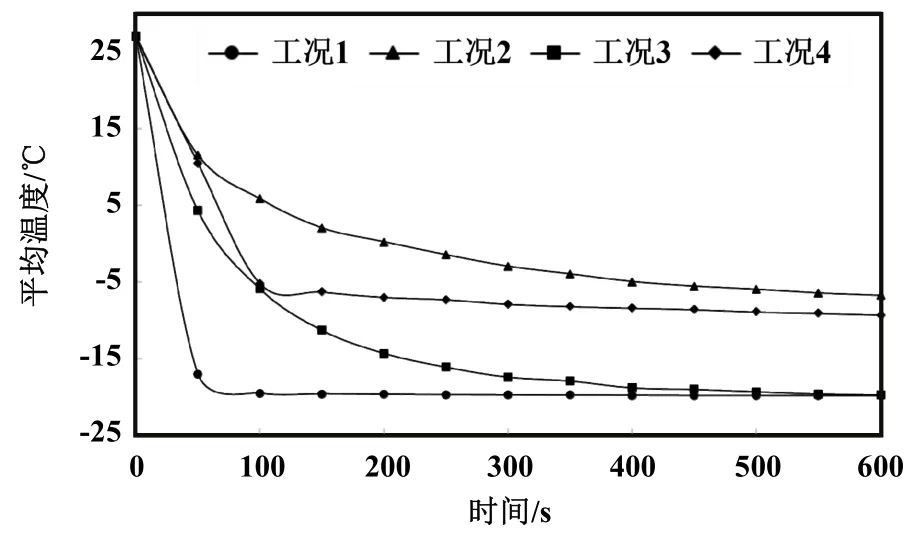
图5 工况1～4流场平均温度随时间的变化情况

图6 工况1～4流场温度标准差随时间的变化情况

从图6可以看出空载工况下具有一定温度差的气体来流一开始破坏了原有温度场的均匀性后，冷气对试验空间内初始气体进行置换，流场重新成为均匀场。无补偿空载工况在降温过程开始约 150 s后 σ≈0，而有补偿空载工况在降温过程开始至少600 s后才达到相同的温度标准差，整体温度场均匀性的回复过程落后于无补偿的空载工况。对比工况1和工况2的曲线可以发现，负载工况由于被试体的破坏，其温度场均匀性远不如空载工况，前者的温度标准差曲线峰值出现在降温过程开始约550 s。而有补偿的负载工况中，补偿气流不仅促进了降温过程的进行，同时也使得被试体与冷气流间的换热更加充分、彻底，因此工况 4的曲线峰值在 120 s左右即出现，整体趋势也极大地领先于工况2。

为了更好地观察被试体对冷气流的阻挡和粘滞作用，定义试验空间内两个定点A和B，其坐标分别为（1.9，3.1，4.4）和（6.2，0.9，4.4），在空间内的相对位置如图7所示。点A在被试体侧面附近，不受其阻挡，但受其粘滞力影响；点B在被试体下方一定距离处，受其粘滞力影响较小，主要受其阻挡。图8、9分别给出了点A、B在4种工况下温度及两点温度差随时间的变化趋势。

图7 定点A和B在试验空间中的相对位置

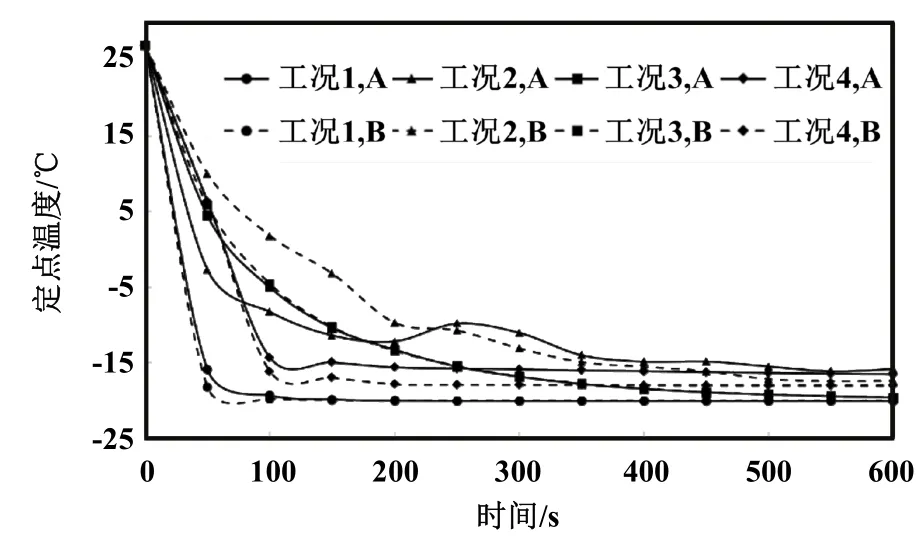
图8 定点A和B在不同工况中的温度变化趋势

定点A和B在工况1中的温度变化曲线基本重合，并与图5中平均温度曲线趋势大致相同，表明系统空载工况下流场均匀性较好。定点A和B在工况2中降温过程均受被试体影响而减缓，且有所波动。点B在降温过程初始阶段进度落后于点A，此时点B主要受被试体阻挡，未能充分换热；随着降温过程的进行，点B的冷却进度逐渐超过了点A，此时点A持续受到粘滞力影响，降温速率较慢，而冷空气已经在被试体下方富集，被试体的阻挡作用不再明显，点B的降温速率比较稳定。

定点A和B在工况3中的降温过程由于补偿气流的影响均明显减缓，但整体与工况3呈现相似的单调递减趋势。在工况4中由于补偿气流的修正效果，两者的降温过程相对于工况2不仅有所加速，而且因被试体影响而产生的波动也消失了。点A位于补偿气流出口附近，因此被试体对其粘滞力影响被明显抵消；另一方面，补偿气流加速了冷气体从侧面进入被试体下方，因此点B的冷却进度得到了明显提升。图9给出了点A和B在4种工况中的温度差变化趋势，可以更直观地观察到补偿气流体现在两点温度差上的修正效果。

图9 定点A和B在不同工况中的温度差变化趋势

3 结论

1）当试验系统负载有被试航天器时，由于被试件的热容以及其对气体来流的阻挡和粘滞作用，试验空间的降温过程进度减缓，温度均匀性恶化。在本文所设条件下，负载工况降温幅度在试验进行600 s时仅为空载工况的71%，温度标准差约为16，远大于空载工况（约为0）。

2）在负载工况下为试验空间提供垂直于原气体来流的补偿气流，以促进流场充分换热，修正其温度场均匀性。在本文所设条件下，有补偿工况的降温幅度在试验进行 100 s后约为无补偿工况的152%，且温度标准差曲线峰值出现在120 s左右，领先于无补偿工况（出现在约550 s）。可见补偿方案对负载工况有较为明显的效果。