低温余热用涡旋膨胀机的热力学特性研究及试验验证

彭斌，孙健

（兰州理工大学机电工程学院，甘肃兰州 730050）

0 引言

能源对于工业的发展至关重要。如今由于不可再生能源的大量消耗，人类正面临着能源缺乏的危机。然而，由于大多数不可再生能源利用效率和回收效率不高，造成了能源的极度浪费，大量的能源以中低品位（100 ℃～250 ℃）的形式排放到外界，加剧了能源的消耗。目前，有机朗肯循环系统就可以很好地解决这个问题。整个ORC系统的运行效率，决定了其能源回收利用效率的大小[1]。涡旋膨胀机是整个ORC系统最重要的组成部分，容积效率和等熵效率是用来衡量其性能的重要指标，因此提高涡旋膨胀机的容积效率和等熵效率是极其重要的。涡旋膨胀机工作过程中存在的吸、排气损失和质量以及热交换又极大地影响着容积效率和等熵效率。

在涡旋膨胀机的工作过程中，由于存在着吸排气损失、内泄漏以及热传递，导致涡旋膨胀机的理想与实际工作过程之间总是存在着一定的差异，因此对泄漏和传热等不可逆损失的研究有助于涡旋膨胀机的设计和优化[2-5]；通过对泄漏特性的研究发现，泄漏间隙对内泄漏有着重要的影响[6]，通过对泄漏线长度的计算发现径向泄漏线长度远大于切向泄漏线长度，径向泄漏引起的泄漏量也是最大的，因此径向泄漏对涡旋膨胀机性能的影响最大[7-10]；借助于试验才能进一步验证所建立的数学模型是否准确，进而提出一种新的设计方法来降低泄漏损失[11-13]。

在建立热力学模型时，可借助于温熵图来定性地表示热力学过程[14]；膨胀比、输出功率等都可作为涡旋膨胀机的基本热力学指标[15]；在建立热力学模型时大都基于变质量系统热力学，通过所建立的模型可数值模拟出泄漏量、质量、压力和温度等热力学参数与主轴转角之间的变化关系[16-17]；将热力学模型建立之后，在ORC系统中选用不同的工质，借助试验来验证所建立的热力学模型是否具有普适性[18-21]。

本文在已有研究的基础上，以空气为工质，在建立涡旋膨胀机的热力学模型时充分考虑了吸、排气损失、泄漏和热传递等不可逆损失对涡旋膨胀机性能的影响；通过分析理想膨胀和实际膨胀过程之间的差异，为涡旋膨胀机的设计和优化提供了一定的指导意义。

1 基本原理及性能参数

涡旋膨胀机在工作原理上属于容积式膨胀机，由于其构造特殊，相较于其他类型的膨胀机而言有着许多优点，因而被广泛应用于工业生产中。其工作原理如图1所示。当高温高压的工质流体通过进气口流入涡旋膨胀机时，工质流体开始推动动涡盘进行转动；当主轴转角达到膨胀起始角θ*时，腔体的容积不断地增大，气体开始不断地被膨胀；当主轴转角达到排气角θd时，流体的体积达到最大值，膨胀过程结束，排气过程开始；随着动涡盘的转动，排气腔不断减小，直到气体完全排出，排气过程结束。在涡旋膨胀机中每个工作过程并不是单一进行的，而是连续地在进行吸气、膨胀及排气。

本文研究所用涡旋膨胀机，其型线构成及腔体划分如图2所示，其设计参数如表1所示。其中，SS为吸气腔，E1、E2和E3分别为第一、第二和第三膨胀腔，dis为排气腔。

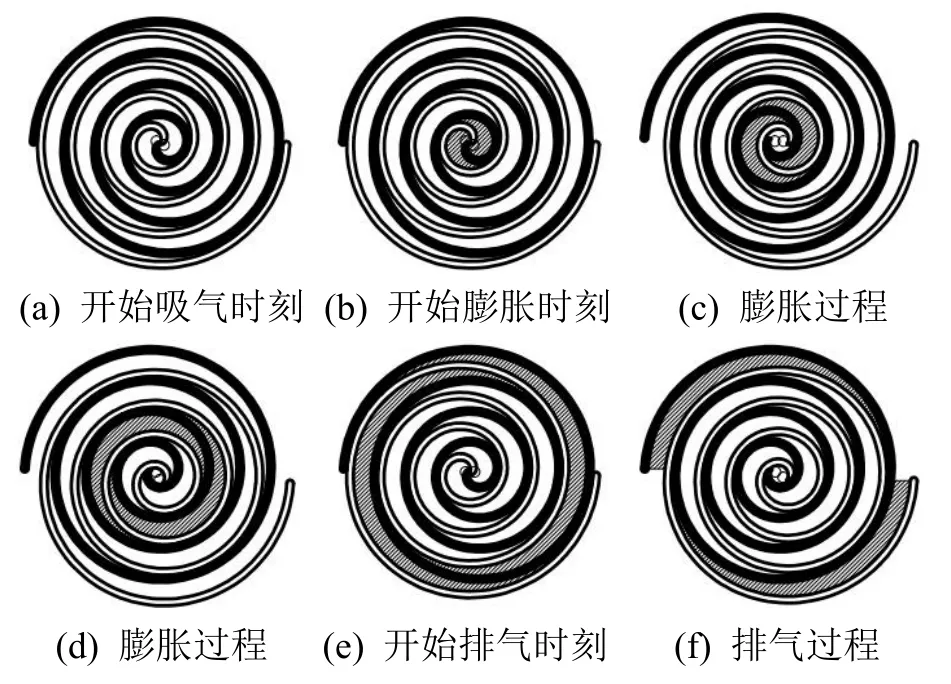
图1 涡旋膨胀机的工作原理

图2 涡旋膨胀机示意图及腔体划分

表1 涡旋膨胀机的基本参数

涡旋膨胀机的理想膨胀过程属于等熵过程，但是在实际工作过程中由于泄漏和热传递等因素的存在，实际等熵效率要小于理想等熵效率。在涡旋膨胀机中存在着两种形式的泄漏：内泄漏和外泄漏，其中内泄漏对涡旋膨胀机的工作效率影响最大；流体工质通过涡旋盘之间的缝隙进行质量交换，涡旋盘底部或顶部、涡旋齿与涡旋齿之间都存在着热交换。图3为泄漏和热交换示意图。

在涡旋膨胀机的内泄漏中，径向泄漏对其性能影响最大[7-9]，图4为径向泄漏通道示意图。

当曲轴转动θ时，控制容积的径向泄漏通道包括两部分：由高压腔泄入控制容积的通道和由控制容积泄出到低压腔的通道。

泄入和泄出控制容积的泄漏通道的长度计算如下式：

式中，φP1、φP2、φP3和φP4分别为在点P1、P2、P3和P4处的主轴转角，rad。

图3 泄漏和热交换示意图

图4 径向泄漏通道示意图

2 热力学模型的建立及计算

基于变质量系统热力学和单腔控制容积法，建立涡旋膨胀机的热力学数学模型。建立模型的前提是工质泄漏流动的形式为单相流动形式或均相流动形式。

图5 第i个膨胀腔的内泄漏模型

由于膨胀腔内的质量与泄漏有关，选取工作腔i为控制体。基于控制容积内质量守恒定律，控制体i内的质量为：

式中，min为从第i-1个工作腔泄入到控制体i的质量，g；mout为从控制体i泄出到第i+1个工作腔中的质量，g。

根据流入和流出控制容积的能量守恒，可以得到任意转角下控制容积的能量守恒方程：

式中，u为比热力学能，J/g；Q为热量，J；W为功，W；hin、hout分别为泄入和泄出控制容积的比焓。

在进行数值模拟分析时，所用的工质空气为理想气体，因此采用以下工质流体流过理想喷管的泄漏模型[22]。

径向泄漏：

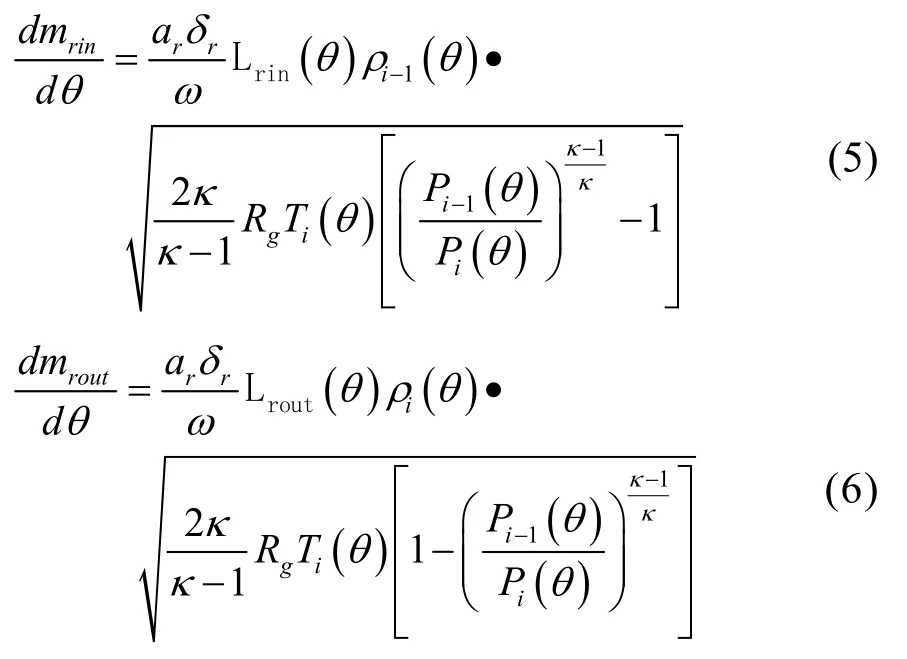
切向泄漏：

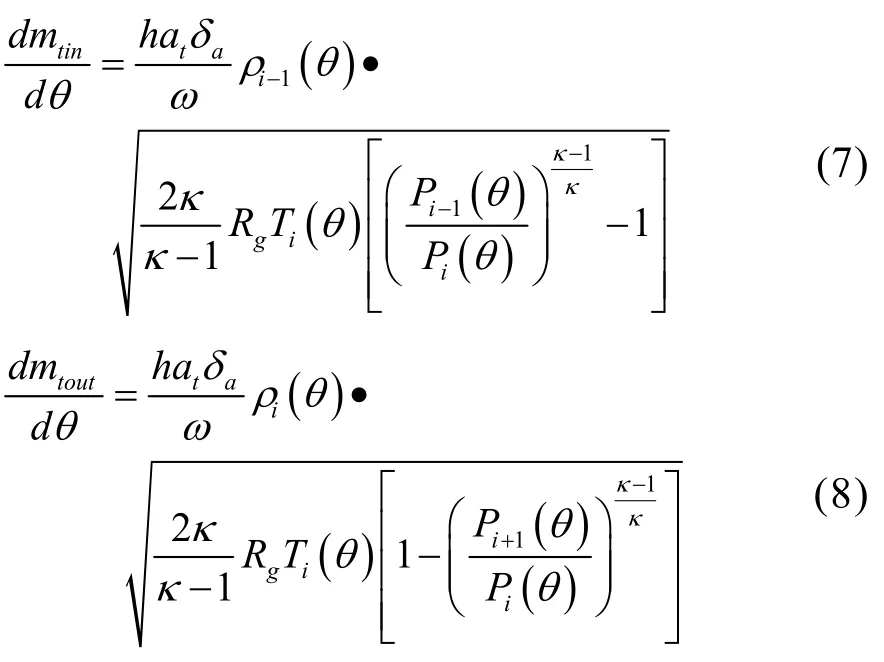
式中，ar、at为流量系数；δr、δa分别为径向和轴向间隙，mm；Rg为气体常数；Ti(θ )为主轴转角θ 时控制体 i的温度，℃；Pi-1(θ )、Pi(θ )、Pi+1(θ )分别为主轴转角θ 时第i-1、i、i+1个腔内的压力，MPa；ρi-1(θ )、ρi(θ )、ρi+1(θ )分别为主轴转角θ 时第 i-1、i、i+1个腔内的密度，g/mm3。

容积效率和等熵效率均是衡量涡旋膨胀机性能的重要指标，其计算公式分别如下：

式中，V标为标况下流体的体积流量，Vth为理论最小体积流量，其计算公式如下：

式中，ε*、ε 分别为理想和实际膨胀比，κ 为气体绝热指数。

3 计算结果与分析

在进行热力学模型的建立过程中，为了使所建立的模型与实际过程相符合，结合试验数据建立以下模拟条件：进口压力 Pin= 0.89 MPa，进口温度T = 298.15 K，主轴转速n = 2,500 r/min，涡旋膨胀机径向间隙δr= 0.05 mm，轴向间隙δa= 0.1 mm。

图6所示为在整个工作过程中，腔内压力随主轴转角变化的趋势。由于在进气口存在压力的节流作用，所以在进气阶段压力会有一个突变；随着主轴转角的不断变化，腔内的压力逐渐趋于平缓；在排气过程中由于排气口较大的缘故，压力损失并不明显；实际膨胀过程与理想膨胀过程相比，在吸气阶段两者相差较大。

图6 压力随主轴转角的变化

图7所示为工作腔容积随主轴转角的变化。结合图7(a)和图7(b)可知，泄漏对吸气腔和排气腔的容积没有太大的影响；但是在膨胀腔，尤其在第三膨胀腔内容积的变化最大，这是因为在第三膨胀腔径向泄漏线长度最长，所引起的泄漏损失也是最大的，所以增加密封条以减小轴向间隙是十分有必要的。

图7 容积随主轴转角的变化

图8所示为工作腔内质量随主轴转角的变化关系。在吸气结束时，腔内质量的实际值要小于理论值，这是因为进气口的节流作用使得实际进气压力小于理想进气压力；在膨胀过程中，由于泄漏的存在，腔内的质量在逐渐增加；在排气开始时，由于排气口较大，实际质量要高于理想质量，工质的质量随主轴转角的增大而逐渐减小。

图8 质量随主轴转角的变化

图 9所示为膨胀比与等熵效率之间的变化关系。随着膨胀比的逐渐增大，等熵效率随之也增大；但是当膨胀比增大到一定程度时，等熵效率反而有下降的趋势，在膨胀比大于4时理想等熵效率与实际等熵效率相差较大，这是因为随着进气压力的逐渐增大，气流的阻塞作用也越来越大，需要克服的阻力也越大。

图9 等熵效率与膨胀比

图 10所示为转速对容积效率的影响。随着转速的逐渐增大，容积效率也随之增大，这是因为在高转速时径向泄漏和切向泄漏逐渐降低的缘故；在实际膨胀过程中，容积效率在转速较低时增加较为明显，转速较高时增加变得缓慢；在相同转速下，容积效率的实际值要低于理想值，这是因为吸气孔口对吸入气体的节流作用变得更加明显。因此，增加密封装置和选取较大的转速都有助于提高涡旋膨胀机的容积效率。

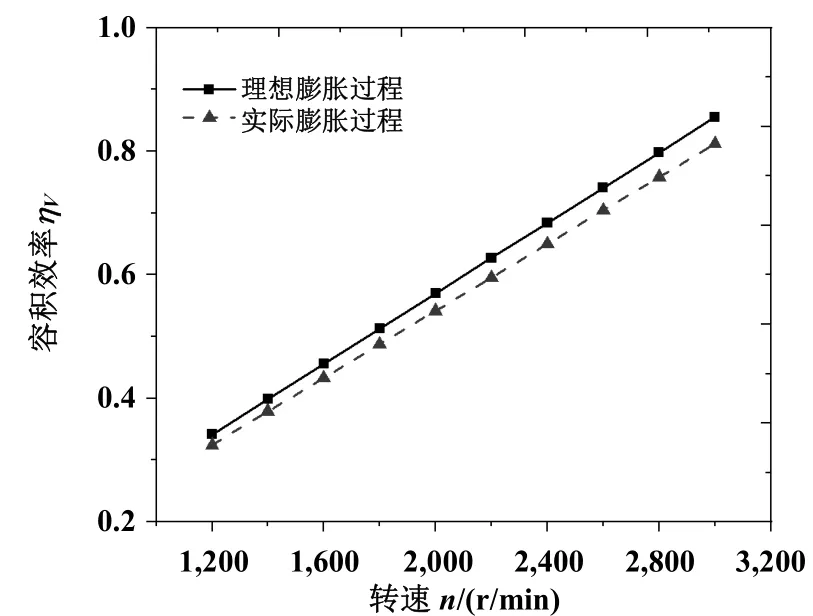
图10 容积效率随转速的变化

4 试验验证

为了验证所建立的热力学模型的准确性，本文搭建了以空气为工质的涡旋膨胀机试验性能测试平台，如图11所示。在图12中，通过对理论和试验输出功率之间的比较，发现功率的实际值与理论值存在着一定的偏差，偏差最大值为 322 W，最小值为16 W，误差在容许的范围之内，因此所建立的热力学模型能够反映出涡旋膨胀机的实际工作过程。

图11 试验测试平台

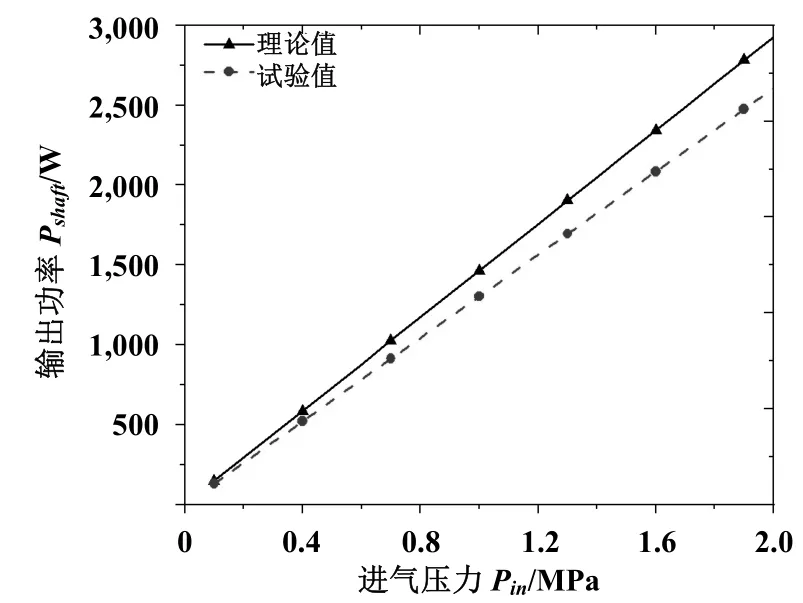
图12 输出功率与进气压力

5 结论

1）压力对涡旋膨胀机的性能有着直接的影响，在涡旋膨胀机工作腔内实际压力低于理想过程时的工作压力，在吸、排气时均存在着压力损失。

2）在工作腔内由于存在着质量交换，吸气结束时，腔内质量的实际值要低于理想值；在实际膨胀过程中质量随主轴转角的增大而增加，由于泄漏的存在，膨胀结束时，质量的实际值要高于理想值；由于泄漏的存在，吸气腔和排气腔内容积变化较小，在膨胀腔内容积的变化较大。

3）等熵效率与膨胀比呈正相关，理想过程时的等熵效率要高于实际膨胀过程的等熵效率；容积效率与转速呈正相关，在模拟条件下，容积效率的最大值为0.74。

4）通过搭建好的空气测试平台，测量了涡旋膨胀机的输出功率，对热力学模型的精确性和准确性进行了验证。