局部阴影下光伏阵列的MPPT综合优化

马永翔 王一君 闫群民 孙荔伟

摘  要： 针对光伏阵列在实际工作中被局部阴影遮挡，输出特性出现多个峰值点难以进行最大功率跟踪的问题，在分析研究局部阴影下光伏阵列输出特性的基础上，对传统电导增量法进行改进，提出一种模糊控制电导增量法。同时，将改进后的电导增量法同传统粒子群优化算法结合起来对光伏阵列进行联合控制，利用Matlab/Simulink平台搭建光伏阵列及其最大功率点跟踪的仿真模型，对该控制策略进行仿真分析，仿真结果表明所采用的方法能够实现MPPT的综合优化。

关键词： 局部阴影; 光伏阵列; MPPT; 混合控制; 综合优化; Matlab/Simulink; 比较分析

中图分类号： TN876?34; TM615                    文献标识码： A                    文章編号： 1004?373X（2019）11?0140?04

Abstract： Since the photovoltaic （PV） array is shadowed by local shadows in practical work， it is difficult to perform the maximum power point tracking （MPPT） for multiple peak points appeared in output characteristics. On the basis of analyzing the output characteristics of PV array in partial shadow， the traditional conductance increment method is improved， and a fuzzy control conductance increment method is proposed. The improved conductance increment method is combined with traditional particle swarm optimization algorithm to perform the joint control for PV array. A simulation model of PV array and maximum power point tracking was built with Matlab/Simulink platform. The simulation analysis is carried out for the control strategy. The simulation results show that the adopted method can realize the synthetic optimization of MPPT.

Keywords： partial shadow; PV array; MPPT; hybrid control; synthetic optimization; Matlab/Simulink; comparative analysis

0  引  言

太阳能由于其清洁无污染的特性成为新能源开发和利用的主要对象之一，随着智能电网的快速发展，光伏发电并网的可靠性得到提高，促进了光伏产业的快速发展和进步[1]。光伏阵列由光伏电池串并联链接组成，光伏电池受光照强度的影响巨大，当一组光伏阵列局部处于阴影下时，输出特性曲线会出现多峰现象[1]，使光伏发电效率降低，降低了能源利用率。传统的最大功率跟踪，如电导增量法、恒定电压法、扰动观察法等[2?5]受到局部峰值的影响，难以找到最大功率点，无法实现最大功率跟踪的目的。针对这一问题，文献[6]利用空间向量法对光伏阵列的布局结构进行优化，通过优化光伏阵列的排列方式优化最大功率跟踪，虽然能够有效提高最大功率点跟踪精度，但是计算结构复杂，必然会延长控制时间。文献[7]提出一种混合蛙跳算法，虽然能够有效提高多峰值输出的最大功率跟踪效率，但是增加了控制难度。文献[8]采用模糊控制进行最大功率点跟踪控制，所采用的控制结构复杂，难以提高控制效率。

本文在分析研究局部阴影下光伏阵列输出特性的基础上，对传统的电导增量法进行模糊控制，并结合粒子群优化算法对光伏阵列进行联合控制，同时在Matlab/Simulink平台上搭建了光伏发电系统的仿真模型，对所提出的方法进行仿真分析，得出该方法能够较好地实现最大功率跟踪的结论。

1  局部阴影下光伏阵列的输出特性

光伏电池通过光生伏特效应将光能转化成电能，由于单块光伏电池所产生的电压较小，所以在实际应用中，必须将光伏电池通过串并联组成光伏阵列。但是，由于云层、树木、房屋的遮挡，光伏阵列所受光照强度不均匀，使得整个阵列的输出特性曲线出现多个峰值，传统最大功率跟踪的方法就难以实现最大功率跟踪，降低了光伏阵列的发电效率。严重情况下，会使得局部阴影下的光伏电池受反向电流影响而产生热斑效应，损坏光伏电池器件。

光伏阵列所接受的整体光照强度不同，所受到阴影的影响程度也不同。定义[a]为阴影处的光照强度和无阴影遮挡处的光照强度之比，通常[a]越接近1，光伏阵列所受到的局部阴影的影响越小，反之越大。而且，阴影遮挡的面积以及遮挡区域不同，对光伏阵列的影响也不同。所以，这就造成在局部阴影下光伏阵列的输出特性具有多峰值、不稳定的特点，增大了最大功率跟踪的难度。

光伏电池的主体结构是一个PN结结构，其特性和二极管类似[9]。实验中，针对不同型号的光伏电池，所对应的额定参数也不同。光伏电池的主要参数包括短路电流[Is]，开路电压[UOC]，最大功率电压[Um]和最大功率电流[Im]。其等效电路图如图1所示。

图1  光伏电池等效电路

光伏阵列在实际应用过程中，工作在局部阴影条件下时，输出特性曲线明显出现多峰值现象，使得光伏阵列的总体输出功率降低，减小了光伏发电效率，同时也增加了最大功率的跟踪难度。

2  最大功率点跟踪综合控制策略

2.1  粒子群优化算法

粒子群算法（PSO）属于进化算法的一种，它可以利用当前最优值得到全局最优的结果。利用粒子群算法对光伏发电进行最高功率点的跟踪，具有速度快、算法简洁的优点。传统的粒子群算法在复杂条件下对光伏阵列进行最大功率点跟踪，粒子群寻优往往会陷入局部最优点，使跟踪准确率降低。本文采用文献[10]提出的方法对传统的粒子群算法进行优化，除去算法中的随机因素和限制峰值之间的速度因子，快速扫描全局，定位可能存在的最优位置，锁定最优区域。这种方法的优点在于能够快速锁定全局最优区域，提高运算速度，降低控制难度，在一定程度上提高了粒子群算法的精确性。

2.2  模糊控制电导增量法

传统的电导增量法虽然能够使光伏电池的输出电压随着日照强度稳定变化，但其控制复杂，对步长控制要求高，在一定程度上影响了算法运行的精度和速度。模糊控制电导增量法是在传统电导增量法的基础上加入模糊逻辑语言，提高控制速度和精度。该方法的主要步骤如下：

1） 设定模糊子集与语言变量：将上一时刻的占空比扰动值[αt-1]与本时刻的功率差与电压差的比值[Δβt=dpdv]作为输入语言，将本时刻的占空比[αt]作为输出语言。[αt]和[Δβt]的模糊子集为：

当[Δβt]的误差较小时，选取分辨率较大的隶属度函数进行控制，当[Δβt]的误差较大时，选取分辨率较小的隶属度函数进行控制。式（4）中，[b]的取值直接决定隶属度函数的形状和误差，应根据实际控制要求进行设定。

3） 设定模糊逻辑的原则：当跟踪点距离最大功率点较远时，应该增大步长;反之，应该减小步长。当外界环境发生变化，控制系统也要做出相应的调整。

2.3  混合控制策略

混合控制策略的原理是先利用粒子群算法进行全局寻优，找到最大功率点所在的近似区域，然后利用模糊控制电导增量法对锁定区域进行最大功率跟踪，这样，既避免了粒子群算法因为陷入局部最优而出现跟踪失准，又可以提高跟踪效率与速度，同时能够使光伏电池的输出电压随日照强度平稳变化，保障输出电压的稳定性，提高跟踪精度。最大功率跟踪控制原理如图2所示。

图2  最大功率跟踪原理

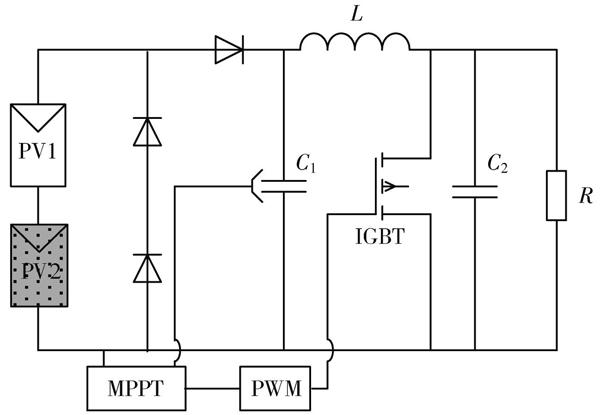
最大功率跟踪控制器将光伏电池的输出电压和电流作为输入量，然后通过混合控制算法对最大功率点进行跟踪，再通过PWM调制控制直流升压单元中IGBT的占空比，从而控制输出电压工作在最大功率点。

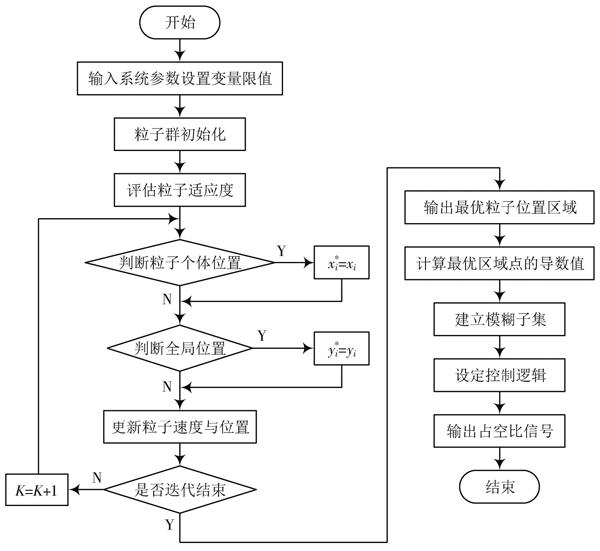
混合控制策略（见图3）主要包含两个步骤：

1） 利用粒子群算法对光伏阵列的输出特性曲线进行全局寻优，设定粒子群的初始参数，评估粒子适应度，通过判断粒子个体位置和全局位置来更新粒子位置，得到寻优解，确定初始占空比和最优区域。

2） 利用模糊控制电导增量法进行局部寻优，设定模糊子集与逻辑语言，编写控制规则，调整相应参数和比例因子，输出占空比信号，控制DC?DC电路使光伏阵列工作在最大功率点。

图3  混合控制流程图

3  仿真分析

根据图2，通过Matlab/Simulink软件搭建系统的仿真模型。光伏阵列由6个光伏电池模型组成，温度设定为标准温度[T=]25 ℃，光照强度分别为1 000 W/m2，1 000 W/m2，1 000 W/m2，800 W/m2，600 W/m2，400 W/m2。粒子群優化算法初始参数：粒子种群数为30，维数为2，粒子运行速度分别为1和0.3，学习因子为2，迭代次数为30。

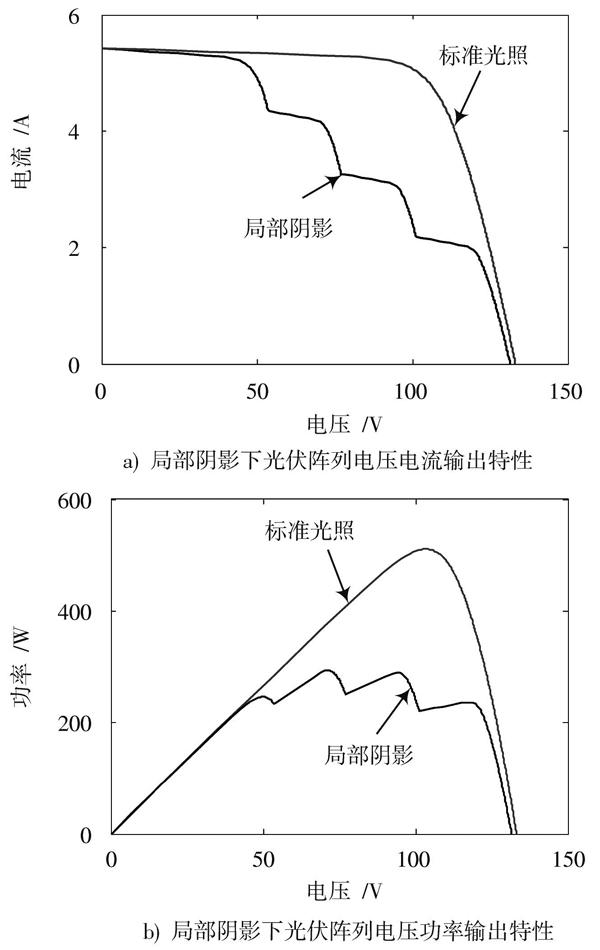
局部阴影下的光伏阵列输出特性如图4所示，从图中可以得出，光伏阵列在不均匀的光照强度下，输出特性曲线出现多峰现象，全局的最大功率要比在标准光照强度[S=]1 000 W/m2时的最大功率小，而且出现多个局部最大功率点。其中，全局最大功率[Pm=]326.4 W，粒子群优化算法结果：[Pm=]313.6 W，对应电压[Um=]73.2 V。

图4  局部阴影下光伏阵列输出特性

利用模糊控制对电导增量法进行改进，能够提高算法速度和精确度，仿真结果如图5所示。

图5a）和图5b）分别是利用粒子群算法和模糊控制电导增量法下，光伏阵列功率输出波形图，从图中可以得出，模糊控制电导增量法的收敛性、算法运行时间、精确性要强于粒子群优化算法。采用混合算法仿真波形图如图6所示。

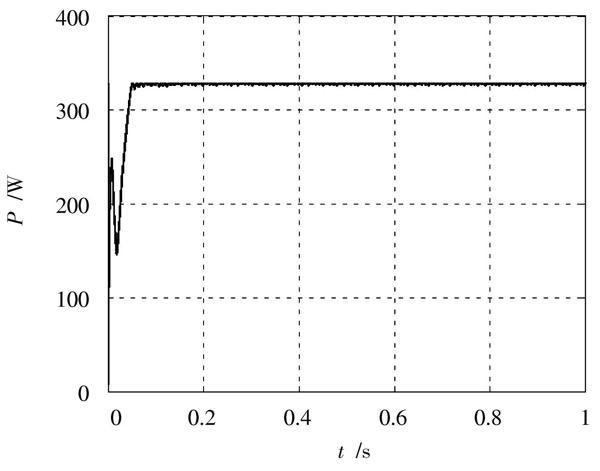
由图6可得，采用粒子群优化算法和模糊控制电导增量法相结合的混合算法对光伏阵列进行最大功率点跟踪，跟踪精度更高，所需要时间更短。在该方法下，光伏阵列输出功率为324.5 W，更加接近理论计算值，所以，所采用的方法对于最大功率跟踪具有更好的效果。

4  结  论

光伏阵列工作在局域阴影下，其输出特性曲线会出现多个峰值，难以进行准确的最大功率点跟踪，使光伏阵列的运行效率降低。本文针对这一问题对光伏阵列最大功率点跟踪控制进行如下改进：

1） 在传统的电导增量法基础上采用模糊控制，简化了控制步骤，在提高控制效率的同时提高了算法的收敛性和准确性。

图5  粒子群优化算法和模糊控制电导

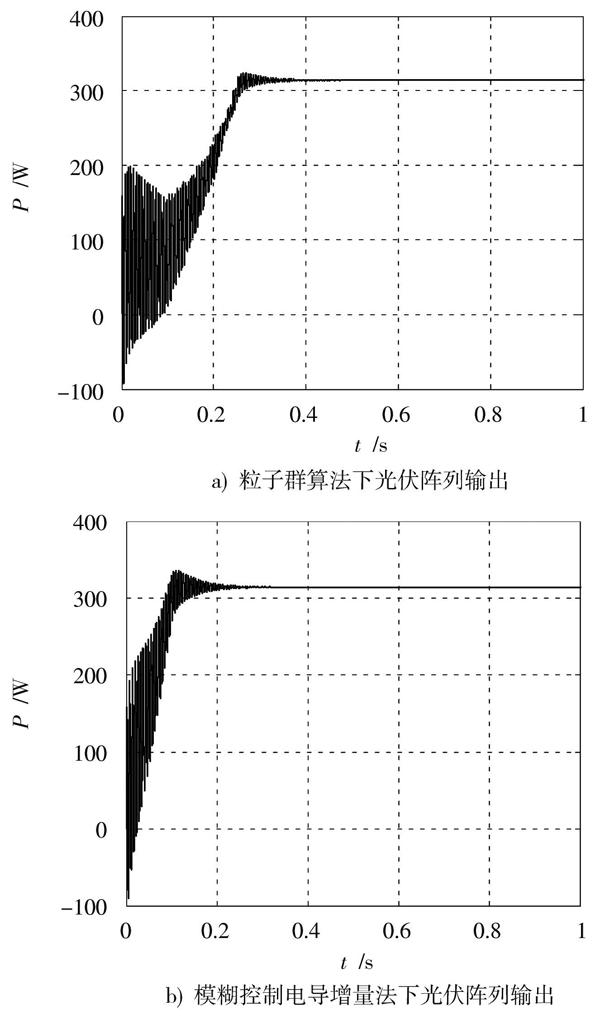
图6  混合算法下光伏阵列输出特性

2） 将粒子群优化算法同模糊控制电导增量法结合起来，对光伏阵列进行联合控制，进一步提高了光伏阵列工作在局部阴影下最大功率跟踪的准确性，而且降低了跟踪算法的运行时间，提高了发电系统的运行效率。

3） 利用Matlab/Simulink平台搭建光伏发电系统仿真模型，对所提出的控制方法进行仿真验证，结果表明模糊控制下的电导增量法比粒子群优化算法具有更好的收敛性，运算效率更高，而粒子群优化算法和模糊控制电导增量法的联合控制方法能够进一步提高控制效率。

参考文献

[1] 陈树勇，宋书芳，李兰欣，等.智能电网技术综述[J].电网技术，2009，33（8）：1?7.

CHEN Shuyong， SONG Shufang， LI Lanxin， et al. Survey on smart grid technology [J]. Power system technology， 2009， 33（8）： 1?7.

[2] 卞海红，徐青山，高山，等.考虑随机阴影影响的光伏阵列失配运行特性[J].电工技术学报，2010，25（6）：104?109.

BIAN Haihong， XU Qingshan， GAO Shan， et al. Operation mismatches of photovoltaic array considering random shadows [J]. Transactions of China electrotechnical society， 2010， 25（6）： 104?109.

[3] LIU F， DUAN S， LIU F， et al. A variable step size INC MPPT method for PV systems [J]. IEEE transactions on industrial electronics， 2008， 55（7）： 2622?2628.

[4] 周德佳，赵争鸣，袁立强，等.具有改进最大功率跟踪算法的光伏并网控制系统及其实现[J].中国电机工程学报，2008，28（31）：94?100.

ZHOU Dejia， ZHAO Zhengming， YUAN Liqiang， et al. Implementation of a photovoltaic grid?connected system based on improved maximum power point tracking [J]. Proceedings of the CSEE， 2008， 28（31）： 94?100.

[5] 杨永恒，周克亮.光伏电池建模及MPPT控制策略[J].电工技术学报，2011，26（1）：229?234.

YANG Yongheng， ZHOU Keliang. Photovoltaic battery mode?ling and MPPT control strategy [J]. Transactions of China electrotechnical society， 2011， 26（1）： 229?234.

[6] ABDELSALAM A K， MASSOUD A M， AHMED S， et al. High?performance adaptive perturb and observe MPPT technique for photovoltaic?based microgrids [J]. IEEE transactions on power electronics， 2011， 26（4）： 1010?1021.

[7] 周元贵，陈启卷，何昌炎，等.局部阴影下光伏阵列建模及多峰值MPPT控制[J].太陽能学报，2016，37（10）：2484?2490.

ZHOU Yuangui， CHEN Qijuan， HE Changyan， et al. Model of PV array under partial shading and MPPT control of multi?peak characteristics [J]. Acta energiae solaris sinica， 2016， 37（10）： 2484?2490.

[8] 刘立群，王志新，张华强.部分遮蔽光伏发电系统模糊免疫MPPT控制[J].电力自动化设备，2010，30（7）：96?99.

LIU Liqun， WANG Zhixin， ZHANG Huaqiang. Fuzzy?immune MPPT control of PV generation system under partial shade condition [J]. Electric power automation equipment， 2010， 30（7）： 96?99.

[9] 廖志凌，阮新波.任意光强和温度下的硅太阳电池非线性工程简化数学模型[J].太阳能学报，2009，30（4）：430?435.

LIAO Zhiling， RUAN Xinbo. Non?linear engineering simplification model of silicon solar cells in arbitrary solar radiation and temperature [J]. Acta energiae solaris sinica， 2009， 30（4）： 430?435.

[10] 胡克用，胥芳，艾青林，等.适用于光伏多峰功率跟踪的改进型粒子群优化算法[J].西安交通大学学报，2015，49（4）：140?148.

HU Keyong， XU Fang， AI Qinglin， et al. Improved particle swarm optimization for photovoltaic multi?peak power tracking [J]. Journal of Xian Jiaotong University， 2015， 49（4）： 140?148.

[11] 李志刚，田盛.局部阴影下光伏阵列结构优化[J].太阳能学报，2016，37（12）：2999?3004.

LI Zhigang， TIAN Sheng. Structure optimization of PV array under partial shade [J]. Acta energiae solaris sinica， 2016， 37（12）： 2999?3004.