一种在NLOS环境下应用于NB?IoT系统的组合定位算法
2019-06-19崔理伟林基明符杰林刘锦玲
崔理伟 林基明 符杰林 刘锦玲

摘 要: 传统非视距(NLOS)误差下无线定位的TDOA算法通常是减弱NLOS误差影响或直接提取LOS测量值,对于窄带物联网(NB?IoT)需要解决LOS与NLOS传输并存下的定位精度问题。文中采用最小二乘法对NLOS和LOS传播进行鉴别,然后对NLOS下的TDOA值进行优化处理。在此前提下,提出一种组合定位的算法,采用Taylor级数展开法计算LOS传输情况,用CHAN算法计算NLOS传输情况,再通过组合定位得到定位结果。仿真结果表明,改进后算法在NLOS的信道环境下的定位性能明显提高。
关键词: OTDOA; TDOA误差鉴别; NLOS误差优化; Taylor级数展开法; CHAN算法; 组合定位
中图分类号: TN921?34 文献标识码: A 文章编号: 1004?373X(2019)11?0001?06
Abstract: The traditional wireless location TDOA (time difference of arrive) algorithm with non?line?of?sight (NLOS) error is usually used to weaken the influence of NLOS error or directly extract the LOS measurement values. For NB?IoT, the positioning accuracy at the coexistence of LOS and NLOS transmission needs to be improved. Therefore, the least square method is used to identify the propagation of NLOS and LOS, and then optimize the TDOA values at NLOS. Under this premise, a combination positioning algorithm is proposed, whose basic thoughts are to use the Taylor series expansion method to calculate the LOS transmission delay, adopt the CHAN algorithm to calculate the NLOS transmission delay, and obtain the positioning result by means of combination positioning. The simulation results show that the proposed algorithm after perfection can improve the localization performance in NLOS channel environment obviously.
Keywords: OTDOA; TDOA error identification; NLOS error optimization; Taylor series expansion method; CHAN algorithm; combination location
0 引 言
随着移动物联网的发展与应用,“万物互联”将成为未来物联网的必然趋势,特别是低功耗广域网络(Low Power Wide Area Network,LPWAN)是专为低带宽、低功耗、远距离、大量连接的物联网应用而设计,必然成为未来5G部署的重要分支[1]。对于这种情况,华为、高通联合提出NB?CIoT技术,而爱立信、中兴、诺基亚等廠商联合提出NB?LTE技术,最终经过激烈地竞争和讨论,融合形成了NB?IoT技术。运营商和政府对LPWAN市场表现出极高的需求,物联网应用中的重要部分预计将需要定位服务,大大拓宽了窄带物联网定位的应用空间。
由于全球导航卫星系统(GNSS)芯片的功率和成本过高等问题,使得GNSS芯片并不适用于巨量连接的大型物联网。此外,NB?IoT设备很可能处于极端覆盖环境的位置(例如室内,管道中或地下),这又需要终端设备针对NLOS误差有良好性能的定位算法。为了能最大限度地保证NB?IoT发挥其本身高覆盖、低功耗和低成本等优势,3GPP工作组在RAN#72会议中批准了NB?IoT定位增强功能的工作项目,并同意引入支持UTDOA(Uplink Time Difference of Arrival)或OTDOA(Observed Time Difference of Arrival)的定位功能。因此,各大运营商和通信公司在RAN#86会议上就定位准确性、UE复杂度、UE功耗等进行了讨论。
目前,已经有一些研究人员提出能应用于NB?IoT的TDOA算法,其中大部分是针对NLOS误差进行优化。
在文献[1]中提出一个在嘈杂环境中的无线传感器网络移动定位方法。这种方法的重要特点是不需要知道非视距误差的参数,其关键技术是NLOS的识别和缓解。文献[2?3]中类似地采用贝叶斯序列测试方法来识别信标节点的传播情况,不过文献[2]根据确定的测量条件,利用卡尔曼滤波器(MKF)调整测量噪声协方差和预测协方差来减轻NLOS效应,文献[3]通过减去NLOS误差的平均值来校正包含NLOS误差的NLOS测量,以减轻NLOS传播的影响。文献[4]通过联合估计源位置和传输时间来实际制定RLS方程,RLS方程通过应用二阶锥松弛(SOCR)技术,解决RLS问题中未知数相互耦合的问题,最终得到定位坐标。文献[5?6]采用类似的误差分布转换法消除NLOS引起的超量时延影响,改善了非视距下的CHAN算法性能,最终解算得到定位坐标。文献[7?8]提出一种基于残差加权(RWGH)算法的降低非视距误差的改进方法,这种方法的基本思想是逐渐消除非视距传输情况,然后在LOS传播环境中进行定位。
然而,上述文献所提出的方法均出于移动定位的考虑,将信道情况简化为单一的NLOS或者LOS环境,然后进行优化和定位,不可避免地损失了一部分的信道数据,降低了实际信道下的定位精度。
本文基于NB?IoT的部署特点,在NLOS和LOS互相掺杂的实际信道下,对传播情况进行鉴别,最大程度利用信号的全部TOA数据进行定位,从而提高在实际NLOS信道下的定位精度。
1 NB?IoT的定位模型
对于NB?IoT的TDOA方案,各大通信公司讨论的结论是:在UE复杂度以及UE协议实现和内存要求上,UTDOA具有优势;在网络硬件要求和UE容量上OTDOA具有一定的优势;而在定位精度、网络同步等方面,两者性能相似。在讨论中支持OTDOA定位方案的公司认为,UTDOA需要使用窄带物理随机接入信道(NPRACH)来支持定位,由于NB?IoT的共享信道资源有限且干扰严重,系统的可扩展性受到上行信号序列和资源数量的限制,而OTDOA没有此类容量的限制。此外,大规模部署的NB?IoT设备预计具有较长的生命周期,很可能超出现有网络演进到5G环境,OTDOA的信号测量处理结构也能够与5G定位具有协同作用,这样有利于将来5G标准的移动边缘计算(MEC)实现。而在将来,UTDOA定位方案很可能无法应对大规模的物联网终端部署情况,所以NB?IoT系统发展OTDOA定位将是必然的趋势。
在此简要地介绍3GPP开发的OTDOA的初步架构和协议。更详细的协议案例可以参考相关的3GPP技术规范来了解更多细节。在OTDOA中,UE测量从多个小区接收的定位参考信号(PRS)的到达时间(TOA),并从测量TOA中减去参考小区的TOA以形成参考信号时差(RSTD),测量到达时间差(TDOA)[9]。
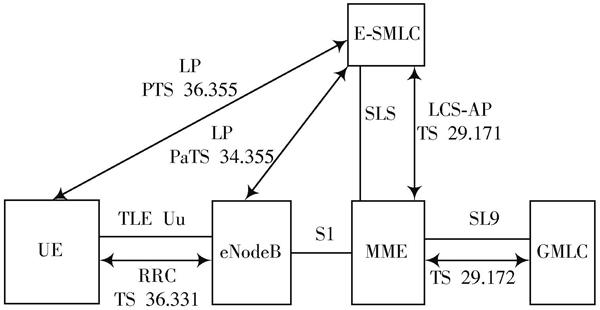
LTE中的定位由图1所示的架构支持。架构下的典型定位信令流如下:首先,由移动性管理实体(MME)主动发起,或者MME接收到来自UE或网关移动定位中心(GMLC,GMLC是外部LBS客户端与之通信的第一个节点)的位置服务请求;然后,MME向定位服务器(即演进服务移动定位中心(E?SMLC))发送定位请求。E?SMLC处理请求,与UE通信,并请求RSTD测量。在从UE接收到RSTD测量值时,E?SMLC估计出UE的位置并将结果发送回MME,而MME可以根据需要进一步将结果转发给UE或GMLC。从这一部分可以看出,为尽量减少UE的负担,在整个系统中由E?SMLC进行数据的处理和计算,这样会在一定程度上降低实时定位的响应速度,但能使系统接受更复杂的算法,从而提高定位精度。

图1 LTE定位结构图
NB?IoT的定位服务基本采用蜂窝网的TDOA定位方式,TDOA定位是一种基于信号传播时延的方法,而TDOA的基本思路是对信号传播时延进行测量。由此假设时间点[T0]时有两个信号分别从基站[i]和基站[j]发射出来。在接收端,MT在时间点[Ti]和[Tj]分别接收到来自于基站[i]和基站[j]的信号[10]。相应的传播距离差计算公式为:
式中:[Ti,j]就是测量的TOA;[TNLOS]是电磁波的视距传播时间;[τ]是测量偏差,这个偏差被认为是一个高斯随机变量,平均值为零,标准差很小。[TNLOS]为非视距传播引起的附加时延误差,其只与电磁波的传播环境有关。对NLOS引起的超量时延进行统计分析,[TNLOS]均值为[μNLOS],方差为[δ2NLOS]。但在不同的信道环境中,[TNLOS]的概率密度分布可能是指数、均匀、高斯或delta统计分布。
在实际的定位环境中,TOA的测量值误差很难真正地服从零均值的高斯分布,通常只有MS与BS之间电波能够LOS传播,即要求无障碍物阻隔的情况下才能做到。但在大多数的蜂窝网小区中,受到多径效应的影响,NLOS的传播及多址干扰等因素造成的TDOA误差才是定位误差的主要来源。通常运营商在进行蜂窝网的基站选址时,为了确保用户的信号稳定会布设大量的基站收发台,以确保不会出现信号盲区。因此,对于NB?IoT这种经常应用于复杂环境的终端来说,接收到的TOA信号同时包含LOS和NLOS误差。在这种情况下,使用传统的只针对LOS或NLOS误差的算法,必然会损失一部分精度。本文将LOS和NLOS下的测量数据进行鉴别分离后,再用组合定位法进行目标定位,以此运用所有数据来提高定位精度。
2 NLOS误差鉴别和优化
实际的定位系统中,TOA的测量误差主要来自测量设备及信号传播环境影响,设参与定位的基站为[M]([M>]3)個,记为1,2,…,[M],所有这些[M]个距离测量都被分组,将有[N]个不同的距离测量组合:
距离测量的组合可以命名为[Skk=1,2,…,N],对NLOS误差的鉴别过程描述如下:
1) 从全站选取[M]个基站,组合的个数为[M1=CMM=1]。采用最小二乘法计算移动台坐标向量的中间值[Xk1],即可得到:
式中:[di]是基站和移动台之间的测量距离;[Xi]是基站的坐标;[S1]是[M]个基站的组合;[Xk1]是通过使用[M]个基站的坐标估计的移动台的坐标。进一步推导得到:[Res1Xk1,S1=Res1Xk1,S1M1=Res1Xk1,S1CMM ] (5)
2) 从全站选择[M-1]个基站,例如选择1,2,…,[M-1]个基站,组合的个数为[M2=CM-1M=M],重复以上步骤即可得到:
式中:[S2]是[M-1]个基站的组合;[Xk2]是通过使用[M-1]个基站的坐标估计的移动台的坐标。
3) 比较Res1和Res2。如果Res1
4) 将[M]替换为[M-1],[M-2],…,4([M>3]),重复步骤1)~步骤3)以鉴别各基站的传播路径,直到当选择不同的基站组合时Res1不改变,说明所选基站的传播路径是LOS传播。
至此,完成了对整个基站的传播路径的鉴别。
在NLOS环境下附加时延通常可以认为由功率时延分布产生,在此类无线信道的仿真中,最常用的是由Ericsson的移动定位研究组提出的T1P1模型,也称为COST259模型。在这个模型中通常可以认为服从指数分布,其概率密度函数为:
式中:[τrms]为由信道环境决定的均方根时延扩展,在都市类环境中[τrms]与平均超量时延类似,即[μ][∶][τrms]=1[∶]1,可以认为[τrms]是服从对数正态分布的随机变量,因此:
式中:[d]是MS与BS之间的距离;[Ti]为[Trms]在[di=1] km时的中值;[ε]为0.5~1之间的一个常数;[ξ]为服从0均值的对数正态分布的随机变量,标准差[δξ]为4~6 dB(即[10log ξ]是零均值、标准差为[δξ]的服从正态分布的随机变量)。
不同环境下的具体参数由T1P1模型中的Greenstein模型给出,如表1所
表1 不同信道环境下的Greenstein模型参数

式中:[n′i,1]服从[N]([0,δ2ni,1+δ2NLOSi,1])分布。如此就使误差分布符合CHAN算法的ML估计条件,然后就可以将CHAN算法应用于优化后的NLOS测量值,进行MS的位置估算。
3 组合定位TDOA算法概述
通常在TDOA定位中,当基站数大于3时,将会产生一组冗余方程。为了得到更精确的定位坐标,特别是当考虑到测量的方差与协方差时,需要对定位方程进行算法优化。因此本文选择递归的Taylor级数展开法和非递归的CHAN算法。
根据TDOA定位原理,可以设已知基站[i]坐标为([xi,yi]),而移动台MS的坐标为([x,y]),因此MS到基站[i]的距離为:
将[Ri],[x,y]都看作未知数,然后在基站数大于4时,至少能得到一组冗余方程,求解此方程组就能得到定位结果。目前,有多种方法用于求解这一类的线性方程组,如FANG,CHAN,Taylor,SX,SI,DAC等,其中CHAN算法和Taylor级数展开法是最常使用的两种算法[11]。
Taylor级数法通过Taylor级数展开法对方程组(15)进行线性化,然后采用迭代法求解线性方程组。迭代方法以猜测初始值开始,通过确定局部线性最小二乘(LS)解决方案来改进每次迭代的估计。由此Taylor级数可以提供准确的结果。更具体地说,即该方法利用一组TDOA估计,以未知MT的移动位置[(x,y)]的初始猜测[(x0,y0)]开始,并且以此计算位置估计的偏差。公式表明Taylor级数展开法能得到较准确的计算结果,还能利用冗余的测量值提高定位的精度。但在实际应用中,尤其是NLOS误差的影响下,MT的初始位置很难确定,因而导致Taylor级数展开法有可能得不到收敛的结果,因此将LOS测量值使用Taylor级数展开法求解定位,可以有效避免这种情况的发生。
CHAN氏算法是一种具有解析表达式解(Closed Form Solution)的非递归双曲线方程算法。该算法的特点是计算量小,在噪声服从高斯分布的环境下,定位精度高。但在非视距环境下,CHAN氏算法的定位精度显著下降[10]。在4个以上基站的CHAN算法上,当TDOA距离差误差较小时,该算法的性能能达到CRLB(克拉美罗下界),但是整个算法的推导都是基于测量噪声服从零均值高斯随机分布这个前提,因此在实际的NLOS环境下,信道的环境误差会较大,CHAN算法的性能将受到较大影响,因此本文之前对NLOS误差进行了一定程度的优化,使优化后的NLOS测量值尽量满足CHAN算法的定位条件。
由前面的描述可知,在实际的NLOS环境下CHAN算法定位性能大受影响,而Taylor算法甚至可能得不到定位结果。因此,直接使用这两种算法进行组合定位并不是一个好想法。为了达到在NLOS环境下的定位精度要求,需要将CHAN算法和Taylor算法进行分离计算然后再进行加权,进而得到一种适用于NLOS环境的组合算法。
一般情况下,两种算法估计器的组合是使用CHAN算法估计器来初始化Taylor算法估计器,即直接通过CHAN算法进行测量数据的初始定位,然后将其作为Taylor级数展开法的初始值。但是,使用CHAN算法的估计值来作为Taylor算法的初值,尽管Taylor估计器的结果将略微改善,但是这种算法的有效性是值得怀疑的,因为它违反了数据的独立性假设。所以,本文将CHAN算法和Taylor级数展开法分别应用于NLOS和LOS测量数据得到初步估计值,然后进行简化的残差加权计算,得到全新的定位估计。
假设TDOA测量值数目为[N],[Xi]和[Xj]则分别为该算法参与定位的基站坐标,[X0]是服务基站坐标,由Taylor和CHAN算法得到的初始定位坐标为[Xt]和[Xc],[Zt]和[Zc]分别是Taylor和CHAN算法的权系数:
4 仿真描述、结果及分析
本文的信道仿真采用T1P1模型,仿真条件如下:小区半径[R=]3 000 m,基站数(BS)为7。假设在LOS情况下,测量误差服从零均值理想高斯分布,标准差[σ]分别取值为30 μs,45 μs,60 μs,75 μs,90 μs,105 μs,120 μs,135 μs,150 μs。对于初始的真实移动位置,增加了由零均值和给定标准偏差的高斯噪声产生的随机扰动,在此基础上按照COST259模型来增加NLOS误差,每次仿真运行的次数为10 000次,本文采用定位结果的均方根误差来表示定位精度。其中,均方根误差(RMSE)的表达式近似为:
为了简化终端的复杂度和降低终端功耗,NB?IoT被设计应用于低速率、弱移动的应用场景(如智能抄表、智能停车),同时NB?IoT不支持连接态的移动管理,并直接使用小区搜索和同步代替了切换和测量报告等功能。因此,在仿真模型中可以假定MS的移动速度极慢或者静止,假定周围环境不会有大的变化,故不同时刻的测量值之间有着较强的相关性。
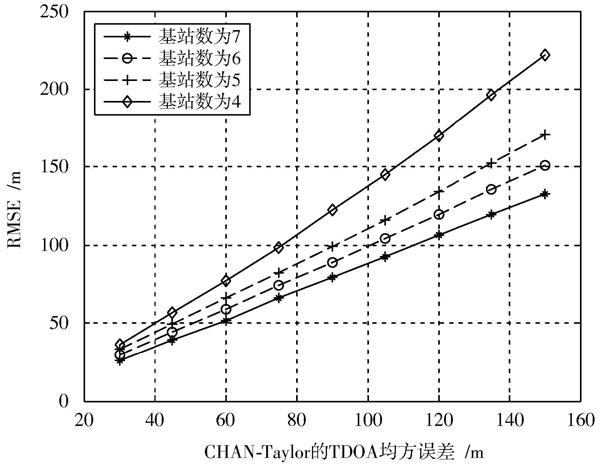
CHAN?Taylor算法在不同基站数下的算法性能如图2所示。在实际应用中,这种算法不对NLOS和LOS进行鉴别,并假设每个测量基站全都有NLOS误差,因此这种算法相当于浪费所有的LOS测量数据。
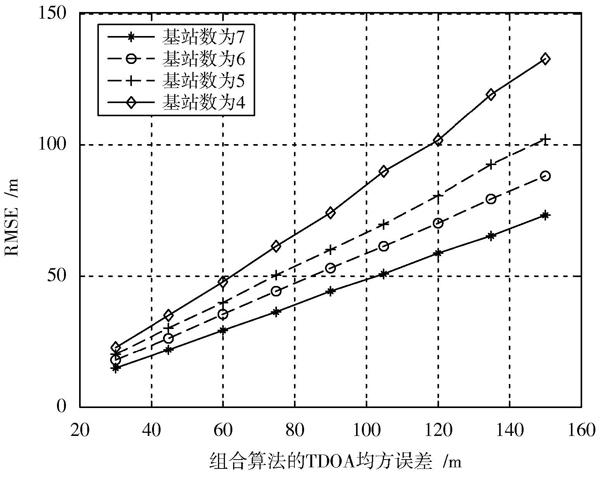
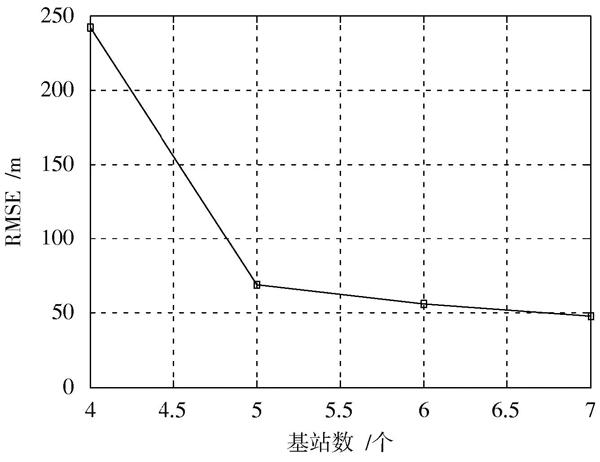
如图3所示是本文组合算法的性能,图4是理想情况不同基站下克拉美罗下界(CRLB)。仿真中的基站数是指NLOS基站数,LOS基站采用极端条件下最少的4基站假设,在相同参数设置下,本文组合算法的定位性能明显优于不进行NLOS鉴别的协同算法,仿真得到的误差大小也更接近克拉美罗下界(CRLB)。这也证明了在CHAN或Taylor估计量理想的情况下,其相关残差结果在理论上总是小于其对应值。从图4中可以看出,当有4组LOS和5组NLOS测量数据时,算法的性能就已经可以达到精度需求:运营商要求为67%的NB?IoT UE提供50 m水平精度的解决方案[12]。
图2 CHAN?Taylor算法的性能

图3 组合算法的性能
對于NB?IoT最高可达164 dB的覆盖能力来说,在实际使用中获取9组TDOA测量值是很容易的,同时本算法在实际环境中如果能得到更多组数据,也能有效提高本算法的定位精度。
图4 RMSE与基站数目的关系
5 结 语
当信号在非视距环境中传播时,同时存在LOS和NLOS测量值,因此本文采用最小二乘法的改进方法来鉴别非视距误差,然后针对两种不同误差进行组合定位。根据仿真结果,与其他方法相比,这种方法具有更好的定位精度。本文算法虽然有较好的定位效果,但也有一定的缺点。如需要多次测量来减少NLOS误差的影响,就牺牲了一定的保密安全性并加大了系统开销;与传统协同算法相比复杂度有所增加,因此系统时延较大,无法应用于移动态的终端。相信通过对组合定位算法的不断改进,它可以适应更多更复杂的环境,相信在未来5G的大规模物联网通信中有更好的应用前景。
注:本文通讯作者为符杰林。
参考文献
[1] WANG Y, SUN X, HU N, et al. A mobile localization strategy for wireless sensor network in NLOS conditions [J]. China communications, 2016, 13(10): 69?78.
[2] YAN L, LU Y, ZHANG Y. An improved NLOS identification and mitigation approach for target tracking in wireless sensor networks [J]. IEEE access, 2017, 5: 2798?2807.
[3] WANG Y, CHENG L, HU N. Bayes sequential test based NLOS localization method for wireless sensor network [C]// 2015 Chinese Control and Decision Conference. Qingdao, China: IEEE, 2015: 5230?5234.
[4] GAO S, ZHANG F, WANG G. NLOS error mitigation for TOA?based source localization with unknown transmission time [J]. IEEE sensors journal, 2017, 17(12): 3605?3606.
[5] ZHENG Fei, ZHENG Jiyu. Application research of TDOA based CHAN algorithm under the circumstances of LOS and NLOS in UWB system [J]. Application of electronic technique, 2007, 33(11): 110?113.
[6] LU Yin, WANG Baoquan, QIU Jinwei. Study on localization of CHAN Algorithm in LOS and NLOS environment [J]. Computer technology and development, 2015(9): 61?65.
[7] CHENG Long, QI Qianyue, WU Xuehan, et al. A NLOS selection based localization method for wireless sensor network [C]// 2017 International Conference on Electronics Information and Emergency Communication. [S.l.]: IEEE, 2017: 340?343.
[8] HE Y, LI H. A non?line?of?sight error mitigation method in wireless location system [C]// 2009 IEEE International Confe?rence on Computer Science and Information Technology. Beijing: IEEE, 2009: 282?286.
[9] LIN X, BERGMAN J, GUNNARSSON F, et al. Positioning for the Internet of Things: a 3GPP perspective [J]. IEEE communications magazine, 2017, 55(12): 179?185.
[10] DENG P, LIU L, FAN P. A collaborative location model for mobile position estimation [C]// 2003 International Conference on Parallel and Distributed Computing, Applications and Technologies. Chengdu, China: IEEE, 2003: 364?366.
[11] GU Qunying, LI Wenyuan, HE Huan. Time?based cellular system wireless location technology [J]. Modern electronics technique, 2007, 30(7): 31?34.
[12] Ericsson. R1?168553, New simulator for positioning of NB?IoT, RAN1#86 [R]. Japan: Ericsson, 2016.
