LDPC码基于双修正因子的剩余度置信传播译码算法
2019-06-19周华赵良李诚谦
周华 赵良 李诚谦
摘 要: 通过对LDPC码的RBP和NWRBP译码算法进行研究,针对算法在译码过程中运算量过大,不利于在硬件上实现的问题,提出一种改进型的RBP和NWRBP译码算法。该算法在更新从检验节点到变量节点的信息时,采用最小和算法得出近似值,以此降低译码复杂度。同时,为了弥补近似值所带来的译码性能损失,引入乘性修正因子和加性修正因子来提高译码性能。
关键词: LDPC码; RBP算法; NWRBP算法; 最小和算法; 修正因子引入; 信息更新
中图分类号: TN919.3+2?34 文献标识码: A 文章编号: 1004?373X(2019)11?0015?04
Abstract: The residual belief?propagation (RBP) and node?wise residual belief?propagation (NWRBP) decoding algorithm for low?density parity?check (LDPC) codes is researched, but it has excessive computing amount in decoding process, and is difficult to implement with hardware. Therefore, the improved RBP and NWRBP decoding algorithm are proposed. When the algorithm is used to update the information from check nodes to variable nodes, the Min?Sum (MS) algorithm is adopted to obtain the approximate value, so as to reduce the complexity of decoding. In the meanwhile, in order to compensate for the decoding performance loss caused by the approximate value, the multiplicative correction factor and additive correction factor are introduced to improve the decoding performance successfully.
Keywords: low?density parity?check code; residual belief?propagation algorithm; node?wise residual belief?propagation algorithm; Min?Sum algorithm; correction factor introduction; information updating
0 引 言
低密度奇偶校验码(Low?Density Parity?Check Codes,LDPC)[1]是一种由二进制稀疏矩阵定义的线性分组码。由于较强的纠错能力和较大的灵活性,以及在加性高斯白噪声下其置信传播(BP)译码算法的性能逼近香农限,LDPC成为近些年来编码领域研究的热点,并且LDPC码于北京时间2016年10月14日被确定为5G 长码编码方案。
在众多的LDPC译码算法中,剩余度置信传播(Residual Belief?Propagation,RBP)和基于行的剩余度置信传播(Node?wise RBP,NWRBP)算法[2?3]是一种高效的动态调度译码算法[4]。
RBP和NWRBP作为有效的动态调度译码算法,它们具有良好的译码性能,特别是在迭代次数较低的情况下这种优势更加明显。然而,RBP和NWRBP算法在译码过程中需要大量地使用指数型和对数型乘法运算,特别是在译码时需要多次使用tanh函數,计算相当复杂,在实际应用中需要通过查表才能实现,因此需要占用大量的ROM资源,不利于硬件的实现[5?8]。
改进型RBP和NWRBP算法采用加法运算替代计算剩余度值过程中的指数型和对数型乘法运算,以便降低译码的复杂度,但也同时带来了误码率的提高。为了弥补降低运算复杂度而带来的译码性能上的损失,本文引入双修正因子[α]和[β]对剩余度值的计算进行修正[9],从而改善译码性能。
1 LDPC码的RBP和NWRBP译码算法
假设一个[(N,M)]的LDPC码,检验位数量为[M=N-K],则检验矩阵[H]是一个[M×N]的矩阵。[H]矩阵中的[M]行和[N]列分别对应Tanner图中的[M]个校验节点和[N]个变量节点[10],其中,校验节点集为[cii=1,2,…,M],变量节点集为[vjj=1,2,…,N]。在信息的传输过程中,使用二进制移相键控(Binary Phase Shift Keying,BPSK)将二进制码字序列[z=(z1,z2,…,zN)]调制成[x=(x1,x2,…,xN)]传送出去,经加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道后接收到的序列[y=(y1,y2,…,yN)]为:
式中:BPSK的调制映射规则为[xi=2zi-1, i=1,2,…,N];[ni]是服从均值为0、方差为[σ2]的高斯白噪声,即[ni~N0,σ2],且它们之间相互独立。信噪比(Signal?to?Noise Ratio,SNR)记为[EbN0],[Eb]和[N0]分别用于表示每个信息比特发送之前的能量和噪声功率谱密度[2][N0=][2σ2]。在译码前,接收序列的对数似然比(LLR)初始化为:
定义如下记号:[Nci=vjhij=1]表示Tanner图中所有与第[i]个校验节点连接的一组变量节点的集合;[Nci\vj]表示[Nci]除去第[j]个变量节点后得到的子集;[Nvj=cihij=1]表示Tanner图中所有与第[j]个变量节点连接的一组校验节点的集合;[Nvj\ci]表示[Nvj]除去第[i]个校验节点后得到的子集;[Mvj→ci]表示从第[j]个变量节点向第[i]个校验节点发送的信息;[Eci→vj]表示第[i]个校验节点向第[j]个变量节点发送的信息。且有以下定义:
式(3)和式(4)具体描述了LDPC算法在译码过程中任意两个变量节点和校验节点之间消息更新及传递的信息方程[2]。RBP和NWRBP算法是Informal Dynamic Scheduling(IDS)策略中两个基于剩余度值的主要算法机制。剩余度值用于表示从校验节点到变量节点信息更新前后值之差的绝对值。在LDPC解码中,剩余度值用公式表示为:
式中:[Enewci→vj]和[Eci→vj]分别表示从校验节点[ci]向变量节点[vj]发送的更新之前和之后的消息。
RBP和NWRBP的译码计算步骤见算法1。
算法1:RBP和NWRBP算法译码流程
1) 初始化:所有[Eci→vj]设置为0;将所有的[Mvj→ci]值设置为[ri]。
2) 根据式(5)计算所有的剩余度值[R(Eci→vj)]。
3) 找出最大的剩余度值[R(Ecmax→vmax)]。
4) 将所有的剩余度值[R(Eci→vj)]设置为0。
5) RBP后续更新:
2 改进型的RBP和NWRBP译码算法
RBP和NWRBP算法的译码过程中,在计算[Eci→vj]时需要多次使用tanh函数,其计算的复杂度远高于BP算法,根据它们所设计出的译码电路相当复杂,难以推广使用。在使用RBP或NWRBP算法进行译码时的计算过程与BP算法中计算从校验节点[ci]到变量节点[vj]的消息方法一致,而BP算法在计算这一消息值时可通过最小和(Min?Sum,MS)的方式降低运算量。因此,在RBP和NWRBP算法中引入MS来代替式(4),其具体的计算过程为:
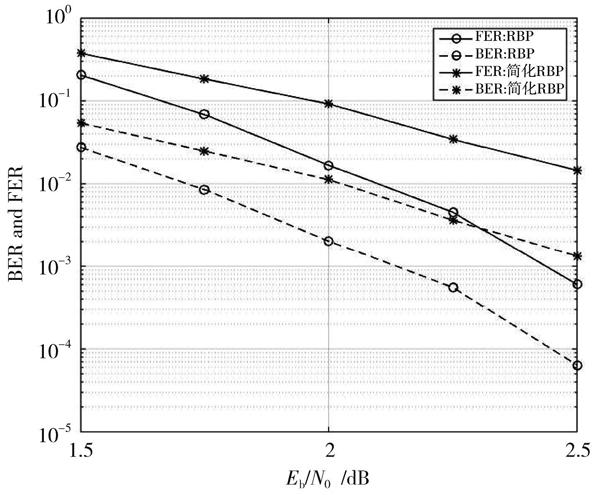
采用MS方式能够用加法运算代替计算[Eci→vj]过程中的浮点型指数和对数乘法运算。由于MS算法是通过近似计算而得出的结果,该方法应用在RBP和NWRBP算法中必然会导致其译码性能的下降。对于码长为155,码率为[12]的规则LDPC码,对RBP进行简化运算,化简后RBP的误码率和误帧率如图1所示。
图1 简化后RBP的误码率和误帧率对比

根据tanh函数的性质可知,通过式(6)计算出的[Eci→vj]要比通过式(4)计算出的[Eci→vj]值略大,这造成了译码性能的损失。为了使通过近似方式计算出的[Eci→vj]值更加接近标准值,引入乘性修正因子[α]和加性修正因子[β]对[Eci→vj]进行修正来提高译码算法的性能,且[α]和[β]满足关系[0<β<α]<1。将[Eci→vj]修正之前和之后分别标记为[E(1)ci→vj]和[E(2)ci→vj],则有:
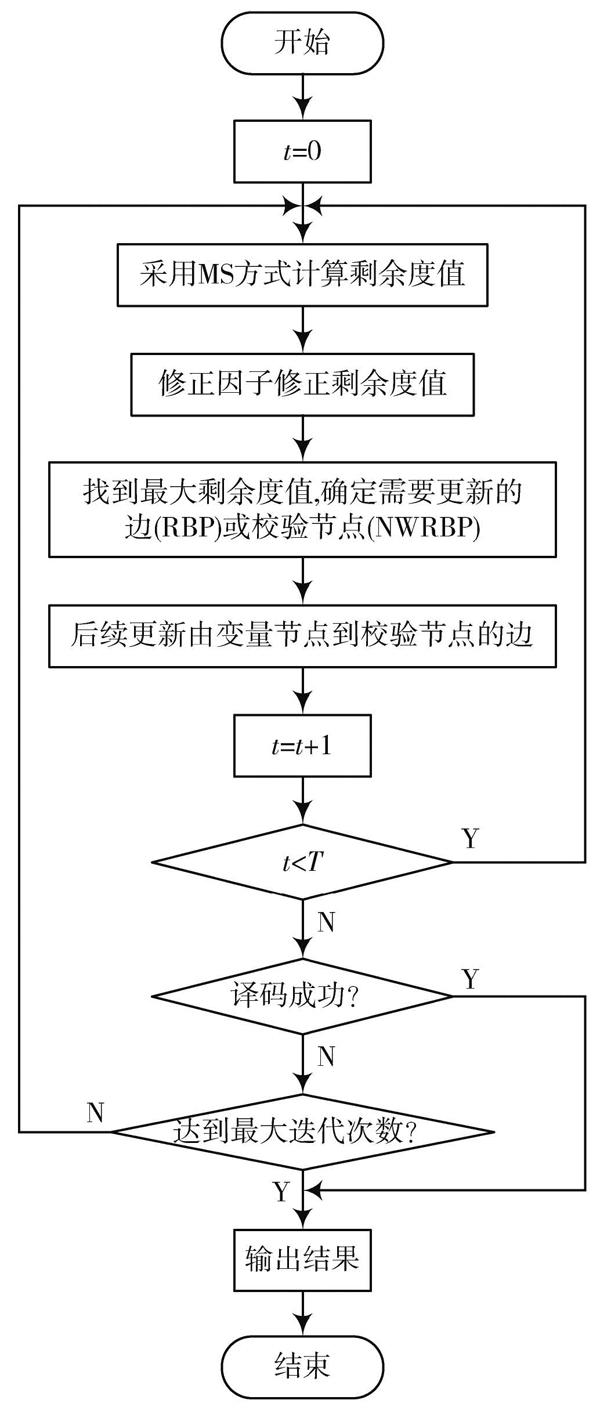
该修正方法根据[E(1)ci→vj]值的大小进行有差别的修正,即[E(1)ci→vj]的修正幅度随着[E(1)ci→vj]值的增大而增大。如果想要获得更好的译码性能,修正因子需要根据信道条件和传输码长的变化而变化,但一般可以作为常数进行处理,这里将修正因子[α]和[β]分别取0.9和0.1,具体的计算步骤见算法2,算法流程如图2所示。
算法2:改进型RBP和NWRBP算法译码流程
1) 初始化:将所有[Eci→vj]设置为0;所有的[Mvj→ci]值设置为[ri]。
2) 根据式(6)计算[Enewci→vj]的估值,并通过式(7)对[Enewci→vj]值进行修正。
3) 根据式(5)計算所有的剩余度值[R(Eci→vj)]。
4) 找出最大的剩余度值[R(Ecmax→vmax)]。
5) 将所有的剩余度值[R(Eci→vj)]设置为0。
6) RBP后续更新:
7) 尝试判决:
IF未正确译码或没有达到最大迭代次数
图2 基于双修正因子的RBP和NWRBP的译码流程图

根据以上分析,改进型的RBP和NWRBP译码算法相对于原算法做出了两点改进。首先通过加法运算替代乘法运算得出[Eci→vj]的近似值,从而避免tanh函数的计算,以便对硬件电路进行简化;然后,为了弥补近似计算带来的译码性能的损失,引入双修正因子[α]和[β]对[Eci→vj]进行修正,从而达到降低计算复杂度的同时进一步提升译码性能的目的。
3 仿真结果与分析
为了进一步验证该改进型的RBP和NWRBP算法的译码性能,选用Visual Studio 2012软件作为平台,并采用C++语言进行仿真实验。本文所有的实验数据均是在加性高斯白噪声(BI?AWGN)信道下仿真获得的,并通过BPSK方式进行调制。仿真选用IEEE 802.16e标准中码长为155,码率[R=12]以及IEEE 802.16e标准中码长为576,码率[R=12]的规则LDPC码。具体的仿真结果如图3~图5所示。
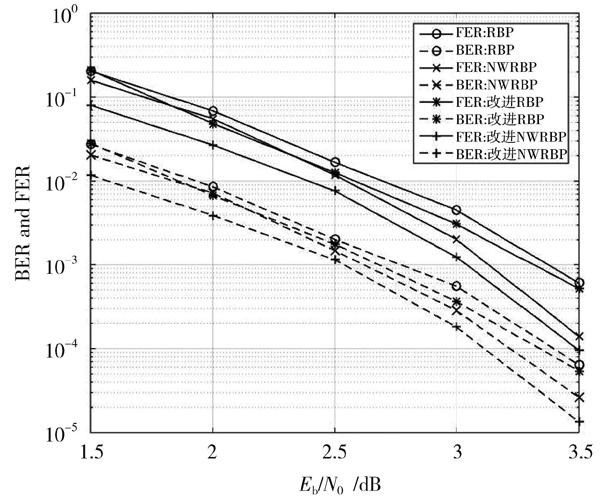
图3 码长为155时改进型的RBP和NWRBP算法的译码性能

图4 码长为576时改进型RBP算法的译码性能
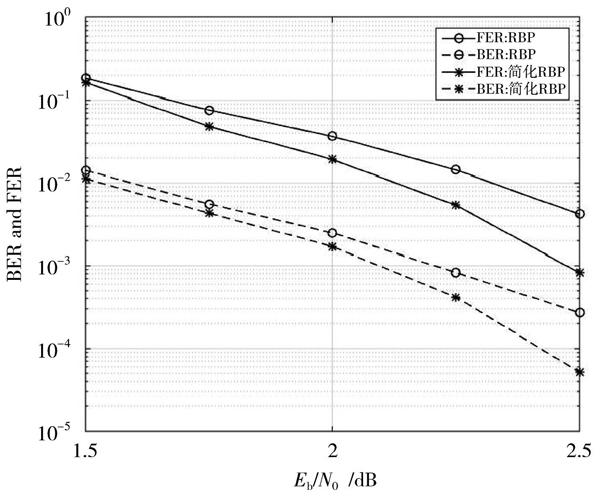
图5 码长为576时改进型NWRBP算法的译码性能
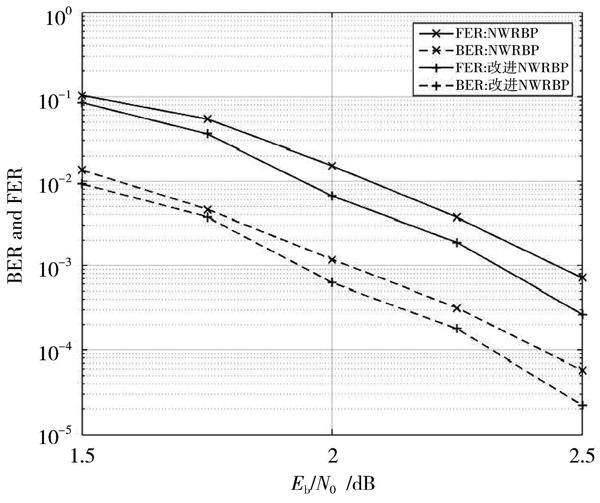
图3和图4分别为码长155,码长576,[α]和[β]分别取0.9和0.1,最大迭代次数为50的情况下各种译码方案的性能对比。在信噪比较低时,改进型RBP和改进型NWRBP与传统的RBP和NWRBP相比,其误码率和误帧率曲线相差不大。在较高的信噪比情况下,改进型的RBP和NWRBP算法的误码率和误帧率曲线均明显低于传统的RBP和NWRBP算法。码长为155时,如图3所示,改进型的RBP和改进型的NWRBP在误帧率FER为[10-2]的情况下其SNR分别得到0.2 dB和0.15 dB的增益;码长为576时,如图4和图5所示,改进型的RBP和改进型的NWRBP在误码率BER为[10-3]的情况下其SNR分别得到0.15 dB和0.13 dB的增益。
4 结 论
本文针对RBP和NWRBP算法在译码过程中计算复杂度高的问题做出改进,得到一种改进型的RBP和NWRBP译码算法。该算法通过在计算剩余度值[R(Ecmax→vmax)]时采用加法运算代替乘法运算的MS方法,从而使运算的复杂度得到明显下降。为保证译码性能,本文又引入乘性修正因子[α]和加性修正因子[β]进行修正。仿真结果表明,改进型的RBP和NWRBP在155和576两种码长下均具有良好的译码性能,且误码率低于传统的RBP和NWRBP算法。
参考文献
[1] 吴军,廖鑫,张小红.一种改进的LDPC码低復杂度最小和算法[J].电视技术,2015,39(1):88?91.
WU Jun, LIAO Xin, ZHANG Xiaohong. Improved Min?Sum algorithm with low complexity for decoding LDPC codes [J]. Vi?deo engineering, 2015, 39(1): 88?91.
[2] 周华,翁少辉,冯姣. LDPC码节点剩余度置信传播译码改进[J].电子技术应用,2017,43(11):107?111.
ZHOU Hua, WENG Shaohui, FENG Jiao. Enhanced node?wise residual belief propagation for LDPC codes [J]. Application of electronic technique, 2017, 43(11): 107?111.
[3] 张福星,许生旺.一种改进的多元LDPC码译码算法[J].无线电通信技术,2016(6):56?58.
ZHANG Fuxing, XU Shengwang. Modified?BP decoding algorithm of non?binary LDPC codes [J]. Radio communications technology, 2016(6): 56?58.
[4] GONG Y, LIU X C. Effective informed dynamic scheduling for belief propagation decoding of LDPC codes [J]. IEEE transactions on communications, 2011, 59(10): 2683?2691.
[5] LIU Xingcheng, ZHANG Yuanbin, CUI Ru. Variable?node?based dynamic scheduling strategy for belief?propagation deco?ding of LDPC codes [J]. IEEE communications letters, 2015, 19(2): 147?150.
[6] SONG Lingyan, HOU Shujuan. Improved decoding of LDPC codes by variable?to?check residual belief propagation [C]// 2015 International Conference on Communications & Networ?king in China. Shanghai, China: IEEE, 2015: 163?166.
[7] 韩少聪,高飞飞,李云洲.一种改进的自纠正最小和LDPC码的译码算法[J].电信科学,2013,29(6):89?93.
HAN Shaocong, GAO Feifei, LI Yunzhou. An improved self?correct Min?Sum decoding algorithm for low?density parity?check code [J]. Telecommumications science, 2013, 29(6): 89?93.
[8] ELIDAN G, MCGRAW I, KOLLER D. Residual belief propagation: informed scheduling for asynchronous message passing [C]// Proceedings of the 22nd Conference on UAI. Cambridge, MA: MIT Press, 2006: 165?173.
[9] CASADO A, GRIOT M, WESEL R D. Informed dynamic scheduling for belief?propagation decoding of LDPC codes [C]// Proceedings of 2007 ICC. Glasgow, Scotland: IEEE, 2007: 932?937.
[10] LI Hua, ZHENG Linhua. Efficient puncturing scheme for irregular LDPC codes based on serial schedules [J]. IEEE communications letters, 2015, 19(9): 1508?1511.
