基于Otsu算法与直方图分析的自适应Canny算法的改进

梁肇峻 钟俊

摘  要： Canny算子在边缘检测领域被广泛应用，但传统的Canny算子需要人为设定梯度阈值和合适的高斯标准差，因此自动化程度不高。为解决Canny算子的自适应性，发展了包括Otsu算法在内的自适应算法。但传统的Otsu算法存在定位精度不高，易受高斯滤波标准差影响等问题。在Otsu算法的基础上，通过对高斯滤波后梯度图像的分析与研究，对最大类间方差进行改进，从而提高自适应算法的稳定性。将改进后的类间方差与类内方差的比值作为阈值选取的评价标准，从而有效提高了自适应算法的定位精度。仿真表明，所提出的改进算法能有效提高Canny算法的定位精度和鲁棒性。

关键词： 边缘检测; 算法改进; Canny算法; Otsu算法; 自适应算法; 定位精度

中图分类号： TN911.73?34                        文献标识码： A                       文章编号： 1004?373X（2019）11?0054?05

Abstract： Canny operator is widely used in the field of edge detection， but it has low automation degree because the man?made setting of gradient threshold and suitable Gauss standard deviation. In order to improve the adaptivity of Canny operator， the adaptive algorithm including Otsu algorithm was developed. Unfortunately， the traditional Otsu algorithm has low positional accuracy， and is easy to be influenced by Gauss standard deviation. On the basis of studying the Otsu algorithm， the gradient image after Gaussian filtering is analyzed and researched， and the maximum interclass variance is improved to enhance the stability of adaptive algorithm. The ratio of the improved interclass variance and intraclass variance is taken as the evaluation criterion of threshold selection to improve the positional accuracy of adaptive algorithm. The simulation results show that the improved algorithm proposed in this paper can improve the positioning accuracy and robustness of Canny algorithm effectively.

Keywords： edge detection; algorithm improvement; Canny algorithm; Otsu algorithm; adaptive algorithm; positional accuracy

0  引  言

边缘保存了图像的大量重要信息，且边缘检测也是数字图像处理、图像分析、识别领域的重要课题。传统的边缘检测算子如Roberts，Sobel，prewitt，Kirsch和Laplacian等都是局域窗口梯度算子，由于它们对噪声敏感，所以在处理实际图像中效果并不理想。Canny J F提出了边缘性能评估的三准则，并在其基础上设计了Canny算子。

Canny算子是一种基于最优准则推导出来的边缘检测算法，具有定位精度高、检测准确等优点。虽然近年来研究人员在边缘检测中引入小波变换[1]、数学形态学[2]、蚁群算法[3]等新技术，但Canny算子因操作简单、检测性能优越，仍然是目前最优秀的边缘检测技术之一。虽然Canny算子具有以上优势，但是自动化程度不高，受高斯标准差影响大的缺点制约了Canny算子的发展。为了提高Canny算子的自动化水准，文献[4?7]给出了自适应边缘检测的可行性分析及评价标准。文献[8?10]将Otsu算法运用到边缘检测中，文献[11]将类内方差引入到边缘检测中，使Canny具有自适应性。文献[12?13]在图像分割领域对基于灰度的Otsu算法进行改进。

本文结合Canny算子的实际情况，基于对图像梯度直方图的分析，提出针对自适应Canny算子分割效果不理想等问题的改进。对基于Canny算子的经典Otsu算法进行优化，达到提高定位精度和减少因平滑滤波带来的对梯度图像影响的目的。

1  Canny邊缘检测算子的基本原理

两个灰度值不同的区域之间的界限即为边缘，即边缘为图像灰度值不连续的结果。图像的边缘包含了图像的大部分信息，这些信息出现在图像中灰度剧烈变化的地方。

在自适应阈值分割中，Otsu算法一直被认为是最优秀的方法之一，其目标是选取出能使目标与背景的分离性最好，类间差别最大的分割阈值。而与之对应的类内方差则是选取出能使类内差别最小的阈值作为最优分割阈值。

2  基于Canny的自适应算法

2.1  不同自适应算法的比较

图像可以分为目标和背景两部分。方差是图像中像素灰度分布均匀性的一个评价指标，若组成图像的目标与背景两部分的差别越小，则方差值越小。若背景和目标被错误的划分时，会导致两部分的方差变小，因此，错分概率最小是类间方差分割阈值的基本思想[13]。而类内方差反映的是每类像素之间差别的大小，如果边缘集中分布的梯度区间比较狭窄，则分类后的类间方差变化不大。

2.2  类内方差

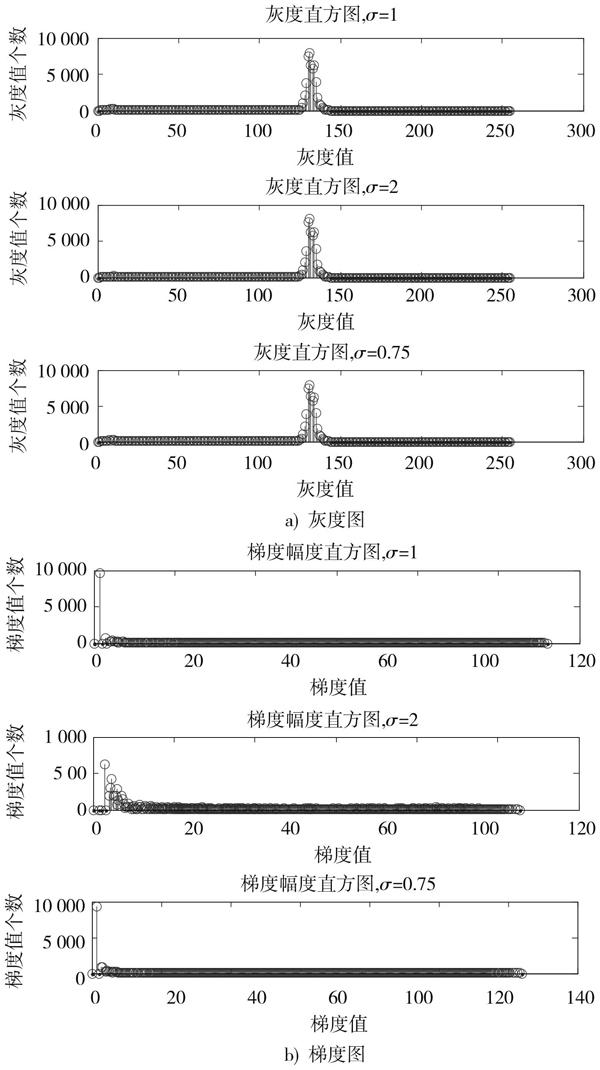
阈值[t]将像素划分为两类：前景[C0] 和背景[C1]。若像素的梯度值[ix，y

2.3  类间方差

类间方差中的[C0]和[C1]分别表示前景与背景部分，其均值[u0]和[u1]与类内方差推导方式相同。

3  基于直方图的Canny自适应算法的改进

3.1  经典自适应算法的改进应用

由于类间方差和类内方差是基于图像的不同性质，所以针对直方图不同的图片，它们会产生不同的效果。因此，最理想的阈值分割是类间方差最大同时类内方差最小。而在实际运用中，不可能完全满足这两个条件，但是能找到兼顾两类方差的最佳分割值，即兼顾考虑以上两类方差并使之得出最优解。为了达到这一目标，将类间方差与类内方差的比值作为分割标准，当比值最大时梯度值作为阈值分割的结果。现定义如下：

3.2  对类间方差的改进

由于经典的Canny算子使用高斯滤波抑制噪声，滤波效果取决于高斯标准差[σ]。当[σ]取值不同，会对图像的直方图产生影响。[σ]较大，会在有效抑制噪声的同时牺牲边缘特性;[σ]过小，会在边缘检测的结果中产生虚假边缘。[σ]对直方图梯度值和权值的影响导致其对传统自适应Canny算法的效果差别很大。

梯度均值反映的是非极大值抑制后梯度的区域平均值;梯度平均方差反映了图像梯度分布的均匀性，即离散程度[5]。[σ]变化，由于图像的边缘特性变化，图像的梯度均值也会相应变化，因而梯度均值受[σ]影响较大。受[σ]的影响，梯度图线性变化，内部性质不变;而平均方差反映的离散程度是梯度内部的性质，所以平均方差受[σ]的影响小。

因此，在[σ]取值不同的情况下，文献[14]中用均值求阈值的方法稳定性较差。其次，当图像的梯度分布较为集中时，梯度区间通常比较狭窄，均值求取的类间方差并不能准确反映目标与背景梯度的区别;而使用平均方差表示的类间方差却依然能表示区域的离散程度。为了达到上述效果，将类间方差改进为：

选取比值最大时的梯度值[h2]作为自适应阈值分割的高门限值，低门限[h1]=0.4[h2]。由Canny算子的基本原理知：[h1]越小，越有利于保留边缘信息，边缘连续性越强;随着[h1]的增加，检测到的边缘特征越来越少，甚至会出现边缘断裂[8]。

4  算法性能分析

4.1  边缘定位特性

选取先验知识为G，记算子检测的边缘结果图像为F。分别对F和G进行扫描，标记它们中相同的边缘像素。则错检点为F中未标记的边缘像素，漏检点为G中未标记的边缘像素[5]。定义错检率和漏检率为：

4.2  梯度均值与方差的比较

如前所述，梯度均值受高斯标准差[σ]影响大而梯度平均方差受其影响小。选取它们各自与先验知识的G偏移的百分比的平均方差作为评价它们受[σ]影响程度的标准。定义如下：

5  实验结果及分析

选取一幅大小为220×256未处理过的图1进行实验，实验工具为Matlab 2012b。

5.1  不同[σ]情况下直方图分析

图2为实验图像在不同标准差情况下的灰度图和梯度图的对比。

由以上实验可知，当[σ]取值不同，直方图会出现不同变化，经过不同标准差滤波后的梯度直方图在梯度值和梯度值权重上面均有明显变化。实验还说明了高斯标准差[σ]对梯度值有较大影响，若使用平均梯度作为自适应计算的标准，计算结果将受到[σ]的严重影响。而梯度直方图的变化是导致自适应Canny算法效果不同的原因所在。

图2  当[σ]取不同值时的灰度图和梯度图

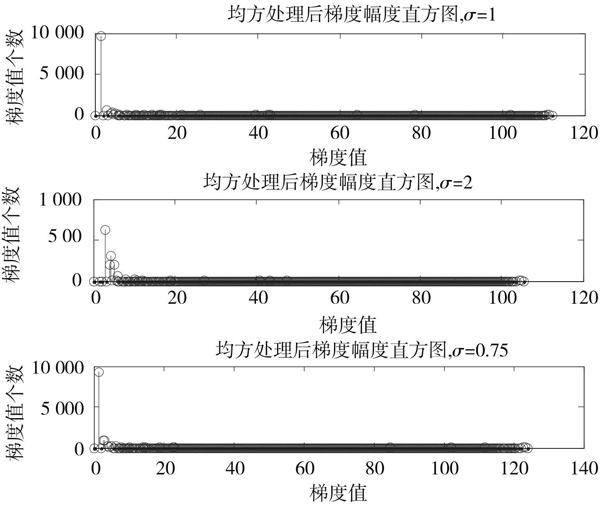
5.2  改进后算法的直方图分析

实验图像经过不同方差处理后的梯度图如图3所示。

图3  平均方差处理后当[σ]取不同值时的梯度图

由圖3可以看出，改进后的梯度图受不同高斯标准差影响较小，因此，使用本文算法中平均方差代替均值的算法改进可以有效提高算法的稳定性。

5.3  算法性能分析

5.3.1  边缘定位特性

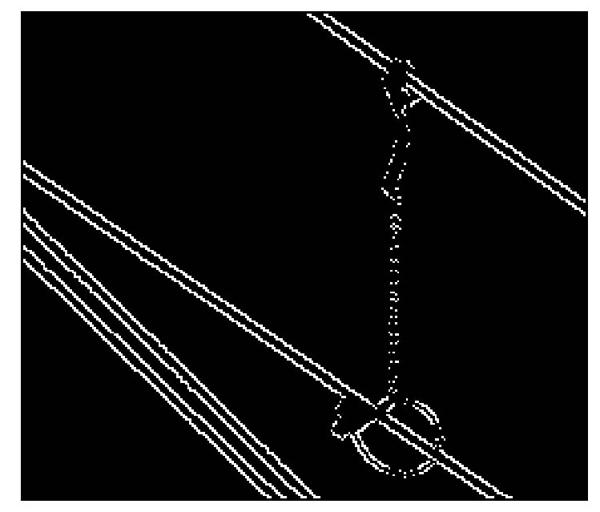
经过反复实验，当梯度值取31.40，高斯标准差取0.65时，边缘检测的效果最佳，记为先验知识[G]，如图4所示。

图4  先验知识

5.3.2  梯度均值与方差的比较

表1为本文选取的实验图片经过本文改进后算法的边缘特性与原算法的边缘定位特性的性能对比。表2为实验图片在不同高斯标准差情况下梯度均值与方差的变化对比。

表1  边缘定位特性

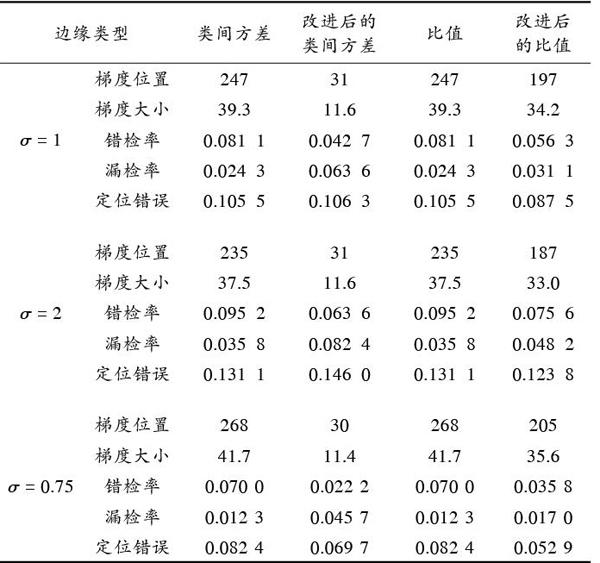
表2   梯度均值与方差

5.3  实验结果分析

基于以上分析，得出以下结论：

1） 相同高斯标准差情况下，改进后的类间方差的错检率低于改进前的结果。

2） 改进后的比值法求出的梯度图像，在连续性上优于改进前的类间方差，在减少伪边缘方面优于改进后的类间方差。

3） 不同高斯标准差对比，改进前的类间方差对高斯标准差较敏感，而高斯标准差对改进后的类间方差影响不大，并且改进后的比值法对不同高斯标准差的稳定性也明显提高。由此可知，经过均方差改进的类间方差提高了梯度图像的鲁棒性。

4） 改进后的比值法定位错误明显低于未改进的结果，定位精度得到明显的提升。

6  结  语

本文针对Otsu算法应用在Canny自适应边缘检测中存在的问题进行改进。首先，通过在算法中使用平均方差的方法，使改进后的边缘检测结果受高斯标准差影响微小。其次，通过改进的Otsu门限分割法能计算出比原算法更准确的门限值。实验结果表明，在Canny边缘检测中应用本文的算法，在保证原算法自动化的基础上提高了边缘检测的定位精度和鲁棒性，得出了更好的结果。

参考文献

[1] 刘芳，邓志仁.基于自适应小波阈值和双边滤波器的去噪算法[J].系统仿真学报，2014，26（12）：2934?2938.

LIU Fang， DENG Zhiren. Denoising algorithm based on adaptive wavelet threshold and bilateral filter [J]. Journal of system simulation， 2014， 26（12）： 2934?2938.

[2] 戴青云，余英林.数学形态学在图像处理中的应用进展[J].控制理论与应用，2001，18（4）：478?482.

DAI Qingyun， YU Yinglin. The advances of mathematical morphology in image processing [J]. Control theory and applications， 2001， 18（4）： 478?482.

[3] 解欢庆.改进的蚁群算法在图像边缘检测中的应用研究[D].兰州：兰州大学，2011.

XIE Huanqing. Application research of improved ant colony algorithm in image edge detection [D]. Lanzhou： Lanzhou University， 2011.

[4] 雒涛，郑喜凤，丁铁夫.改进的自适应阈值Canny边缘检测[J].光电工程，2009，36（11）：106?111.

LUO Tao， ZHENG Xifeng， DING Tiefu. Improved self?adaptive threshold Canny edge detection [J]. Opto?electronic engineering， 2009， 36（11）： 106?111.

[5] 张心言，赵冉阳.基于Canny的自适应边缘检测算法及性能评估[J].计算机技术与发展，2015，25（11）：32?37.

ZHANG Xinyan， ZHAO Ranyang. An adaptive edge?detection algorithm based on Canny and its performance evaluation [J]. Computer technology and development， 2015， 25（11）： 32?37.

[6] 磨少清.边缘检测及其评价方法的研究[D].天津：天津大学，2011.

MO Shaoqing. Study on edge detection and its evaluation method [D]. Tianjin： Tianjin University， 2011.

[7] BAO Paul， ZHANG Lei， WU Xiaolin. Canny edge detection enhancement by scale multiplication [J]. IEEE transactions on pattern analysis and machine intelligence， 2005， 27（9）： 1485?1490.

[8] 梁光明，孙即祥，马琦，等.Otsu算法在Canny算子中的应用[J].国防科技大学学报，2003，25（5）：36?39.

LIANG Guangming， SUN Jixiang， MA Qi， et al. Application of Otsu algorithm in Canny operator [J]. Journal of University of Defense Technology， 2003， 25（5）： 36?39.

[9] 金刚.自适应Canny算法研究及其在图像边缘检测中的应用[D].杭州：浙江大学，2011.

JIN Gang. Research on adaptive Canny algorithm and its application in image edge detection [D]. Hangzhou： Zhejiang University， 2011.

[10] 劉超，周激流，何坤.基于Canny算法的自适应边缘检测方法[J].计算机工程与设计，2010，31（18）：4036?4039.

LIU Chao， ZHOU Jiliu， HE Kun. Adaptive edge?detection method based on Canny algorithm [J]. Computer engineering and design， 2010， 31（18）： 4036?4039.

[11] 傅仲良，李勇.基于梯度幅度直方图和类内方差的边缘提取方法[J].武汉大学学报（信息科学版），2005，30（12）：1056?1058.

FU Zhongliang， LI Yong. Edge detection based on gradient histogram and variance within clusters [J]. Geomatics and Information Science of Wuhan University， 2005， 30（12）： 1056?1058.

[12] 邱丽君.Otus图像分割方法的研究与应用[D].济南：山东师范大学，2011.

QIU Lijun. Study and application of Otus image segmentation method [D]. Jinan： Shandong Normal University， 2011.

[13] 李惠光，姚磊，石磊.改进的Otsu理论在图像阈值选取中的应用[J].计算机仿真，2007，24（4）：216?220.

LI Huiguang， YAO Lei， SHI Lei. Automatic selection of image threshold based on improved Otsu [J]. Computer simulation， 2007， 24（4）： 216?220.

[14] MEER P， GEORGESCU B. Edge detection with embedded confidence [J]. IEEE transactions on pattern analysis and machine intelligence， 2001， 23（12）： 1351?1365.

[15] RACHID D. Using Canny′s criteria to deriver a recursively implemented optimal edge detector [J]. International journal of computer vision， 1987， 1（2）： 167?187.