某共轴双旋翼无人直升机旋翼桨距操纵分配研究

董 鹰，戴梦漪，翟剑豪

(庆安集团有限公司 航空设备研究所，陕西 西安 710077)

0 引言

直升机比固定翼机操纵控制复杂的一个特点就是直升机旋翼既是其升力面,同时又是操纵面,直升机飞行的纵向、横向、航向姿态变化的力、力矩均由旋翼提供[1]。而其改变姿态和航迹所需的操纵作动均由直升机旋翼操纵系统提供。其过程是根据直升机姿态和航迹的需求，直升机飞控系统经过运算协调，向舵机系统发送操纵指令，由舵机系统保证执行机构达到所需的位置，从而改变旋翼总距、周期变距以及总距差动，满足直升机的姿态和航迹。

本文的目的是根据我公司研制的某型共轴双旋翼无人直升机旋翼操纵系统的特点，分析其运动规律，建立旋翼操纵分配的数学模型，并对该模型进行误差分析和结果验证，以便于将建立的模型应用到飞控系统中，用于对直升机需求航姿的舵机操纵量进行解算。

1 研究对象

某共轴双旋翼无人直升机旋翼操纵系统如图1所示。该旋翼操纵系统采用了中置操纵的思想，即操纵旋翼桨距的舵机均处于两层旋翼之间，上、下旋翼各由3个舵机对其进行桨距操纵，6个舵机均通过转接结构安装于中置换向齿轮箱上，中置换向齿轮箱及一对锥齿轮安装于带有中心十字突出的中心轴上，中心轴安装于无人直升机机身，并在下端通过支撑机构固定，上、下旋翼轴均为空心轴套装于中心轴上，并通过轴端的花键分别与锥齿轮和上、下桨毂连接。本共轴旋翼操纵机构已申请国家发明专利并获得授权(ZL 201410275790.4)。此处对其工作原理作简要说明：本无人直升机通过上、下舵机同时向上作动，使得上、下自动倾斜器向上运动，上、下旋翼总距增加，产生垂直运动；通过上、下舵机差动作动，使得上、下旋翼总距一个增加一个减小，产生航向力，引起航向运动；通过上、下舵机作动使得上、下自动倾斜器同时向前、后、左、右倾斜，产生相应的分力，引起前、后、左、右方向运动。

图1 某共轴双旋翼无人直升机旋翼操纵系统

2 建模说明及规定

该型共轴双旋翼无人直升机旋翼操纵系统6个舵机完全相同，均通过摇臂输出转矩，但安装于该无人直升机之后，上、下旋翼的3个舵机布局中心对称，其操纵点分别为处于同一个圆上的等边三角形的3个顶点，在操纵时需区分极性，故需对其进行编号，编号规则见图2(b)和图2(c)。

该型共轴双旋翼无人直升机经过CFD计算分析，获得其悬停时总距角为6°，其发动机功率/扭矩最大可驱动旋翼总距角为12°，旋翼在工作中不存在负总距的情况，故旋翼实际工作角度范围为0°～12°，考虑到运动的裕度，可在计算中将操纵总距角范围调大为0°～16°。在实际工作中，可根据需求通过程序标定和调整总距操纵的实际工作范围。

在共轴双旋翼无人直升机的工作过程中，因悬停总距和悬停总距范围附近的总距角度最为常用，

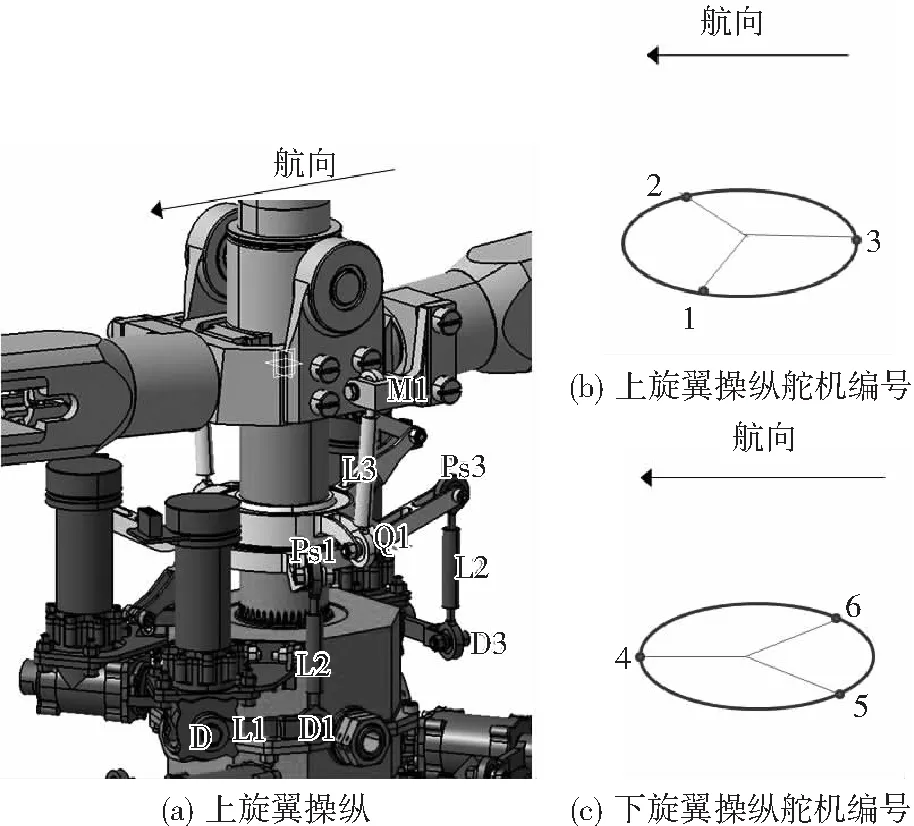
图2 旋翼操纵系统模型及编号规定

故规定悬停总距角为该机的操纵零位(或基准位置)，同时要求在操纵零位附近舵机操纵效率最高，由此推出，零位时上旋翼总距角为6°，舵机摇臂应处于水平方位。

根据图2(a)、图2(b)所示上旋翼操纵系统，做如下规定、设计或假设：

舵机摇臂设为L1，长度设计为60mm；

舵机摇臂与上自动倾斜器静盘连杆设为L2，长度调整为86mm；

上自动倾斜器动盘与桨盘的变距连杆长度设为L3，长度根据零位时舵机摇臂L1水平偏角为0°，上旋翼总距角为6°可计算获得L3=103.4mm；

设静盘与L2连杆连接的3个铰链点分别对应3个舵机，编号规定为Ps1,Ps2,Ps3，该3点处于以旋翼轴心圆心的圆上，其距轴心设计为R1=120mm；

`设L2连杆与舵机摇臂连接的3个铰链点同样对应3个舵机，编号规定为D1，D2，D3，3个舵机摇臂的旋转点编号为D，E，F；

同样，设L3连杆与动盘的铰链点为Q1和Q2，其距旋翼轴心设计为R2=70mm；

设变距连杆L3与旋翼桨毂的铰链点为M1和M2，当旋翼总距为0°时，M1和M2距旋翼轴心设计为R3=80mm；

设变距连杆L3与旋翼轴初始夹角为θ1，变距操纵后为θ2；

设1、2、3号舵机摇臂绕D点旋转，与水平面的偏角分别为β1、β2、β3，且舵机摇臂偏角向上偏为正，向下偏为负；

图3为上自动倾斜器运动示意图：下圆盘表示初始状态时自动倾斜器的位置和姿态，自动倾斜器上静盘的3个铰链点为Ps1、Ps2和Ps3；上圆盘表示3个舵机任意作动后，上自动倾斜器运动后的位置和姿态，自动倾斜器运动后静盘上的3个铰链点为Ps1′、Ps2′和Ps3′。假设3个舵机作动后，自动倾斜器上3个铰链点的位移分别为hs1、hs2和hs3，3个铰链点的圆心位移为hs；

设上旋翼总距角为cs，向上为正，自动倾斜器平面的俯仰角为as，定义前仰为正，自动倾斜器平面的侧滚角为bs，定义左倾斜为正。

3 运动学计算与分析

3.1 总距与自动倾斜器的运动关系

因本共轴双旋翼无人直升机上、下旋翼操纵变距的工作方式相近似，不同之处仅在于上、下旋翼操纵舵机的安装位置中心对称，因此，只需对其中一副旋翼的操纵进行计算，另一幅旋翼的操纵只需做小量变换即可获得结果。故在本文中只对上旋翼操纵进行相关计算与分析，下旋翼可类似得出结果。

总距变化时，自动倾斜器上的4点Ps1、Ps2、Ps3、Ps0同时向上或向下平移，根据图2(a)和图3以及上一节的设定，并对其抽象，可作出图4。

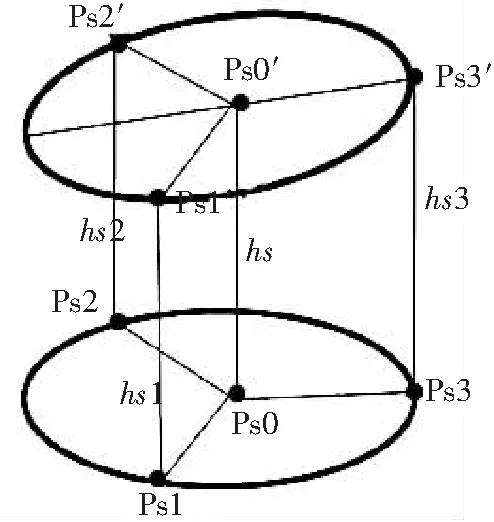
图3 上自动倾斜器运动示意图

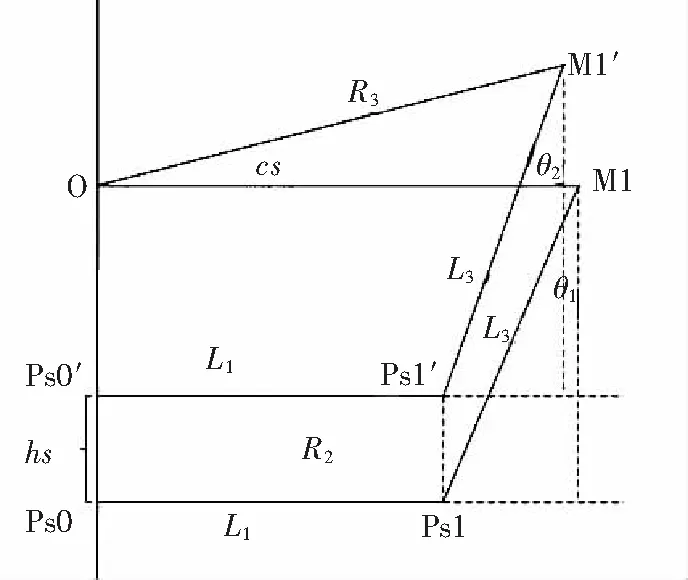
图4 上旋翼总距操纵分析

由图4可获得方程(1)、(2)：

R3-R3×coscs=L3×sinθ1-L3×sinθ2(1)

L3×cosθ2+hs=L3×cosθ1+R3×sincs(2)

根据已知条件R2=70mm，R3=80mm，L3=103.4mm，θ1=5.55°，联合(1)、(2)消除θ2可获得总距角度cs和自动倾斜器位移hs的函数关系(3)：

(3)

利用MATLAB对上式绘制曲线，且取总距角cs范围按前文给出的定义域[0,16],可获得总距角cs与自动倾斜器hs位移的对应数据，如表1所示。

3.2 自动倾斜器位移与舵机摇臂转角的运动关系

总距变化时，舵机摇臂绕D点旋转，根据前文规定，总距为6°时为舵机零位，此时舵机摇臂水平，当总距在0°～6°之间时，舵机摇臂向下运动与水平面夹角βi(i=1～6)为负值，当总距在6°～16°之间时，舵机摇臂向上运动与水平面夹角βi(i=1～6,下同)为正值。根据分析可做舵机摇臂转角与倾斜盘运动简图(如图5)，图中(a)、(b)分别代表舵机摇臂向上和向下运动的情况。

表1 总距角与自动倾斜器位移关系(位移单位：mm)

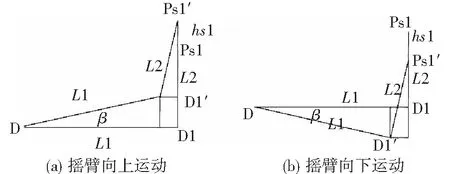
图5 舵机摇臂运动示意图

分析图5中(a)、(b)两种运动情况，下式(4)均成立：

(4)

对于方程(4)，其反函数较难求解，即以hs为自变量求βi较为困难，故利用牛顿迭代法给βi直接赋值获得hs变化范围，并与表1中的hs比较。首先给βi取值-10°～20°，求得hs的范围为-2.1031～28.7657mm(以总距为0°时hs=0为基准)。经过迭代求解最终确定：βi=-7.9694°时，hs为0(此时总距cs=0°);βi=12.9930°时,hs=21.7968(此时总距cs=16°)。故为保证总距cs的运动范围，3个舵机摇臂与水平面夹角βi的定义域为[-7.9694°，12.9930°],该范围处于舵机摇臂零位两侧附近,线性度较好。

3.3 舵机摇臂与总距的运动关系

本文的主要目的是获得舵机与桨距的运动关系，倾斜盘位移是该运动关系的中间过程，故需对前两节获得的关系进行整理，去掉中间变量，获得舵机与总距的直接关系。

为此，需将舵机摇臂倾角βi与旋翼总距cs两者通过自动倾斜器位移hs为桥梁进行关联，但将式(4)直接代入式(3)后，会产生一个高阶非线性超越方程，且因高阶三角函数的关系还可能存在奇异解，故对式(3)中的cs和hs按表1中求得的数据进行多项式拟合[2]，可获得如下关系式(5)：

cs1=0.0004hs2+0.72hs(5)

其中cs1表示拟合值，与真值cs之间存在一定的误差，可将hs=[0，21.7968]代入式(5)，并按式(6)计算其误差，分析是否满足需求。

(6)

利用MATLAB计算的cs1及误差RSS见表2。

表2 总距角与自动倾斜器位移拟合计算及误差分析

分析表2中的误差，可见拟合总距值cs1与真值cs之间的误差最大仅为0.73%左右，且处于最大总距值处，总距绝对误差值仅为0.1162°，与飞行中外界扰动相比属于小量，故cs1可代替cs用于计算。

对上旋翼操纵机构抽象得出图6。图中DD1为舵机摇臂最低位置,Ps0,Ps1为自动倾斜器最低位置,OM1为旋翼摇臂最低位置(总距为0°)。DD1′位舵机摇臂零位,Ps0′,Ps1′和 OM1′分别为自动倾斜器和旋翼摇臂在舵机作用下运动后的位置。

在计算中，式(4)中hs是以总距为0°为基准求解的，此时舵机摇臂向下偏，而式(3)求解时hs是以总距6°时零位为基准的。为保证舵机摇臂偏角和倾斜盘位移在最低位置在定义域上同步，需对式(3)进行6°的补偿，补偿后，舵机摇臂为βi=-7.9694°时，hs=0，对应于总距角0°；βi=0°时，自动倾斜器位移hs=8.3206mm，总距cs=6°。式(3)补偿后获得式(7)：

(7)

将式(7)代入式(5)中可获得舵机摇臂偏转角度对总距的运动关系函数式(8)：

(8)

式(8)中L1和L2均为已知，β定义域已确定，故总距cs值也是随β值唯一确定的。

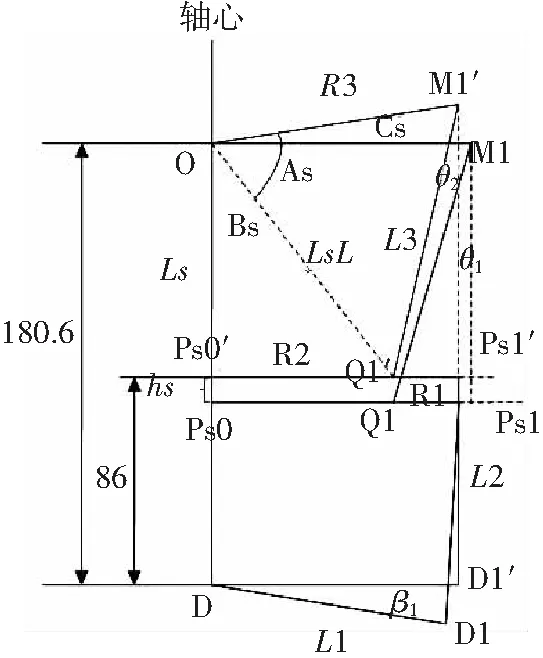
图6 共轴双旋翼无人直升机模型

3.4 舵机摇臂与周期变距的运动关系

在前面三节中对总距与舵机摇臂的运动关系进行了推导，因总距变化是上、下6个舵机同时刻、同方向、同尺度作动的结果，故用一个舵机即可代替其他所有舵机，所获得的运动关系可认为是单变量、单输出关系式，相对简单。而舵机摇臂与周期变距的关系相对复杂，每一层舵机作动时最多是3输入、3输出，还有1输入、3输出，甚至2输入、1输出等情况，具有多种变化规律。在此情况下，简单的关系式无法描述旋翼操纵的所有空间的输入和输出关系，故需用空间转换矩阵来描述舵机摇臂的输入与周期变距、总距变化输出的关系。下面推导该转换矩阵，仍以上旋翼为研究对象，下旋翼做类似推导及简单转换也可获得同样结果。

设舵机零位为初始时刻，此时3个摇臂均处于水平位置，根据前文推导可知，此时自动倾斜器水平，纵向俯仰角a=0°，横向滚转角b=0°，倾斜盘从最低位置向上运动hs=8.3206mm，桨叶总距角cs=6°。如图7，假设此后支撑ps1点的1号舵机摇臂运动了β1，支撑ps2点的2号舵机摇臂运动了β2，支撑ps3点的3号舵机摇臂运动了β3，ps1、ps2、ps3三点的位移分别为hs1、hs2、hs3，自动倾斜器中心点位移为hs0。

图7 周期变距中自动倾斜器运动示意图

此时，自动倾斜器运动分解为沿中心轴方向的平动hs0，对应旋翼总距cs变化，自动倾斜器平面纵向俯仰角变化as，自动倾斜器平面横滚角变化bs，自动倾斜器最高点相对于最低点的差值定义为Δhs。一般来说，as和bs角度均小于10°，所以在此计算中可以忽略运动过程中由于3个舵机运动尺度不同所造成的L2杆向中心轴倾斜角度或者远离中心轴的倾斜角度，仅考虑L2杆在舵机摇臂平面上的左右偏角。

则前文推导的式(4)依旧成立，具有：

(9)

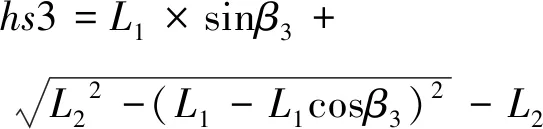
设机体前仰时俯仰角为正，则根据图7，如下关系成立：

(12)

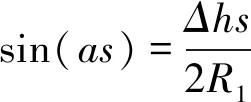
由式(12)和式(13)可得：

(14)

设机体左侧倾时横滚角为正，则根据图7，如下关系式成立：

(15)

P0点的位移与总距具有直接关系，根据前文推导式(5)再考虑补偿角度使总距与舵机摇臂倾角定义域同步，并忽略高阶项，可得如下关系：

cs-6=0.72hs(16)

将式(9)、(10)和(11)分别代入式(14)、(15)和(16)中可得：

sin(as) (17)

sin(bs) (18)

cs-6 (19)

将式(17)、(18)和(19)三式进行整理获得式(20)关系：

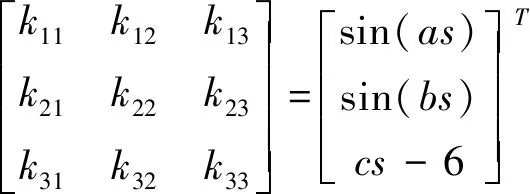
根据图7可知，横滚仅与Ps1和Ps2点的作动有关，Ps3点的作动对横滚不产生贡献，故可知无论何种情况下，下式均成立：

k32=0(21)

又根据自动倾斜器纵横向倾角为0°，即β1=β2=β3时，sin(as)和sin(bs)均为0，可推出：

k11+k21+k31=0(22)

k12+k22=0(23)

再通过对β1、β2、β3分别赋值，并根据前文确定的hs和cs之间的关系以及式(20)求解方程，最终可获得如下关系：

k13+k23+k33=0.72(24)

k11+k21=0.0056(25)

k13+k23=0.48(26)

联立以上6式可获得旋翼操纵空间转换矩阵如下[4]，该矩阵可用来根据任意3个舵机摇臂偏转角求解旋翼总距和周期变距角：

其逆矩阵如下，可用来根据旋翼需求的总距和周期变距求解3个舵机摇臂分别需要的偏转角：

上述矩阵Z即可用于在获得3个舵机偏转角的情况下对旋翼周期变距的求解，同时也包含了对总距的求解，包含了3.3节中推导的总距求解关系式(8)，但也是以式(8)求解为基础的。所以，验证该矩阵以及其逆矩阵是否成立也可用式(8)进行。

经过给出不同的舵机偏角，获得的总距值和周期变距值均与手动逐一求解值吻合，即该转换矩阵及其逆矩阵具有广泛意义，所以可用于飞控系统的程序设计。

4 结论

本文通过对某共轴双旋翼无人直升机上旋翼总距的求解，推导了总距变化与舵机偏转角之间的运动关系，并以此为基础，考虑了舵机偏角对旋翼周期变距的影响。根据已完成的结构设计，获得了上旋翼操纵分配关系及其逆关系。经过取点计算验证，该旋翼操纵分配关系正确。对于下旋翼操纵分配关系及其逆关系，可通过同样的方法推导并验证，本文不再赘述。