轨道不平顺输入数值模拟实验系统设计
2019-06-18李广军毛湘文丁佳慧刘若晨
李广军, 毛湘文, 丁佳慧, 刘若晨
(1. 江苏理工学院 汽车与交通工程学院, 江苏 常州 213001;2. 人工智能四川省重点实验室, 四川 自贡 643000)
随着中国轨道交通的快速发展,高校对轨道车辆工程人才的培养工作和教学方法改革越来越重视[1]。特别是在轨道车辆工程课程体系中,“车辆耦合动力学”是描述轮轨动力学关系的一门重要课程[2],对本专业的人才培养和科技创新起到重要的支撑作用。该课程在讲授过程中,轨道不平顺输入是一个非常复杂和抽象的概念,很难用直观的方法来阐述,但是可以用虚拟仿真实验的方法来辅助其理论教学[3-4]。因此,针对轨道不平顺输入信号,开发了一套轨道不平顺输入数值仿真实验系统。利用该系统,可以方便、快捷地得到所需要的轨道不平顺输入信号,让学生直观、形象地理解轨道不平顺的产生和模拟过程,从而更好地服务于车辆工程本科专业的教学和科研工作。
1 轨道车辆不平顺输入信号产生机理
当列车车轮对轨道表面产生力的作用时,轨道表面也会产生不同程度的损耗,轨头会出现不同程度的损伤。由于轨道的垫面、轨枕、道床和路基具有不同的弹性模量,以及各部件之间具有大小不一的间隙等,将使得轨道的几何形状产生变化,从而出现了不平顺。研究表明:轨道不平顺是一个不确定性过程,它是轨道车辆与轨面产生不确定性振动的重要本源,直接影响轨道车辆的舒适性以及轨道车辆行驶的安全性[5-8]。因此,获得准确的轨道不平顺信号,对于理解和研究铁路车辆动力学具有重要意义。
轨道不平顺可以通过实际线路采集获得,但这种方法需要大量的采集样本,工作量大、成本高[7]。通常的做法是通过对拟合的轨道功率谱进行数值模拟来得到对应的时域样本。这种采集方法因效率高、成本低而被广泛采用。国内外最常用的轨道不平顺时域样本数值模拟主要有三角级数、白噪声滤波、二次滤波和傅里叶逆变换等算法,在车辆耦合动力学系统中已给出各种算法的详细设计过程。针对上述模拟算法设计的轨道不平顺输入信号数值模拟系统可以输入参数和选择算法,从而得到所需要的数值模拟信号,加深对该概念的理解。
2 轨道不平顺数值模拟系统实验系统设计
VC++是具有可视化编译环境的应用软件开发工具,可以开发从底层系统到高层用户的各种应用软件,但是在工程计算和图形显示方面的应用比较烦琐和复杂[9-11];而Matlab虽然具有强大的数据处理、矩阵运算和图形显示功能,但程序解析效率低,不能脱离Matlab环境运行。可以发挥两者的优点,把VC++与Matlab混合起来,编写能独立于Matlab运行环境、且运行效率高的应用程序。这种编程模式并已经被广泛应用到机电产品设计中[12-14]。
VC++与Matlab常用的编程方法有以下几种:(1)VC++调用Matlab引擎法;(2)MATCOM转化法;(3)基于ActiveX控件的方法;(4)使用Matlab Add-in方法;(5)基于COM技术的方法。轨道不平顺数值模拟系统采用了VC++调用Matlab的引擎法,其软件架构和数据流如图1所示。
VC++调用Matlab的应用,Matlab在后台发挥服务器的作用。首先启动VC++6.0,建立环境项目,然后选择Matlab的安装路径,路径配置成功;运行VC++向导,利用Matlab Enginey建立一个对话框应用程序,在主程序***.cpp添加头文件#include ″engine.h″,然后设置联合仿真界面,并调用.m程序。运行仿真结果为.jpg仿真图形,输出为.txt的数据文本文件。

图1 软件框架和数据流图
本实验系统设计流程如图2所示。仿真开始后,首先给出轨道不平顺数值模拟时的列车运行速度、上截止频率和下截止频率。若频率范围输入不正确需重新输入。选择所采用的仿真算法,即从三角级数、白噪声滤波、二次滤波和傅里叶逆变换4种方法中挑选一种,然后调用相应的.m算法文件进行运算。然后,通过Matlab仿真图.fig文件中对比模拟值和解析值,以确定仿真结果是否满足要求:若满足,则仿真结束,并以.txt保存仿真数据(即轨道不平顺数值模拟的位移量);若不满足,则重新进行模拟。开发环境为Windows7操作系统,采用VC++6.0和Matlab R2009a两种软件进行联合仿真。

图2 实验系统流程图
3 数值模拟实例
针对本实验系统,以傅里叶逆变换法模拟美国六级轨道谱作为数值仿真实例,算法原理如下:
(1) 利用轨道不平顺信号双边谱密度函数确定不平顺信号时域序列的频谱幅值。设轨道不平顺信号双边功率谱密度Sx(f),频率采样间隔为Δf,采样周期和总采样时间分别为Δt和ts,则时域序列的频谱幅值为:
(k=0,1,2,…,N-1)
(1)
(2) 为每一个幅值|x(k)|对应一个随机相位ξk。设ξk为复数,|ξk|=1,φk=2πk/N(k=0,1,2,…,N-1),则随机相位ξk表示为
ξk=cosφk+isinφk=eiφk
(2)
(3) 利用傅里叶逆变换,得到轨道不平顺的时域模拟序列x(n)。对由幅值X(k)和相位ξk所构成的频谱序列进行傅里叶逆变换(IFFT),得到轨道不平顺的时域序列模拟样本x(n)。
(n=0,1,2,…,N-1)
(3)
在实验系统界面里,选择了傅里叶逆变换法,然后进入仿真界面。提示选择不平顺种类,然后输入上/下截止频率和列车运行速度等参数。选择方向不平顺之后,设置上/下截止频率分别为300 Hz和50 Hz,列车运行速度为150 km/h,如图3所示。仿真实验界面提示模拟、解析和退出等操作,点击之后得到轨道不平顺模拟值与解析值的功率谱对比,如图4所示。在图4中,点线表示模拟值,实线表示解析值。可以看出:两条曲线几乎重合,误差很小,表明基于数值模拟方法所得到的轨道不平顺信号具有精度高的优点。图5为轨道不平顺数值模拟位移,可以看出:位移的数量级为mm级,符合轨道方向不平顺信号的特征。该信号数据可以.txt文件进行存储,使用时重新打开调出即可。

图3 轨道不平顺数值模拟界面

图4 模拟值与解析值功率谱对比
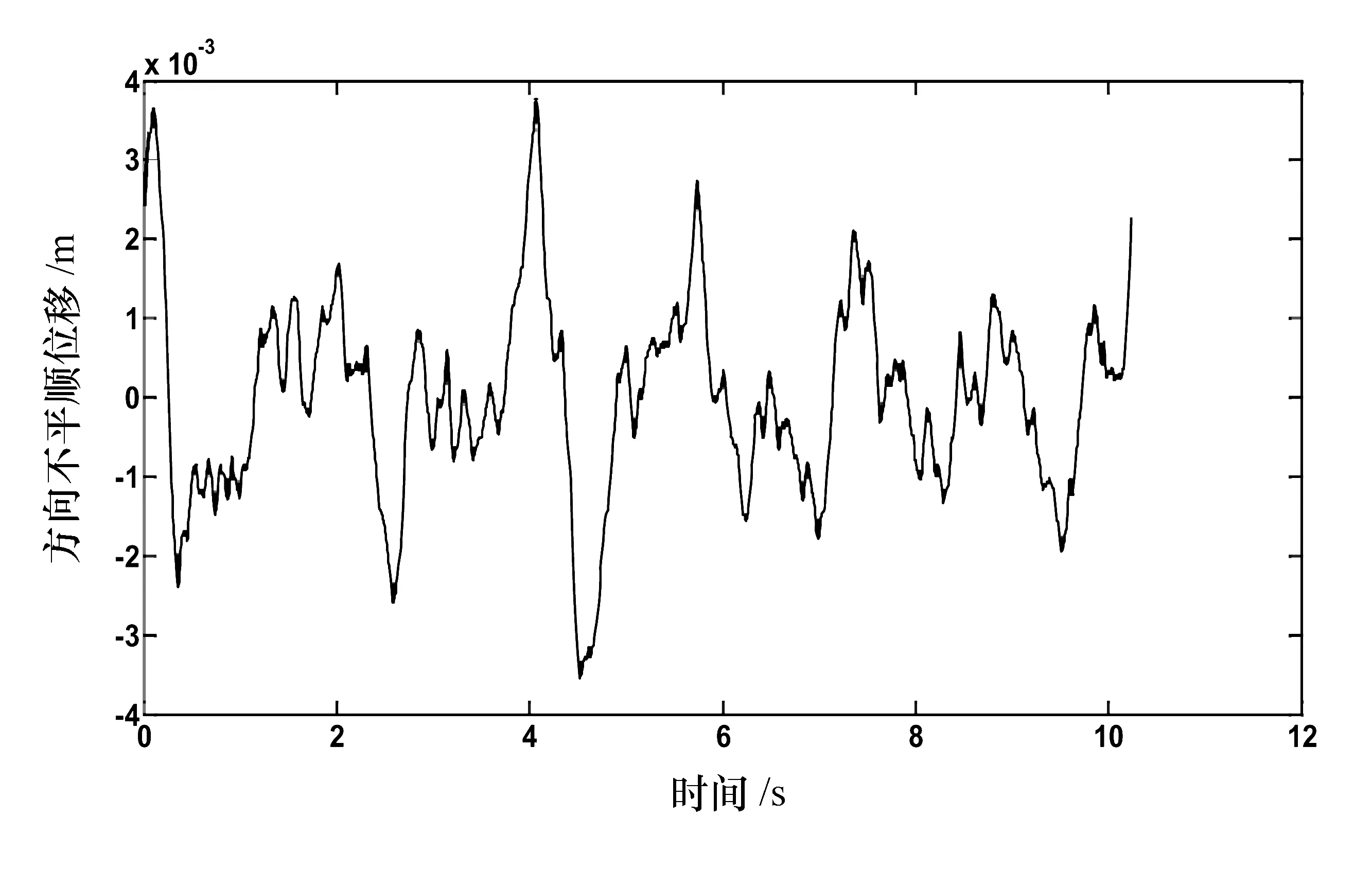
图5 轨道不平顺数值模拟位移
4 结语
根据轨道不平顺输入数值算法,利用VC++和Matlab软件,为车辆工程专业学生设计了一套轨道不平顺数值输入仿真实验系统。该系统界面包括算法选择、数据参数输入、波形图和操作等操作区域,可以较好地模拟轨道不平顺输入信号的数值模拟过程,并且仿真精度较高。
