基于Matlab和双容水箱的现代控制理论实验设计
2019-06-18高宏岩郭春江
高宏岩, 郭春江
(山东科技大学 电气与自动化工程学院, 山东 青岛 266590)
现代控制理论实验通常采用Matlab仿真或自动控制原理模拟实验箱进行仿真,仿真实验无需建模,直接给出被控对象的数学模型,不利于学生对工程应用问题的理解。仿真实验具有灵活性和方便性等特点,但由于不是在真实实验设备中开展实验[1],学生无需考虑工程实现问题,不利于培养学生工程素养。因此,采用真实实验设备——双容水箱设备开发现代控制理论课程的状态反馈和内模控制实验项目,并在实验过程中借助Matlab软件设计控制器参数,既简化了实验的设计过程,也加强了学生工程实践能力的培养。
1 实验设备
利用浙江求是科教设备有限公司NPCT-Ⅲ型过程控制实验装置开展实验研究,该实验装置由被控对象﹑控制台和计算机组成[2]。本实验被控对象为上下串联的双容水箱,如图1所示。
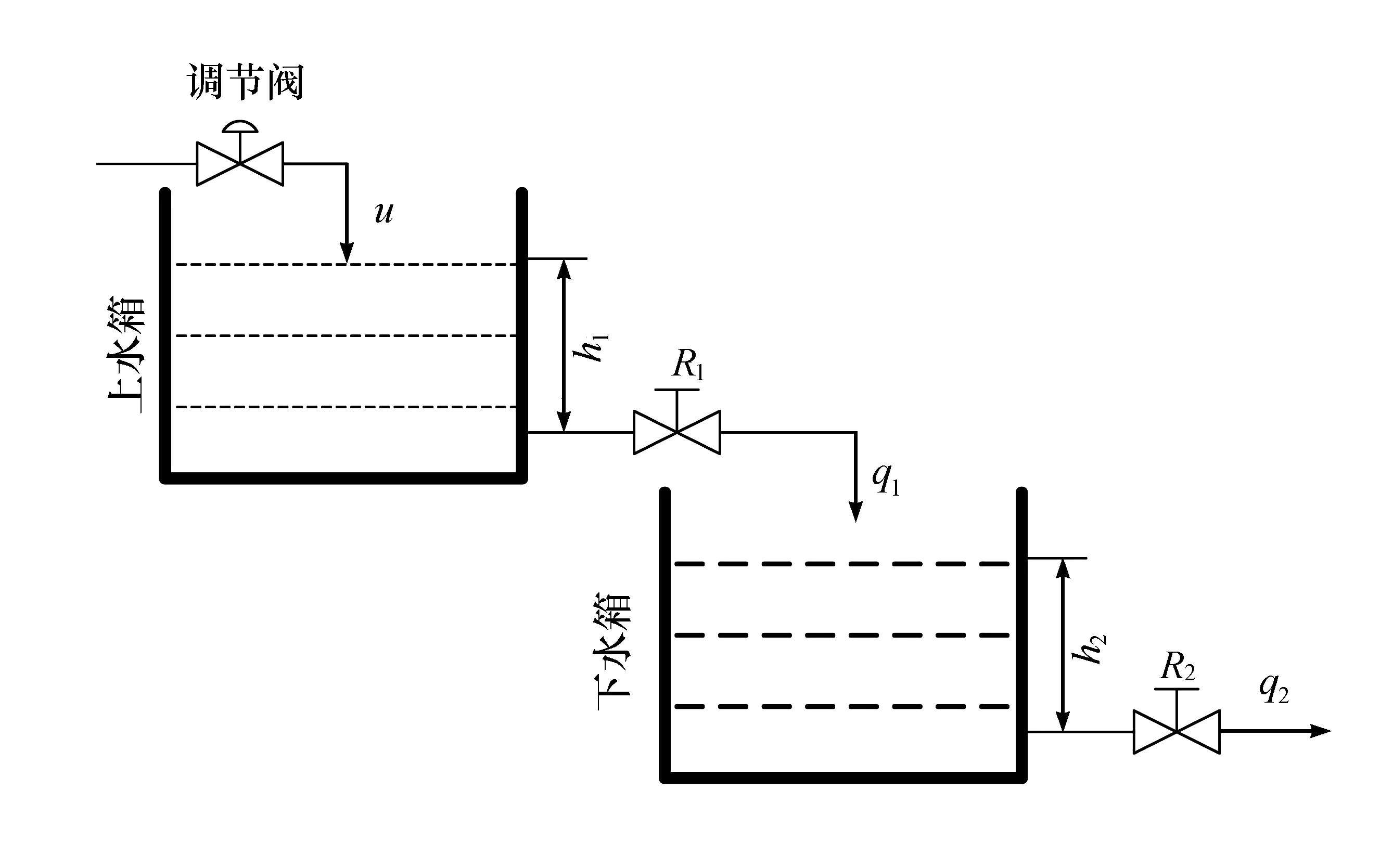
图1 双容水箱示意图
图1中h1﹑h2分别为上﹑下水箱液位;q1和q2分别为下水箱进水量和出水量;R1和R2分别为上﹑下水箱出口阀的液阻;下水箱液位h2为被控量,上水箱入口流量u为控制量[3]。控制系统硬件设备主要由液位变送器、数据处理模块、电动调节阀和上位计算机组成。上下水箱的液位变送器分别连接数据处理模块R-8017,电动调节阀连接数据处理模块R-8024,数据处理模块通过RS232串口通信方式与计算机连接。液位变送器采集的液位值经R-8017模块进行A/D转换后传输给计算机,在计算机组态王软件上编程实现控制算法或控制器功能[4];然后计算机将控制结果经R-8024模块进行D/A转换后作用到调节阀,通过改变调节阀开度改变控制量u,从而实现对液位h2的控制。
2 实验原理及设计步骤
2.1 状态反馈实验
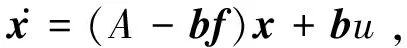
(1) 结合机理法和实验法建立双容水箱对象状态空间模型。根据物料平衡原理[5],单容水箱对象可以用一阶惯性环节表示,即上下水箱的数学模型用传递函数表示为G1(s)=H1(s)/U(s)=K1/(T1s+1),G2(s)=H2(s)/Q1(s)=K2/(T2s+1),其中K1=R1,K2=R2,T1﹑T2分别为上下水箱时间常数,模型参数K1﹑K2﹑T1﹑T2由实验法确定,根据G1(s)﹑G2(s)及H1(s)=R1Q1(s)传递关系,绘制双容水箱对象结构框图见图2。
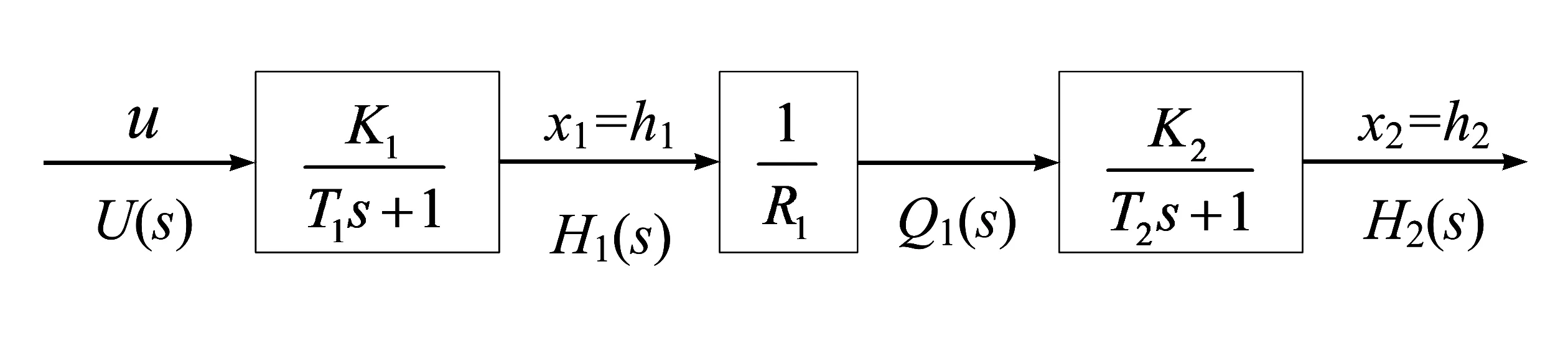
图2 双容水箱对象结构框图
选择上下水箱液位h1和h2作为状态变量x1和x2,由图2得到状态方程:
(1)
(1) 通过水箱特性测试实验确定模型中的参数K1﹑K2﹑T1﹑T2。在计算机上运行组态王软件[6],在监控界面上手动给定调节阀u=10%的开度,分别测试上下水箱液位特性,得到上下水箱液位特性响应曲线如图3和图4所示。
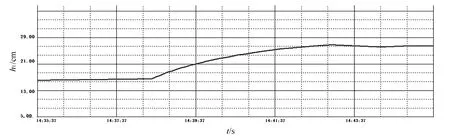
图3 上水箱液位特性响应曲线

图4 水箱液位特性响应曲线
由图3和图4分别求得放大系数K1=[y1()y1(0)]/u=0.796,K2=[y2()y2(0)]/u=2.327。通过两点法求时间常数:T1=35.25 s,T2=120.25 s。将求取的参数代入式(1)得到双容水箱对象的状态方程为
(2)
(2)判断系统是否满足状态反馈极点任意配置的条件。状态完全可控是状态反馈极点任意配置[7-8]的条件,根据公式(2)及可控性秩判据判断状态完全可控,则可以进行状态反馈极点任意配置。
(3) 确定期望极点和期望闭环特征方程D*(s)。控制系统性能指标要求超调量%≤10%,调节时间ts≤150 s,则根据二阶系统性能指标计算公式得阻尼比>0.59,自然振荡频率ωn>0.04 rad/s,实验中取阻尼比=0.7。考虑实际控制系统调节阀的动作范围在0%~100%之间,因此控制量u应被限制在调节阀动作范围之内,这样自然振荡频率ωn的可选值将受到约束。实验中取n=0.06 rad/s,得到期望极点和期望闭环特征方程D*(s)=(s1)(s2)。

(5) 根据D*(s)=D(s),计算状态反馈向量f=[f1,f2]。
(6) 计算误差补偿增益K。经状态反馈后闭环系统在单位阶跃信号作用下输出为
(3)
由终值定理求输出响应的稳态值c()为
c()
(4)
由此可见c()1,系统存在稳态误差。为了补偿稳态误差,在参考输入之后前置了误差补偿环节。其补偿增益K为
(5)
步骤(2)—(5)可以借助Matlab完成[9]。具体程序如下:
A=[-0.028 0; 0.024 -0.008];b=[0.023 0]′;c=[0 1];d=0; sys=ss(A,b,c,d) %状态空间模型
S=ctrb(A,b);r=rank(S); %求可控性判断矩阵的秩
P=[-0.042+0.043i; -0.042-0.043i]; %期望极点
f=acker(A,b,P) %求状态反馈向量f
K1=0.796;K2=2.327;K=(f(1)*K1+1+f(2)*K2)/K2%补偿增益K
经上述计算得到状态反馈向量f=[2.087 0,5.443 8],补偿增益K=6.587 5。
状态反馈实验中为了实现稳态误差补偿,前置了误差补偿环节,由式(5)可知,补偿增益K取决于水箱参数K1和K2。在建模过程中,参数K1和K2的求取不可避免存在误差,而且在水箱系统实际运行过程中参数K1和K2也可能发生变化。K1和K2建模误差或参数变化是无法预测的,故补偿增益K一旦设计好便不再改变,因此当参数K1和K2发生变化时是不能实现稳态误差全补偿,即控制系统不可避免存在稳态误差。
2.2 内模控制实验
上述单纯的状态反馈设计不能实现零稳态误差跟踪,因此研究基于内模原理[10]的状态反馈控制。它是在状态反馈系统的前向通道引入参考输入的内模,从而使系统输出能以零稳态误差跟踪参考输入信号。
2.2.1 内模控制实验原理

(6)

(7)
将式(6)和(7)构造增广系统方程

(8)
若增广系统可控,则可通过下述反馈使系统渐近稳定且以零稳态误差跟踪参考输入信号:
w=-h1e-h2z
(9)
对式(9)求积分得内模控制律为
(10)
2.2.2 内模控制设计步骤
内模控制设计步骤与状态反馈设计步骤[11]类似。
(1) 建立增广系统数学模型。根据式(2)和式(8)构造增广系统方程:
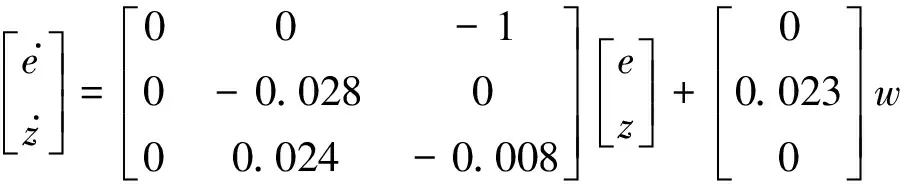
(11)


(4) 计算反馈后闭环特征方程D(s)。
(5) 根据D*(s)=D(s),计算反馈系数h1、h2和h3。

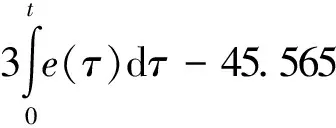
(12)
3 Matlab仿真实验
根据图2和实验原理,在Simulink中建立状态反馈和内模控制仿真实验(见图5),开展实验研究。
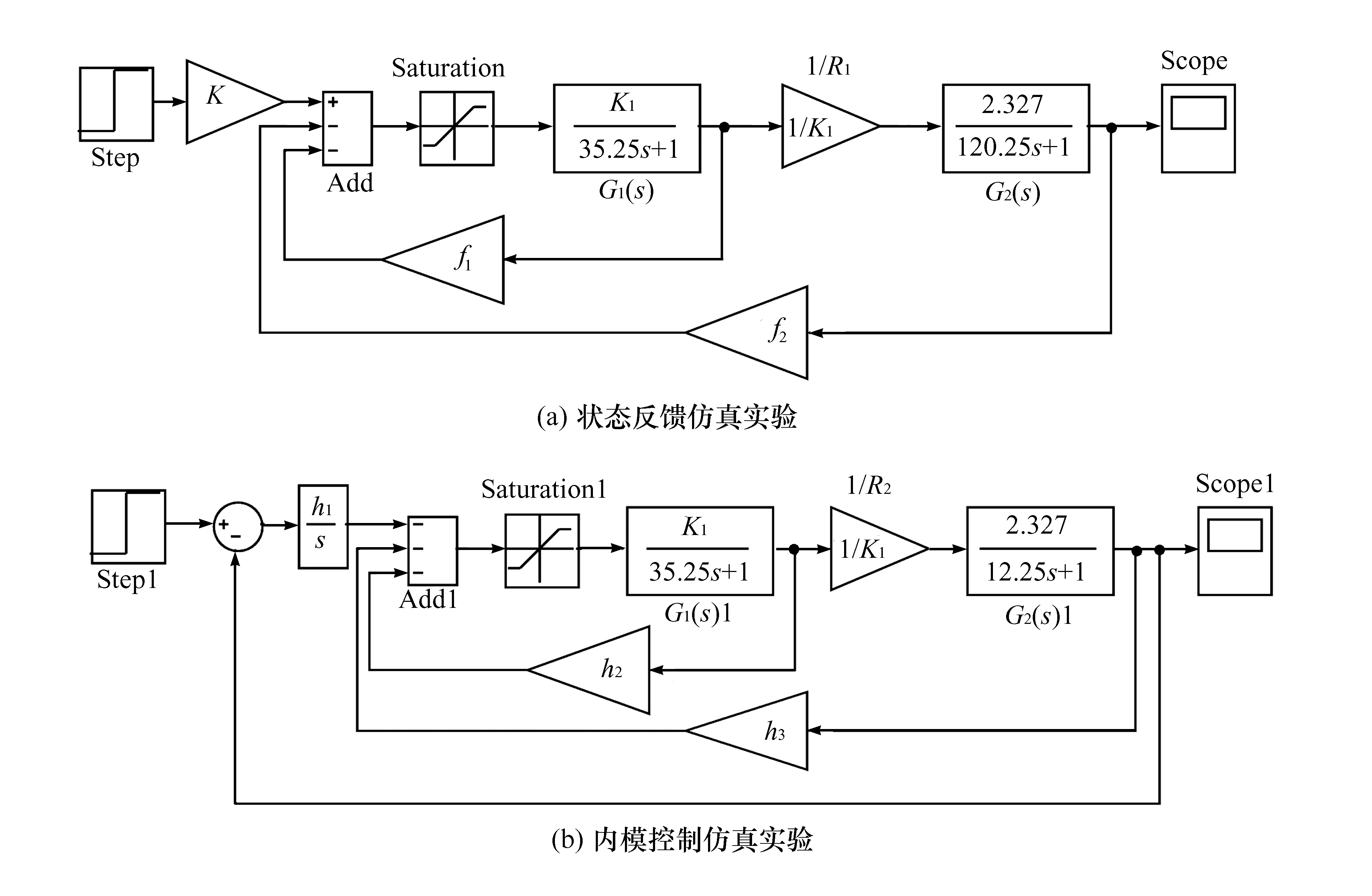
图5 Simulink仿真实验
水箱系统实际运行时,调节阀的开度在0%~100%之间变化,故在图5中加入了限幅环节[12],以限制控制量的变化范围。图5中参数K1分别取2个数值进行2次实验:第一次K1取建模结果数值0.796,第二次K1取1表示参数发生变化,即液阻R1变化。在输入端加入阶跃信号,在示波器上得到输出量的响应曲线如图6所示。图6表明,当参数发生变化时,状态反馈不能实现稳态误差的全补偿,而内模控制能够适应参数的变化实现零稳态误差跟踪。

图6 仿真实验结果
4 基于水箱设备的实物实验
在进行水箱设备接线、上电、开阀等准备工作后,在组态王软件中完成创建新工程、定义硬件设备、添加工程变量、制作监控画面和编写命令语言等工作,其中命令语言采用脚本程序实现状态反馈和内模控制算法。限于篇幅,以下只给出实现内模控制的脚本程序:
if(1)
{
\本站点a00=\本站点 k-\本站点液位2;
\本站点uk=\本站点h1*\本站点a00+\本站点uk11;
\本站点uk11=\本站点uk;
\本站点ek=\本站点uk-\本站点液位1*\本站点h2-\本站点液位2*\本站点h3;
if (\本站点ek<100)
{
if(\本站点ek<0)
{\本站点uk2=0; }
else
{\本站点uk2=\本站点ek; }
}
else
{\本站点uk2=100; }
}
运行组态王软件,在监控界面上施加给定值的阶跃扰动,在趋势曲线画面中观察到状态反馈和内模控制输出响应曲线如图7所示,可见两种控制均具有较好的动态性能。由图7(a)可知,状态反馈存在稳态误差,原因是实际运行参数与建模参数不一致,补偿增益K不能随参数变化而改变,说明状态反馈在参数变化时不能实现误差全补偿。由图7(b)可知,即使实际运行参数与建模参数不一致,内模控制依然能够实现对输入信号的无静差跟踪。
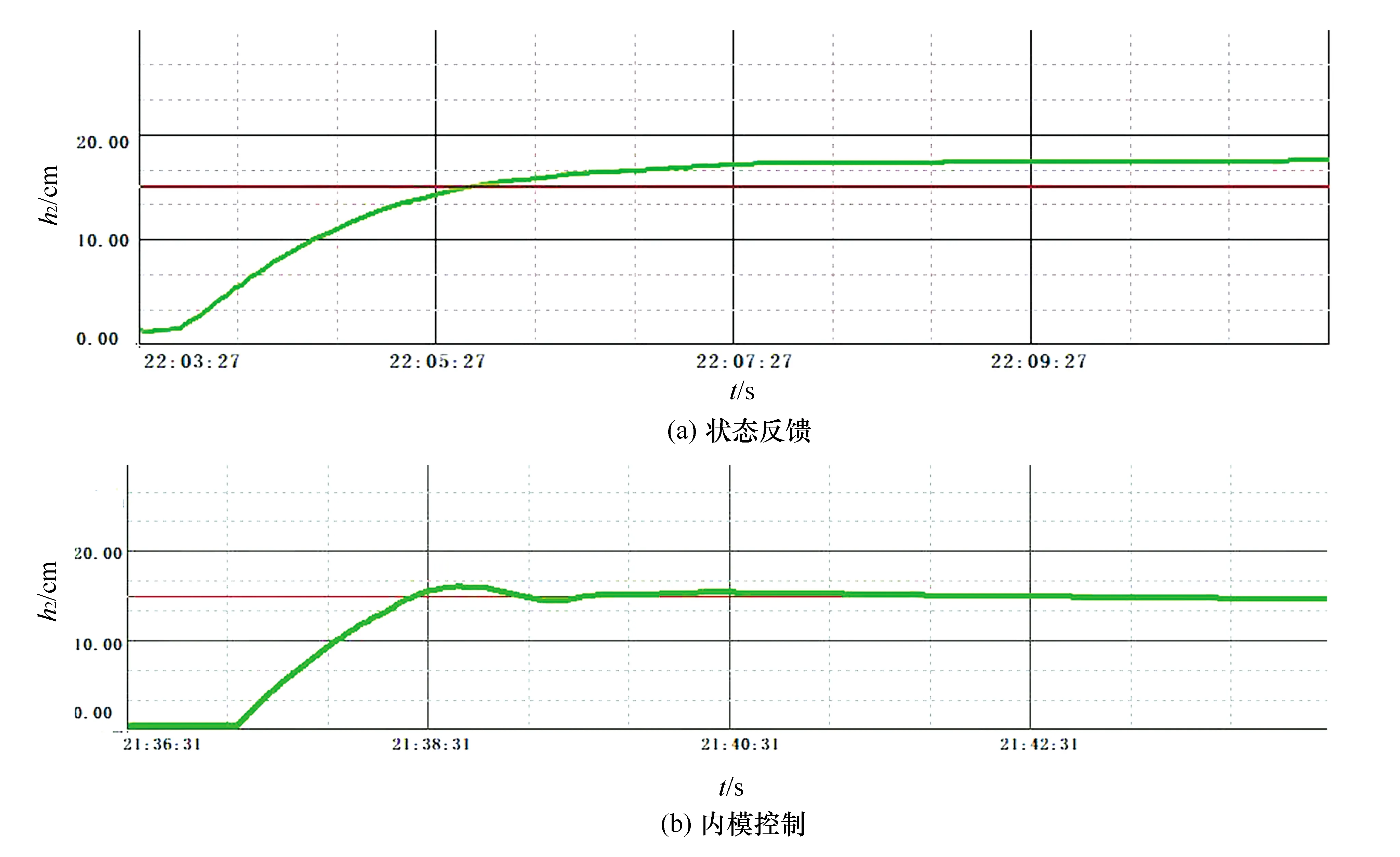
图7 基于水箱设备的实验结果
5 结语
Matlab仿真实验具有灵活性和便利性等特点,但它依赖于精确的数学模型;当对象参数变化等信息不能及时获取时,仿真实验难以模拟诸如参数变化等情况,并且仿真实验无需考虑工程实现问题。基于水箱设备开展实验研究,需要考虑执行器饱和、对象参数变化等工程问题。学生通过组态王软件完成工程创建、通信建立、变量定义、画面制作和程序编写等工作,使学生全面地掌握基于状态空间的控制系统设计和工程实现方法。
