基于T-S故障树的液压轮边制动系统可靠性分析
2019-06-17姚成玉1侯安农1陈东宁潘昊洋吕世君
姚成玉1, 侯安农1, 陈东宁, 潘昊洋, 吕世君
(1. 燕山大学河北省工业计算机控制工程重点实验室, 河北秦皇岛 066004;2. 燕山大学河北省重型机械流体动力传输与控制重点实验室, 河北秦皇岛 066004;3. 先进锻压成形技术与科学教育部重点实验室(燕山大学), 河北秦皇岛 066004)
引言
港口及大型铁路货场所用的起重机械设备大部分安装在空旷、风力极大的场所,会受到突发的阵风和台风的袭击。传统的港口起重机械防风装置多为夹轨器和顶轨器,通过一定的力直接作用在轨道上产生与风力反作用的摩擦阻力,从而实现抵抗风力的作用。液压轮边制动系统作为港口岸边装卸起重机械重要的防风装置,是通过对车轮施加一个足够的制动力矩,使起重机械在风力的作用下,车轮的滚动阻力增大直至打滑,从而产生滚动摩擦阻力或滑动摩擦阻力,用于起重机械工作状态和非工作状态下的防风制动[1]。
随着人们安全防范意识的提高,安全装置的稳定性和可靠性也越来越受到重视。由于液压轮边制动器属于安全装置,并且港口气候环境较为复杂,因此液压轮边制动系统性能的稳定性、使用过程中的可靠性十分重要[2]。董炜[3]分析了液压轮边制动器在岸桥中的防风效果,并且与传统的防风装置进行了对比,说明了液压轮边制动器的优越性。张诚龙[4]提出了液压轮边制动器在轨道式龙门起重机防风改造中技术方案,并进行了防风能力验算,提高了轨道式龙门起重机的防风性能。刘丽娜[5]通过建造传统故障树求解最小割集的方法分析液压轮边制动系统得出系统故障概率,为系统的维护和检修提供了依据。
实际工程中由于统计数据的不确定性、系统故障机理的不确定性等,可能导致不能用确定性理论来分析解决实际工程中存在的问题。凸集模型作为描述有界不确定信息的数学模型,可以将不确定事件的可能性用集合描述,区间模型就是其中最常用的方法之一。区间模型是描述不确定性问题的工具,是对传统的经典概率理论的推广,其实质就是将区间数应用于概率理论,将概率用区间数来表示,以处理系统中存在的模糊性和不确定性。目前,区间分析被广泛应用于可靠性理论中[6-7]。T-S故障树是用T-S门描述事件联系、利用T-S模型能够处理不确定信息的特性而构造的一种新型故障树。T-S故障树分析可以根据所给出的基础数据和所列出的T-S门规则表进行编程,直接求解系统故障概率,并且T-S故障树不仅可以描述传统故障树所能描述的失效机理,还可以描述传统故障树不能描述的失效机理,具有更好的适应性和灵活性[8]。将区间模型与T-S故障树结合,建造液压轮边制动系统的T-S故障树,并结合区间数据进行计算,求得系统的故障概率并得出各底事件的概率重要度和关键重要度,为液压轮边制动系统的可靠性分析提供更为全面合理的依据。
1 液压轮边制动系统原理
液压轮边制动系统工作原理如图1所示。
电磁换向阀在失电状态时,液压轮边制动器处于制动状态,车轮被夹紧;当司机发出“松轮”信号时,电动泵启动,电磁换向阀得电换向,由电动泵和蓄能器同时向液压轮边制动器液压缸提供液压油,推动活塞压缩碟形弹簧组,此时液压轮边制动器松开车轮,当系统压力达到压力继电器设定的上限值时,电动泵停止运转,系统处于保压状态,由蓄能器维持液压轮边制动器油缸压力,当压力下降到压力继电器下限值时,电动泵重新启动。当起重机械行走至指定位置时,电磁换向阀失电,液压轮边制动器中的液压油经电磁换向阀回流至油箱,碟形弹簧组复位夹紧车轮。在液压轮边制动器出口安装有单向节流阀,防止紧急制动对设备产生冲击。系统中手动泵可以在系统出现故障或断电情况下应急使用。
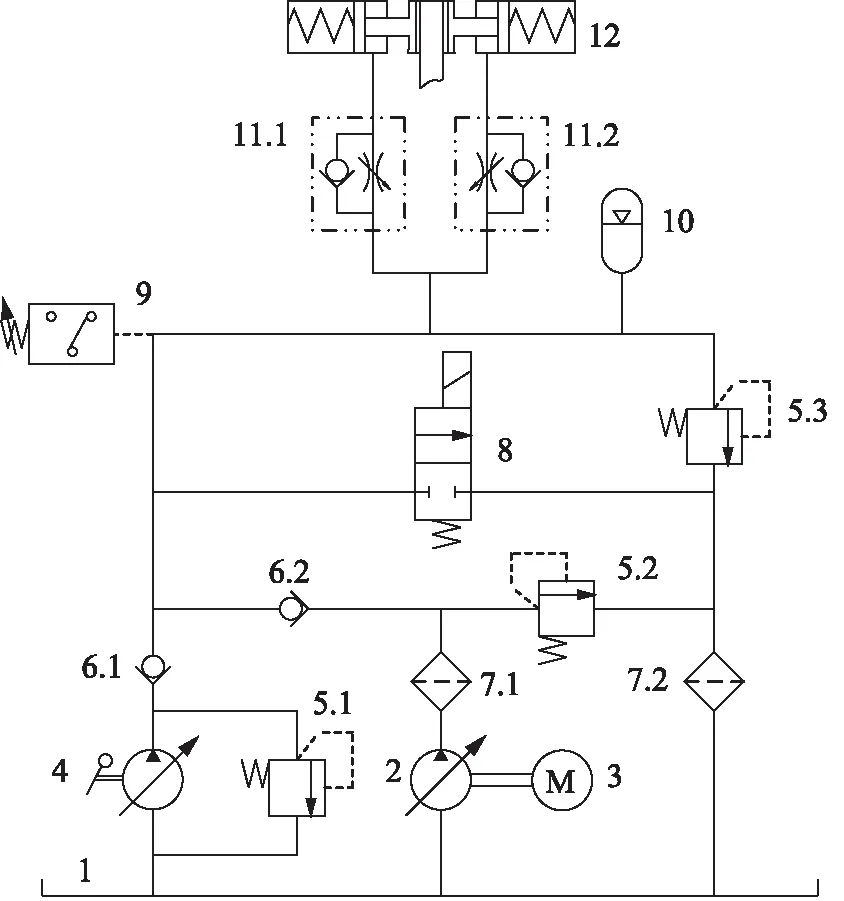
1.油箱 2.液压泵 3.电机 4.手动泵 5.溢流阀6.单向阀 7.过滤器 8.电磁换向阀 9.压力继电器10.蓄能器 11.单向节流阀 12.液压轮边制动器图1 液压轮边制动系统原理图
2 液压轮边制动系统T-S故障树
对于液压轮边制动系统而言,常见的故障主要有两种:一是轮边制动失效,即轮边制动器无法实施制动或制动力不足;二是液压轮边制动系统无法松闸。制动失效造成的事故危害极大,制动系统无法松闸直接影响主机的正常运行[5]。以液压轮边制动系统故障为顶事件建造T-S故障树,如图2所示。
图2中,顶事件y9表示液压轮边制动系统故障;中间事件y1~y8分别为液压泵源故障、液压油路故障、制动器液压缸有背压、活塞杆行程过大、制动器液压缸泄漏、液压站故障、制动器抱闸失效、制动器无法松闸。底事件x1~x18分别代表的故障模式及其失效率区间如表1所示。
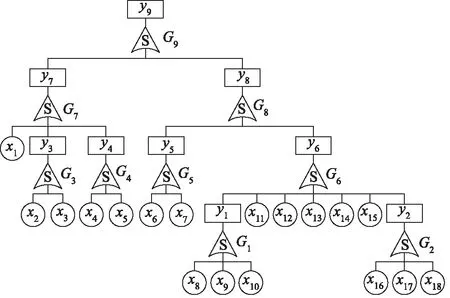
图2 液压轮边制动系统T-S故障树
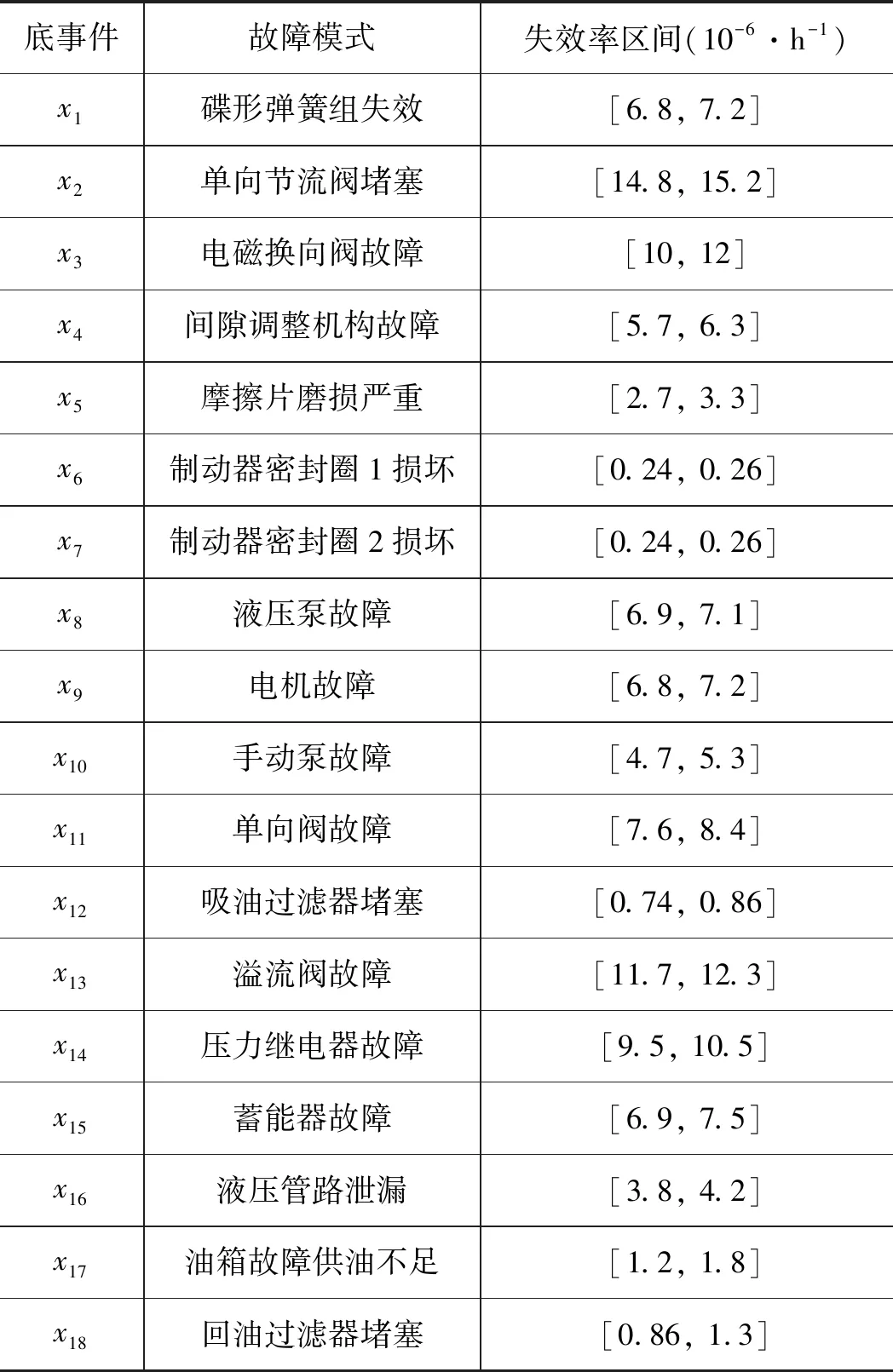
底事件故障模式失效率区间(10-6·h-1)x1碟形弹簧组失效[6.8, 7.2]x2单向节流阀堵塞[14.8, 15.2]x3电磁换向阀故障[10, 12]x4间隙调整机构故障[5.7, 6.3]x5摩擦片磨损严重[2.7, 3.3]x6制动器密封圈1损坏[0.24, 0.26]x7制动器密封圈2损坏[0.24, 0.26]x8液压泵故障[6.9, 7.1]x9电机故障[6.8, 7.2]x10手动泵故障[4.7, 5.3]x11单向阀故障[7.6, 8.4]x12吸油过滤器堵塞[0.74, 0.86]x13溢流阀故障[11.7, 12.3]x14压力继电器故障[9.5, 10.5]x15蓄能器故障[6.9, 7.5]x16液压管路泄漏[3.8, 4.2]x17油箱故障供油不足[1.2, 1.8]x18回油过滤器堵塞[0.86, 1.3]
根据实际情况,系统中每个部件都有正常和故障两种状态。除泵源系统部件外其他部件的故障都会直接影响系统正常运行,因而图2中的T-S门除G1门外均为或门。G1门、G2门的规则如表2和表3所示(0代表正常状态,1代表故障状态)。
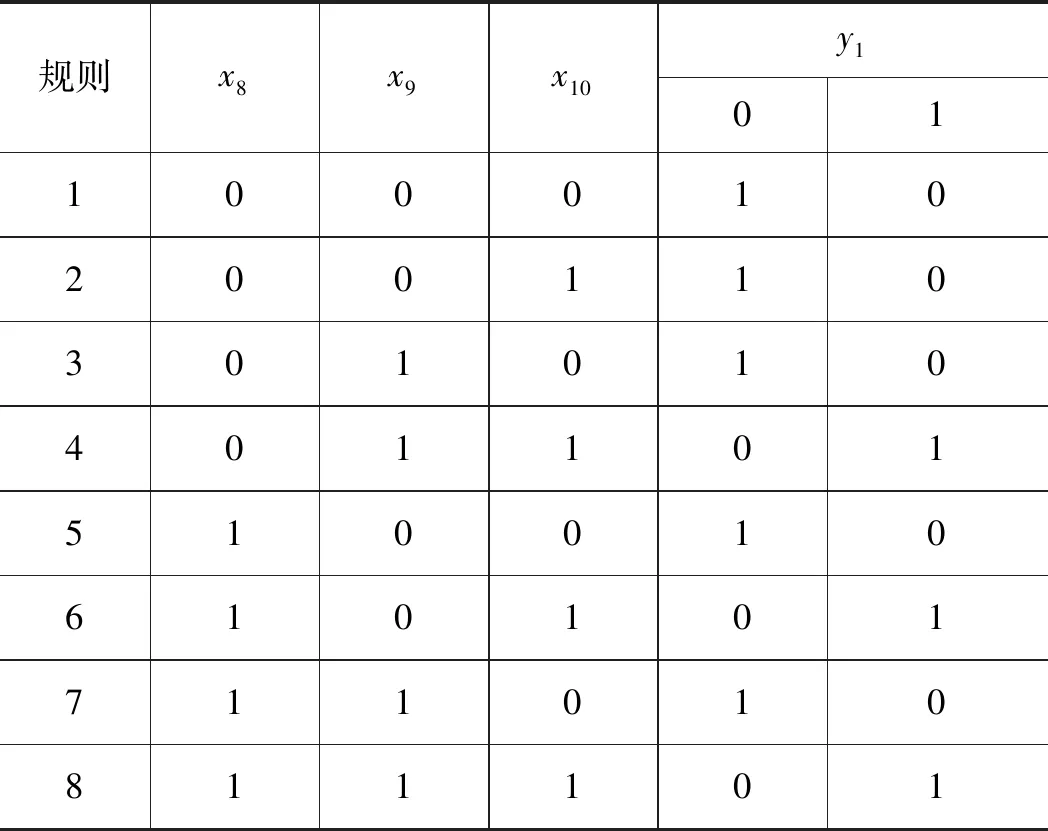
表2 G1门规则
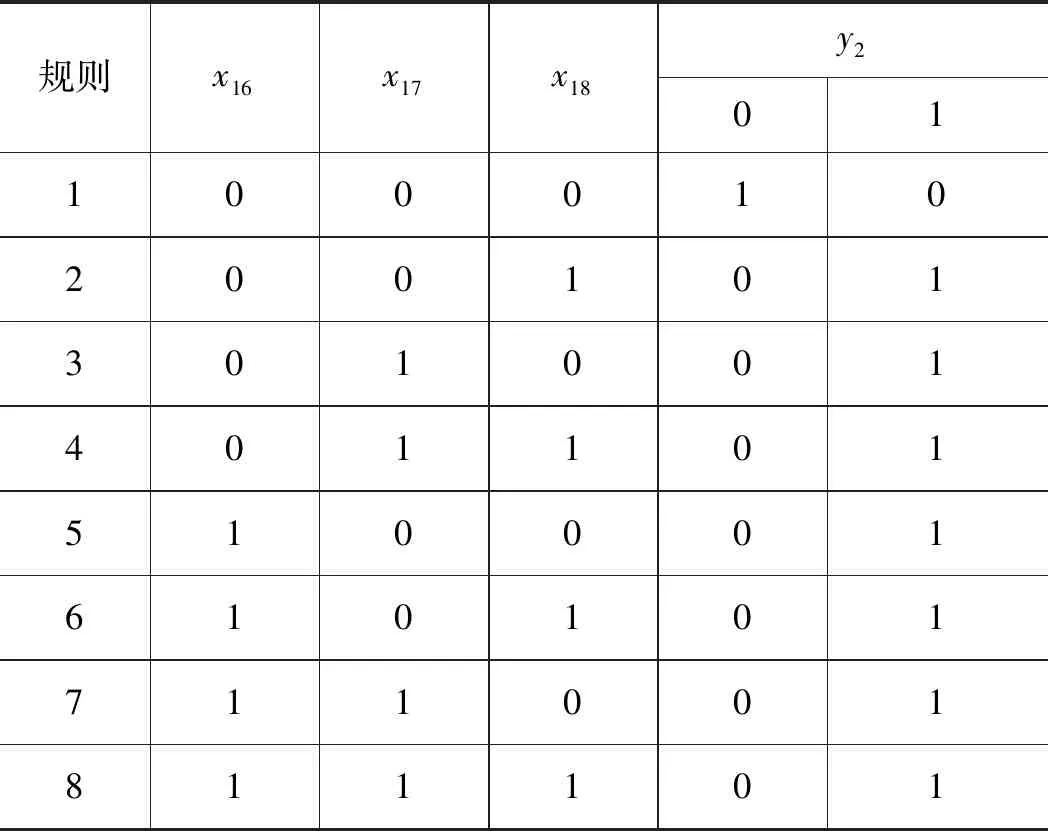
表3 G2门规则
3 液压轮边制动系统可靠性分析
根据所建造的T-S故障树,将区间模型引入T-S故障树分析,对液压轮边制动系统进行可靠性分析,求得液压轮边制动系统的故障概率区间、各底事件的概率重要度区间和关键重要度区间。
3.1 系统故障概率求解
在区间模型中,不确定性变量用一个具有上、下界的区间集合来定义[9-10]。区间变量X表示为:
X=[X(L),X(U)]={X∈RX(L)≤X≤X(U)}
(1)
式中,X∈R为实数集R中的有界闭区间变量;X(L)为区间变量的下界;X(U)为区间变量的上界,X(L),X(U)∈R,且X(L)≤X(U)。当区间数的上下界相等时,即X(L)=X(U),区间数则变为一个数值。
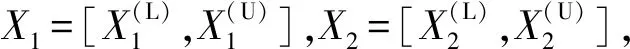
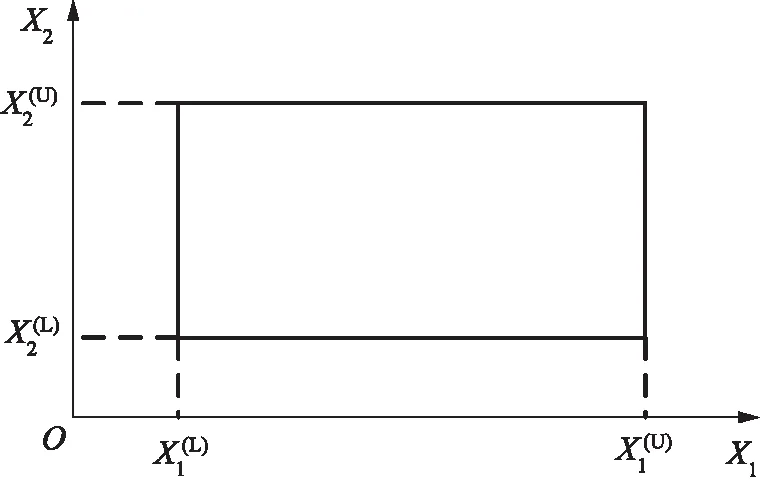
图3 二维箱体模型
区间的上下界是用一对实数表示的,使得它具有算术运算的性质,且区间运算仍然是封闭的[11]。因此,以下运算规则在区间模型中成立:
(2)
(3)
(4)
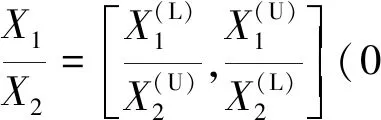
(5)
液压轮边制动系统每年的实际工作时间为t=300 h,若各底事件的寿命均服从指数分布,则底事件xi的可靠度与故障概率可由式(6)和式(7)求得:
Ri(t)=exp(-λit)
(6)
Fi(t)=1-Ri(t)
(7)
将区间模型引入T-S故障树分析,底事件的可靠度与故障概率可用式(8)和式(9)表示。
(8)
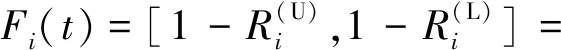
(9)
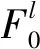
(10)
(11)
根据所建T-S故障树以及给出的基础数据,进行编程并计算,求得中间事件的故障概率区间如表4所示。

表4 中间事件故障概率区间
进而求得系统故障概率区间:
Fs(t)=[0.0242, 0.0273]
传统故障树求解顶事件故障概率需要求得系统顶事件故障的最小割集,最小割集为:{x1}、{x2}、{x3}、{x4}、{x5}、{x6}、{x7}、{x8,x10}、{x9,x10}、{x11}、{x12}、{x13}、{x14}、{x15}、{x16}、{x17}、{x18}。根据容斥定理求得系统故障概率区间Fs(t)为:
Fs(t)=[0.0242, 0.0273]
结果与T-S故障树相同,验证了所提方法的可行性,而T-S故障树无需求最小割集且计算更简便。
3.2 重要度分析
重要度分析是故障树分析中的重要组成部分,不同的底事件在系统中呈现非均等的重要性,底事件重要度不仅应用于系统可靠性分析,而且在系统设计优化、系统维护、故障诊断方案提出等方面有着重要的作用[12]。因此用重要度来衡量液压轮边制动系统各底事件的重要性对系统可靠性分析具有重要意义。
概率重要度表示因底事件状态变化而引起的顶事件故障概率变化的程度。假设系统由n个底事件组成,任意一个底事件xi的故障概率为Fi(t),系统顶事件故障概率为Fs(t),则底事件xi的概率重要度可定义为:
(12)
若顶事件的故障概率函数Fs(t)因系统较为复杂而难以确定,底事件xi的概率重要度可以利用式(13)计算:
(13)
式中,Fs[1i,Q(t)]为底事件xi故障条件下顶事件的故障概率;Fs[0i,Q(t)]为底事件xi正常条件下顶事件的故障概率;Q(t)表示除xi外的其他底事件的组合。
关键重要度表示任意一个底事件xi故障概率的变化率引起顶事件故障概率的变化率,可定义为:
(14)
对式(14)进行简化可以得到:
(15)
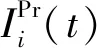
概率重要度能反映底事件的重要性,并为系统故障诊断中底事件的重要性计算提供了一种理论依据。关键重要度的意义在于通过改进系统最薄弱的环节以提高系统的可靠性。与概率重要度相比,关键重要度含有部件的概率重要度和其本身的故障概率两个方面。关键重要度不仅体现了部件在故障树中的地位,而且还体现了部件本身的故障概率,能更客观地体现部件对系统故障的影响。
根据式(13)、式(15),结合区间模型,求得各底事件的概率重要度区间、关键重要度区间如表5所示。
由表5中的重要度数据可以直观反映出在液压轮边制动系统中重要度较大的部件为单向节流阀、溢流阀、电磁换向阀和压力继电器,因此应重点对这几个部件进行检查和定期维护;针对系统中最关键的设备液压轮边制动器而言,其故障主要为单向节流阀堵塞、碟形弹簧组失效和间隙调整机构故障,可对这些零部件进行有针对性的优化改进以降低制动器故障概率,从而改善系统的可靠度。
4 结论
针对实际工程中故障数据不易精确获取的问题,将区间模型引入T-S故障树分析,解决了底事件失效可能性的不确定性问题;通过分析液压轮边制动系统原理及故障模式,对液压轮边制动系统进行建树分析,求得系统的故障概率区间和各底事件的概率重要度区间、关键重要度区间,为发现系统的薄弱环节、 缩短故
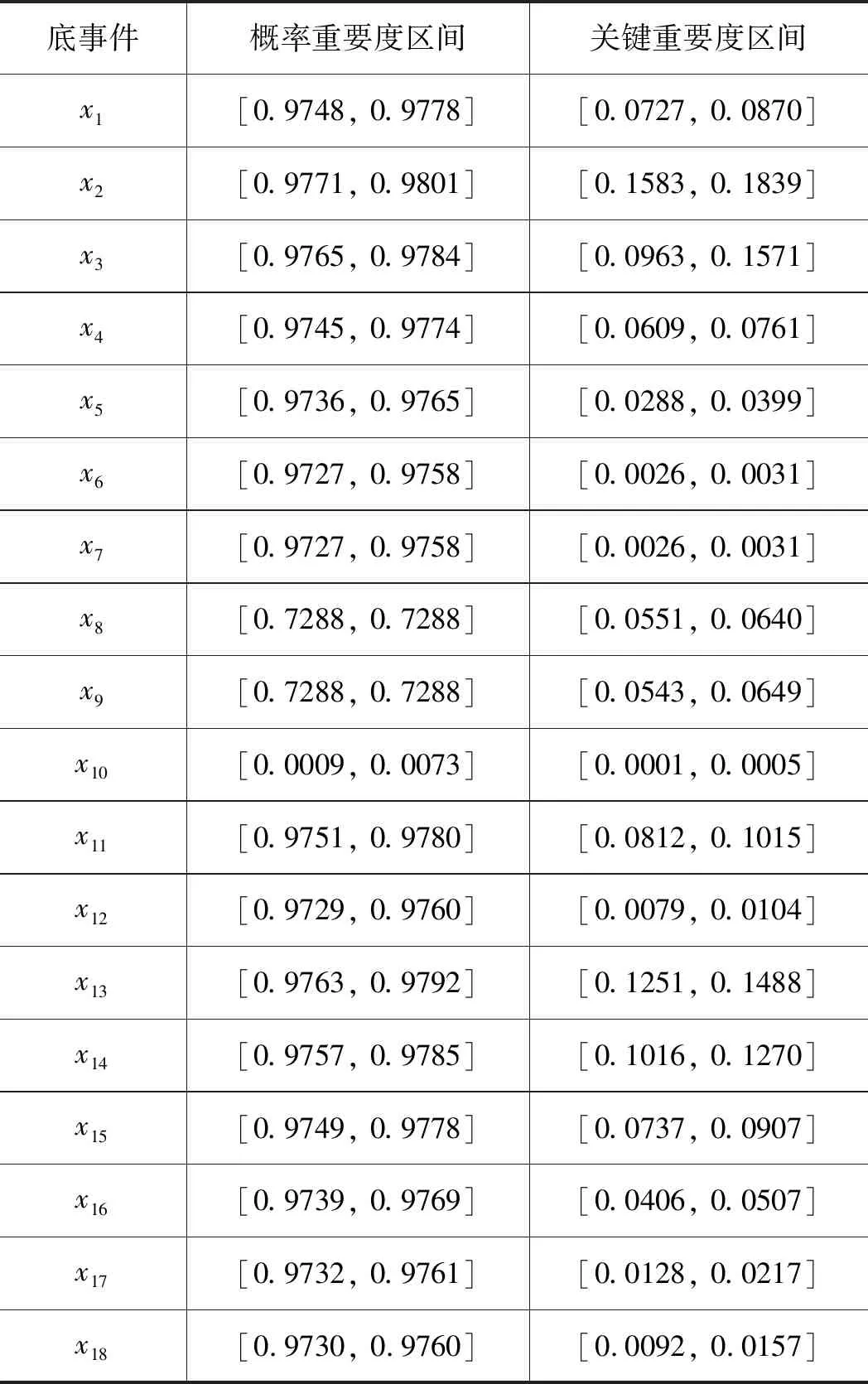
表5 底事件重要度区间
障查找与维修时间以及系统的优化改进提供了依据。
