基于消息传递的谱聚类算法

王丽娟 丁世飞 贾洪杰

（1.中国矿业大学计算机科学与技术学院，徐州，221116；2.徐州工业职业技术学院信息与电气工程学院，徐州，221400；3.江苏大学计算机与通信工程学院，镇江，212013）

引 言

聚类分析的一般过程是根据数据之间的相似度将其划分到不同的簇集中,使同一簇中的数据相似度较大,不同簇间数据的相似度较小。传统的聚类方法，如k-means算法等,缺乏处理复杂数据结构的能力,当样本空间非凸时,算法容易陷入局部最优[1]。

近年来,谱聚类由于其良好的表现,易于实现的特点,引起了学术界的关注[2]。谱聚类能在任意形状的样本空间上聚类,且收敛于全局最优,特别适用非凸数据集[3]。谱聚类算法将数据集中的每个点都作为图的顶点,任意两点之间的相似性值作为连接两顶点的边的权值,这样就构造了一个无向加权图。然后根据某种图划分方法将图分割为若干不连通的子图,子图中包含的点集就是聚类后生成的簇[4]。

传统的图划分方法有很多种,如最小割集法、比例割集法、规范割集法和最小最大割集法等[5]。通过最大化或最小化图割方法的目标函数得到最优割值,来获得聚类结果。但对于各种图分割方法来说,求目标函数的最优解往往是NP-hard的。根据瑞利熵理论,将原问题的离散最优化问题松弛到实数域,即可在多项式时间内解决[6]。对于图的划分,可以认为某个点的一部分属于子集A,另一部分属于子集B,而不是非此即彼。一般,在聚类过程中充分利用图的拉普拉斯矩阵的特征值和特征向量所包含顶点的分类信息,就可得到良好的聚类结果[7]。由于算法是基于矩阵谱分析理论来聚类的,因此称为谱聚类。目前,谱聚类已广泛应用在计算机视觉、数据分析、图像处理、视频监控以及自动控制等领域[8-10]。

谱聚类算法尽管在实践中取得了很好的效果,但是作为一种新型的聚类方法,仍处于发展阶段,还有很多问题值得进一步深入研究。例如,传统的谱聚类对初始值敏感,而且无法有效处理多尺度的聚类问题[11]。为了处理多重尺度的数据集,Zelnik-Manor等[12]提出了自适应的谱聚类。它不再指定统一的参数σ,而是根据每个点自身的邻域信息,为每个点xi计算一个自适应的参数σi,其中σi为点xi到其第p个近邻的欧式距离,该相似度度量称为自适应的高斯核函数。由于考虑了每个点邻域的数据分布,自调节的谱聚类能够有效分离出稀疏背景簇中包含的紧密簇。刘馨月等[13]通过局部密度获得数据中隐含的簇结构特征，再与自调节的高斯核函数结合，提出了一种基于共享近邻的自适应相似度的谱聚类算法。陶新民等[14]提出了一种在流形结构数据点间相似度计算方法,提高算法的聚类性能。为了解决传统谱聚类算法对尺度参数和聚类中心初始化敏感的问题,本文提出一种基于消息传递的谱聚类算法(Spectral clustering algorithm based on message passing,MPSC)。

1 谱聚类算法的初始化敏感分析

谱聚类算法是将数据聚类问题转化为图的最优分割问题。最小化或最大化图割方法的目标函数,均为NP离散最优化问题。幸运的是,谱方法可以为该最优化问题提供一种多项式时间内的宽松解[15]。这里的“宽松”指的是将离散最优化问题宽松到实数域,然后利用某种启发式方法将其重新转换为离散解。图分割的本质可以归结为矩阵的迹最小化或最大化问题,而完成该最小化或最大化的任务需要依靠谱聚类算法。

通常任何谱聚类算法都由3个部分组成：预处理、谱表示和聚类[16]。先构造相似图来描述数据集;然后建立相关的拉普拉斯矩阵,计算拉普拉斯矩阵的特征值和特征向量,基于一个或多个向量,把每个数据点映射到一个低维的代表点;最后,基于新的代表点,将数据点划分成两个或多个类。

在划分数据集或图时,有两个基本的方法：递归2-way划分法和k-way划分法[17]。递归2-way划分法是以一个层次的方式递归地调用2-way划分算法,当把图划分成两部分之后,再对子图应用相同的过程,直到聚类数目满足要求或不再符合递归条件为止;k-way划分法首先按照某种策略,将拉普拉斯矩阵的含有聚类信息的特征向量挑选出来,然后直接利用这些特征向量对数据集进行k-way划分。k-way划分的一个典型的谱聚类算法是由文献[18]提出的NJW算法。下面是汪中等[19]就谱聚类算法中初始值敏感进行的分析。

命题1设数据集X={x1,x2,…,xn}，以不同顺序输入得到的相似矩阵为W1,W2,对角矩阵为D1,D2,拉普拉斯矩阵为L1,L2,生成矩阵为Y1,Y2,则W1和W2相似,D1和D2相似,L1和L2相似,Y1和Y2相似。

证明：设数据集以x1,x2,…,xn的顺序输入得到矩阵W1，以xn,xn-1,…,x2,x1的顺序输入得到矩阵W2，矩阵W1经过若干次初等变换可得到矩阵W2,可证矩阵W1和W2相似。同理推出以任意顺序输入得到的矩阵W2均与W1相似。由于矩阵D1为对角矩阵,其主对角元素为相似矩阵W1的相应各行元素之和,故矩阵D1和D2相似。又因,且D1,D2为对角矩阵,由矩阵W1和W2相似、L1和L2相似,其对应的特征向量x1经过若干次初等变换可以得到特征向量x2，可证生成矩阵Y1和Y2亦相似。故结论成立。

由命题1可知,以不同的顺序输入数据点,得到的相似矩阵W和最终的生成矩阵Y都是相似的,所以谱聚类算法对聚类中心的初始化敏感,本质上是因为在最后聚类阶段使用了k-means算法。为了解决这个问题,将AP聚类中的“消息传递”机制引入到谱聚类中,用来确定聚类中心,以改善谱聚类算法的性能。

2 AP聚类算法

近邻传播(Affinity propagation,AP)聚类是文献[20]提出的一种新的聚类算法。AP算法不需要事先指定初始聚类中心。实验表明,AP算法具有很高的效率,例如,对数千个手写的邮政编码的图片,AP算法只花费5 min就可以找出能准确解释各种笔迹类型的少量图片,而k-means算法要达到同样的精度需要耗费500万年。

AP算法以数据点之间的相似关系矩阵S为基础,将S的对角线上的数值S(k,k)作为点k能否成为聚类中心的评判标准,这个值称作偏向参数,用p(k)表示。如若p(k)越小,则点k成为聚类中心的可能性就越小。然后通过在数据点之间传递消息,经过数次迭代来寻找最优的类代表点集合,使网络能量函数达到最小[21]。即有式中：n表示数据的个数；ci表示点i所在类的聚类中心点；S(i,ci)表示点i与聚类中心点ci之间的相似度。

在AP算法中数据点之间相互传播的信息有两种：一种信息被称为“吸引度”(Responsibility),简写为R;另一种信息被称为“归属度”(Availability),简写为A。

R(i,k)是数据点i向其备选代表点k发出的信息,定义为

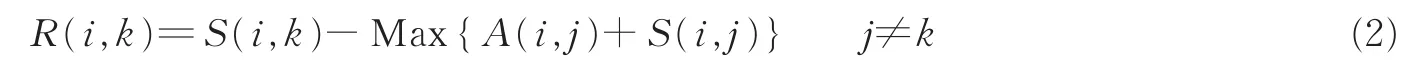
它反映了在考虑数据点i的其他备选代表点的情况下,数据点k点适合作为i点的代表点的累积证据。

A(i,k)是备选代表点k向数据点i发出的信息,定义为

它反映了在考虑了其他数据点是否选择点k作为自己的代表点的情况下,数据点i选择点k作为其代表点的累积证据。

R(i,k)与A(i,k)的和越大,则k点作为聚类中心的可能性就越大,并且i点隶属于以k点为聚类中心的聚类的可能性也越大[22]。这两种信息中包含了不同的竞争机制,在任何一个阶段根据这些信息可以判断出哪些数据点是代表点,以及每个数据点被划分到哪个数据类。

另外,为了平衡前后两次迭代的吸引度和归属度,AP算法引入了阻尼系数(Damping factor,即damp)来调整吸引度R(i,k)和归属度A(i,k),从而得到本次迭代最终的吸引度和归属度

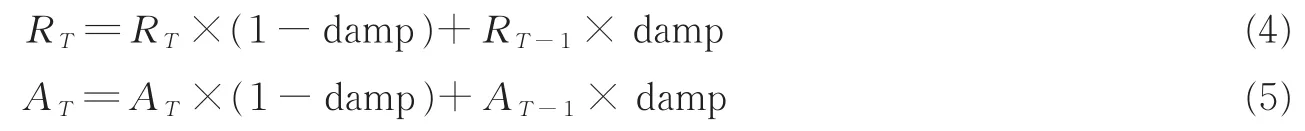
式中：RT-1,AT-1表示第T-1次迭代的吸引度和归属度;RT,AT表示第T次迭代的吸引度和归属度;阻尼系数damp的取值范围是[0.5,l)。

AP算法聚类的过程如图1所示,从图中可以看到n个样本点x1,x2,…,xn,初始时都被当作潜在的聚类中心。AP算法在迭代过程中,根据相似关系矩阵S(i,i)不断更新每个点的吸引度和归属度值,并且在网络节点之间不断地传递这两个信息量,直到产生m个高质量的聚类中心为止(满足停止条件)。

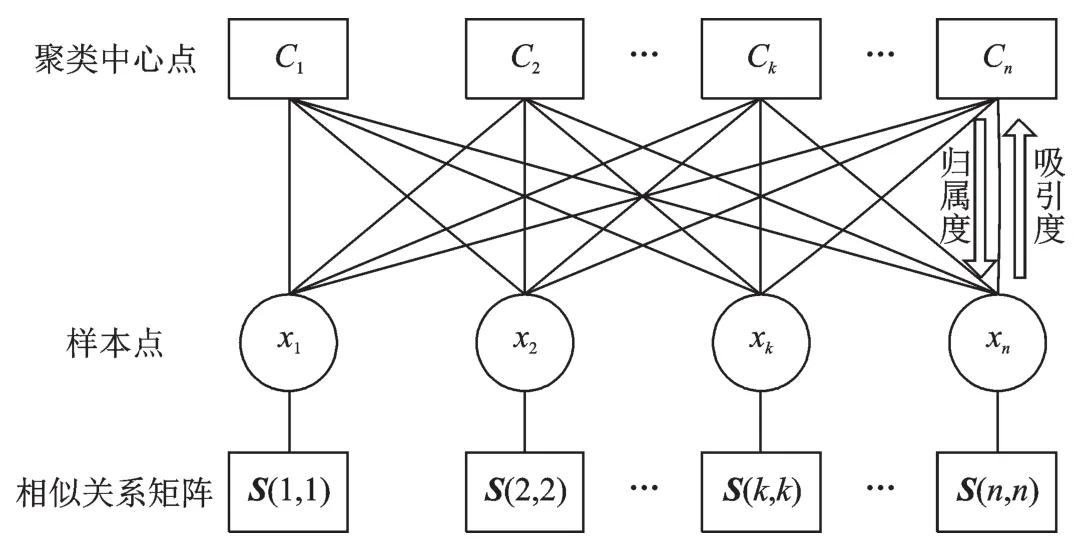
图1 AP算法聚类过程Fig.1 Clustering process of AP algorithm

3 本文算法

谱聚类的关键是选择一个恰当的距离度量方法,将数据集的内在结构真实地描述出来。相同类中的数据点应该具有较高的相似性,并且要保持空间一致性。因此相似矩阵的构造非常重要,其优劣会在很大程度上影响谱聚类的性能[23]。度量数据点相似性的方法常用高斯核函数，但是在高斯核函数中,尺度参数σ通常是固定的,这样两个数据点之间的相似度只取决于它们的欧氏距离,而对其周围的点没有适应性[24]。当处理复杂数据集时,简单的基于欧氏距离的相似性无法准确地反映数据的分布情况,会显著降低谱聚类的性能,导致较差的聚类结果。

Yang等[25]提出了基于密度敏感的相似性度量方法,该方法可以处理多尺度的聚类问题,还相对对参数选择不敏感。实验证明该算法能有效地描述数据的实际聚类分布。

定义一个密度可调节的线段长度

式中：d(xi,xj)为数据点xi和xj间的欧式距离,ρ＞1称为伸缩因子。

数据点xi和xj间的密度敏感的距离定义为

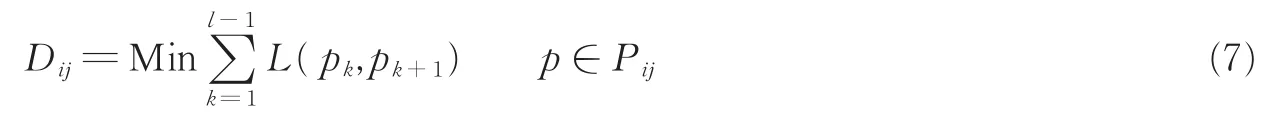
密度敏感的相似性度量可表示为

与高斯核函数相比,该相似性度量不需要引入核函数,可以在距离测度上直接计算相似度。密度敏感的距离可以度量沿着流形上的最短路径,使得位于同一高密度区域内的两点可用许多较短的边相连,而位于不同高密度区域内的两点要用穿过低密度区域的较长边相连,最终达到这一目的：使不同高密度区域的数据点间距离放大,同一高密度区域内的数据点间距离缩小。因此,这一距离度量是数据依赖的,且可以反映数据的局部密度特征,即所谓的密度敏感。

在上述相似性度量方法的基础上,将“消息传递”机制引入到谱聚类中,提出了一种基于消息传递的谱聚类算法(Spectral clustering algorithm based on message passing,MPSC),其基本思想是：首先使用基于密度敏感的相似性度量方法计算相似性，构造相似性矩阵和拉普拉斯矩阵;然后选择拉氏矩阵的前k个最大特征向量,构造特征空间并将原始数据集中的点映射到Rk空间中;最后在Rk空间中,用AP聚类方法将数据点划分成k个类。MPSC算法的详细步骤如下。

输入：数据集X={xi|i=1,…,n},聚类数目k。

输出：k个划分好的类。

Step 1根据式(8),计算数据点之间的相似性值,建立基于密度的相似性矩阵W∈Rn×n。

Step 2建立图的度矩阵D∈Rn×n,D是一个对角矩阵：对角线上的元素为称为顶点i的度,而对角线外的元素值为0。

Step 3根据相似性矩阵W和度矩阵D,构造拉普拉斯矩阵L：L=D-1/2WD-1/2。

Step 4计算矩阵L的前k个最大特征值所对应的特征向量u1,…,uk(重复特征值取其相互正交的特征向量),然后将这些特征向量纵向排列,形成矩阵U，U=[u1⋮…⋮uk]∈Rn×k。

Step 5规范化矩阵U的每一行,将行向量转变成单位向量,得到矩阵

Step 6将矩阵Y的每一行看作空间Rk中的一个点,利用AP聚类方法将这些点划分成k类。

Step 7如果矩阵Y的第i行被分配到第j类,就将原始的数据点xi划分到第j类。

MPSC算法继承了AP聚类的优点,它在初始时将所有的数据点都看作候选聚类中心,在不断的迭代过程中,选择某个数据点作为中心或每个数据点通过“消息传递”来竞争成为聚类中心,最终获得若干个优化的聚类中心。为了克服传统划分算法中随机选择参数对整个数据聚类结果的影响,引入消息传递机制优化传统谱聚类算法中初始化敏感的问题,得到更稳定的聚类结果。

4 实验分析

4.1 仿真数据集聚类

文献[26]给出了一些有“挑战性”的人工数据集,例如：Blobs and circle，Four lines,Two moons,Two circles,Two spirals和Three circles。用MPSC算法分别对这些数据集进行聚类,得到的聚类结果如图2所示(伸缩因子ρ=2,偏好参数p取数据集全体样本相似度的中位数)。从图2中可以看出,MPSC算法可以有效识别不同尺度的流形数据结构,得到令人满意的聚类结果。这是因为该算法采用密度敏感的相似性度量方法,通过拉普拉斯变换,将原始数据点映射到谱空间,使得相同类内的数据点更加紧凑,而不同类间的数据点更加分离。在2002年，Ng,Jordan和Weiss提出NJW算法（算法以3位作者名字的首字母缩写命名），图3给出了NJW算法（分别取σ=0.1和σ=0.2）在Blobs and circle,Two moons和Two spirals人工数据集上的聚类结果,可见NJW算法对尺度参数σ的取值比较敏感,当数据结构复杂时,无法得到准确的聚类结果。相比之下,MPSC算法在聚类过程中可以保持数据的全局一致性,从而克服了高斯核函数无法处理多尺度数据集的缺点。图2，3中横纵坐标分别为人工数据集的第1列和第2列。

图2 MPSC算法在人工数据集上的聚类结果Fig.2 Clustering results of MPSC algorithm on artificial data sets

4.2 真实数据集聚类

为了进一步验证MPSC算法的有效性,从UCI机器学习数据库中选取了3个真实的数据集,它们的数据特征如表1所示。如果将聚类得到的结果和真实的划分情况进行比较,对于数据集中的每对数据点,存在着下面4种可能：(1)SS：属于同一类的两个数据点在聚类时也被分到相同的类中;(2)SD：属于同一类的两个数据点在聚类时却被分到不同的类中;(3)DS：不属于同一类的两个数据点在聚类时却被分到相同的类中;(4)DD：不属于同一类的两个数据点在聚类时也被分到不同的类中。

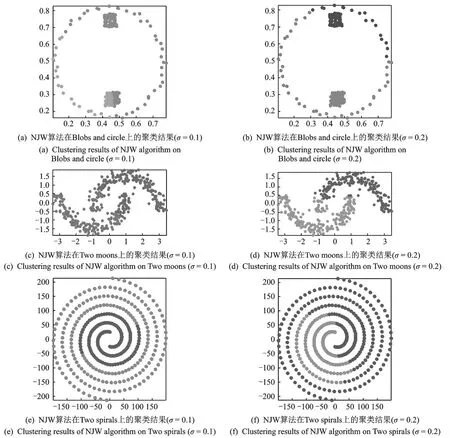
图3 NJW算法在人工数据集上的聚类结果Fig.3 Clustering results of NJW algorithm on artificial data sets

ARI(Adjusted rand index)指标就是根据数据点对的这4种关系来评价聚类结果的,它可以定量描述聚类的质量,客观反映聚类算法的优劣,是一种常用的聚类评价准则[27]。

设满足SS,SD,DS,DD关系的数据点对的数目分别是a,b,c,d,则ARI的计算公式为

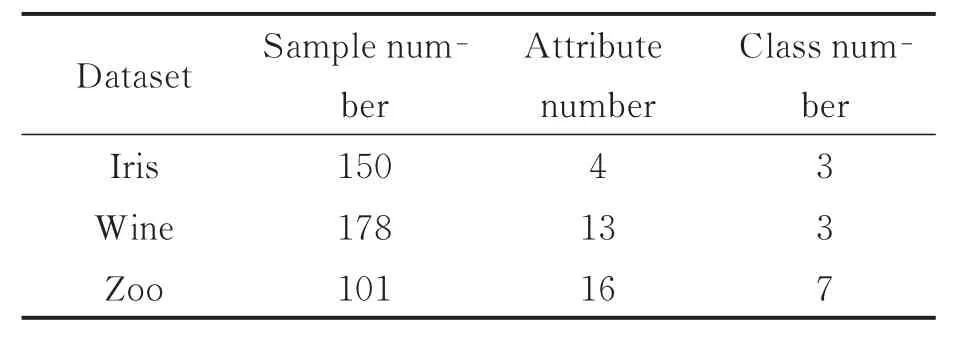
表1 真实数据集的数据特征Tab.1 Data characteristics of real data sets

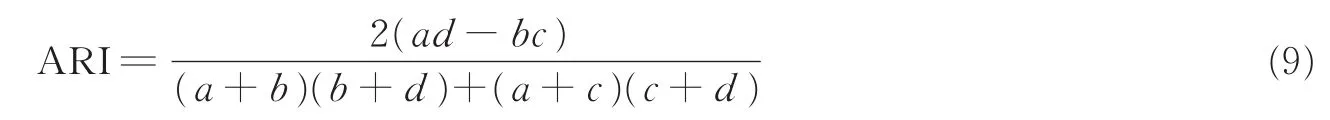
式中ARI∈[0,1],如ARI的值越小,也就表明聚类的结果越差。

在实验中,以ARI指标作为衡量标准,分别在Iris,Wine,Zoo数据集上,对比了MPSC算法、NJW算法、AP算法和k-means算法的聚类性能。实验结果如图4所示。

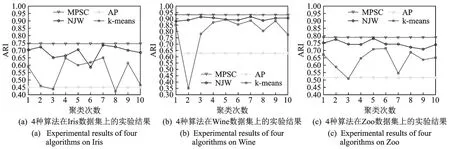
图4 4种算法在真实数据集上的实验结果Fig.4 Experimental results of four algorithms on real data sets

在图4中,NJW算法和k-means算法的曲线都有明显的波动,说明它们对聚类中心的初始化比较敏感。这两种算法都需要随机地确定初始聚类中心,当聚类中心的选择不合适时,就会产生较差的聚类结果。AP算法和MPSC算法的曲线非常平稳,没有出现任何波动,说明AP算法和MPSC算法的性能很稳定，但AP算法表现不理想，本文提出的MPSC算法将AP算法中“消息传递”机制引入，以确定聚类中心,有效地解决了传统谱聚类算法对聚类中心初始化敏感的问题。而且从图4中也可以看出,MPSC算法的ARI指标也要明显优于NJW算法、AP算法和k-means算法,因此MPSC算法可以得到比较理想的聚类结果。表2给出了MPSC算法、NJW算法、AP算法和k-means算法10次聚类的平均准确率和ARI指标。

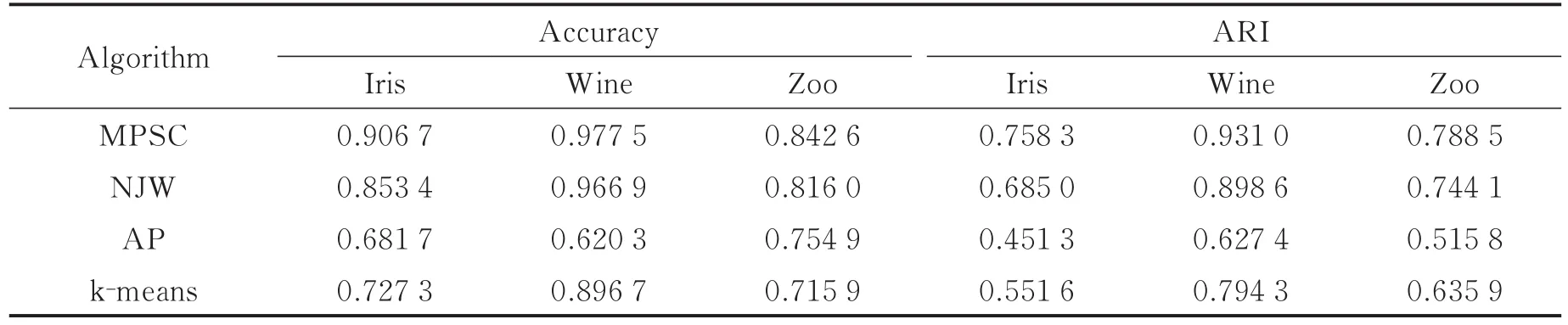
表2 4种算法的平均准确率和ARI指标Tab.2 Average accuracy and ARI index of four algorithms

5 结束语

本文分析了传统的谱聚类算法初始化敏感的原因,提出了一种基于消息传递的谱聚类算法。该算法引入了“消息传递”机制,通过在数据点之间不断传递“吸引度”和“归属度”信息,可以获得高质量的聚类中心。而且该算法使用了密度敏感的相似性度量方法,这样在度量数据点之间的相似性时,可以更好地描述数据的分布情况,保持数据的全局一致性。为了验证MPSC算法的有效性,在人工数据集和真实数据集上分别进行了仿真实验。实验结果表明,MPSC算法不仅可以有效识别数据全局的和局部的分布特征,而且对聚类中心的初始化不再敏感,其聚类准确率和稳定性都明显好于传统的谱聚类算法和k-means算法。

不过MPSC算法的计算复杂度较高,在处理大数据集时,会花费较长的时间,如何降低算法的时间复杂度,提高聚类的效率,还有待进一步研究。现实的聚类问题中,除了含有大量无标记的数据,有时也会含有一些标记数据,因此将半监督学习与MPSC算法相结合,利用少量的标记信息来指导聚类的过程,也是一个有价值的研究方向。另外,MPSC算法也有着广阔的应用前景,可以用来处理图像分割、语音分离和文字识别等实际问题。