空间点模式分析在野生动物危害研究中的应用

沈 拓 陈文汇/ 文

一、引言

野生动物危害问题由来已久。近年来，由于城镇化及工业化带来的人类土地利用需求的不断增加，野生动物的栖息地、生境及食物来源受到不同程度的威胁，进而导致人与野生动物冲突的不断加剧。城乡与森林交错地带为野生动物危害高发区域。以北京市为例，野生动物危害主要集中在延庆、门头沟、昌平、密云、怀柔、平谷和房山等七个地区。受损区域主要集中在乡镇及村庄，面积逐年扩大，损失及补偿额度逐年增加。研究野生动物危害的空间分布规律，对制定科学有效的防控措施具有很大价值，在有效减少野生动物危害区域人民生命财产损失的同时，能够兼顾生物多样性保护。

类似于犯罪及流行病学研究，野生动物危害事件可以抽象为空间中的点。空间点模式分析主要针对这些具有不同分布位置的点集进行点模式描述及点模式分析。空间点模式作为空间统计学的一个研究方向，最早可追溯到John Snow 针对伦敦霍乱的研究。空间统计学，经20 世纪60 年代计量革命的推动，获得了长足进展。继空间连续数据分析技术在地统计学（Matheron，1962）及空间格数据分析技术在社会经济学领域（Cliff and Ord，1981）的成功运用，Diggle 于1981 年率先将空间点模式方法应用于生态学领域。自此，国内外许多学科在研究中开始运用空间点模式分析方法。Khaemba 运用空间点模式方法分析了肯尼亚不同野生动物种群的分布模式。迟文学等在新生儿出生缺陷研究中，运用核函数估计等空间热点探测方法，发现了发病率与致病因素间的空间联系。李珊珊等运用以样方分析为主的点模式分析方法，研究了汶川震后滑坡数据的空间聚集性，结果表明震前与震后研究区域内的滑坡均呈聚集分布。Hosseinalizadeh 等对伊朗Golestan 省土壤管道侵蚀的空间分布特征进行分析，指出不同环境因素对管道侵蚀聚集的影响程度。

目前，国内野生动物危害的研究重点主要集中在野生动物管理及野生动物危害补偿两个方面，研究内容多为野生动物危害受损情况描述及相关政策法规的制定。针对偏远山区及保护区以外，尤其是城市边缘野生动物危害的空间格局研究甚少。为此，本文运用空间点模式分析方法，借鉴其他领域空间点模式研究成果，对密云野生动物危害数据进行分析，得出有关结论。

二、研究区概况

密云区地处北京市东北部，地理坐标116°39′～117°30′E，北纬40°13′～40°47′N，其面积为2229.45 平方公里，地形以山地为主，森林覆盖率达72.5%，动植物资源丰富，人口约42.8 万，其中农业人口约占60.3%。密云区以山地为主，农业人口占比高，是历年野生动物危害的多发区县。野生动物危害的受损对象以农作物为主，危害物种为野猪、獾等。

本文所使用研究数据来自北京市野生动物补偿管理平台2011- 2016 年密云区野生动物危害记录。每条记录包含危害发生的经纬度、时间、受损农作物种类以及受损状况描述信息，其中危害发生时间精确到小时，共计7456 条记录。

三、研究方法

1. 最近邻指数

最近邻指数是基于距离的二阶空间属性。野生动物危害最近邻距离计算每一个野生动物危害点和其最邻近的点的距离的均值，进一步将该值与随机分布下的最近邻距离进行比较来判断野生动物危害点的分布格局的分布情况。最近邻指数公式如下：

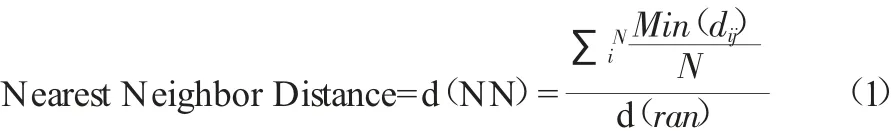
其中d（NN）为最近邻距离，N 为野生动物危害样本数目，dij为野生动物危点i 与点j 之间的距离。d（ran）为野生动物危害点在随机分布下的平均距离，其公式为：

其中A 为研究区域面积。当NNI 指数大于1 时，野生动物危害点呈离散分布，当NNI 小于1 时野生动物危害点呈聚集分布。并且可进一步通过检验来验证其可靠性，采用的z 检验公式如下：

2. Ripley's L 统计量

野生动物危害事件的分布往往随空间格局变化而呈现截然不同分布格局，针对这种情况，Ripley's K 统计量成为分析野生动物危害事件空间格局的有效工具。K 统计量定义如下：

其中N 为野生动物危害事件数目，A 为研究区域面积，tij是以某一野生动物危害事件点i 为圆心、ts为半径的圆内其他野生动物危害事件j 的发生次数。

在Crimestat 等软件中通常对K 统计量进行线性变换，以L函数的形式展示野生动物危害事件的空间聚集情况。L 函数的形式如下：

对不同空间距离ts比较与随机分布条件下的期望值可以确定野生动物危害事件的空间聚集情况，其中的置信区间通过蒙特卡洛模拟方法求得，模拟次数则根据实际情况设置。

3. 核密度估计

核密度估计作为一种热点探测的方法，不同于克里金插值法，适用于在空间中不连续分布的野生动物危害点集的研究。通过在每一野生动物危害点处建立核函数，获取整个区域内野生动物危害面状分布，进而将野生动物危害空间分布规律在地图上平滑地展示出来。核函数有多种形式，其中最常用的为高斯正态分布函数，其形式如下：

式中dij表示以xj为中心、带宽h 为半径的圆中第i 个点与xj的距离。根据以往研究，相比于函数的形式，带宽h 值的选取更为关键。带宽越小，核密函数反映的细节越详细，地图上的热点区域越明显；带宽越大，热点区域过渡相对平滑，制图效果较好。在实践中，h 最佳值的获得取决于多次实验的结果。

四、结果与分析

1. 最近邻指数

针对野生动物危害存在的边缘效应，我们在最近邻距离指数计算中采用了了矩形校正及圆形校正，密云野生动物2011- 2016 年最近邻指数结果如附表所示。

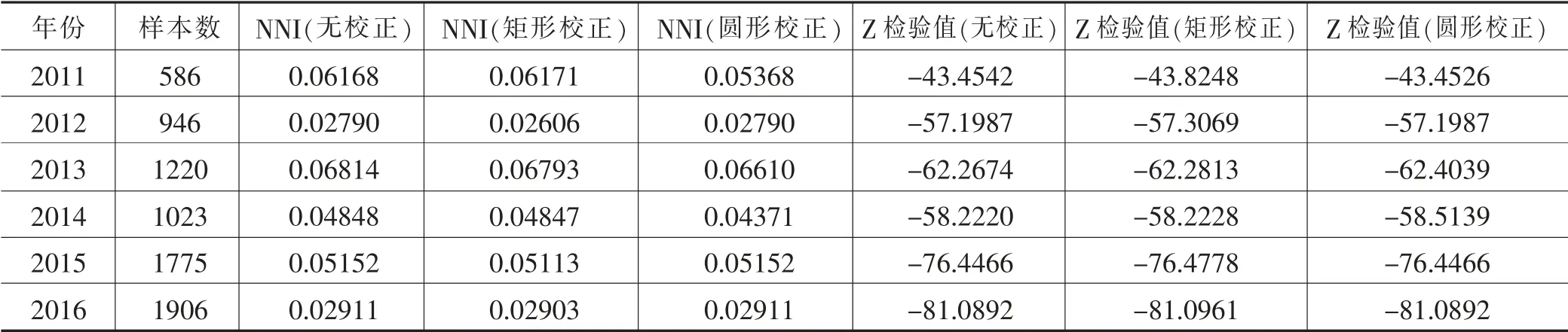
附表 密云区野生动物最近邻指数

密云野生动物最近邻指数表明，各年份野生动物危害均呈聚集分布，且通过Z 统计量显著性检验。其中2012 年和2016年野生动物危害聚集程度较高，其他年份则相对较低。从时间发展来看，自2013 年以来，密云野生动物危害的聚集程度逐年增加。同时，历年野生动物危害经矩形或圆形校正所得最近邻系数均低于未经校正者，即校正后的聚集程度更高。

2. Ripley's L 统计量

利用CrimeStat 模块中的Ripley's L 分析功能对密云区2011- 2016 年野生动物危害进行分析，其中蒙特卡洛模拟次数为100 次，结果如图1 所示。

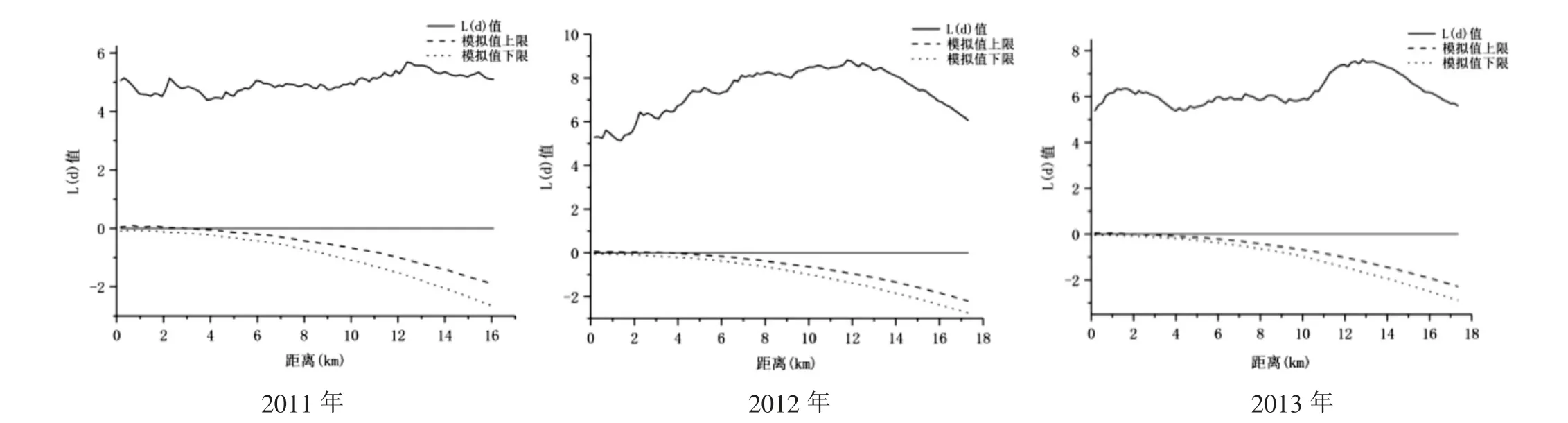
图1 密云区野生动物危害L 函数

由上述结果可见，2011- 2016 年密云野生动物危害Ripley's L 函数表现出了不同的空间聚集模式及聚集强度，但其函数曲线均位于模拟值上限及随机分布之上，即呈现为空间聚集趋势。进一步分析Ripley's L 函数结果可以发现各年份野生动物危害Ripley's L 函数在9- 14km 处达到危害聚集峰值，峰值在6000- 9000 之间，其中2012 年、2014 年及2015 年峰值较高，野生动物危害Ripley's L 在达到峰值之后，虽然仍为正值但随着距离的增加而逐渐下降，即空间聚集趋势不断减弱。

3. 核密度估计

核密度估计可以在地图上将野生动物危害热点连续而直观地表示出来。鉴于可能存在的边缘效应，以高斯正态函数作为核函数为宜。在影响核函数平滑程度的带宽选择方面，据已有研究及多次测试，将带宽设定为1km。核密度估计结果如图2所示。

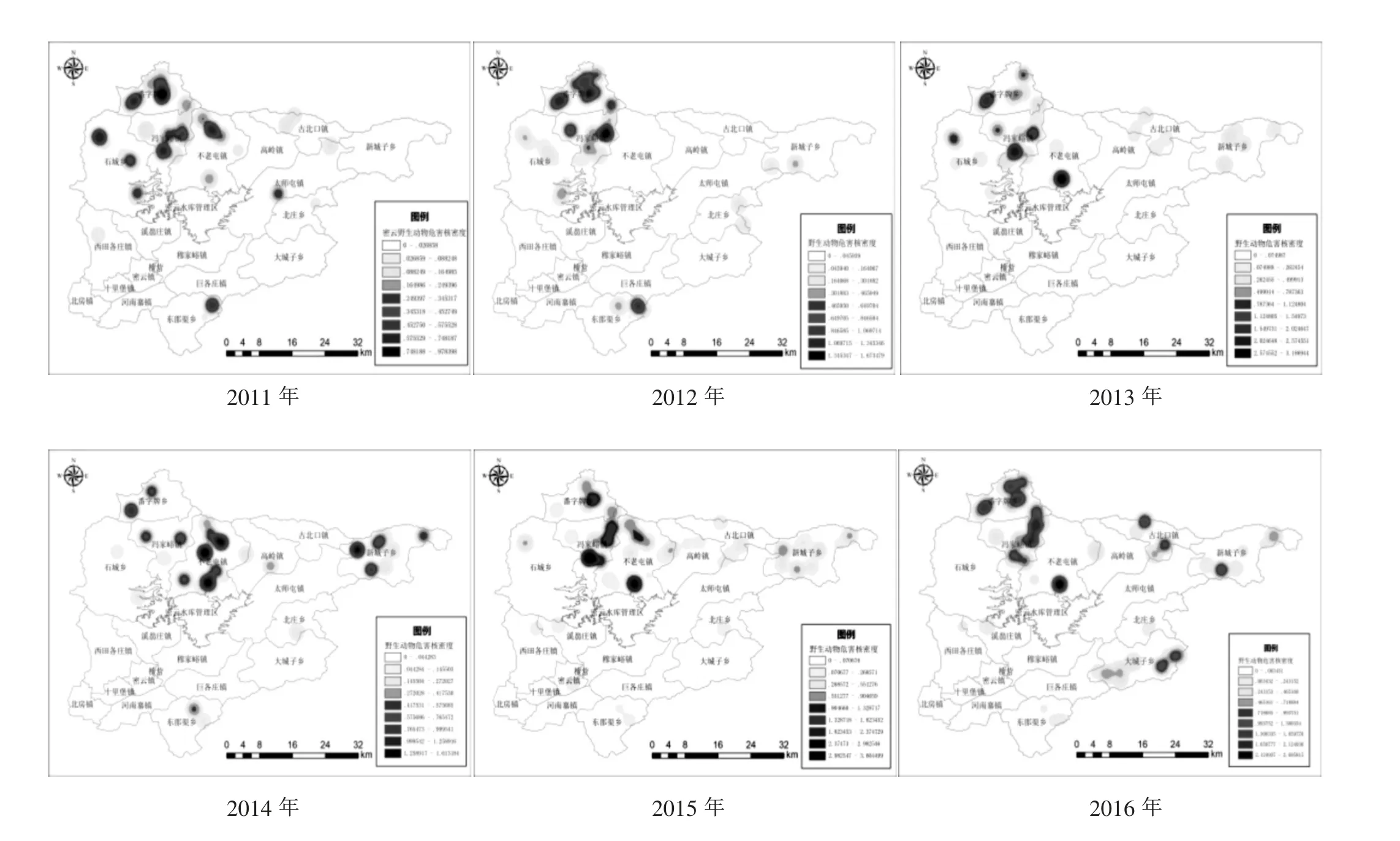
图2 密云区野生动物危害核密度估计

根据核密度估计结果，密云野生动物危害热点分析有以下几个特点：（1）2011- 2016 年密云野生动物危害热点地图均表现出明显的空间聚集趋势。将密云野生动物危害核密度估计值按自然间断点划分为9 个级别后，地图上核密度高值区域与低值区域区分明显。（2）从空间分布上看，密云野生动物危害数量随不同年份而变化但其大致布范围较为固定。番字牌乡、冯家峪镇、不老屯镇、高岭镇、古北口镇、新城子乡、大城子乡和东邵渠乡等密云区多个乡镇在调查年份内均有较多数量的野生动物危害事件发生，其他乡镇则基本不存在野生动物危害事件，这可能与乡镇所处的地理环境有关，密云大多数野生动物危害发生在深山区或半山区乡镇，距离野生动物活动范围更近。（3）密云野生动物危害热点核心区域存在时间上的变化。2011- 2016年密云野生动物危害热点分析结果表明各年份均存在核密度值显著高于周边区域的热点核心区域存在，热点核心区域主要位于石城乡、番字牌乡、冯家峪镇和不老屯镇，不同的是近几年密云野生动物危害的热点核心区域呈由西向东移动的趋势，这可能与野生动物活动范围的变化有关。

五、结论与展望

本文通过空间点模式分析方法，对密云区野生动物危害事件空间点集进行分析，揭示了密云野生动物危害点的空间分布规律。本文主要研究结果如下：

1.密云区野生动物危害最近邻指数的计算，发现密云野生动物危害呈聚集分布，且经过矩形及圆形校正的效果更好，自2013 年以来密云野生动物危害的聚集程度在不断增加。

2.通过对密云区野生动物危害的Ripley's L 统计量分析，可知野生动物危害在各研究距离尺度下具有明显的空间聚集特征。由于野生动物生活习性，野生动物危害表现出明显的空间尺度依赖，在8- 14km 处达到峰值后，其聚集程度普遍随距离的增加而下降。

3.密云区野生动物危害事件的热点分析。核密度分析结果表明，2011- 2016 年野生动物危害事件在密云区内的分布范围及热点区域变化不大，热点聚集区域主要位于于番字牌乡、冯家峪镇、不老屯镇和石城乡，并表现出由西向东发展的趋势。针对野生动物危害空间不均匀分布的状况，可采取差异化治理，同时要关注野生动物危害热点聚集区域的发展方向，及时采取预防措施。

本文注重探究特定研究区域内野生动物危害事件的空间分布特征，可以为野生动物管理部门的政策制定提供参考依据，同时为研究野生动物空间分布提供了新的思路。利用空间点模式分析方法分析野生动物危害仍处于探索阶段，野生动物危害事件的发生往往与野生动物生境和人口密度等因素密切相关。因此，在野生动物危害空间分布规律研究的基础上，还有待结合野生动物危害影响因素，从时间和空间等多个层面进行更为深入的探究。