基于余弦相识度的聚类算法在统计调查对象分类中的应用研究

2019-06-14王习涛马雁疆刘新新

市场研究 2019年5期

王习涛马雁疆刘新新/ 文

长期以来，统计人员使用中位数、众位数、奇异值、比重等统计方法来甄别调查对象报送的统计数据，以期发现其中的错误，进一步提高统计数据质量。本文尝试跳出价值量指标判断的藩篱，采用图形识别的方法对调查对象进行分类，以期发现企业填报的规律，筛选出偏离普遍模式的调查对象。

一、总体设想

现实生活中，我们在首次看到外貌相似的父子、兄弟时，第一印象往往觉得彼此很像，而伴随着相互熟悉之后我们会发现彼此的不同，并且不会再觉得相像，这是我们在识别对象时逐步从面到点的过程。人有各自的相貌，企业统计数据有没有普遍规律呢，能否利用这种规律发现调查对象中的特例，逐步发现我们关心的现象？

企业统计数据由生产过程产生，同一时期、同一地区的企业受基础设施、原材料价格、人员素质甚至风俗习惯、气候的影响，可能会有合理的生产效益关系，本文就从挖掘这种合理通用关系入手，实现对调查对象的分类研究。

假设同一地区，同一时间段，不同规模的企业生产效率是基本相同的，那么映射到二维图上则同序列指标的连线图形应高度相似，如图1 所示，B 企业是A 企业所有指标量值的1/2，则A 企业与B 企业的图形应完全相似。

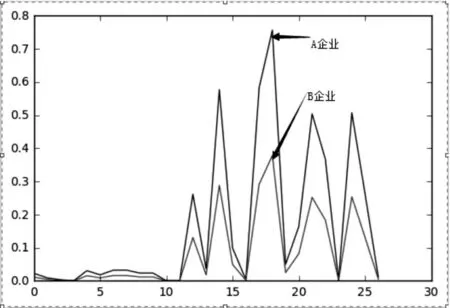
图1 完全相似的两家企业

我们对上图对应数据计算余弦相似度，最终得到两列数据的相似度为1.0000000000000002，由此可以认为这两列数据组成的图形是完全相似的，我们的目的就是找到一个本地区所有企业都高度相似的图形，然后围绕与标准图形的相似度对调查单位分类，通过层层的筛选逐步找到我们关心的调查对象。

二、实验过程

为验证图形模式分类调查对象的可行性，我们采用工业月报B203 表（2- 7 月份）中26 各指标作为测试对象，对数据进行删除零值列预处理、归一化预处理、相似度计算、调查单位聚类，从而将调查单位按照相似度进行分类，并筛选出小众单位。

（一）数据预处理

首先我们观察不同月份的数据，可以发现有部分列数据为零的比重较高，这些列填零的调查对象有两万家左右。两家调查单位填零导致的相似度是没有意义的，这种情况下零较多的列计算出来的相似度是没有参考意义的，因此，首先我们删除填零较多（两万家左右）的列（共删除六列）。

此外，我们的统计指标包含不同量级的价值量指标，如图2所示，由于价值量指标原始数值变动幅度过大，造成图形中大多数指标趋近于零，从而导致仅有价值量值较大的指标才会影响相关度。

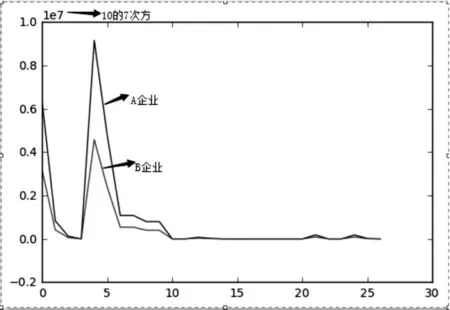
图2 原始数据图形

为消除不同量级指标对相关性的影响，我们对原始数据进行规范化处理，常用的规范化处理方法有最小最大规范化、零均值规范化、数量级归一化、极差归一化［（0,1）标准化］、Sigmoid 函数归一化、softmax 函数归一化等，我们采用极差归一化［（0，1）标准化］对原始数据去量纲处理。

极差归一化是最简单、最容易想到的数据归一化方法，它将变量的极差线性变化到（0,1）区间，假设属性x 的最大、最小值分别为max（x）和min（x），则每一个具体的值x 按如下公式规范化得y：

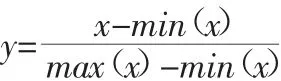
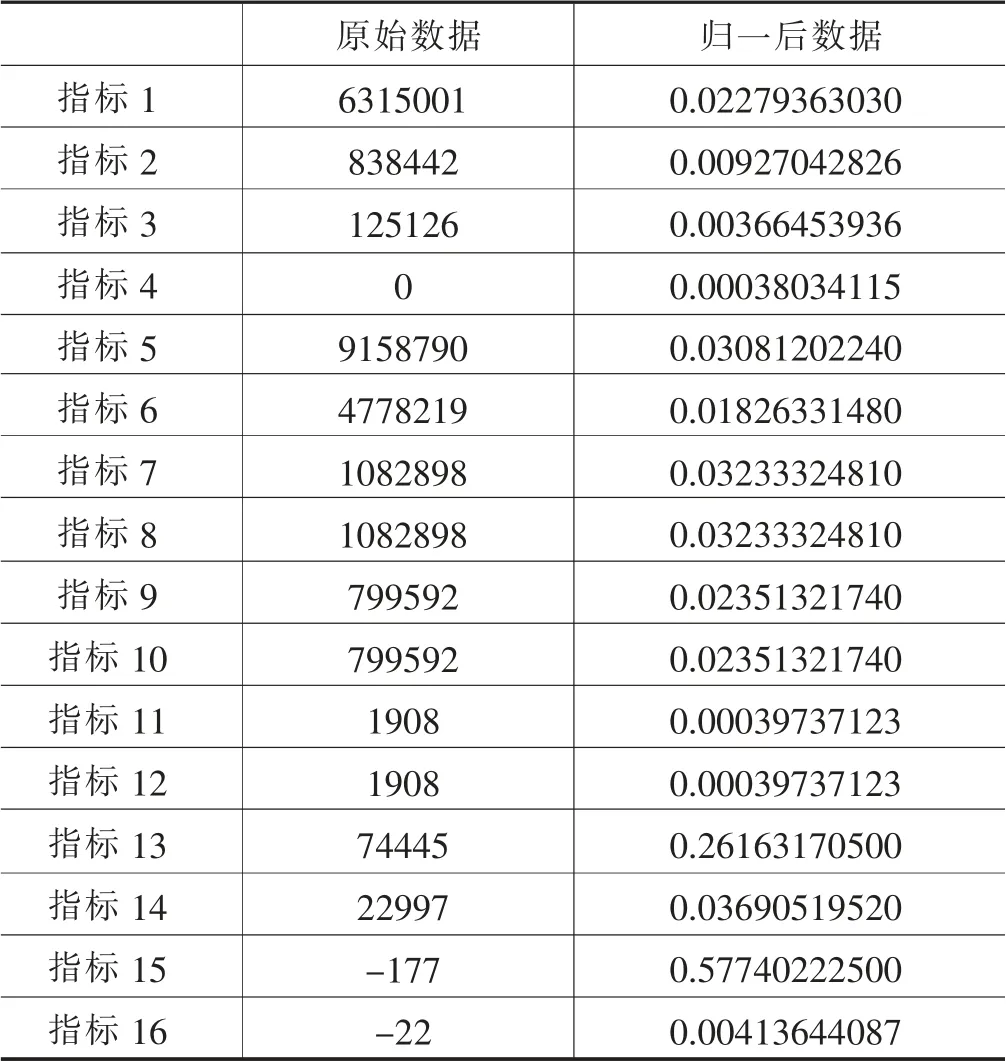
表1 原始数据及归一后效果

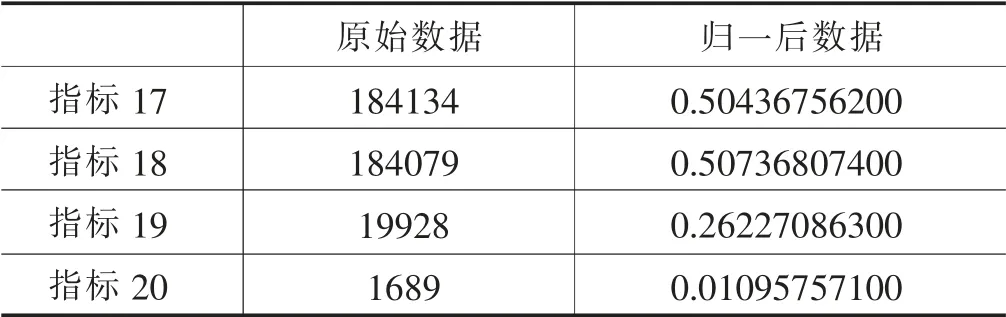
续表

（二）相关度计算

通过预处理后的数据被存放在22000 多行（每月单位数不完全一样），20 列的矩阵中，每一行代表一个调查对象，我们需要对任意两行计算其余弦相似度，从而判断两个调查对象报送的报表是否相似。

余弦相似度通常用在文档相似度判断上，是利用两个向量夹角的余弦值来衡量两个向量差异的大小，余弦值越接近1，就表明夹角越接近0°，也就是两个向量越相似，余弦相似度不考虑两个数据对象的量值。

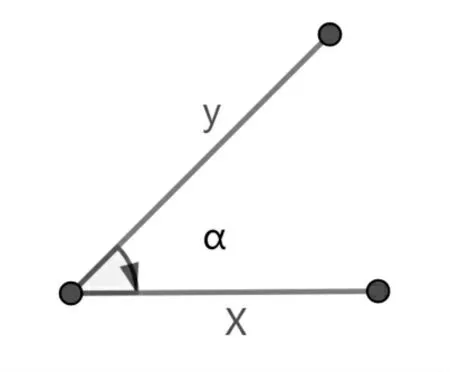
图3 余弦相似度的几何解释

如图3 所示，边x 与y 的余弦相似度是边x 与y 之间的夹角α 的余弦值。因此，如果余弦相似度为1，则x 与y 之间的夹角为0°，此时除了长度外x 与y 是相同的，如果余弦相似度为0，则x 与y 的夹角为90°，x 与y 完全不相似。

在二维空间，根据向量点积公式，显然：

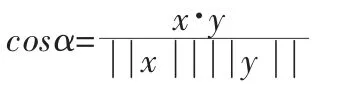
假设向量x、y 的坐标分别为（x1,y1）、（x2,y2）。则：

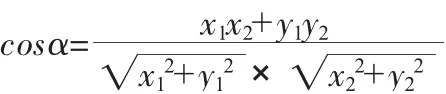
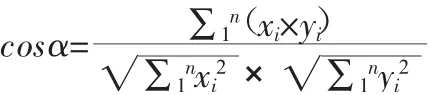
注：

算法：对任意两行数据（m 行、n 行）执行下面程序：

CompCosα（m，n，cosa）

1.当i 小于指标数时继续执行，否则跳到第5 步（i 从0 开始记录已计算指标数）

3.计算m 行对应i 指标的平方（xi2），并累加。

4.计算n 行对应i 指标的平方（yi2），并累加。

5.对2、3、4 步累加结果计算cosα。

6.返回cosα。

（三）按照相似度进行聚类分析

常用的数据分类分析方法有很多，如贝叶斯分类、支持向量机分类、神经网络分类等，而多数分类需要先确定分类条件或训练样本。聚类分析是根据“物以类聚”的道理对数据进行分类，分类前无须确定分类条件，是一种无监督的分类过程，非常适合统计调查对象分类。

正确合理的理解数据分析需求是选择聚类方法的基础，在面部识别程序中，无论对象什么样貌、什么肤色，或者外部器官发生病变甚至缺失，只要对象是人，程序都应该做出人脸的判断，统计调查对象识别也一样，无论是大企业还是小企业，甚至企业部分数据缺失，程序都应该能判断出这是企业填报的数据，除非数据是非专业人员人为臆造的。在这种情况下，我们的调查单位应有一个通用的标准，而这个标准在多维数据空间中应该映射到一个具体的点（我们称之为中心点），而各个调查企业与这个点的距离（相似度）就是判断企业数据真伪的标准。

在现实中我们依然很难计算出中心点的具体位置，因为我们使用的是图形模式相似度距离，而不是绝度量距离。在这种情况下我们可以变通一下，首先我们设想一下调查对象在多维空间中的可能分布情况，第一种情况是多数单位聚集在一个簇中，少数指标游离于簇外。第二种是形成多个簇。不管是哪种情况，每个簇必然至少有一个离中心点距离最近的调查对象点，而以这个点为中心将囊括该簇最多的调查对象，这样寻找中心点的问题转化为寻找包含样本最多的问题，这也呼应了聚类分析的优势，因此我们使用K 中心点聚类算法，首先设定K 等于1，验证第一种设想。

注：

算法：发现包含等距离（相似度）调查对象最多的点

FindCore（m，datamatrix）

1.当i 小于调查对象数时继续执行，否则跳到5 执行。

2.当j 小于调查对象数时继续执行。

3.计算i 与datamatrix（归一化后数据矩阵）每一行（j）的相似度，记录相似度低于设定值的行。

4.判断与i 相似度低于设定值的调查对象数是否创新低，如果创新低则存储，否则i 加一跳到1 行继续执行。

5.输出所有记录的中心点及对应的低相似度调查对象集合。

（四）实验结果

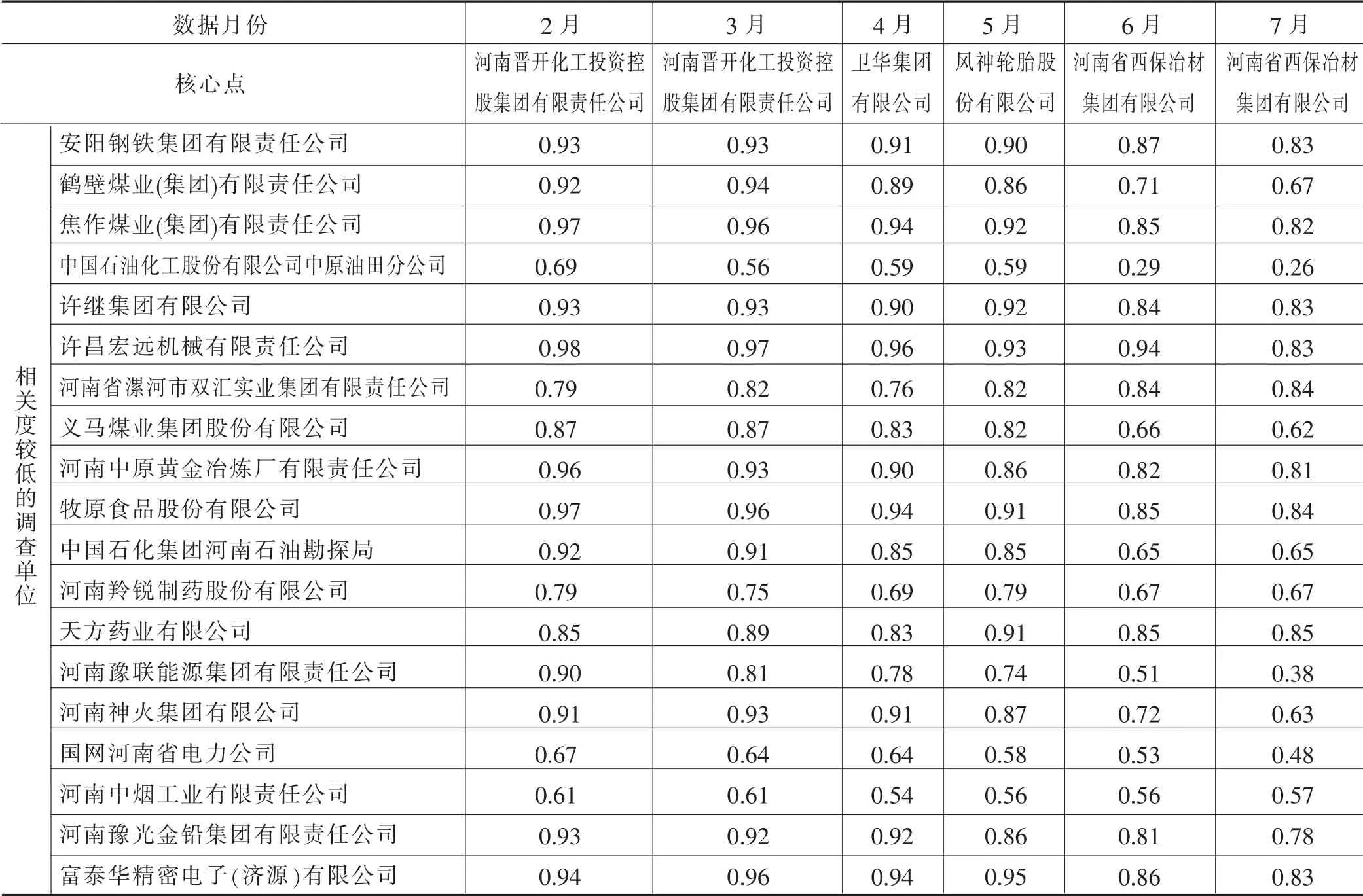
以联网直报平台查询导出默认顺序对数据进行扫描，以每个调查对象为中心点执行聚类，并记录每一次扩大聚类范围时的中心点及聚类单位数，表2 记录了2 月份B203 表每次扩大聚类范围时的中心点及相关度较低的调查对象。以最后第一个出现的最大聚类集为最优聚类集，表3 记录了对2 至7 月份数据进行聚类后的中心点及相似度低于0.9 的调查单位。

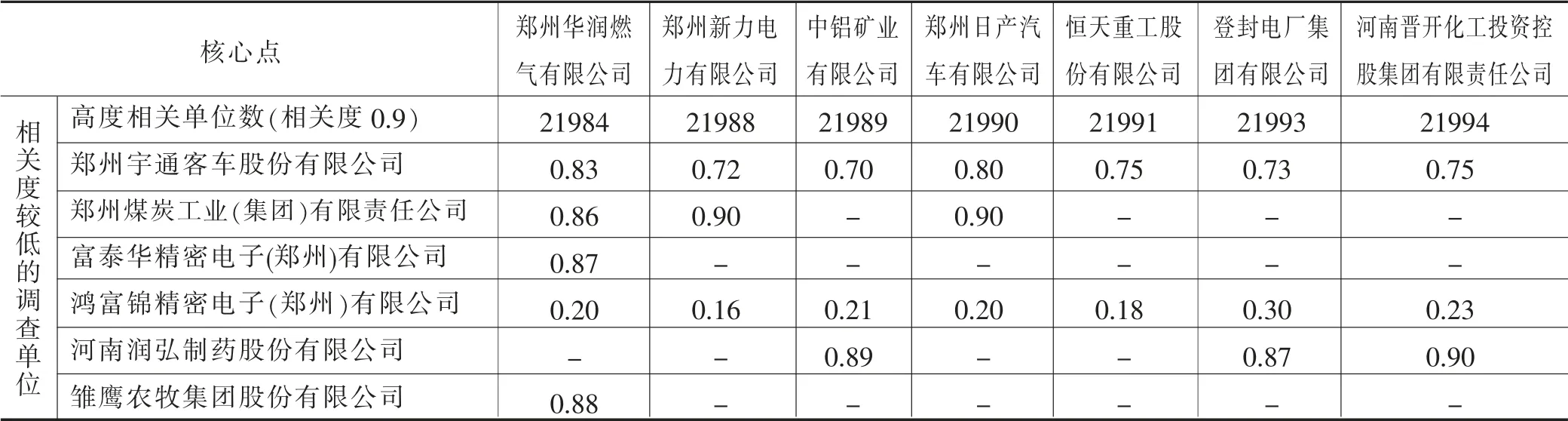
表2 2 月份B203 表调查单位聚类结果（空白区相关度大于0.9）

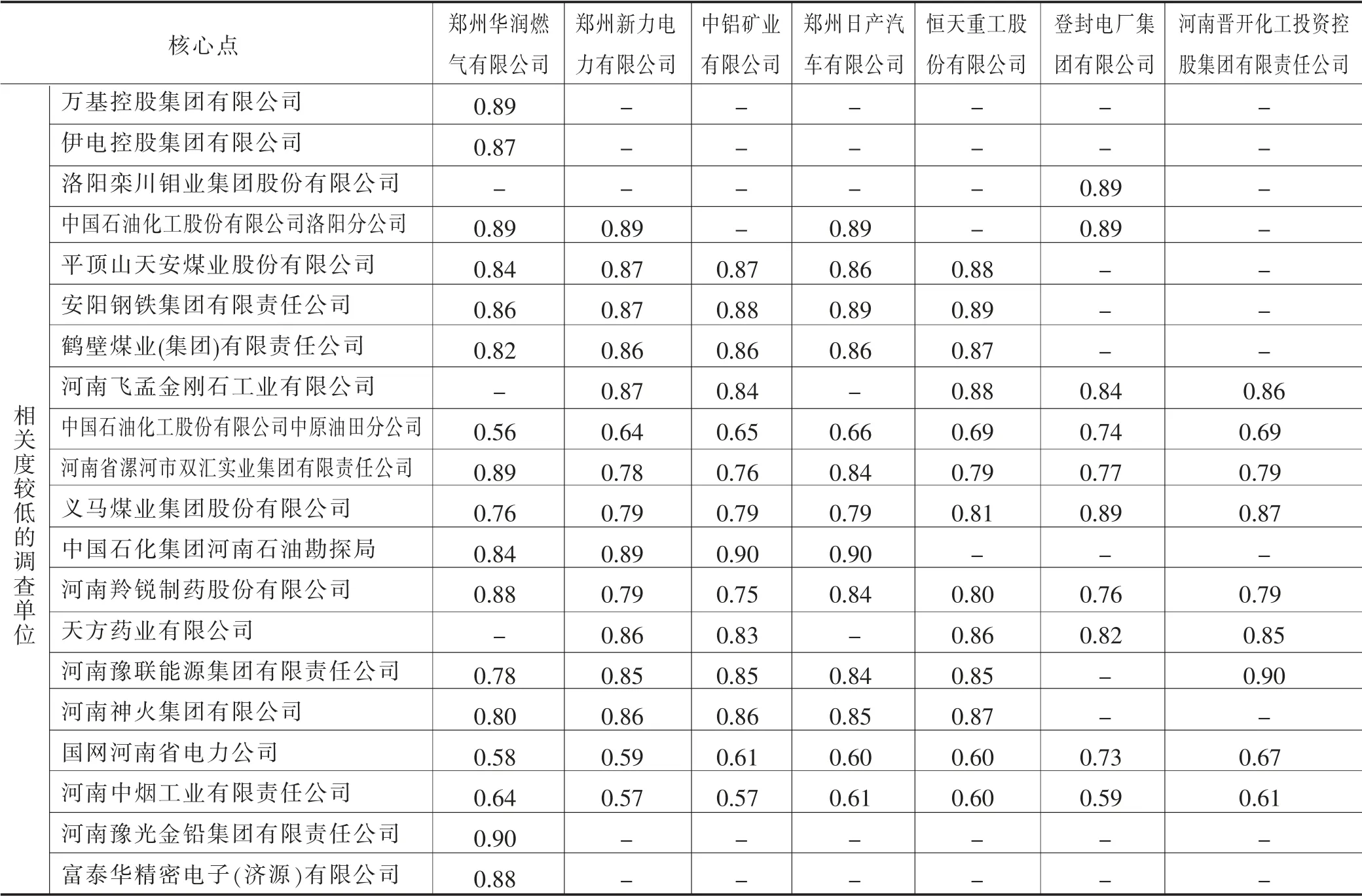
续表

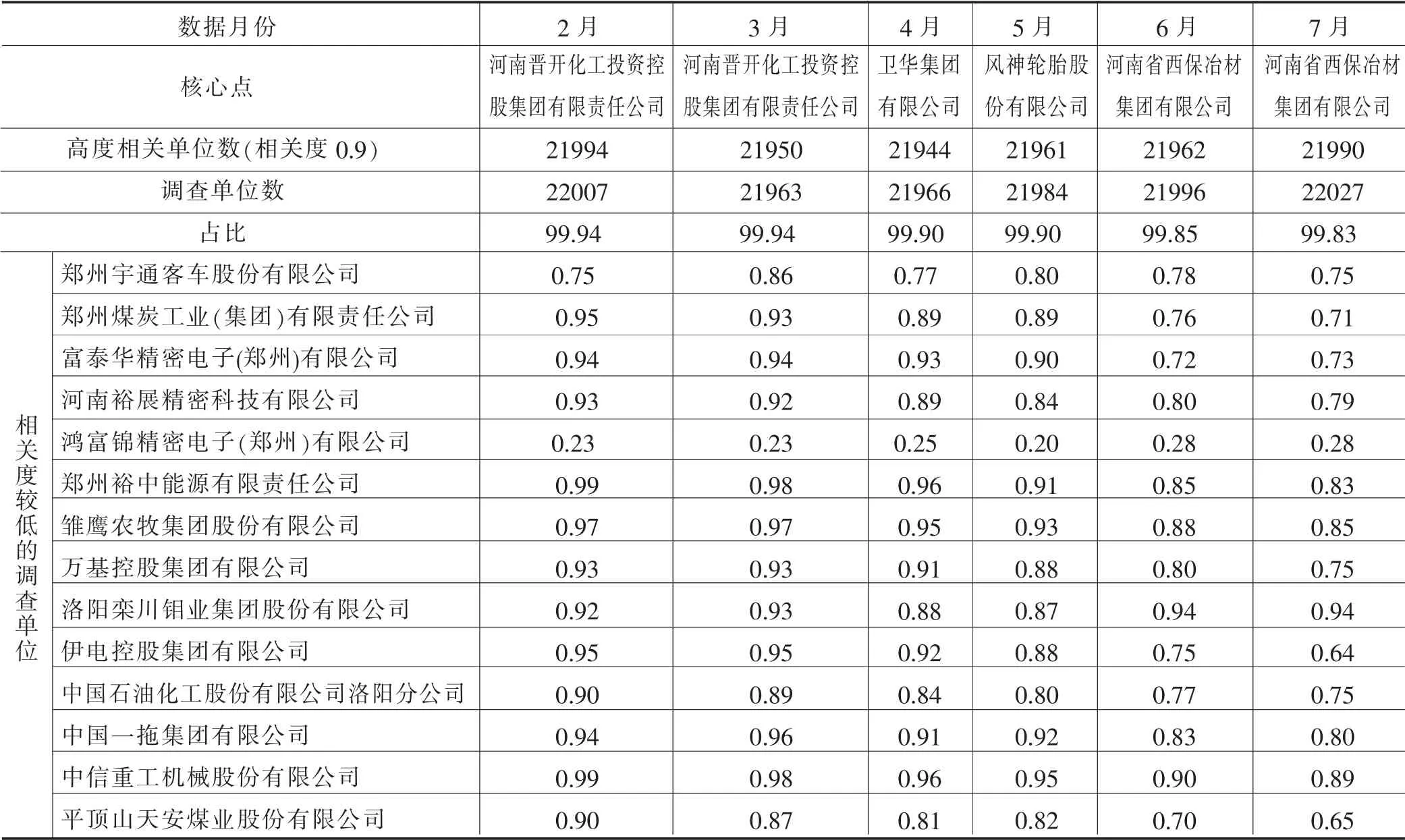
表3 2-7 月B203 表数据分析结果

续表

三、结果分析

从表3 可看出，填写B203 表的调查单位聚集度较高，99.9%的调查单位聚集在不低于0.9 相似度的集群中，这说明我们选用的样本数据整体上是稳定的，没有受到个别离群单位影响，这符合第一种设想，也证明在初步分类中全省B203 表填报质量较高。

逐月观察可以发现，2 至7 月份与核心点相似度低于0.9的调查单位在逐步增多，相似度持续低于0.9 的企业中宇通客车、鸿富锦电子、双汇实业、天方药业和中烟工业始终保持与不同核心点的近似相似程度，企业数据与核心点相似度较低应该是企业特殊经营管理造成的（见图4）。

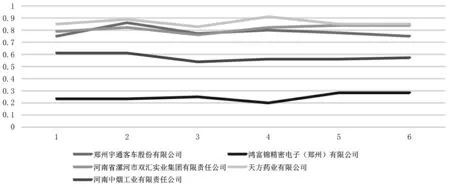
图4 持续低于0.9 并保持稳定的企业

中石化中原油田、义马煤业、羚锐制药和省电力公司，从2月份开始与不同核心点相似度就小于0.9，并呈持续下降态势，说明企业填报数据与核心点的差距在逐步拉大（见图5）。

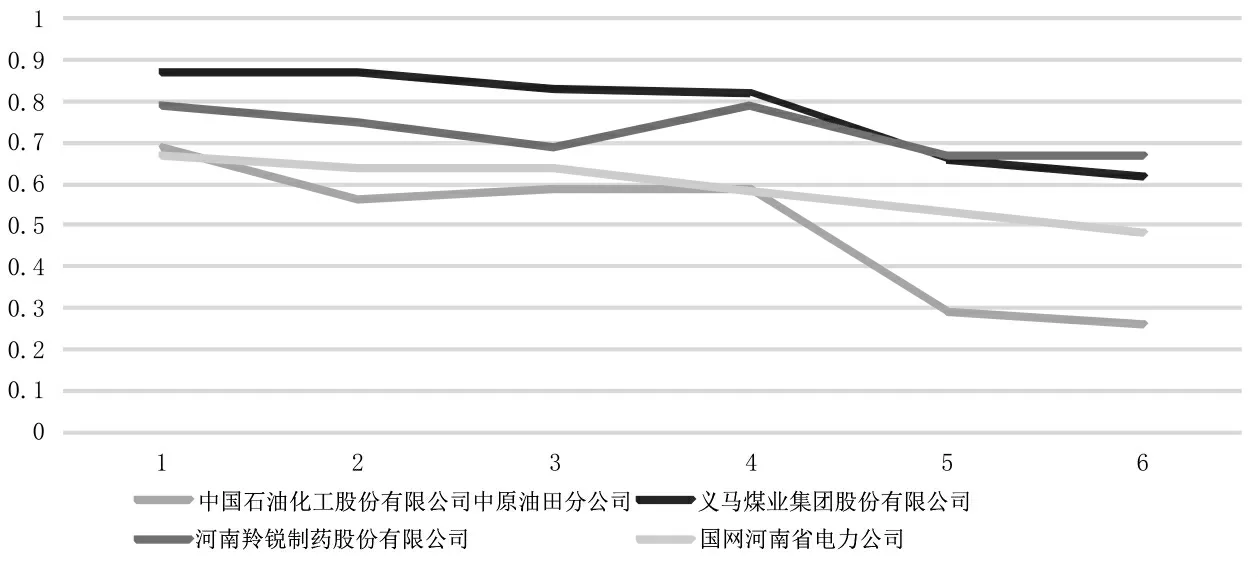
图5 相似度低于0.9 并逐步下降的企业

表3 中其他企业如郑煤、富泰华电子、焦煤和中石化河南勘探局从最初与核心点高于0.9 相似度逐步下滑至低于0.9 相似度，体现了企业填报模式由高度接近核心点逐步偏离核心点（见图6）。

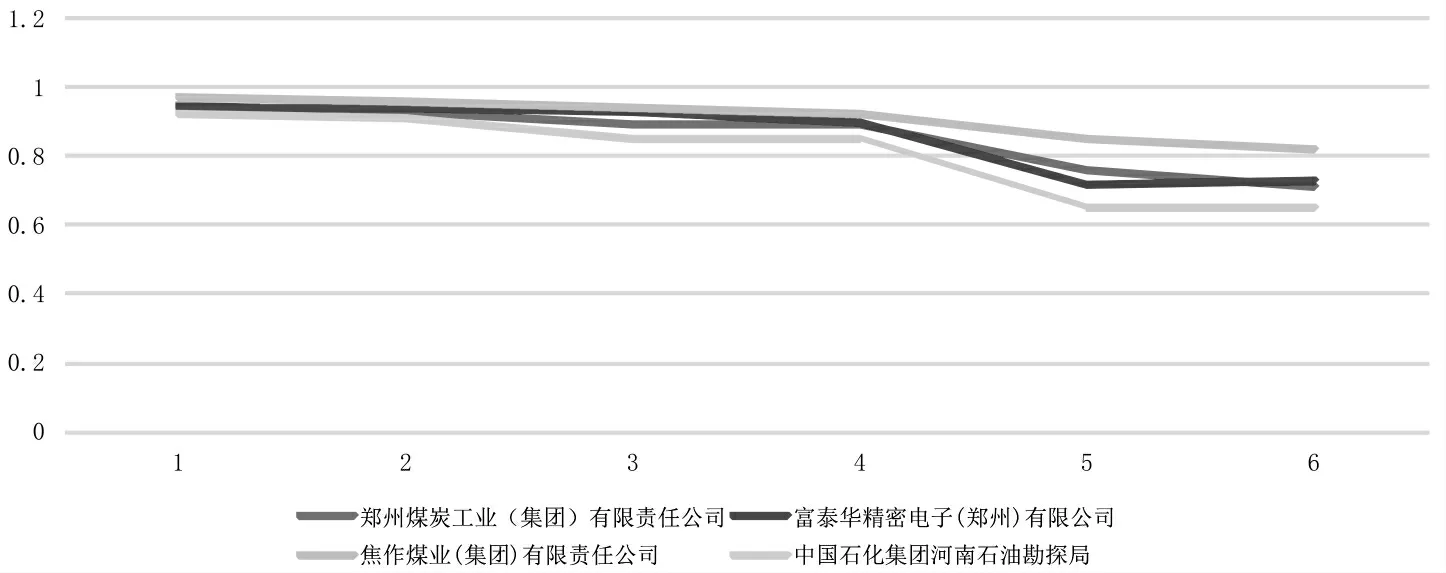
图6 相似度高于0.9 下滑至低于0.9 的企业

而大多数调查单位始终保持高于0.9 的相似度，反映了大多数企业始终坚持稳定合理的填报模式，确保统计数据整体稳定。

四、改进方向

余弦相似度通常用在文档相似性度量领域，本文创新性地将余弦相似度用在企业填报数据的图形识别上，试图探索出一条抛开价值量含义，实现整体识别判断的新道路。通过实现，发现图形识别确实能够发现企业填报模式的区别，但灵敏度需要进一步改进。

（一）加强数据预处理

虽然前期我们对数据删除了零值较多的列，进行了极差归一化处理，但数据预处理工作仍有改进的空间。由于调查对象属性指标较多，需要进一步判断是否需要进行主成分分析，筛选更具代表性的属性，剔除干扰属性，提高识别准确率。此外极差归一化只是将价值量指标的值域直接映射到[0,1]范围内，但是指标分布密度没有本质改变，能否增加一个散列函数，将指标均匀分部到[0,1]之间，从而合理扩大均匀散布调查对象的值差距。对指标中的相同数字处理也是需要进一步考虑的问题，不等于零的重复价值量是有意义的，而相同的零值被判断为高度相似就应该设法筛除掉。