基于ARIMA和BP神经网络对人民币汇率预测的比较分析——以美元人民币汇率为例

朱家明，胡玲燕

(安徽财经大学 a.统计与应用数学学院; b.金融学院, 安徽 蚌埠 233000)

2005年，我国进行了汇率改革，宣布采用浮动汇率制度，参考一篮子货币进行调节，这使我国汇率受到市场供求关系的影响，波动范围进一步扩大，人民币出现较大幅度升值[1]。2015年，我国又开展了新一轮汇率改革，宣布当日人民币中间价需要参考上个工作日人民币的收盘汇率和一篮子货币汇率的变化[2]，这意味着我国汇率制度不断完善，且不断向汇率市场化发展。而汇率的波动对个人投资、企业进出口、国家国际收支等来说都有密切关系，因此对汇率走势进行预测具有重要意义[3]。

国内外学者对汇率预测也进行了相关研究。在国外，Refenes等利用神经网络和平滑法进行汇率预测，发现神经网络预测效果更优[4]。而Svitlana则发现神经网络更适用于对汇率进行短期预测[5]。国内戴晓枫等发现EGARCH对人民币汇率的预测效果优于ARIMA模型[6]。刘潭秋利用线性和非线性时间序列研究发现LSTAR-GARCH对人民币汇率的拟合效果更好[7]。而本文分别利用ARIMA和BP神经网络模型，根据中国货币网2017年12月1日至2018年10月8日(除节假日外)的美元兑人民币汇率数据，对2018年10月9日至10月29日(除节假日外)的15天汇率进行预测，进而判断模型预测效果，为企业根据汇率走势把握进出口汇兑风险，个人减低投资风险等提供借鉴。

1 基于ARIMA模型对人民币汇率的预测效果分析

1.1 研究方法及思路

自回归移动平均模型(ARIMA)由美国统计学家Box和Jenkins于20世纪70年代提出[7]。ARIMA被广泛用于时间序列预测分析，其实质是利用差分运算将非平稳时间序列转化为平稳时间序列，再建立ARIMA模型并进行预测分析。在模型ARIMA(p,d,q)中，p为自回归阶数，d为数据差分次数，q为移动平均阶数。模型的基本结构为：

其中，Θ(B)是移动平滑系数多项式，而φ(B)是自回归系数多项式， {εt}是零均值白噪声序列[8]。而本文利用ARIMA模型对2018年10月9日至2018年10月29日(除节假日外)的人民币汇率数据进行预测，并利用2017年12月1日至2018年10月8日(除节假日外)的人民币汇率数值作为实验数据，数据均来源于中国货币网。首先采用时序图和ADF检验对数据的平稳性进行判断，若不平稳则作差分再次检验，若差分平稳，则对差分序列进行自相关和偏自相关检验，初步判断ARIMA的自回归阶数和移动平均阶数，并结合AIC、SC、HQ准则对ARIMA进行识别和定阶，选择最优 ARIMA模型并利用其残差序列和相关系数对模型效果进行判断，最后预测数据，并分析预测效果。

1.2 预测分析过程及结论

1) 平稳性检验和处理

时间序列建模要求数据平稳，因此首先对原数据的平稳性进行判断，本文选择时序图和较常用的ADF检验进行判断。利用EVIEWS 10绘制出样本的时序图，见图1。由图1可以看出：数据波动较大，且呈现先下降再上升的总体趋势，初步判断数据不平稳，再对其进行ADF检验。在ADF检验过程中，依次选择含截距项和趋势项、含截距项、原序列3种情况进行逐步的检验和剔除，得到的检验结果如表1所示。可知在5%的显著性水平下，人民币汇率数据存在单位根，数据不平稳，因此对原序列进行一阶差分，见表1。可知一阶差分序列在5%的显著性水平下平稳，因此可以用其进行ARIMA建模，且在ARIMA模型中差分次数为1。

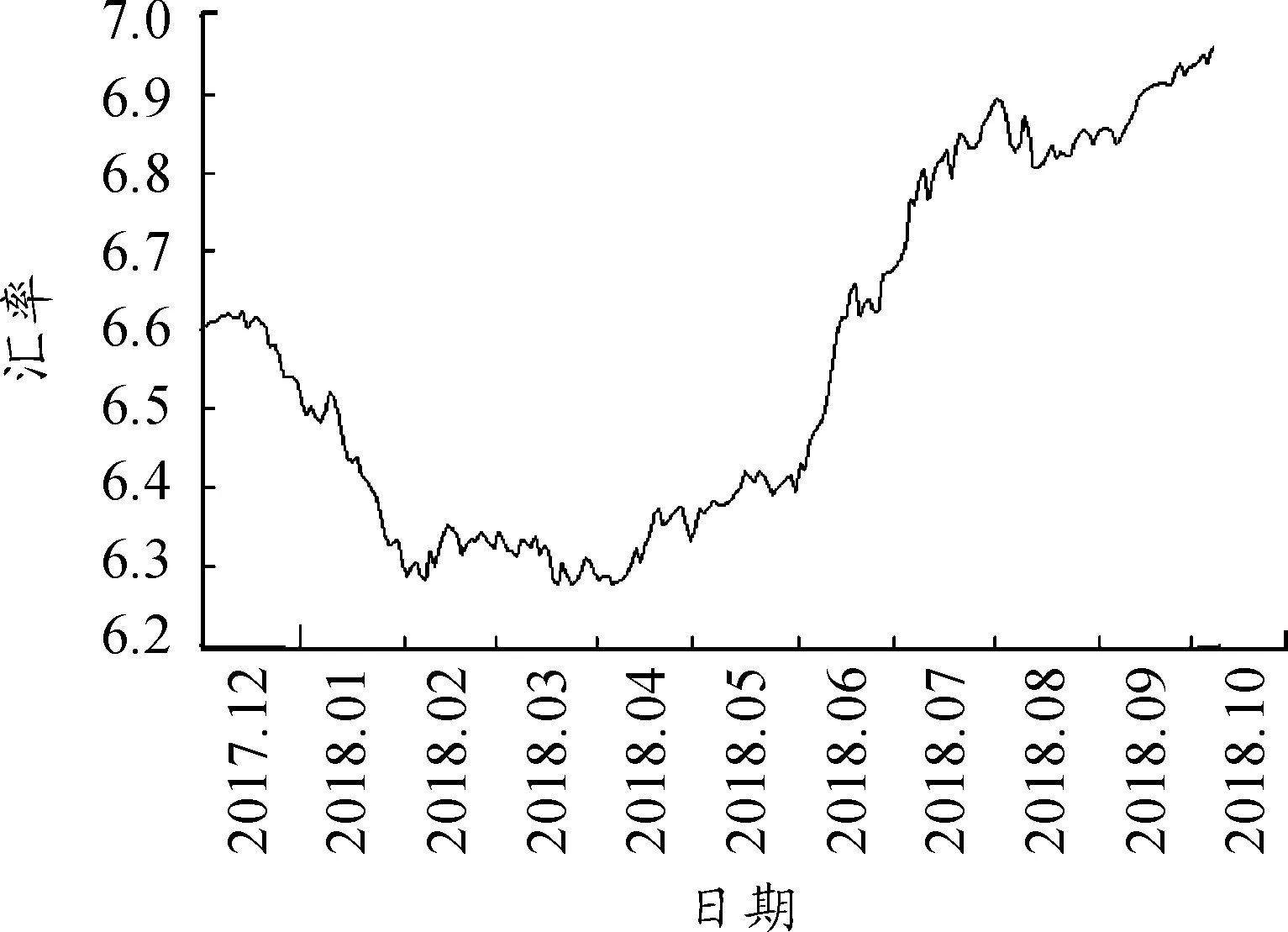
图1 人民币汇率时序图

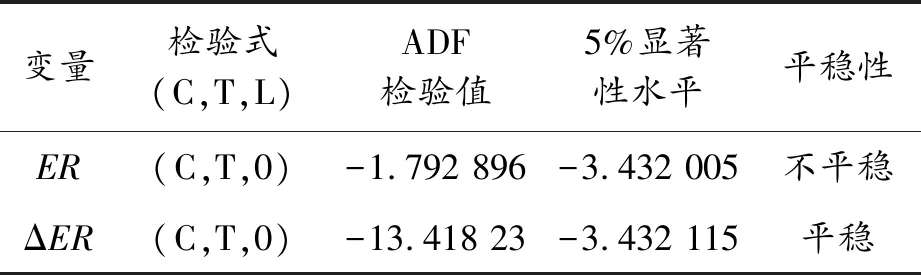
变量检验式(C,T,L)ADF检验值5%显著性水平平稳性ER(C,T,0)-1.792 896-3.432 005不平稳ΔER(C,T,0)-13.418 23-3.432 115平稳

2) ARIMA识别和定阶

已知一阶差分数据为平稳的时间序列，满足ARIMA模型建立的初步要求，但还需对模型进行识别和定阶。目前，广泛应用的ARIMA识别和定阶方法是利用偏自相关系数、自相关系数和AIC、SC、HQ准则进行拟合效果判断，确定最优ARIMA[9]。因此，本文利用SPSS软件得到一阶差分序列的自相关系数和偏自相关系数及其相关图，见图2。可以看出图形中有较为明显的拖尾，并初步判断自相关和偏自相关皆为3阶或4阶拖尾。为了进一步确定模型的自回归阶数及移动平均阶数，分别建立模型ARIMA(3,1,3)、ARIMA(3,1,4)、ARIMA(4,1,3)、ARIMA(4,1,4)，并结合AIC、SC、HQ值综合确定模型参数(如表2)，发现ARIMA(4,1,3)的AIC、SC、HQ值皆为最小，根据最小化原则，选择建立ARIMA(4,1,3)模型。

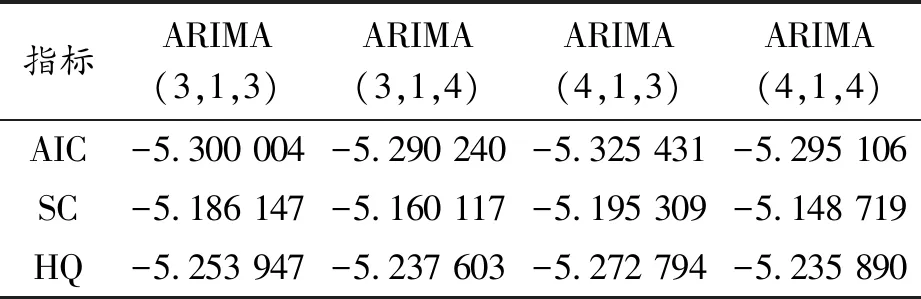
表2 模型精度指标对比

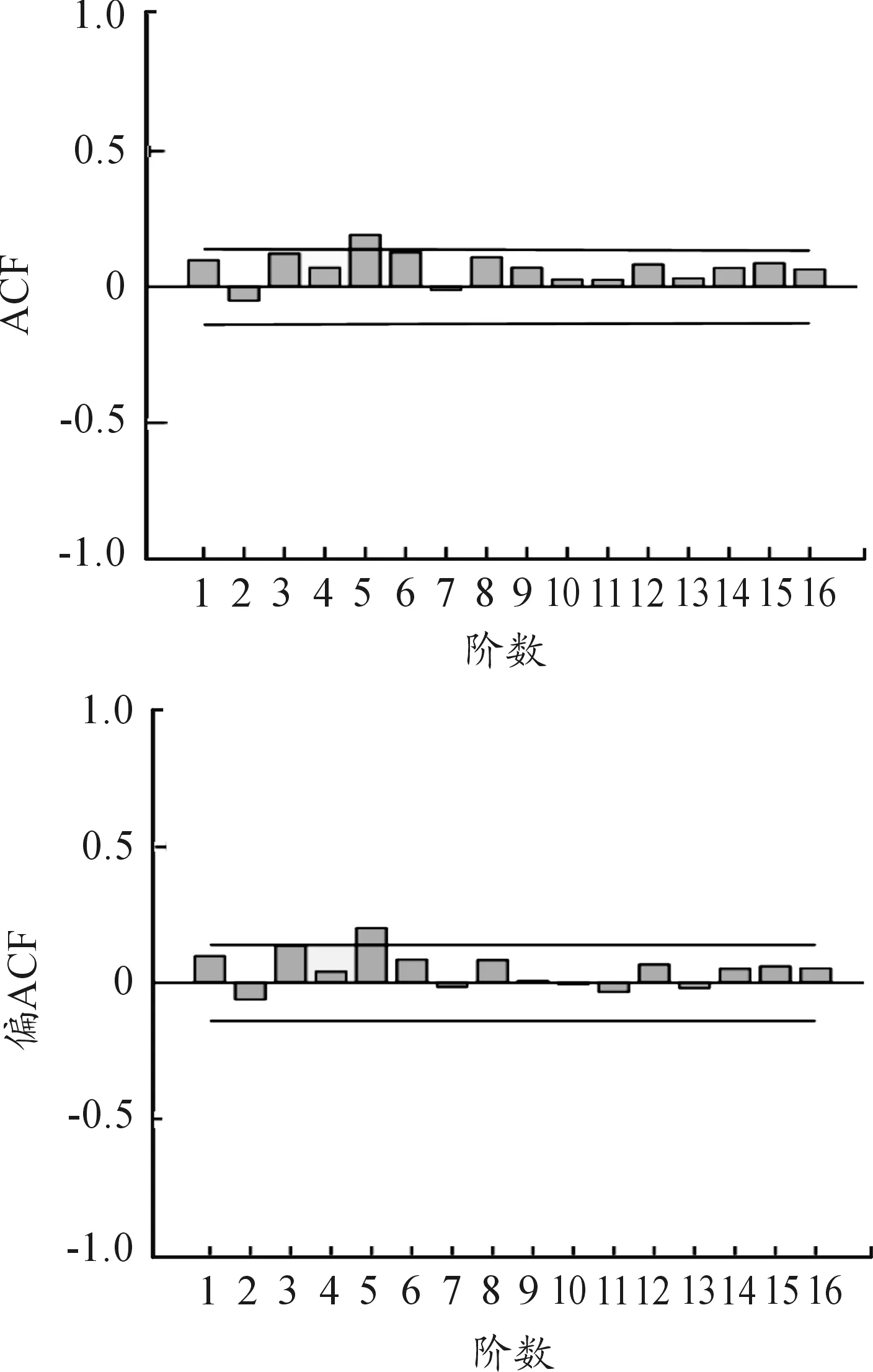
图2 ACF和PACF图

3) 模型的检验及预测

为了判断模型的有效性，还需对ARIMA(4,1,3)模型的残差进行序列和自相关检验，见图3和表3。

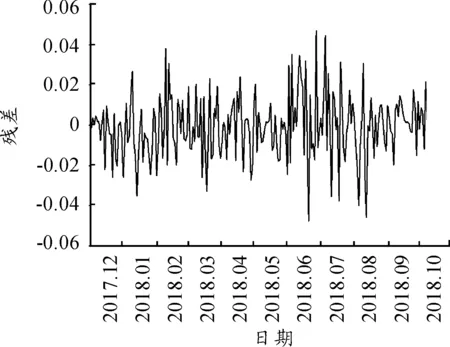
图3 残差序列

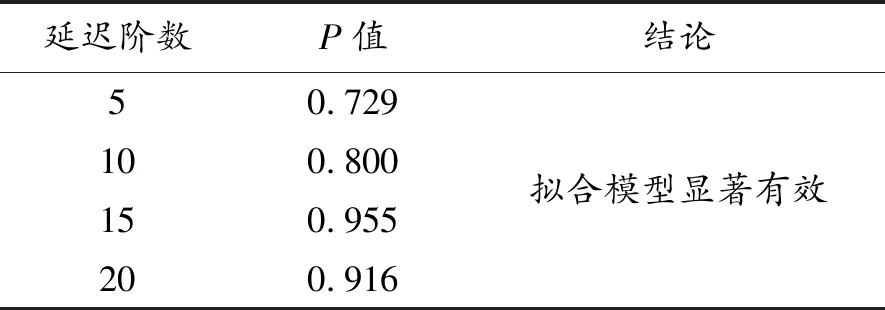
延迟阶数P值结论50.729100.800150.955200.916拟合模型显著有效

由残差序列图和自相关检验结果可知：模型的残差序列较均匀地分布在两侧，其自相关系数P值均远大于0.5，说明残差序列为白噪声序列，模型已提取大部分有规律的重要信息。且该模型预测效果较好，因此模型建立有效可行。利用该模型对2018年10月9日至2018年10月29日15个工作日的人民币汇率进行预测，并与实际汇率数值进行对比，见表4。

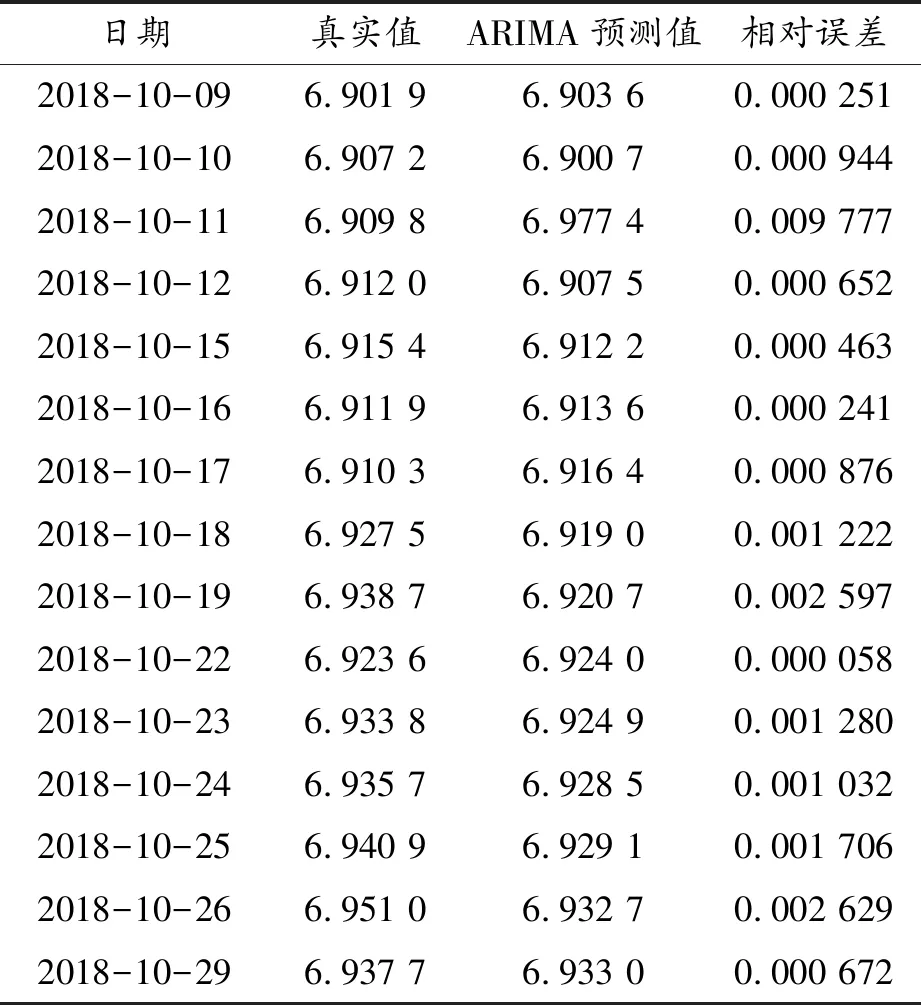
表4 人民币汇率预测结果

由表4可以看出：人民币汇率真实值与预测值的趋向大体一致，且两者的相对误差较小，其中最大相对误差仅为0.009 777，最小相对误差为0.000 058，平均相对误差为0.001 627。说明利用ARIMA模型对人民币汇率进行预测具有一定的可行性，预测整体效果较好，可以有效预测未来汇率的走势。此外，随着预测时间的推移，预测值与实际值的偏差有扩大的趋势，因此该模拟更适合进行短期的汇率预测。

2 基于BP神经网络模型对人民币汇率的预测效果分析

2.1 研究方法及研究思路

人工神经网络是一种通过模仿人类大脑神经传递特征所建立的一种复杂系统，仅依靠数据自身的变化，具有自我鉴别行为模式的能力，因此也被运用于多个领域。而其中BP神经网络是包含一个输入层、一层隐含层、一层输出层的多层前向型神经网络[10]，其结构如图4所示。其工作原理是整个工作过程都是按照有“导师”的方式进行训练，并采用信息向前传递和误差反向传递的算法，根据每一次迭代结果逐次修正各连接权，提高模型响应的正确率，直到达到预设的预测精度要求或预设的迭代次数[11]。

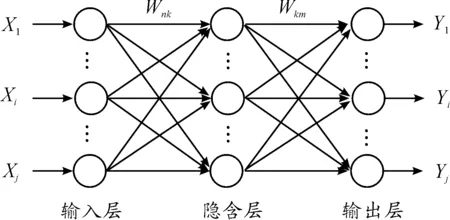
图4 BP神经网络结构

本文将前4日的美元兑人民币汇率作为输入变量，第5日作为输出变量，并将前186组变量矩阵作为训练样本，后15个变量矩阵作为测试样本。根据计算公式和最小均方差原则设定隐含层神经元个数，并确定BP神经网络模型的整体结构为4-4-1。然后设定网络的各训练参数，包括学习算法、训练函数、性能函数和传递函数等[12]。然后利用Matlab软件对模型进行训练，并利用最优训练网络对2018年10月9日至2018年10月29日人民币汇率进行预测，并与真实汇率数据进行比较，进而评价模型的预测效果。

2.2 预测分析过程及结论

1) 模型结构确定及参数设置

首先将2017年12月1日至2018年10月8日的人民币汇率数据进行有效处理，其中将前4天的数据为输入变量，第5天为输出变量，形成一个186行乘以5维的变量矩阵，即模型为4个输入层和1个输出层。然后根据公式进一步确定神经元个数[13-14]：

其中d=4,k=1,b为1～10之间的常数。因此，初步确定模型的神经元个数为3～13个，然后结合模型的最小均方差，采用试凑法进行逐个判断，最后确定隐含层的神经元个数为4。综上设定BP神经网络结构为4-4-1。然后对模型的参数进行设定，其中传递函数为Tansig，训练函数为Trainlm，权重和阈值的学习算法以及性能函数分别为Learngdm，Mse。此外，模型的目标误差为1×10-5，最大迭代次数为1 000次。

2) 模型预测

模型设定完成后，利用模型对数据进行训练和预测，并利用训练好的BP神经网络模型对2018年10月9日至2018年10月29日人民币汇率进行预测，训练结果如图5、6所示。

由图可知，模型的训练数据、验证数据以及测试数据的均方误差在epoch2前迅速减小，并在epoch10时达到最小值0.000 302 67，此时神经网络训练的结果最佳。

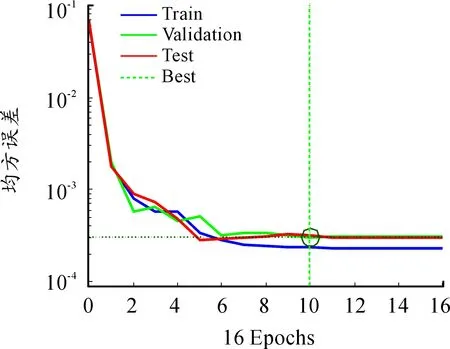
图5 均方误差

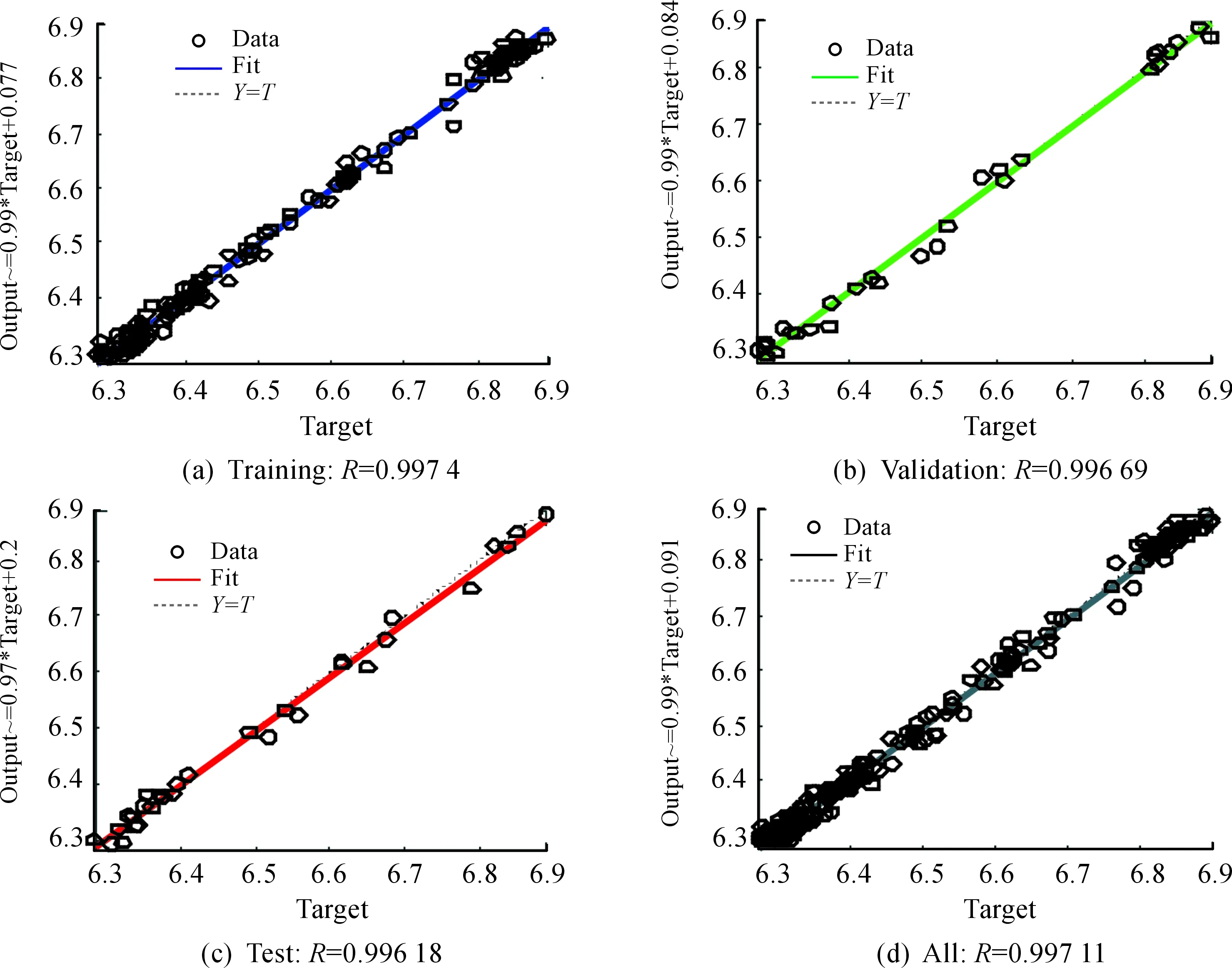
图6 拟合效果图

由图6可知：所训练的BP神经网络对数据拟合效果很好，其中训练数据拟合R值达0.997 4，验证数据、测试数据及所有数据的拟合R值分别为0.996 69、0.996 18、0.997 11，均大于0.99，模拟拟合效果好，可用于预测2018年10月9日至2018年10月29日人民币汇率，得到的预测结果如表5所示。

由表5可以看出：人民币汇率预测结果的整体相对误差较小，其中最大为0.008 03，最小为0.002 68，平均相对误差仅为0.004 632，整体来看BP神经网络预测效果较好，但随着预测时间的推移，相对误差有增大的趋势。因此，BP神经网络模型对人民币汇率进行短期预测更有效。而0.004 632>0.001 627，故与ARIMA模型相比，BP神经网络对人民币汇率的预测效果较差。

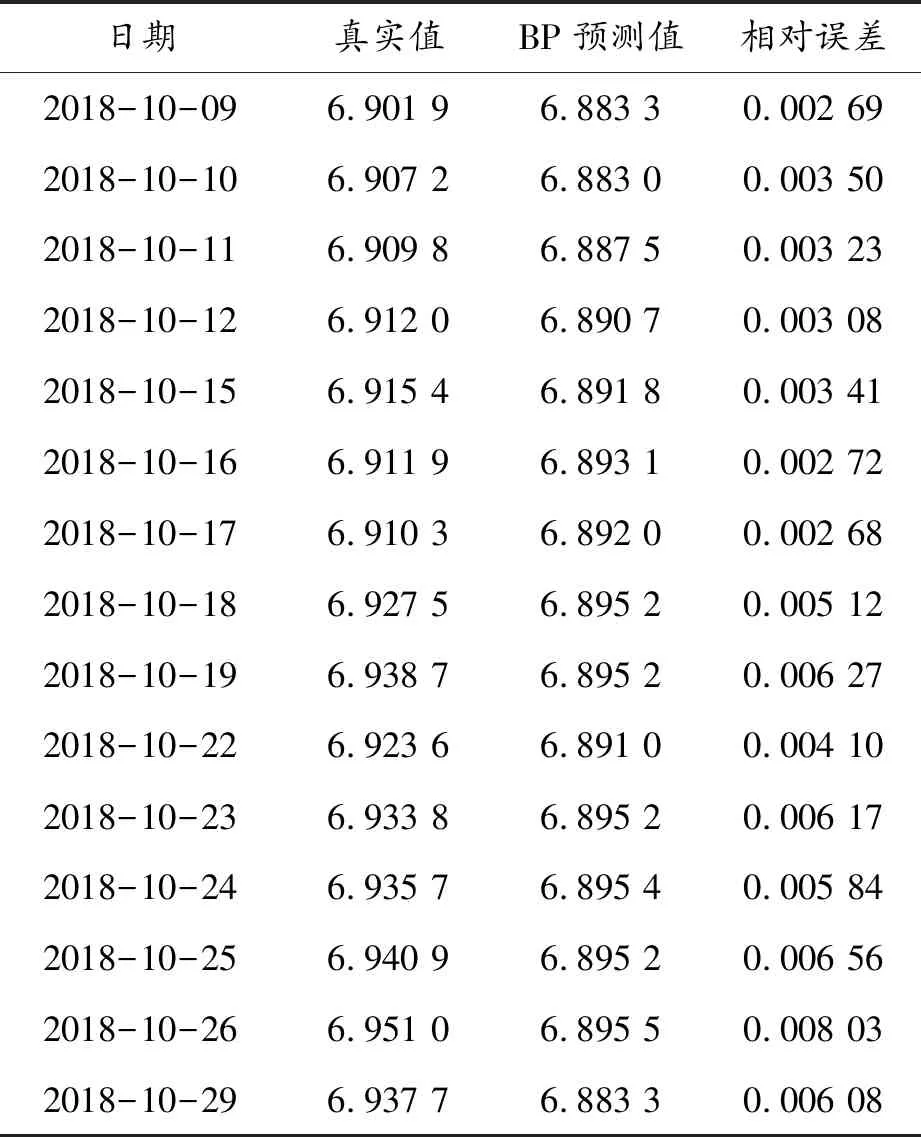
表5 人民币汇率预测结果

3 结论

本文利用ARIMA和BP神经网络模型对美元兑人民币汇率分别进行预测分析发现：

1) 两模型对人民币汇率的预测有效，预测精度较高。

2) 相比之下，ARIMA模型的预测效果优于BP神经网络，相对误差更小。

3) ARIMA和BP神经网络对人民币汇率的预测精度随着预测时间的推移而下降，两模型更适用于短期预测。

但本文也存在不足之处，仅用相对误差判断模型的预测精度，若能结合未来汇率的变动趋势进行综合判断则更优。此外，仅考虑汇率自身的情况，没有纳入其他影响汇率的重要因素，模型预测结果不稳定。总的来说，本文构建ARIMA和BP神经网络模型，利用美元兑人民币汇率为数据，对未来15日汇率进行了预测分析，发现两模型对人民币汇率作短期预测是有效、可行的。该模型还可推广用于股票价格、股指、产品价格预测等方面。