两类算法生成的聚类网络的大尺度结构特征的比较

胡燕萍，李金仙，李伟强

(山西大学 数学科学学院， 太原 030006)

疾病在复杂网络上的传播已经成为疾病动力学研究的重要组成部分[1]。大量文献已经证实，网络的结构特征对疾病在其上的传播有着显著的影响，比如度分布和聚类系数等。聚类，作为现实生活中普遍存在的一种现象，一直受到很大的关注，但是研究聚类的动力学模型并不多，有关聚类的结论大多是基于网络模型给出的。目前，生成聚类网络的算法已有不少，包括迭代算法[2]、基于群体的算法[3]以及Big-V重连算法[4]等，而引人注目且应用较为广泛的是Big-V重连(BV)算法。BV算法具有适应性强、引入聚类更加随机等优势，但也存在计算成本较高的不足。本文介绍一种新的生成聚类网络的算法，这种算法是基于配置模型(configuration model)的推广[5-6]，称之为GCM算法。一方面，从某一角度研究了GCM算法的可行性；另一方面，将GCM和BV两种算法进行了对比，特别是在由它们生成的聚类网络的大尺度结构特征方面。

1 聚类介绍以及算法描述

聚类描述的是“朋友的朋友也是朋友”这类现象。聚类现象普遍存在，如在一个刻画朋友关系的网络中，一个人的两个朋友之间也极有可能彼此是朋友，即一个节点的两个邻居之间也可能存在连边。

在网络中，聚类系数是描述网络中节点聚集程度的一种度量。根据刻画尺度的不同，聚类可以给出两种不同的定义方式[7]：全局和局部的度量。全局聚类系数旨在度量整个网络的集聚性，其定义如下：

其中：NΔ表示网络中三角形的数量；N3表示网络中总的三元组的数量。局部聚类系数刻画了网络中单个节点的聚集水平，定义节点i的聚类为

其中：di表示节点i的度；Ei表示节点i的di个邻居之间实际存在的边数。

对于网络聚类而言，研究普遍集中于讨论聚类的存在给网络结构带来的差异以及对建立在网络上的动力学过程的影响。文献[8]对前人研究的成果进行了综述，指出聚类对传染性疾病的增长速率、最终规模与阈值均有不同程度的影响。除了从宏观角度上对网络整体聚类水平进行研究之外，从微观角度上，有文献也指出，即便在具有相等的全局聚类系数的前提下，网络局部聚类分布的差异也有可能影响疾病的动力学[6]。

1.1 GCM算法

随机聚类网络是基于N个节点网络中随机安排一定数量的边与三角形而生成的，其中，随机数的产生与度分布pk和参数pt有关。而网络的边则通过下述过程构造：

1) 对于每个节点v，随机安排服从于度分布pk的边数δv和服从于参数为(δv-1)δv/2与pt的二项分布的三角形数ρv，其中pt(pi∈[0,1])为一给定常数。

2) 对于每个节点v，构造一个由“半边(half-edge)”组成的集合Xv，元素为节点v的δv个副本(copies)，也构造一个由“角(corner)”组成的集合Yv，元素为节点v的ρv个副本。令X=Xv1∪Xv2∪…∪XvN，Y=Yv1∪Yv2∪…∪YvN。

3) 判断||Y||<3是否成立，如果成立，则直接跳到步骤5)。否则的话，从集合Y中随机选取3个元素v1、v2与v3后，执行如下步骤：

① 对上述3个节点中的任意两个，判断它们之间是否已存在连边。如果没有，则在它们之间构造一条边。

② 对上述3个节点，依次进行如下过程，以节点v1为例阐述：判断节点v1剩余的半边数是否小于2并且节点v1剩余的角数是否为0；如果条件成立，首先在剩余的半边与另一条随机选择的半边之间构造一条边，然后对于由节点v1的所有邻居所构成的全部可能邻居组合，只要组合中的任一邻居仍有多余的半边与角，便在它们之间构造一条边，直到所有组合都被尝试过或者节点v1的角不再剩余；最后令Yv1=∅。

③ 在整个过程中，一个包含节点v的新三角形一旦形成，则从集合Yv中删除v的一个副本；同样，一条包含节点v的新边一旦形成，则从集合Xv中删除v的一个副本。

4) 重复步骤3)。

5) 在从集合X中随机选择的两个元素之间构造新边，直到||X||<1。其中||·||表示一个集合元素的个数。

注意到GCM算法允许两个节点之间存在重边，也允许自环的情形出现，然而相较于大型的稀疏随机网络而言，出现重边与自环的情形是非常稀少的，因此可以忽略不计。此外，不难发现，如果令pt=0，GCM算法完全“退化”成配置模型。

1.2 BV算法

BV算法[4]是通过两个步骤来生成聚类网络的：第1步，生成一个随机图；第2步，通过断边重连的方式，在图中引入聚类。

断边重连也被称为边的交换。一个断边重连的过程由两步组成：一是断开两条不相邻的边，二是重新连接断开的边，见图1。在BV算法中，断边重连是基于5个节点构成的形状类似于“大V(big-V)”的网络结构进行的，见图2。这种基于“大V”的断边重连，一方面增加了网络的聚类，另一方面未改变每个参与节点的度。

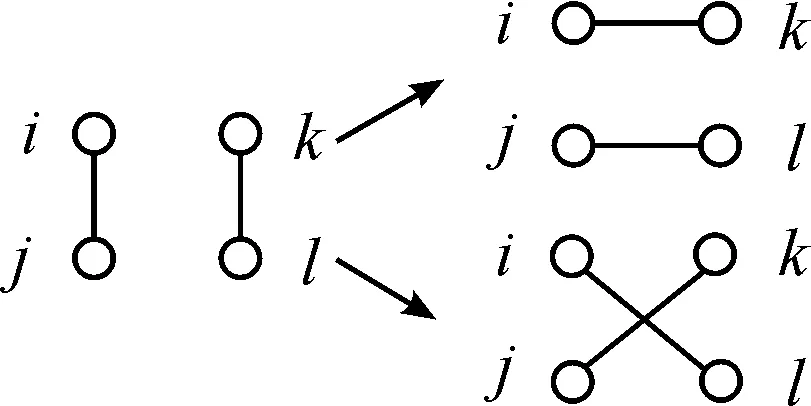
图1 断边重连示意图

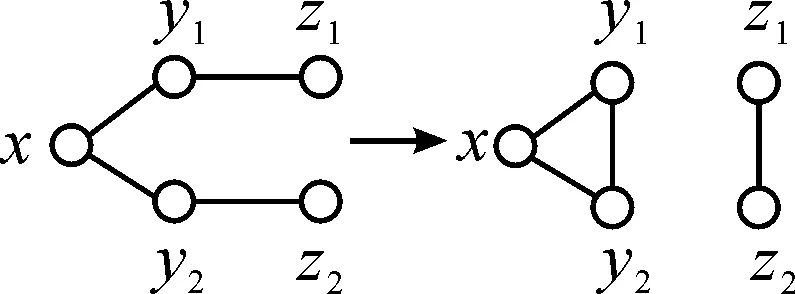
图2 “大V”断边重连示意图

2 网络的大尺度结构

为了研究两类聚类网络生成算法的差异，关注两类算法生成的聚类网络的结构特征，特别是大尺度结构特征[9]，对两种算法选取相同的初始度序列，分别生成100个网络，并使得聚类值分别为C=0.2与C=0.35。在这里采用如下一系列度量来刻画网络的大尺度结构：

2.1 路径长度

在现实网络中，很大部分节点彼此并不相连，但绝大部分节点之间经过很少几步就可以到达，这种现象也被称为小世界现象。不难想象，小世界网络对疾病的传播有着明显的影响。设想，在一个路径普遍较短的简单网络上，疾病从一个节点传到另一个节点只需要通过更少的边，进而在某些假设下，这就意味着疾病可以在较短的时间内爆发到一定的数量。

常使用下式来刻画网络的平均路径长度：

其中：dij表示网络中节点i与j的最短距离；N表示网络的总节点数。在实际使用中，常常仅在网络的最大连通片中考虑此均值，也就是说，上述求和只对最大连通片中的节点进行，N也仅表示最大连通片中节点的数量。

2.2 同配混合

同配混合是描述网络相关性的一种特征量，即网络中的节点偏向于与其类似的节点相连的倾向性。这种倾向性普遍存在，比如，在刻画朋友关系的网络中，人们偏向于和与他们有共同语言、相同爱好的人交朋友，这就是一种倾向性，此时，这个网络被视为是同配混合的。在网络中，常常关注一种倾向性——度的同配性，可以采用如下形式度量：

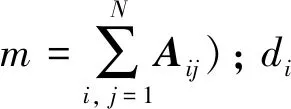
2.3 连通片规模

连通片是指网络中一些节点的集合，使得集合中的任意两节点至少有1条路径相连，其中最大的那个就是巨连通片(GCC)。本文采用边渗流的思想来研究两类算法生成的网络结构，具体而言，即通过随机删除网络中一定比例p的边来观察巨连通片规模的变化，结果对研究与控制网络上疾病的传播有着非常重要的启示[10-11]。

3 结果

为了对比两类算法生成的网络在大尺度结构特征上的差异，统一采用度分布-泊松分布来生成网络，其中：平均度n=5；网络总节点数N=104。

首先验证GCM算法的可行性。图3给出的是分别取定pt=0.22与pt=0.6的情形下，由GCM算法生成的网络的聚类系数的取值情况。从图3可以看出：就生成的网络的聚类而言，GCM算法具有良好的稳定性，从而在一定程度上证实了该算法的可行性。

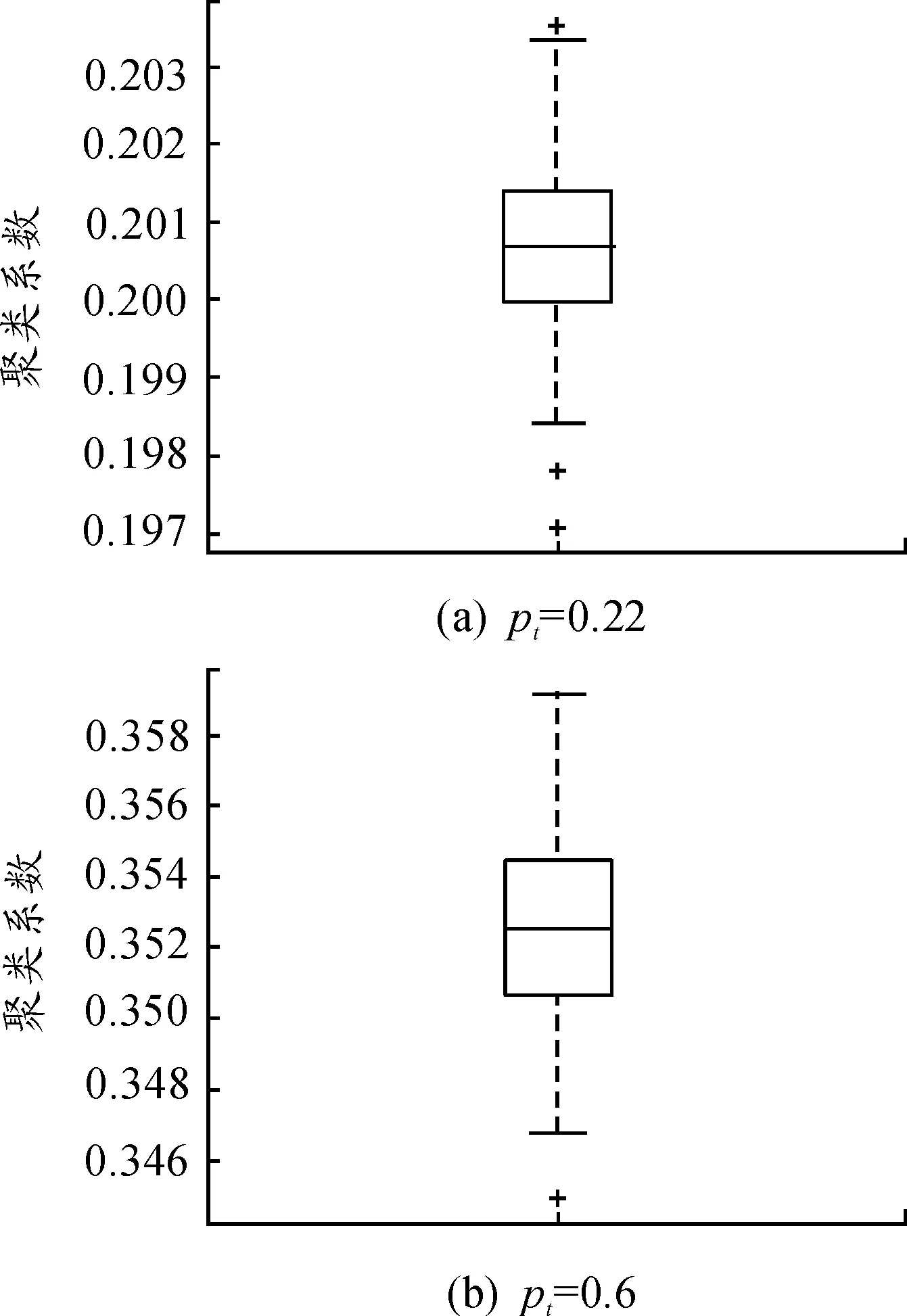
图3 在不同pt值下，GCM算法生成的100个网络的聚类系数的箱图

值得注意的是，图4表明，相较于BV算法，GCM算法以一种更同质的方式引入聚类。既然事先把网络中每个节点的局部聚类值预设为pt，那么这个结果是可以预见的。同时也注意到，在引入较高水平聚类的情形下，两种算法均会使得网络聚类分布更加异质。此外，仍需指出的是，GCM算法并不能实现对网络中每个节点的局部聚类进行预期控制，一种常见的结果就是出现局部聚类严重偏离pt的节点，如图4中用符号“+”所表示的节点，不过也正如图4所示，这种状况很少发生。

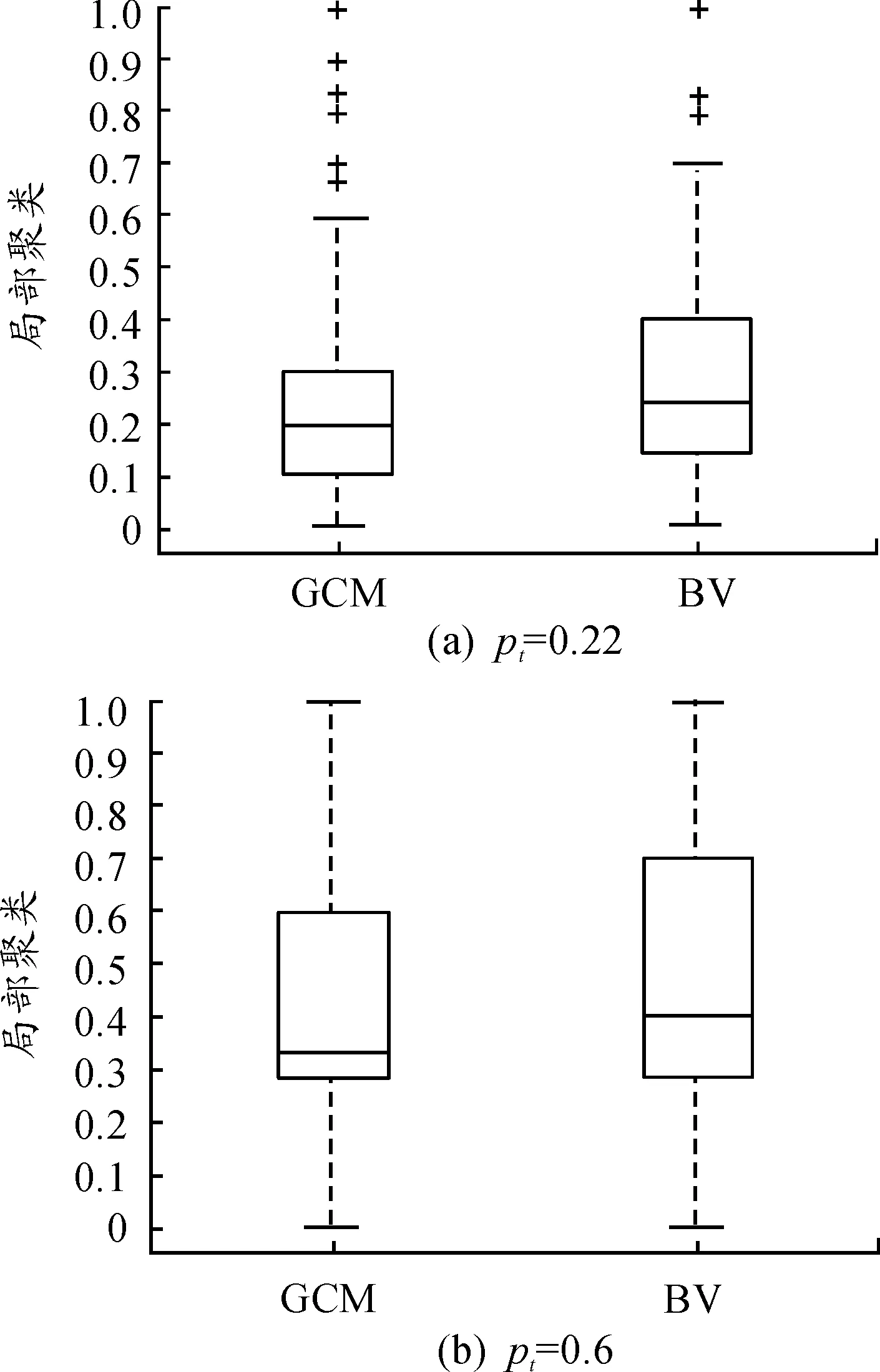
图4 不同pt值下局部聚类的分布(GCM与BV算法分别生成的100个网络的局部聚类的箱图)

在网络平均最短距离方面，在相等的聚类水平下，两类算法并没有表现出明显的差异。不过也注意到，平均最短距离会随着聚类水平的升高而增大，见表1。对此，一种可能的解释是：当网络存在较高水平聚类时，网络节点趋向于聚集成一些小的丛，使得在给定网络的度分布、网络的总边数为定值的前提下，更多的边存在于节点丛内，于是处于节点丛内外的节点间的路径长度会增大，最终平均距离随之增大。

在网络的度的同配性方面，两者却表现出了较大的差异，见表1。关于这一点，给出如下可能的解释：网络中的任一节点v出现在集合Y中的次数是近似正比于(dv-1)dv的，使得两个度较大的节点更倾向于连接在一起，因此网络会呈现出较大的度的同配性。此外，值得注意的是，聚类水平的升高并未引起网络的度的同配性发生较大的改变。另外，从表1中还可以看出，BV算法在引入较低水平聚类时并未导致网络呈现出较大的度的同配性，这是BV算法很重要的一个优势。

表1 几类网络结构特征的统计量

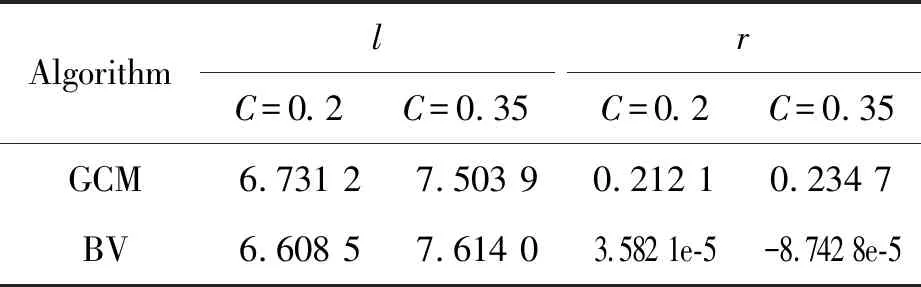
AlgorithmlC=0.2C=0.35rC=0.2C=0.35GCM6.731 27.503 90.212 10.234 7BV6.608 57.614 03.582 1e-5-8.742 8e-5

最后，在网络的恢复力方面，两类算法呈现出不同的现象。具体地说，随着聚类水平的升高，由BV算法生成的网络的巨连通片对边的移除更加敏感，特别是当边的移除比例达到一定数值时；相对而言，GCM算法则并不明显。不过，对两类算法而言，渗流阈值依旧存在，而且在不同聚类水平下，阈值并未表现出明显的不同，见图5。

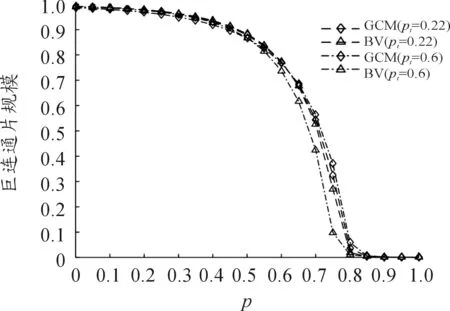
图5 不同概率下p巨连通片的规模(结果是500次值的平均，其中对100个网络中的每一个重复5次随机删边过程)

4 结束语

通过对两类生成聚类网络算法的对比不难看出，在引入较低水平聚类时，两类算法生成的聚类网络表现出诸多相似之处，因此认为GCM算法可以在一定程度上替代BV算法。当然，GCM算法自身也存在着许多不足之处，比如很重要的一点(从图3中也不难看出)，GCM算法只能引入较低水平的聚类，而BV算法就灵活得多。此外，文献[12]已经表明，不同算法生成的聚类网络在网络结构上具有很大差异，这就意味着，如果要研究疾病在聚类网络上的传播就必须考虑不同网络结构所可能带来的影响，不过目前的进展还不能给出一个令人满意的回答。