媒体报道影响下的传染病模型随机灭绝性分析
2019-06-14张培钰刘茂省
张培钰,刘茂省
(中北大学 理学院, 太原 030051)
媒体报道是一种有效控制传染病传播的途径,疾控中心将竭力阻止疾病的传播,尽快告诉人们适当的预防知识,有利于大众积极预防疾病,不仅可以影响个人对疾病的行为,而且可以采取恰当的预防措施,如社会疏远、戴防护口罩等。与此同时,任何传染病的流行都会依赖人群中容易感染的个体,疾病信息传播形成的意识活动也会导致疾病传播的性态发生改变。作为意识传播,人们对它作出反应,以至于改变他们的意识,从而通过改变他们的易感性来减小被感染的机会。基于传染病信息传播迅速的现状和信息传播对传染病预防的影响,可知建立含有信息传播因素的模型是非常有必要的。综上,更现实的方法是考虑媒体报道和疾病信息意识的相互作用。为了从数学上描述这种情况,文献[1-2]建立了研究信息传播对传染病传播的影响。
近年来,已经有很多传染病模型描述环境噪声对传染病动态的影响[3-5],如气候、卫生习惯等都会引起环境波动,这些因素可能会影响自然出生率、自然死亡率等。文献[6]对这类问题展开了研究。对于人与人之间的传染病而言,由于每个人的活动范围随时发生变化,人际交往接触也不可预测,所以本文考虑在接触率上加随机扰动具有现实意义。本文首先基于确定性模型建立了随机性模型;其次,运用文献[7-9]中的相关知识对模型的正解存在唯一性及灭绝性进行了分析;最后,用数值模拟验证这些结果的正确性。
1 模型的建立
1.1 确定性模型的建立
由于媒体对疾病进行报道,易感者对疾病产生预防的意识,从而减少与感染者的直接接触形成新的一类——有疾病信息意识的易感者。因此,整个人群可以分为3类:无疾病信息意识的易感者、有疾病信息意识的易感者、感染者,分别用X(t),Xm(t),Y(t)表示t时刻其占总人数的比例。M(t)表示t时刻关于疾病形成的意识活动的累积密度,且与感染者的人数成比例,是一个随时间变化的函数。已知在文献[2]中建立了含有时滞项λX(t)M(t-τ)的传染病模型,因此令τ=0,建立不含时滞的模型,可得系统(1):
(1)
其中,假设b是所考虑地区的易感者的移民率,疾病只有通过易感者与感染者的直接接触才能传播。β是无意识的易感者与感染者的接触率,d是自然死亡率,μ是媒体的执行率,μ0为媒体的耗散率,m0为爆发疾病的其他地区的信息传播对本地区的影响,λ是指意识在无意识的易感者中的传播率,λ0指有意识的易感者转变成无意识的易感者的死亡率,ν指感染者的恢复率,q指进一步假设恢复为有意识的易感者的比例。有X(0)=X0>0,Xm(0)=Xm0≥0,Y(0)=Y0>0,M(0)=M0≥m0模型里的所有参数为正数。
模型的吸引域为:
1.2 随机性模型的建立
在现实社会中,媒体报道的传染病模型会受到环境噪声的影响,使用随机模型可以更准确地预测系统将来的动力学行为。因此,本文假设接触率β和传播率λ会受到随机波动的影响,即β→β+σ1dB1,λ→λ+σ2dB2,假设恢复者恢复为易感人群,X表示易感人群,Y表示感染人群,Xm表示有意识人群,令m0=0,B(t)是带有B(0)=0的标准布朗运动,σ2>0表示白噪声的密度。媒体报道影响的随机传染病模型可以表示如下,即系统(1)可简化为系统(2):
(2)
2 正解的存在唯一性
为了研究传染病模型的动力学行为,首先需要注意解是否为全局正解。接下来证明全局正解的存在唯一性,这是探究模型长期行为的先决条件。系统(2)的系数满足局部Lipschitz连续条件,但没有满足线性增长条件,因而系统(2)的解有可能在有限时间内爆发。本节中,我们用Lyapunov分析方法证明系统的解是全局正解。
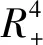
证明由于系统(2)的系数满足局部Lipschitz条件,因此对任意给定的初值(X(0),Xm(0),Y(0),M(0)),在t∈[0,τe]时,有唯一的局部解(X(t),Xm(t),Y(t),M(t)),这里τe是爆发时刻。要证明(X(t),Xm(t),Y(t),M(t))是全局解,需证明τe=∞。令ε0>0,使得初值(X(0),Xm(0),Y(0),M(0))>ε0,对于任意的ε≤ε0,我们定义一个停止时刻:
τε=inf{t∈[0,τe]:X(t)≤ε或Xm(t)≤ε或Y(t)≤ε或M(t)≤ε}
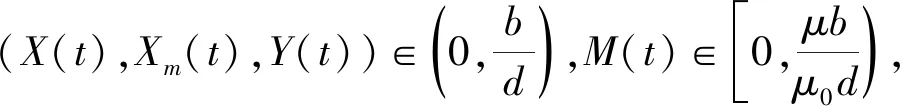
对上述式子两边积分,可以得到:
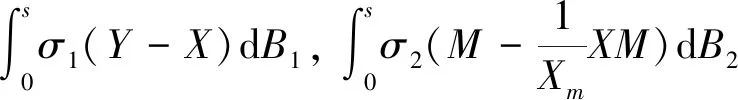
EV1(X(t∧τε))≤V1(X(0),Xm(0),Y(0),M(0))+K(t∧τε)≤V1(X(0),Xm(0),Y(0),M(0))+Kt
另一方面,由V1(X(t∧τε))>0可以推出:
EV1(X(t∧τε))=E⎣χ(τε≤t)V1(X(t∧τε))」+E⎣χ(τε>t)V1(X(t∧τε))」≥E⎣χ(τε≤t)V1(t∧τε)」
(3)
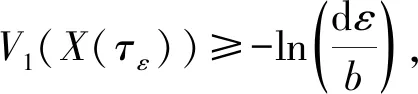
(4)
结合式(3)(4),对所有的t≥0有:
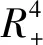
3 疾病的灭绝性
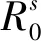
定理3.1如果R0<1,(Xm(t),Y(t),M(t))几乎处处收敛(0,0,0)。
证明令(Xm(0),Y(0),M(0))∈Ω,因为R0<1,令η>0使得
设V2(t)=ln(Y(t)+Xm(t)+ηM(t)),根据多维It公式,可得:
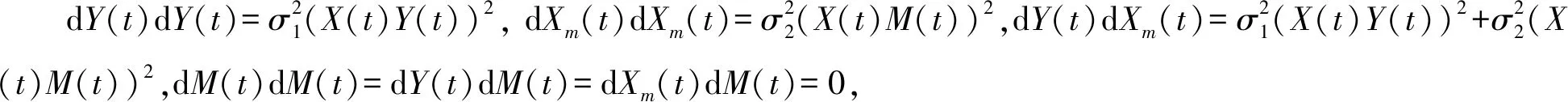
对上述式子两边求积分可得:
ln(Y(t)+Xm(t)+M(t))≤ln(Y(0)+Xm(0)+ηM(0))-pt+
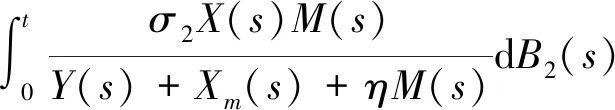
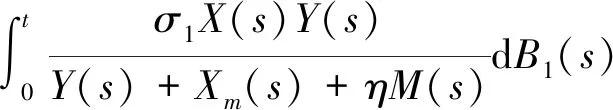
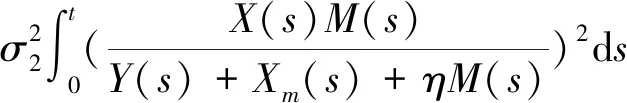
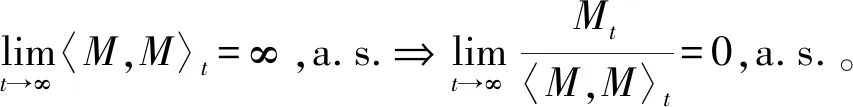
引理2(非负半鞅收敛定理)[11]设X(t),A(t),B(t)均为实值连续适应过程,N(t)是一个实值连续局部鞅,A(0)=B(0)=N(0)。ξ是一个非负可测的随机变量,定义
X(t)=ξ+A(t)-B(t)+N(t)
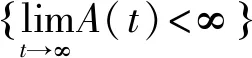
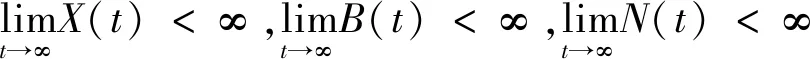
也就是说,随机过程X(t),B(t),N(t)收敛于有限随机变量。
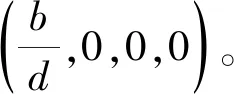
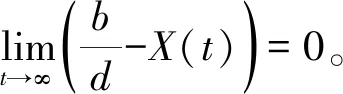
两边同时积分可得:
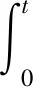
由定理3.1可得:
由引理2可得:
(5)
由定理3.1可得:
(6)
由式(5)和(6)可得:
(7)
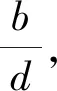
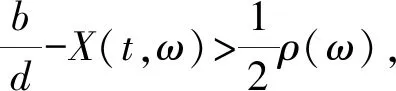
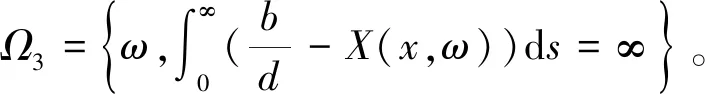
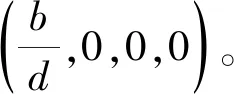
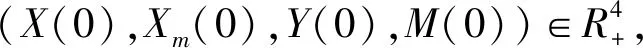
证明利用It公式得出,
左右两端从0到t积分可得,
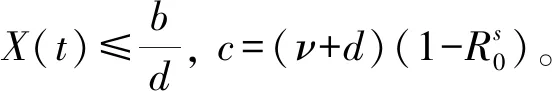
4 数值模拟和讨论
本节利用数值模拟的方法分析随机模型(2)无病平衡点的动力学性质。图1~4是当R0<1时随机性模型与确定性模型解的对比图,可以看出在噪声强度比较小时,系统(2)的解在其确定性模型的无病平衡点E0附近随机波动。
本文主要分析了媒体报道影响下的传染病模型的随机灭绝性,通过Lyapunov分析方法和It公式证明了模型存在唯一的全局正解,接着运用非负半鞅收敛定理,证明了当R0<1时,系统几乎处处收敛,并且给出了随机基本再生数和疾病灭绝的关系。通过数值模拟得知:当噪声强度小时,基本可以忽略噪声的影响,确定性模型和随机性模型差别不大。
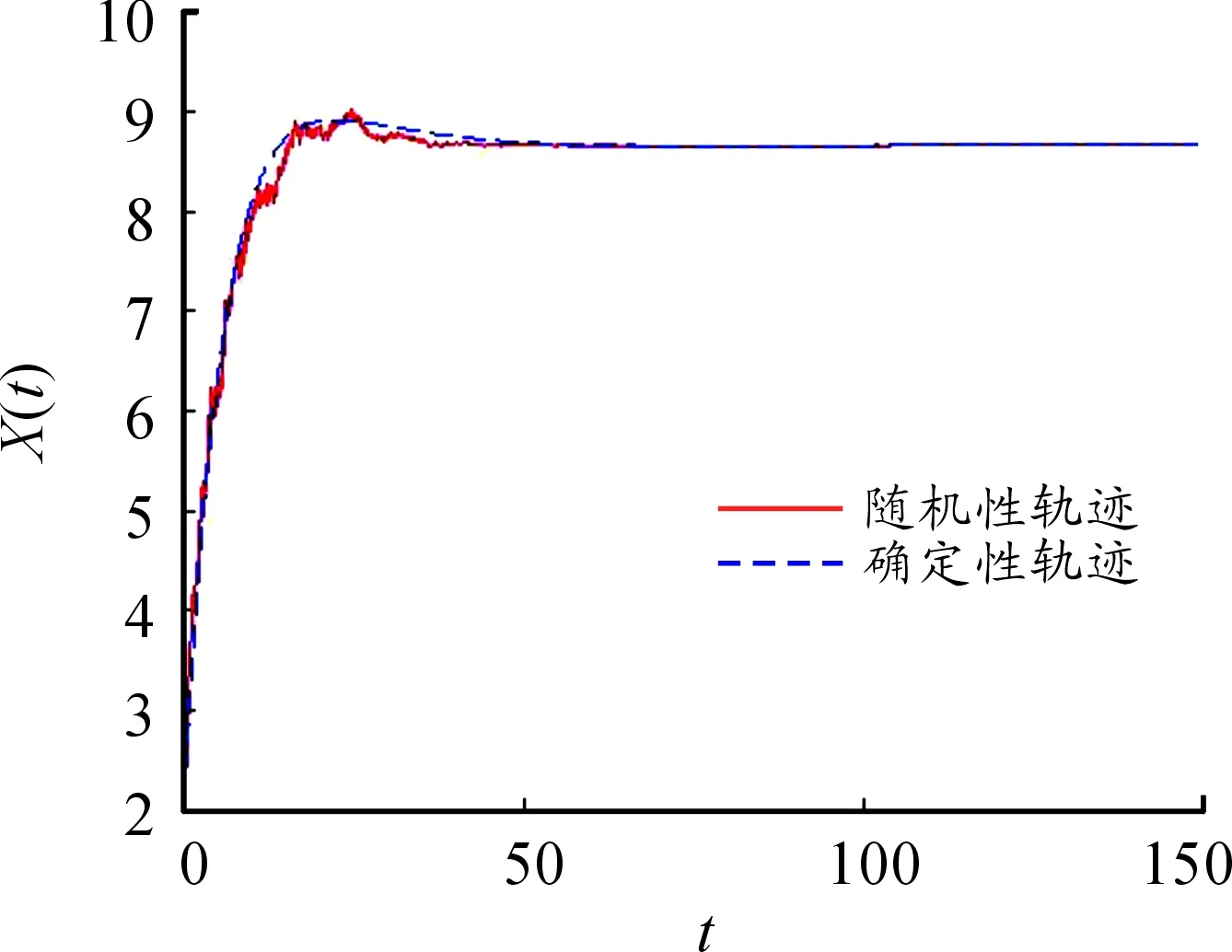
图1 无疾病信息意识的易感者

图3 感染者
图中所取参数b=0.5,β=0.002,μ=0.005,d=0.06,σ1=0.01,σ2=0.03。
