大数据挖掘中的混合差分进化K-Means无监督聚类算法

吴雅琴，王晓东

(内蒙古医科大学 计算机信息学院， 呼和浩特 010110)

近年来，随着计算机和互联网技术的快速发展，人们在工作和生活中产生了各种形式的数据，如文本、图像、音频、视频等，这些数据的存储量正变得越来越大。如何准确和有效地从这些海量数据中抽取出隐藏的、有价值的信息成为计算机科学领域中的研究热点，由此数据挖掘技术应运而生[1-2]。数据挖掘又称知识发现，即“从数据中挖掘知识”，可以看作信息技术自然进化的结果。聚类分析作为大数据挖掘中最为重要的方法之一，已经得到了人们越来越多的关注[3]。其中，K-Means无监督聚类算法是现有聚类算法中最为典型的划分算法。目前，K-Means聚类算法在情报检索、机器学习、专家系统(依靠过去的经验法则)和模式识别等领域得到了广泛应用[4]。

K-Means聚类算法作为聚类分析中广泛应用的一种经典算法，具有算法结构简单、运行效率高且适用范围大等优点。文献[5]将基于K-Means聚类算法的自动图谱识别应用于电缆监测，其能够对内部放电、沿面放电和干扰信号做出准确的判断。文献[6]提出了一种K-means聚类算法，并将其应用于大数据图像检索，获得了较高的检索准确率。但是，K-Means聚类算法对初始参数设置有较大的依赖性，此外，其聚类结果的鲁棒性较低且易陷入局部最优解。因此，许多文献对K-Means聚类算法进行了改进和优化[7-10]。这些方法在一定程度上克服了K-Means聚类算法的缺陷，但仍需继续优化和完善。

为了解决上述问题，提高K-Means聚类算法的聚类稳定度和速度，本文提出了一种改进的混合差分进化算法，并将混合差分进化算法引入K-Means聚类中。通过个体适值函数把种群视为2个子种群的混合体，按照不同的变异策略和参数对2个子种群分别进行动态更新，提高了获取全局最优的概率。该算法较好地解决了K-Means聚类算法容易陷入局部最优陷阱的问题。实验结果表明：相比K-Means聚类算法、基于差分进化的K-均值聚类算法，本文方法较好地提高了聚类的有效性和稳定性。

1 K-Means聚类算法基本原理

1.1 算法基本思想

作为一种基于距离的聚类划分算法，K-Means聚类算法具有结构简单、运行效率高且适用范围大等优点[4]。K-Means聚类算法一般通过如式(1)所示的目标函数来实现优化。

(1)

可以看出，式(1)所示的目标函数是一个误差平方和计算过程。其中：E为聚类准则函数；K为聚类的总数；Cj,j=1,2,…,K为聚类中的簇；x为簇Cj中的一个聚类目标；mj为簇Cj的平均大小。通常来说，E值越小则聚类效果越好。反之，E值越大则聚类质量越差。

1.2 K-Means聚类算法的基本流程

K-Means聚类算法的输入参数为数值K和数据集X中聚类目标的数量n，输出为使聚类准则函数E达到最小的K个聚类。K-Means聚类算法的基本流程如图1所示。

1.3 K-Means聚类算法存在的问题分析

K-Means聚类算法的主要缺点分为3个方面[3]：① 初始参数依赖性较高，且算法容易产生局部最优解；② 容易受噪声数据和离群数据点的干扰；③K-Means聚类算法作为一种基于欧式距离的硬聚类算法，仅对球形状簇表现出较好的聚类性能。④ 对聚类数目K的值较为敏感。针对上述缺点中的局部最优解陷阱问题，本文引入差分进化算法，并与K-Means聚类算法进行结合。

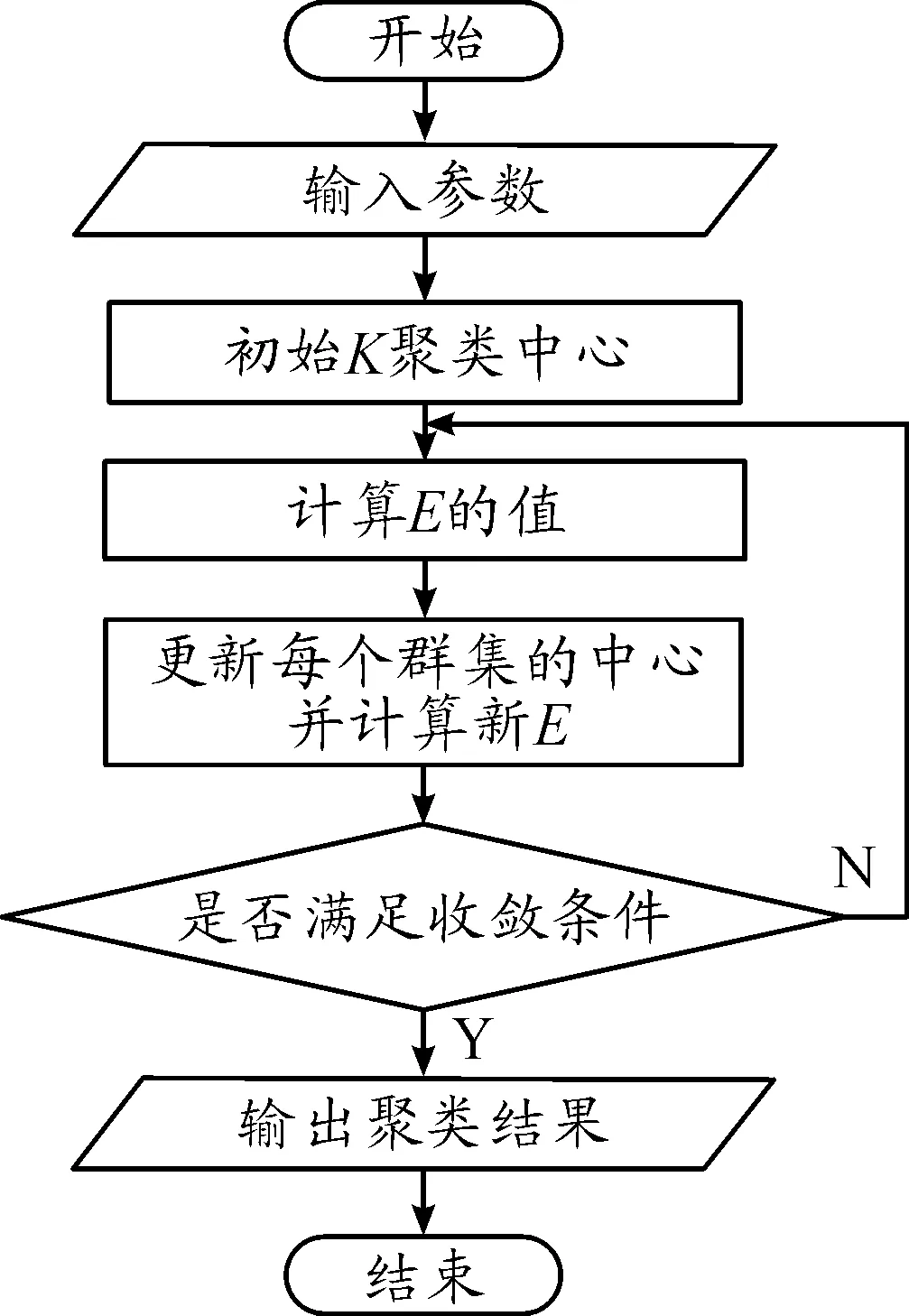
图1 K-Means聚类算法流程

2 差分进化算法

差分进化算法是一种基于群体智能的新型启发式算法，能够通过演化技术计算种群中个体间的差异信息，并按照适应值的结果择优选择符合要求的下一代种群，从而完成种群的进化[11]。差分进化算法是一种具有良好稳健性和全局搜索能力的全局优化算法[12]。

设X为初始种群，N为种群的大小，Xi(t)(t=1,2,…,N)为当前种群中进化个体，t为进化过程的迭代次数。种群中个体变异操作的过程如式(2)所示。

Vi(t)=(vi1(t),vi2(t),…,viD(t))=

Xp1(t)+F(Xp2(t)-Xp3(t))

(2)

其中：Xp1(t)、Xp2(t)、Xp3(t)是从当前进化种群中随机选择的3个不同个体；F是缩放权值。经验表明：F=0.6时效果较好；D为种群中个体的维度，即变异个体Vi(t)由D个分量构成。

当前种群中的进化个体Xi(t)与Vi(t)进行交叉操作，生成竞争个体Ui(t)=(ui1(t),ui2(t),…,uiD(t))(由D个分量构成)。竞争个体Ui(t)中j-th分量的计算方法如式(3)所示。

(3)

其中：z是一个随机整数，且z∈{1,2,…,D}；CR∈[0,1]，为交叉概率，经验表明，CR取值在0.3～0.9较为适宜。

通过适应度值对比竞争个体和当前种群中的进化个体，并按照式(4)方法在上述两者中进行择优选择更新种群[13]。

(4)

3 混合差分进化K-Means聚类算法

在种群的迭代进化过程中，根据贪婪选择策略，传统的差分进化算法会以较大的概率阻止适应度较差的个体进入下一代种群。这种情况会造成迭代末期时种群个体之间的差异较小，多样性较低，容易导致种群中大多数个体都集中在一个局部极值点附近。这种情况下，无论如何进行变异、交叉和选择，进化后的种群都与上一代种群十分类似，无法产生新的个体。针对该情况，本文通过个体适值函数把种群视为2个子种群的混合体，并按照不同的变异策略和参数对2个子种群分别进行动态更新，提高了获取全局最优的概率。

3.1 混合差分进化算法

首先按照参数δ对种群进行划分，前δ%个个体为子种群X′，其余个体为子种群X″。在每次迭代进化的最后，根据式(5)更新参数δ。

δ=δmin+rand·(δmax-δmin)

(5)

按照不同的变异策略和参数对2个子种群分别进行动态更新。对于子种群X′中个体Xi(t)，采用的变异策略如式(6)所示。

Vi(t)=Xi(t)+Fi(t)·(Xp1(t)-Xp2(t))+

Fi(t)·(Xp3(t)-Xp4(t))

(6)

其中：Fi(t)为个体Xi(t)相应的缩放权值；Xp1(t)、Xp2(t)、Xp3(t)、Xp4(t)是从当前进化种群中随机选择出来的4个不同个体。

对于子种群X″中个体Xi(t)，采用的变异策略如式(7)所示。

Vi(t)=Xi(t)+Fi(t)·(Xδbest-Xi(t))+

Fi(t)·(Xp5(t)-Xp6(t))

(7)

其中：Xδbest为从子种群X′中随机选择的个体；Xp5(t)、Xp6(t)是从当前进化种群中随机选择出来的2个不同个体。

对于子种群X′和X″中的个体Xi(t)，若通过Fi(t)生成的后代能够进入下一代，则记录到集合SF中，下一代个体Xi(t+1)对应的缩放权值可以按照式(8)产生，否则按照式(9)产生。

(8)

(9)

其中：fiti为当前个体的适应度值，fitb为当前种群中个体的最佳适应度值，fitw为当前种群中个体的最差适应度值；meanA(SF)为集合SF中所有对象的算术平均值。

按照以上缩放权值的动态更新方法，能够充分考虑所产生后代存活情况。这种按照不同的变异策略和缩放权参数对2个子种群分别进行动态更新的方法可有效提高获取全局最优的概率。

3.2 基于混合差分进化的 K-Means聚类算法

基于混合差分进化的K-Means聚类算法流程如图2所示。

4 实验结果与分析

为了验证提出的混合差分进化的K-Means聚类算法的性能，将本文算法与另外2种典型聚类算法(K-Means聚类算法和基于差分进化的K-均值聚类算法)进行对比，以验证本文算法的聚类性能。仿真环境为 Matlab 7.0，实验平台为Windows 10 64位操作系统，CPU为i5-4570处理器，4 GB内存。实验使用的数据集是UCI 数据库中的3个数据集，如表1所示。实验参数设置如表2所示。

表1 实验数据集参数

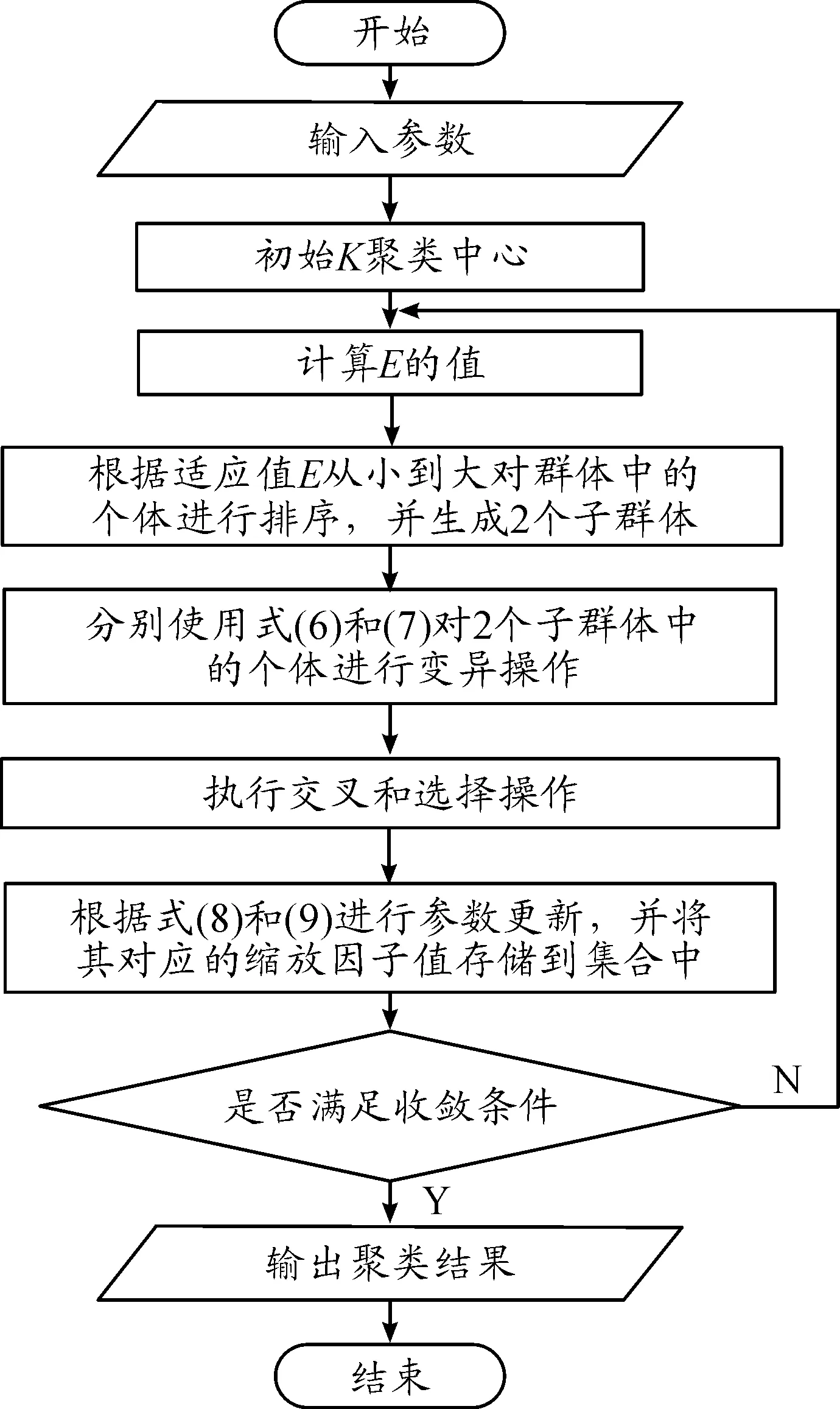
图2 基于混合差分进化的 K-Means聚类算法流程

参数数值种群规模40λmax0.4λmin0.2初始缩放权重 Fi(0)0.6CR0.2D20The maximum number of iterations2 000

IRIS、Glass和Vowel数据集，实验结果见表3～5。图3为20维的收敛特性。

通过表3～5可以看出，在最小类内距离和最大类内距离结果方面，相比其他两种算法，本文算法的数值结果均为最小。这表明本文方法的最大类内距离和最小类内距离之间的差值都有较大的减少。此外，本文方法具有最小的平均类内距离，说明聚类结果波动范围较小，稳定性较高。

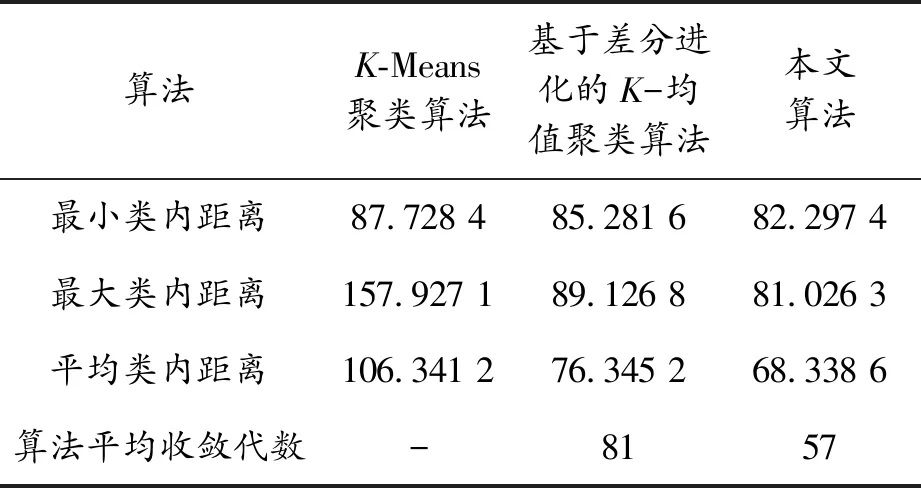
表3 IRIS数据集的实验结果

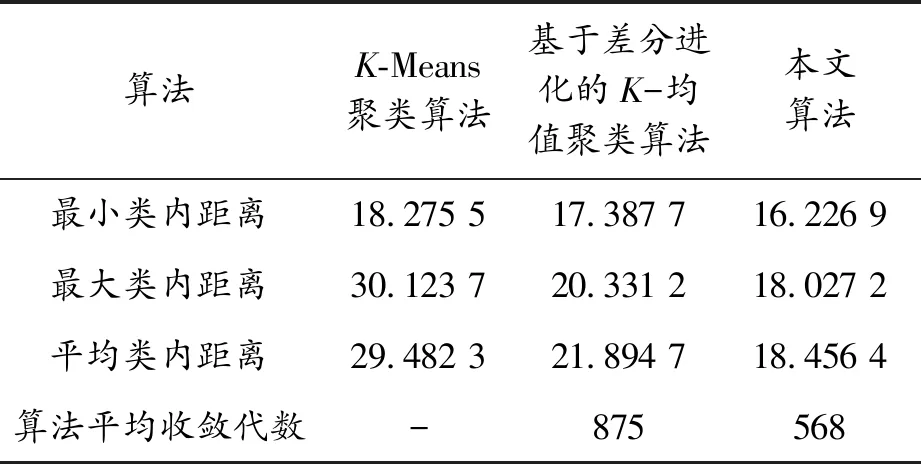
表4 Glass数据集的实验结果

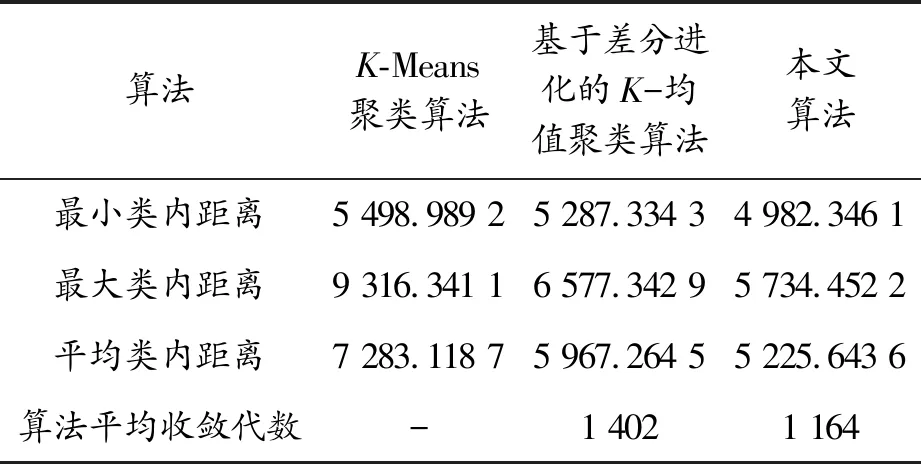
表5 Vowel数据集的实验结果

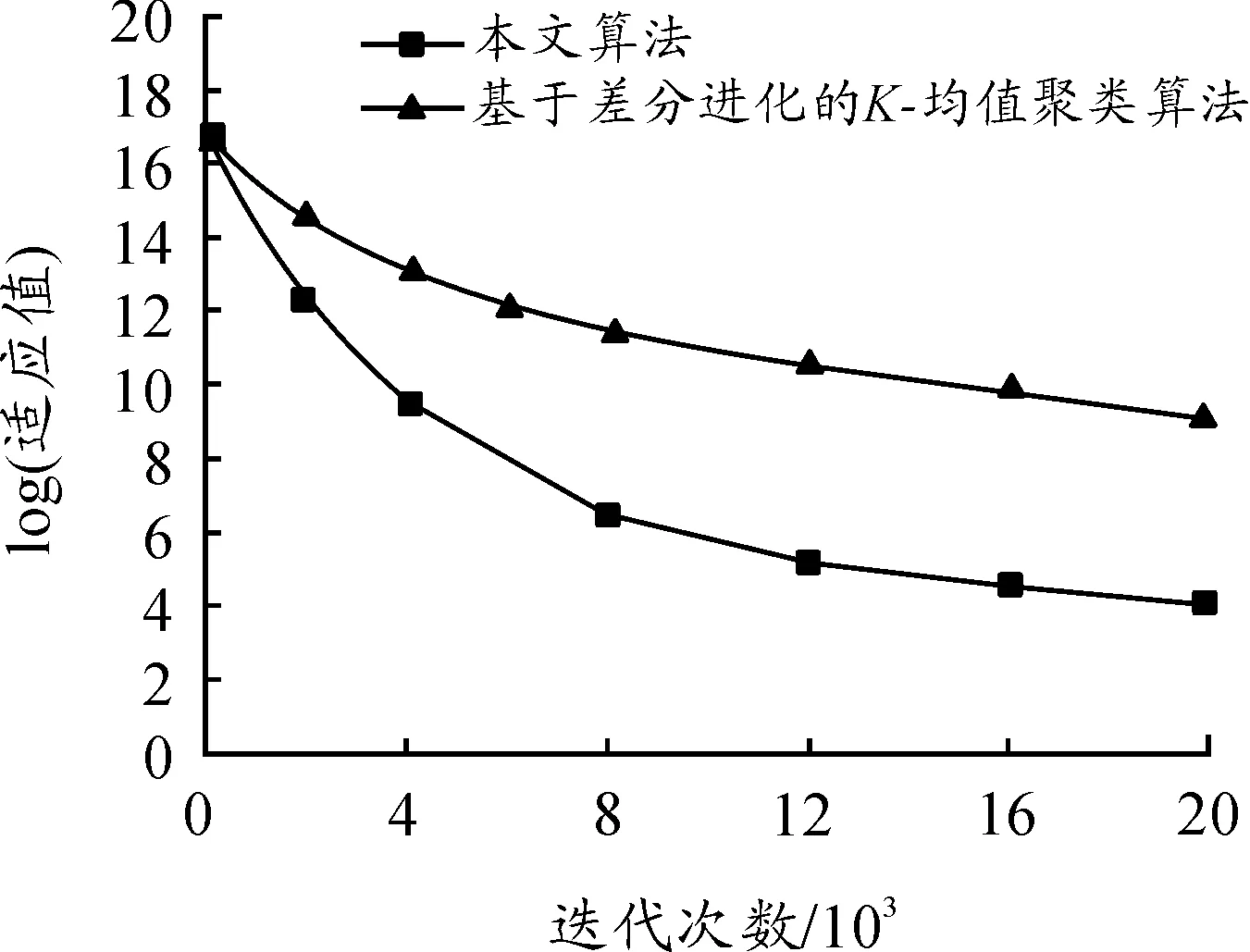
图3 收敛特性比较

在算法平均收敛代数方面，相比基于差分进化的K-均值聚类算法，本文算法的收敛速度有所提升，这是因为采用了双种群混合策略。图3的曲线结果也验证了本文算法的收敛优势，表明其具有良好的寻优能力。

上述实验结果验证了本文算法的可行性和高效性。相比其他两种算法，本文算法能以较快的速度获得全局最优值，并具有更好的鲁棒性。

5 结束语

本文提出了一种改进的混合差分进化算法，并将混合差分进化算法引入K-Means聚类中。通过个体适值函数把种群视为2个子种群的混合体，并按照不同的变异策略和参数对2个子种群分别进行动态更新，提高了获取全局最优的概率。该算法较好地解决了K-Means聚类算法容易陷入局部最优陷阱的问题。实验结果表明：相比K-Means聚类算法、基于差分进化的K-均值聚类算法，本文方法能有效提高聚类质量和收敛速度。