基于FPGA的TDC系统偏差修正方法的研究*

刘正阳，刘音华,3，李孝辉,3,4

(1.中国科学院 国家授时中心，西安 710600；2.中国科学院大学，北京 100049；3.中国科学院 时间基准频率重点实验室，西安 710600；4.中国科学院大学 天文与空间科学学院，北京 101048)

0 引言

TDC(time-to-digital converter)是将时间间隔模拟量转换为数字量的一种时间数字转换器[1]。随着科技的高速发展，时间数字转换器已广泛应用于高能物理实验、通信、卫星导航等诸多领域，且根据不同的应用场合，对其测量精度也提出了越来越高的要求。

为了提升时间数字转换分辨率，当前的主流方法大致分为两种，一种是将待测时间“放大”，在现有的分辨率下进行测量，比如时间延展法；另一种是寻找尽可能小的时间分度来测量时间间隔，比如时间内插法。

利用延迟链技术的时间内插方法，因其可以实现较高的时间精度，近些年来得到迅速的发展和应用[2]。插值法将大步长计数和精密测量结合起来，既能获得较大的动态范围，也能达到较高的时间精度。对于插值法，延时单元的一致性、精确度决定了TDC的时间分辨能力。

目前高分辨率的TDC主要是在ASIC芯片上实现的，但ASIC芯片价格昂贵，开发周期长。而基于FPGA(field-programmable gate array)芯片实现的TDC成本低，开发周期短，设计灵活，近年来受到广泛关注[3]。

但是，基于FPGA芯片实现的TDC存在着较大的系统偏差，以基于FPGA加法进位链的时间间隔测量系统为例，FPGA的工艺、仪器偏差、外部硬件电路的走线等都影响着测量结果。而这些偏差对于高精度时间间隔计数器而言，将会产生明显的影响。

因此为了提高时间间隔测量系统的性能，对时间间隔测量系统的系统偏差进行校准是十分重要的，本文以Altera公司的Cyclone IV EP4CGX150DF31C7为实验芯片，通过实验分析得出了系统偏差修正的合理方案，并计算出不同参考时钟下的系统偏差拟合模型，进一步提高测量的准确度。

1 时间间隔测量原理

本文所研究的计数器采用的时间间隔测量基本思路如图1所示，为兼顾量程和测量分辨率，将测量分为粗测量和细测量两部分。

首先，粗测量测量起始信号和截止信号的时间间隔，由起始信号开门，以截止信号关门，在此时间段内，时基脉冲进入计数器，若时基脉冲周期为TP，计数器指示值为N，则待测时间间隔粗测量结果为NTP[4]。

待测时间间隔的细测量包括两个部分，一是测量开始信号上升沿相对于下一个基准时钟上升沿之间的时间间隔ΔT1，另一个是测量截止信号上升沿相对于下一个基准时钟上升沿之间的时间间隔ΔT2，本文所设计基于FPGA内部加法进位延迟链资源实现时间的精密内插，从而实现ΔT1和ΔT2的细测量[5]。

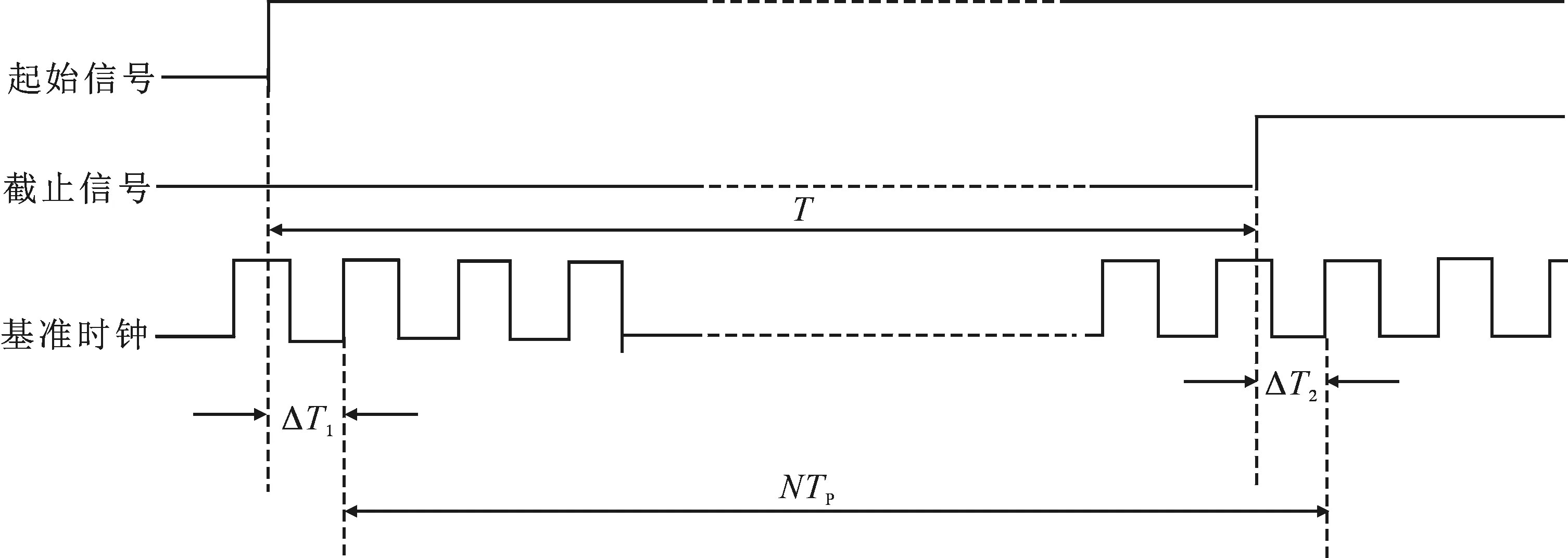
图1 时间间隔测量基本思路

细测量的基本延迟单元由加法进位延迟链构成，通过对延迟单元的个数进行计数再乘以平均延迟即可获得测量结果。以测量起始信号上升沿相对于下一个基准时钟上升沿之间的时间间隔ΔT1为例，如图2所示，在FPGA内设计一个串行多位加法器将专用进位链级联，第一级加法器的两个输入端分别接Start信号和一个高电平信号，其他加法器的两个输入端一个接高电平，一个接低电平，当Start信号上升沿到来，进位信号就能在所构建的进位链中传播，通过一组D触发器捕捉时钟CLK上升沿到来时刻进位信号所在的位置。如果进位链上每个延时单元的延时已知,就可以求得Start上升沿和下一个的CLK上升沿之间的时间间隔。本文所构建的加法进位链级数为96级，各进位单元时延不完全相等，每级时延在30～68 ps之间，平均延时为42 ps，因此可以实现100 ps以下的测量分辨率。

图2 细测量的基本原理

在计算各级进位链时延的过程中，CLK信号到每个D触发器时延的影响主要集中在第一级进位链，这是因为CLK信号到每个D触发器的时延相同，当信号传播到第N级(N>1)进位链时，可以通过与信号传播到第N-1级进位链的时延进行计算，得到抵消了CLK信号到D触发器时延的第N级进位链的时延，而第一级中CLK信号到D触发器时延则计入到第一级进位链时延中。由于测量截止信号与时钟上升沿之间ΔT2的时间间隔原理与起始信号相同[6]，因此在计算时间间隔测量结果T=NTp+ΔT1-ΔT2时，这部分时延也在计算ΔT1-ΔT2的过程中抵扣，因此CLK信号到每个D触发器的时延对测量结果不会产生影响。

2 基于FPGA的TDC的设计与测试平台搭建

本文中提出的FPGA设计在友晶公司的DE2i-150开发板上实现，系统程序采用Verilog HDL语言。如图3为开发板正面图示，所使用的Altera公司的Cyclone IV EP4CGX150DF31C7为图中右侧所圈注示意的。开发板上配有SMA连接件，可支持外部参考时钟的输入。

基于FPGA的时间间隔测量系统的设计构架如图4所示。工作时钟由外部输入或板载晶振产生的10 MHz参考时钟进行倍频产生，输入到FPGA开发板的数模转换电路，选用高稳定度的原子钟可以有效地保证参考时钟信号的频率稳定度。具体实现时采用锁相环对输入的10 MHz参考时钟进行倍频，输出稳定的125 MHz系统工作主时钟。同时，锁相环模块还需产生250 MHz的粗计数时钟。锁相环所产生的本片FPGA工作所需的系统主时钟，是所有模块工作的基础[7]。

在开始测量前，信号整形电路实现对待测的开始和截止信号进行整形、滤波和模数转换，转换成稳定的数字信号后送给FPGA的测量起始信号与截止信号引脚，组成两路测试通道进行时间间隔测量。

根据上节时间间隔测量原理，本文所设计的时间间隔测量系统的测量功能采用粗测量和细测量相结合的思路。粗测量的工作时钟频率为250 MHz，周期为4 ns，位宽为28 bit，可以满足1 s的量程指标要求，此时误差在正负1个时钟周期。分辨率主要由细测量模块的加法进位延迟单元的时延所决定，因此采用基于FPGA进位链的细测量模块来对1个时钟周期内的时间间隔进行测量，把测量误差控制在1个时钟周期以内。

图3 开发板正面示意图

图4 基于FPGA的时间间隔测量系统设计架构框图

校准模块采用4 MHz晶振作为校准信号的产生源，校准晶振的输出频率为4 MHz，为加法进位延迟链提供校准信号，产生相对于FPGA内部工作时钟的随机脉冲信号，采用码密度测试方法对加法进位延迟链进行校准，减少细测量模块的测量误差。

时间间隔测量系统在工作时，通过主控模块实现与FPGA的通信[8]。根据不同情况下的功能所需，CPU采用两种接口方式实现与FPGA的数据通信，一种为寄存器寻址方式，使FPGA和CPU均可以访问、读写，存储内容包括FPGA时间间隔测量结果，CPU向FPGA发送的各项指令数据等等。CPU和FPGA另一种接口方式为信号管脚直连方式，包括各种中断信号和FPGA的全局复位信号。FPGA片内的各个模块的测试，主要由Quartus II的逻辑分析仪SignalTap 来实现数据采集和分析，使用QuartusII软件可以在任何时间重新配置FPGA。

为了进一步减少基于FPGA加法进位链的时间间隔测量系统的测量误差，提高测量精度，故在得到测量结果后仍需对其进行偏差校正，为得出有效的系统偏差校准方案，搭建了如图5所示的测试平台。

图5 时间间隔测量系统测试平台连接示意图

移相电路板用于产生待测时间间隔，其工作芯片为EPM240T100C5N，上电后通过运行在通用计算机上的程序来控制产生不同的待测时间间隔。其最小步进为100 ns，产生时间间隔范围为100～999，999，900 ns。

测试开始时需首先对待测时间间隔进行标校，标校所使用的仪器为美国斯坦福公司的SR620时间间隔计数器，SR620在时间间隔测量方式下单次时间分辨率为25 ps,最小有效数据为4 ps。因其是当前国际主流时间间隔测量仪器，测量精确度高于所设计计数器，故将其测量输出的结果作为待测时间间隔的测量参考真值。

标校开始时，首先使用移相电路板产生已知时间间隔，将待测通道的开始与截止信号分别接入SR620进行测量，均取1 min的观测平均值作为该时间间隔的参考值。

将待测信号接入FPGA板，为了消除毛刺防止误检，输入信号首先需经过信号整形模块进行预处理,然后将整形后的起始信号与截止信号输入到粗测量模块和细测量模块，对计数器的各通道进行测量，每个时间间隔采样时间均为1 min。测量结果按照规定的格式经串口程序输出到通用计算机[9]。

通用计算机作为FPGA开发板和数据采集软件等的运行平台，每当FPGA加电时就可以实现与FPGA的通信。运行在计算机上的程序对数据进行解算处理，按照测量原理得到实际测量结果，与参考值进行比对，分析系统偏差[10]。

3 系统偏差的来源与修正方法

对于基于FPGA加法进位链的时间间隔测量系统来说，仪器偏差一个主要来源是延迟链的延迟单元，因FPGA中的进位链或其他逻辑资源形成的延迟单元都不是十分稳定，另外型号不同、速度等级不同也会影响延迟，除此之外，由于生产制造工艺的影响，即使是同一型号的器件的延迟也一定存在着差异。

除了FPGA芯片，外部电路的走线、测量过程的准确性同样影响着测量结果。例如开始信号、截止信号在外部硬件电路中的走线延迟不可能完全相等，测量和校准过程等存在不确定性，这些都会在最后的测量结果中引入系统偏差。

硬件线路的走线延迟与进位链引入的偏差属于稳定的系统差，可以通过测量已知时间间隔来修正。实验发现TDC工作时钟漂移引入的偏差并不是一个常量，随着待测时间间隔的变化而变化，这种现象在高精度的TDC工作时钟下并不明显，例如氢钟、铯钟，但是对于铷钟或是晶振作为工作时钟时，随着测量时间间隔增加将表现得非常明显。

为了得到有效的偏差修正方案，在测量范围0～1 s内对一系列时间间隔进行测试，对系统偏差进行分析。

图6为铯钟作为TDC工作时钟时的不同待测时间间隔的系统偏差图，图中所示为取双对数坐标后的结果，纵坐标为系统偏差，横坐标为待测时间间隔。此时偏差主要分布在350～650 ps之间左右，偏差平均值为514 ps，由图可看出二者之间存在着线性关系。

图6 铯钟作为TDC工作时钟时的系统偏差

图7为铷钟作为TDC工作时钟时的不同待测时间间隔的系统偏差双对数坐标图，此时系统偏差分布在200～900 ps之间，系统偏差平均值为555 ps。可以看出相比于铯钟，随着待测时间间隔的增加，铷钟系统偏差的增大趋势更为明显。

图7 铷钟作为TDC工作时钟时的系统偏差

由此可知，TDC工作时钟的准确度对TDC测量偏差有直接贡献，为降低不同准确度的工作时钟对TDC系统偏差的影响，提出一种线性拟合校准系统偏差的方法。在一次线性拟合中，对于硬件电路延迟等引起的系统偏差将在常数项中得以校正，TDC工作时钟的影响主要由一次项系数进行校正。

4 系统偏差校正方案验证

为验证校正方案的有效性进行了以下3组实验：首先以铯钟作为工作时钟在量程范围内选取不同时间间隔进行测试并得出一次拟合模型，其次以铷钟作为工作时钟在量程范围内选取不同时间间隔进行测试并得出一次拟合模型，最后选取任意时间间隔对不同工作时钟下的一次拟合模型进行验证。

根据所测得的样本数据通过最小二乘的方法建立一次模型，对于铯钟来说拟合的直线方程为y=7.38×10-11x+486，其斜率为7.38×10-11。根据方程求出拟合后的系统偏差修正量，得到修正后的系统偏差，表1为以铯钟作为TDC工作时钟时的0～1 s测量范围内不同待测时间间隔的系统偏差与修正后结果的对比，通过一次线性拟合，将系统偏差降至100 ps以下。整个区间所有测试值的系统偏差拟合修正后的结果如图8所示，此时整个测量范围所有测试值的系统偏差平均值为39 ps。本文中所有系统偏差均指实际测量值减去标校真值的结果，在对数坐标系中作图时负值使用绝对值表示。

表1 以铯钟作为TDC工作时钟时拟合修正情况 ps

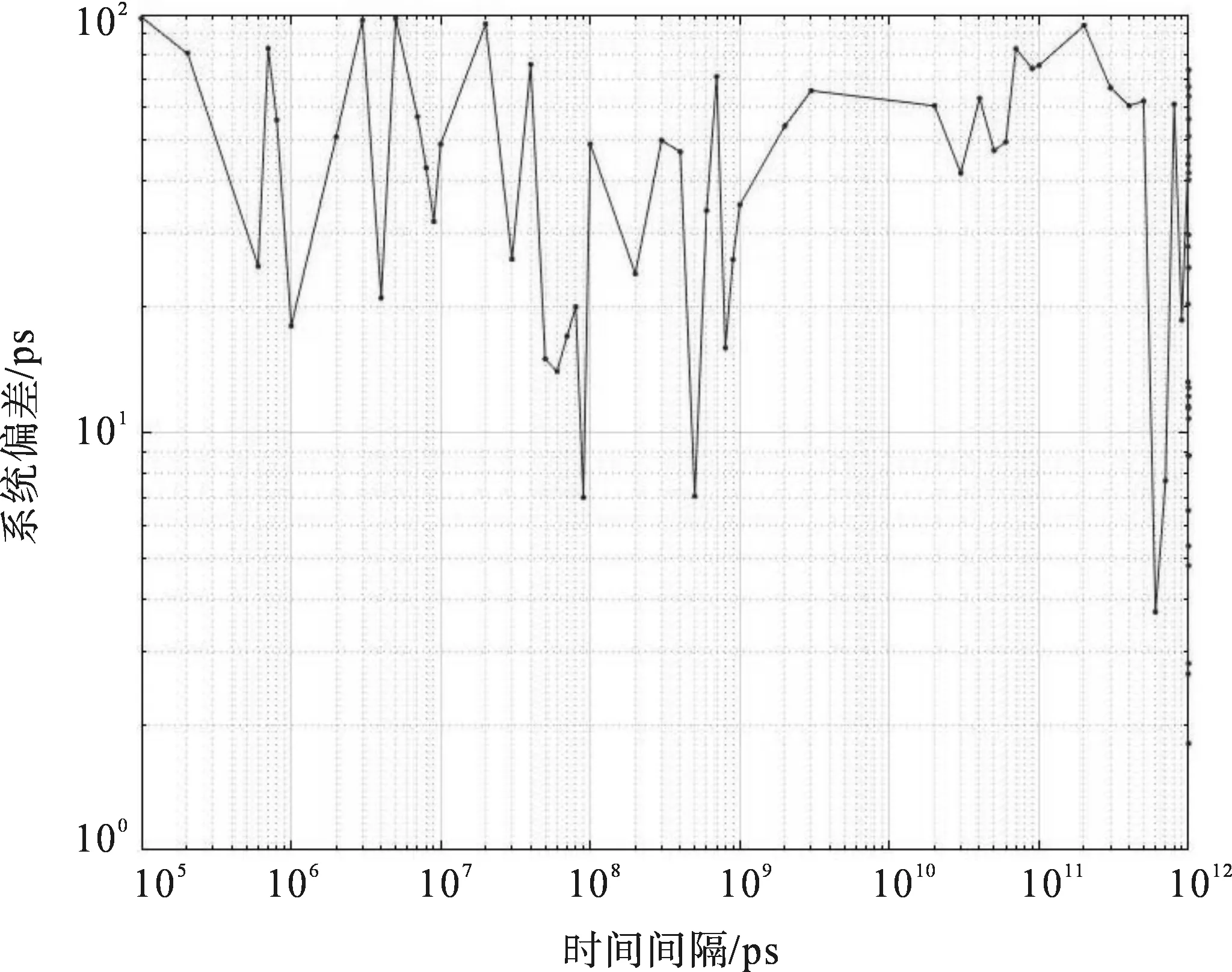
图8 整个区间内铯钟作为TDC工作时钟时的系统偏差

对于铷钟来说拟合的直线方程为y=4.78×10-10x+310，其斜率为4.78×10-10。表2为以铷钟作为TDC工作时钟时的0～1 s测量范围内不同待测时间间隔的系统偏差与修正结果的对比，可以看出，通过一次线性拟合其结果同样得到显著改善，此时系统偏差平均值为49 ps。整个区间所有测试值的系统偏差拟合后的结果如图9所示。

表2 以铷钟作为TDC工作时钟时拟合修正情况 ps

图9 整个区间内铷钟作为TDC工作时钟时的系统偏差

除此之外，另取测量区间内由小到大任意10组时间间隔进行验证，结果分别如表3及表4所示。

表3 以铯钟作为TDC工作时钟时任意间隔修正后结果 ps

表4 以铷钟作为TDC工作时钟时任意间隔修正后结果 ps

综上所述，本文所建立的一次模型可以有效的将偏差修正到100 ps以下。

5 结论

本文通过探究基于FPGA的TDC系统偏差的修正方法，对基于Cyclone IV EP4CGX150DF31C7的时间间隔测量系统在使用铯钟及铷钟为工作时钟时的不同测量结果进行了分析，根据系统在整个测量范围内的偏差呈线性化趋势，设计了一次拟合校正方法，通过不同实验对校正值进行了测量，利用校正后的计数器进行了测试实验，验证了系统偏差修正方案的正确性，使系统偏差控制在100 ps以下，在实际应用中，可将一次线性拟合模型参数写入CPU以实现系统偏差校正，提高时间间隔测量的准确度，更好地发挥芯片的性能。